基于悬链线法的张力放线连续过程计算方法及工程试验
2021-07-29秦剑刘晨齐志强乔良
秦剑,刘晨,齐志强,乔良
(1. 中国电力科学研究院有限公司,北京100055;2. 国网山东省电力公司,济南250001)
0 引言
放线施工是输电线路施工的一道重要工序,根据相关标准要求,特高压工程中均采用张力放线方式[1],使导线在施工过程中始终处于架空状态,避免导线与地面接触造成表面磨损,从而减少导线带电运行后的电晕损耗和电磁污染。因此,张力放线施工方法和工艺水平的高低对线路施工质量有着重大影响[2 - 4]。
随着电压等级的不断提高,导线截面尺寸也在不断增大,从常用的630 mm2截面导线,发展至1 660 mm2大截面导线,对张力放线施工机具的承载性能也有了更高要求。而目前张力放线计算中主要采用的斜抛物线法在大高差、大跨距等复杂地形下计算结果不够精确,在导线连接器、卡线器、滑车载荷等关键参数的计算上有一定误差,不能为施工机具的设计提供更准确的数据支持[5]。
张力放线施工作业受环境影响较大,尤其山区地形下张力场选址困难,放线区段长度可达10 km,任何一个作业点出现问题就会造成整个区段停工,对施工进度影响较大,因此放线过程中的状态分析和计算非常重要[6]。而目前采用的斜抛物线法仅对牵引板(连接牵引绳与导线)在铁塔滑车处的状态进行计算[7],无法计算牵引板在任意位置时的导线弧垂、牵引机及张力机载荷、导线对滑车的包络角等,造成放线区段的计算及监控盲区。
另外,现有施工标准DL/T 5286—2013[1]中采用的滑车综合阻力系数为滑车两侧牵引绳或导线张力的比值,忽略了滑车所受载荷对阻力的影响,与实际情况不符,当滑车较多、导线对滑车包络角较大时存在较大偏差,造成牵引力、张力计算误差。
因此,本文提出适用于输电线路张力放线连续过程分析的精确计算方法,计算了放线过程中的张力机载荷(放线张力)、牵引机载荷(牵引力)、导线过滑车支反力及包络角、导线空间坐标等变化情况,并在特高压工程中进行现场试验,验证了计算方法的准确性,为施工过程放线提供技术支撑。
1 张力放线系统
张力放线的基本程序为:导引绳展放,导引绳牵放牵引绳,牵引绳牵放导线。只有牵放导线时涉及导线质量,因此本文仅针对牵引绳牵放导线过程进行分析研究。
导线牵放包括一牵1(1根牵引绳牵放1根导线)、一牵2(1根牵引绳牵放2根导线)、一牵4(1根牵引绳牵放4根导线)等方式。
张力放线系统由牵引机、张力机、牵引绳、导线、牵引板、放线滑车(悬挂于铁塔横担下方)等组成,如图1所示。

图1 张力放线系统示意图Fig.1 Schematic diagram of tension stringing system
2 张力放线连续过程计算方法
2.1 放线参数
以张力机、牵引机、放线滑车为放线系统的节点,牵引板为移动节点。设共有n+1个节点(放线滑车n-1个),节点间相对高差为hi,i=1,…,n, 相对跨距为Li,i=1,…,n。 放线系统节点示意图如图2所示。

图2 张力放线系统节点Fig.2 Nodes of tension stringing system
2.2 张力放线系统方程
根据放线系统模型,可建立连续放线系统方程组,包括节点间高差及跨距方程、牵引板在导线及牵引绳作用下的平衡方程、导线及牵引绳在滑车前后的平衡方程及施工控制方程等。
2.2.1 节点间高差及跨距方程
在放线系统中,认为导线是从牵引板到张力机间的具有弹性的连续柔性索。当牵引板位于节点k及k+1之间时,导线被滑车节点分割为k个悬链线段。各悬链线段的高差hci及跨距Lci表达式[8 - 9]如式(1)所示。
(1)

同样,认为牵引绳是从牵引机到牵引板的连续柔性索,当牵引板位于节点k及k+1之间时,牵引绳被滑车节点分割为n-k+1个悬链线段。各悬链线段的高差hrj及跨距Lrj表达式为:
(2)

从放线施工整体系统考虑,认为在放线过程中张力机、牵引机、放线滑车各节点之间的距离始终不变,因此当牵引板位于节点k及k+1之间时,可以建立节点间的高差h及跨距L方程如式(3)—(4)所示。
(3)
(4)
2.2.2 牵引板平衡方程
当牵引板位于节点k及k+1之间时,认为牵引板在导线、牵引绳及重力的作用下保持平衡。牵引板(一牵2)示意图如图3所示,牵引板所受载荷如图4所示。
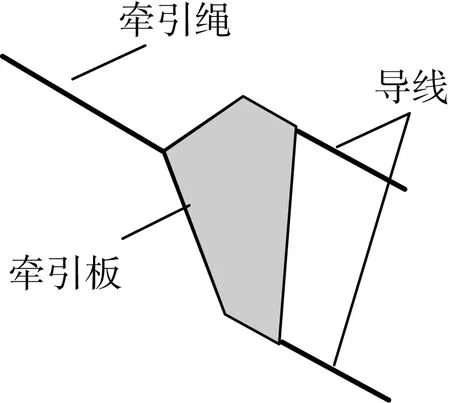
图3 一牵2的牵引板示意图Fig.3 Schematic diagram of one pulls two traction board
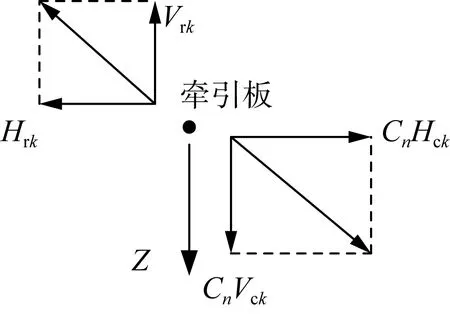
图4 牵引板所受载荷Fig.4 Load on the traction board
因此当牵引板位于节点k及k+1之间时,垂直方向的平衡方程为:
(5)

水平方向所受载荷包括导线、牵引绳对牵引板的水平力,因此水平方向的平衡方程为:
Hrk=CnHck
(6)
2.2.3 滑车前后平衡方程
通过滑车的导线、牵引绳受到的滑车摩阻力的作用,导线通过滑车节点i+1时的载荷示意图如图5所示。

图5 导线对滑车节点的载荷Fig.5 Load of pulley node by conductor
因此,当牵引板位于节点k及k+1之间时,导线、牵引绳受滑车摩阻力的方程为:
(7)

另外,导线、牵引绳对滑车的包络角β表达式分别为:
(8)
(9)
2.2.4 施工控制方程
连续张力放线施工过程中,需要根据现场条件在不同时间对放线系统进行作业控制。控制方式主要为牵引力控制、张力控制(为保证系统的平衡稳定,2种控制方式不能同时采用)。
(1)当需要保持稳定的张力机出口张力时,采用张力控制。建立张力控制方程如式(10)所示。
(10)
式中T张为给定的张力机出口张力,N。
(2)当需要增加牵引机牵引力时,采用牵引力控制。建立牵引力控制方程如式(11)所示。
(11)
式中T牵为给定的牵引机出口牵引力,N。
另外在施工中可控制牵引板的位置,因此建立牵引板行进控制方程如式(12)所示。
(12)
式中L牵为张力机到牵引板的水平距离,m。
2.2.5 放线系统方程组
以上节点间高差及跨距方程、牵引板平衡方程、滑车前后平衡方程及控制方程可以构成闭合的非线性方程组,共包括3n+3个方程,待定未知数为Sci、Hci、Vci(i=1, …,k),Srj、Hrj、Vrj(j=k, …,n)。
2.3 放线过程连续迭代
以张力机到牵引板的水平距离L牵作为连续放线的过程参数。在放线开始时,L牵为0,按无导线情况下的非线性方程组计算获得Srj、Hrj、Vrj等初始结果。
改变牵引绳水平位置L牵,以初始结果作为上一状态结果,按当前的牵引绳及导线长度对上一状态结果进行分解,作为在当前控制条件下构成的非线性方程组迭代初值,计算当前状态下各节点间牵引绳、导线的长度、水平张力、节点垂直力。该迭代方法能保证非线性方程组的收敛性。
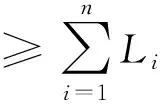
通过连续计算即可得到牵引力、放线张力、各滑车节点上滑车包络角及载荷等参数随牵引板行进的变化过程。并根据悬链线方程[10 - 11]可以得到放线过程中任意点处牵引绳、导线的空间位置。
3 现场放线工程试验
为深入研究放线施工过程中放线滑车受力、观测档弧垂等参数变化,验证连续张力放线计算方法,在青海-河南±800 kV特高压直流工程某标段开展了现场放线工程试验。测量放线过程中放线滑车所受载荷、观测档导线弧垂等数据,并与计算结果进行对比分析。
3.1 放线试验布置
3.1.1 放线区段及设备安装
放线区段为N4911—N4920,区段最大高差为111 m、最大跨距为1 026 m。。
放线工程试验示意图如图6所示,将无线力传感器连接在5号(N4915)、7号(N4917)、8号(双滑车)(N4918)放线滑车上,串联方式如图7所示。试验时在塔位下方附近设置数据采集点,由便携式计算机读取无线力传感器实时数据。
3.1.2 放线施工参数
采用同极导线3×(一牵2)同步展放方式,以公称方径28 mm的防扭钢丝绳作为牵引绳,通过牵引板牵引1 250 mm2大截面导线。

1-张力机;2-牵引机;3-塔架;4-放线滑车;5-无线力 传感器;6-导线图6 放线工程试验示意图Fig.6 Schematic diagram of tension stringing engineering test
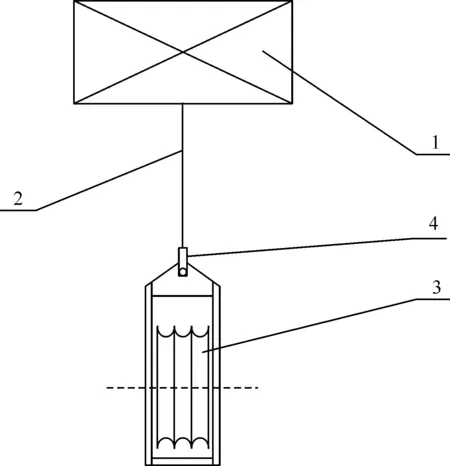
1-横担;2-挂具;3-放线滑车;4-无线力传感器图7 无线力传感器连接Fig.7 Connection of wireless tension sensor
导线抗拉刚度EEAc=25 090 kN,导线单位重力qc=41.67 N/m;牵引板重力Z=1 086.82 N;牵引绳抗拉刚度EEAR=25 434 kN,牵引绳单位重力qr=28.22 N/m。
试验时张力机初始控制张力值设定为25 kN,在导线通过5号滑车后,为调整导线弧垂,增大张力机张力至40 kN。
在此认为各滑车轴摩擦系数相同,均为0.08[12]。
3.2 试验数据测量及数据对比
3.2.1 放线滑车载荷
1)数据测量
在牵引板分别通过1—10号放线滑车后,待牵引板及导线完全静止,每隔10 s读取并记录5号、7号、8号放线滑车的载荷数据,共读取3次,以3次测量数据的平均值作为滑车载荷。
2)数据对比
牵引板分别通过1—10号放线滑车时5号、7号、8号滑车载荷与计算数据的对比分别如图8—10所示,图中横坐标为滑车编号,纵坐标(左)为滑车载荷,纵坐标(右)为滑车测量数据与计算数据间相对偏差。
从图8可以看出,牵引板在通过5号滑车前,载荷最大偏差(绝对值)为2.22 kN,相对偏差13.50%;通过5号滑车后,载荷最大偏差为2.00 kN,相对偏差3.27%;平均相对偏差绝对值为5.02%。

图8 试验与计算载荷数据对比(5号滑车)Fig.8 Comparison of test data and calculation data of load (No.5 pulley)
从图9可以看出,牵引板在通过7号滑车前,载荷最大偏差(绝对值)为2.59 kN,相对偏差6.26%;在通过7号滑车时,偏差值达到最大,4.04 kN,相对偏差6.97%;通过7号滑车后,载荷最大偏差为1.15 kN,相对偏差1.85%;平均相对偏差绝对值为3.43%。
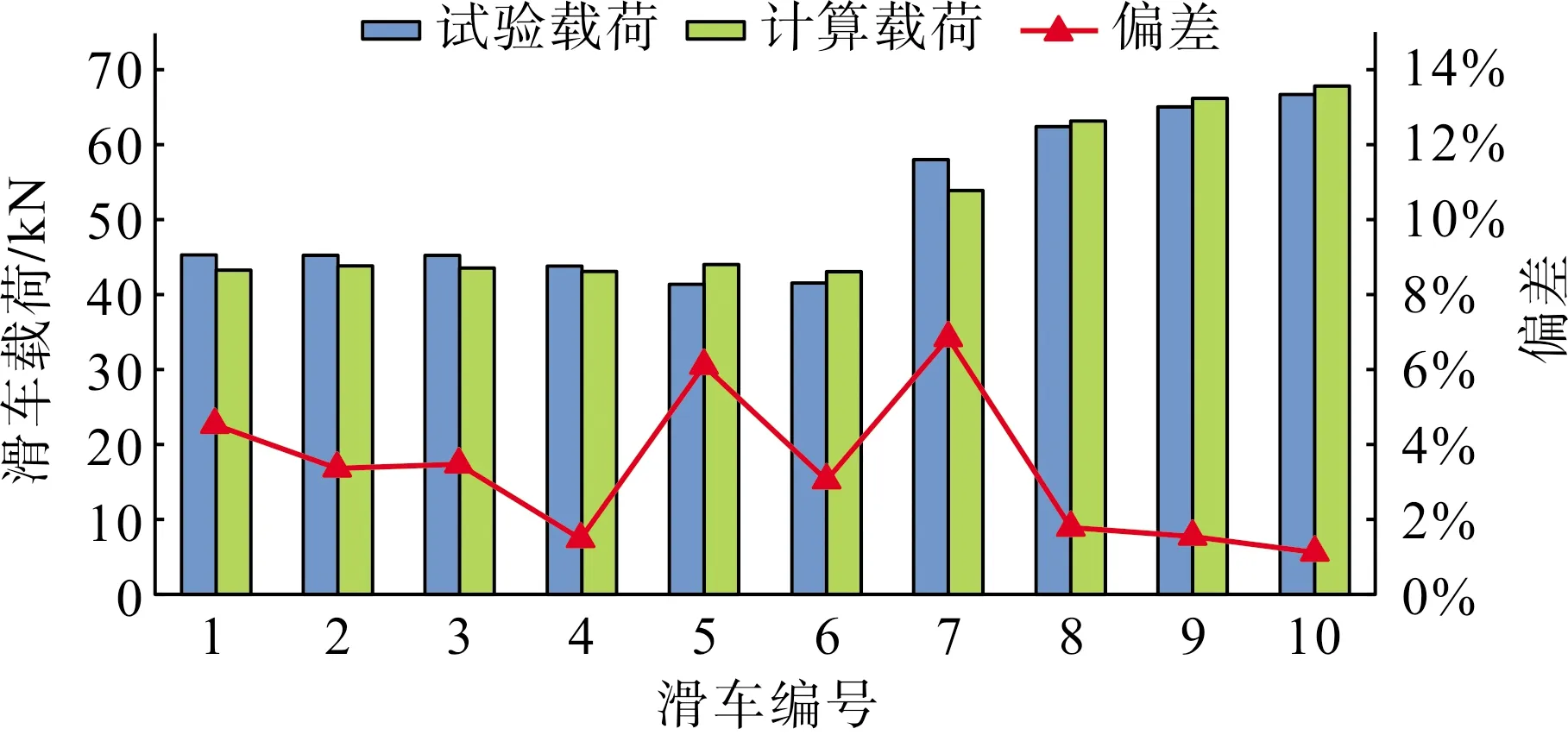
图9 试验与计算载荷数据对比图(7号滑车)Fig.9 Comparison of test data and calculation data of load (No.7 pulley)
从图10可以看出,牵引板在通过8号滑车前,载荷最大偏差(绝对值)为2.64 kN,相对偏差9.31%;在通过8号滑车时,偏差值达到最大,4.01 kN,相对偏差11.02%;通过8号滑车后,载荷最大偏差为0.24 kN,相对偏差0.60%;平均相对偏差绝对值为5.07%。

图10 试验与计算载荷数据对比图(8号滑车)Fig.10 Comparison of test data and calculation data of load (No.8 pulley)
3)偏差原因分析
(1)工程中各滑车的实际摩阻系数有变化,造成滑车载荷测量数据与计算数据的偏差;
(2)无线力传感器在铁塔上长时间悬挂,受气温、湿度变化影响,测量数据有一定误差;
(3)对于双滑车,因无线力传感器安装在靠近牵引侧的滑车上,安装位置不完全水平,造成双滑车中前后滑车间存在高度差,如图11所示,造成测量数据与计算数据的偏差。

图11 双滑车悬挂Fig.11 Suspension double pulley
在后续试验测量中可以采用以下2条措施减少测量数据偏差。
(1)施工放线前应对牵引机、张力机力值进行标定并进行修正,以减小牵张设备显示力值对放线参数计算结果影响;
(2)针对双滑车结构,增加载荷数据测量点,获得更精确载荷测量结果。
3.2.2 牵引板通过每个滑车后指定观测档弧垂
1)数据测量
在牵引板分别通过1—10号放线滑车后,待牵引板及导线完全静止,使用全站仪测量N4918—N4919、N4919—N4920线档弧垂,记录试验数据。
2)数据对比
弧垂测量受观测点位置、观测人员测量误差影响较大,测量数据有一定波动。
如图12所示,牵引板通过每个滑车后N4918—N4919弧垂测量数据与计算数据变化趋势相同,平均相对偏差绝对值为8.69%。

图12 试验与计算观测档弧垂数据对比(N4918—N4919)Fig.12 Comparison of test data and calculation data of observation span sag (N4918—N4919)
如图13所示,牵引板通过每个滑车后N4919—N4920弧垂测量数据与计算数据变化趋势相同,平均相对偏差绝对值为7.65%。

图13 试验与计算观测档弧垂数据对比(N4919—N4920)Fig.13 Comparison of test data and calculation data of observation span sag (N4919—N4920)
3.3 试验对比分析
通过以上试验测量数据与计算数据的对比可以看出,滑车的载荷数据相对偏差在6%以下,观测档弧垂相对偏差在9%以下,验证了计算方法的准确性,数据精度满足工程需求。
4 结论
本文在分段悬链线理论的基础上提出了张力放线连续过程计算方法,实现了牵引板从张力机运行到牵引机全过程的放线状态计算,可精确计算不同规格型号的导线及牵引绳的张力及坐标、滑车包络角及载荷等参数的空间及时间连续数据,方法可应用于一牵1、一牵2、一牵4等不同放线方式。
通过青海-河南±800 kV特高压直流工程现场放线工程试验,对放线过程中放线滑车所受载荷、观测档导线弧垂等进行测量,并与计算结果进行了对比。计算结果与实际测量结果较为吻合,滑车的有效受力数据相对偏差在6%以下,观测档弧垂相对偏差在9%以下,验证了计算方法的准确性。
张力放线连续过程计算方法可按施工需要采用牵引力控制、张力控制等不同方式实现张力放线连续过程分析,计算精度满足工程需求,为放线过程中施工分析提供了便捷工具。
