ANPC光伏逆变器的并网研究

2021-07-29吴振鑫常国祥

电力学报 2021年2期

吴振鑫，常国祥

（黑龙江科技大学电气与控制工程学院，哈尔滨 150022）

0 引言

随着光伏产业的蓬勃发展，电网对光伏并网逆变器提出了更高的要求，对所并电能的质量要求也越来越严格。故将三电平逆变器应用在光伏逆变系统中，并采用高效的逆变策略和并网控制策略有着重大的现实意义。

文献［1］提出了采用新型的三电平NPC拓扑结构并结合VFOC的控制策略作光伏逆变器。这种逆变结构和控制策略可以很好地提高逆变效率且可以很好地解决中点平衡问题，但是逆变效果会受到LCL滤波器的影响。谐振的产生是由系统整体的阻尼太小造成的，增加系统的阻尼可采用有源阻尼法或无源阻尼法。无源阻尼不仅影响滤波效果而且会增加额外的损耗，而有源阻尼是通过算法来增加阻尼的，不存在上面的问题，所以被广泛接受和利用［2-4］。文献［5］对几种虚拟电阻法进行了比较，但是受控制宽带及控制器结构的限制，这几种方法的效果均不太理想。应用状态反馈可以对闭环控制系统进行任意极点的配置，如线性二次型（LQ）法［6］、直接极点配置法［7］等，但其性能好坏在很大程度取决于设计者的经验。文献［8］提出了构造一个具有负谐振峰值来抵消正谐振峰值的方法，这种方法不仅容易理解且构造方便，对系统的低频和高频特性均无影响。

文献［9］提出了采用ANF（自适应陷波器）与PNSC（正负序消除计算）结合的方法实现正负序分离，在两相静止坐标系下完成锁相。实验结果表明，该方法在奇次谐波下仍可以快速地实现锁相，但是没有考虑直流分量对PLL的影响。文献［10-11］在SOGI-PLL的基础上进行了改进，有效地消除了直流分量对锁相的影响，并在此基础上提出了滑动平均滤波的原理（MAF）并对奇次谐波进行消除，然后通过在提取电网电压中的正序分量的方式来实现锁相。实验表明，该方法的锁相效果良好，能提高锁相的速度与精度，但使用MAF算法时计算量较大，使PLL的响应时间变长，影响PLL的动态性能。

本文以ANPC为硬件平台，在VFOC控制策略的基础上引入电容电流构成具有负谐振峰值的陷波器来减弱LCL滤波器产生正谐振峰值对系统的影响，并在SOGI-QSG的基础上提出了改进的PLL，在传统的SOGI基础上加入FLL（锁频环）和直流消除器，使其不仅能消除直流分量对锁相的影响，而且当电网频率出现微小波动时可以快速实现锁相，具有频率自适应能力，提高了PLL的动态性能和鲁棒性。通过在Simulink中搭建仿真平台，验证所提系统的可行性。

1 硬件电路图

1.1 ANPC光伏逆变器的结构框图

DC直流电源通过ANPC光伏逆变器后变为交流，然后通过锁相环实现与电网的并列运行。为了使逆变出来的交流量更加平滑，ANPC光伏逆变器内置了LCL滤波电路。为了降低开关管的损耗和改善逆变波形，ANPC光伏逆变器采用了三电平SVPWM的控制策略。

以电网电流为反馈量的闭环控制采用VFOC的控制策略，本次研究在此基础上引入电容电流，构造出一个具有负谐振峰值的传递函数，来抵消LCL滤波电路产生的正谐振峰值。锁相环在传统SOGI-QSG的基础上也进行了改进，引入了直流消除器和FLL（锁频环），使其不仅能消除直流分量对锁相的影响，而且当电网频率出现微小波动时可以快速实现锁相，具有频率自适应能力。其具体结构框图如图1所示。

图1 ANPC光伏逆变器的结构框图Fig.1 Structure block diagram of ANPC photovoltaic inverter

1.2 ANPC三电平逆变拓扑

ANPC三电平逆变器电路拓扑如图2所示。直流侧电源用DC1、DC2来表示，Sa1—Sa6、Sb1—Sb6、Sc1—Sc6为桥臂开关管IGBT和其两端反并联二极管的组合，可见每个桥臂有4个开关，并且中间两个开关管又跨接两个二极管；Ua、Ub、Uc分别是逆变侧的三相电压；L1a、L1b、L1c是逆变侧的滤波电感；L2a、L2b、L2c是电网侧的滤波电感；Ca、Cb、Cc是电网侧的滤波电容和等效电容之和；IL1、IC、IL2分别表示通过逆变侧电感的电流，通过滤波电容的电流，通过网侧电感的电流；Uga、Ugb、Ugc分别是电网的三相电压；O点表示三电平的中点电位；Ng为电网的中性点；N为三相滤波电容的中性点。

图2 ANPC三电平逆变器的硬件图Fig.2 Hardware diagram of ANPC three level inverter

2 控制策略的研究

2.1 VFOC

网侧电流由三相静止变为两相静止（Clack变换），如式（1）所示，其中Tc是其对应的变换矩阵，具体参数如式（2）所示；再由两相静止变为两相旋转（Park变换），如式（3）所示，其中Tp是其对应的变换矩阵，具体参数如式（4）所示；经过解耦，并且与给定电流参考值比较后，所产生的差值通过PI控制器来实现对并网电流的控制，在经过反Park变换后通过SVPWM控制策略达到控制开关管的目的。

在虚拟磁链定向的同步旋转坐标系中，由图2可知有eq=|E|，ed=0，将其带入瞬时功率理论公式（式（5））可得式（6），式中q表示无功功率，p表示有功功率。

由上述算式可知，有功功率与无功功率只与并网逆变器输出电流在d、q轴分量上的id、iq成正比。假设变换前后无功率损失，则有公式（7）成立。

2.2 陷波器的构造

LCL型滤波会产生一个正谐振峰值，通过构造一个负谐振峰作为负反馈，以此来消除LCL滤波器产生的正谐振峰值。构造的陷波器如图3所示。

图3 陷波器结构有源阻尼算法结构简图Fig.3 Structure diagram of active damping algorithm for notch filter structure

图3中E(s)为逆变器侧输出电压到所选的反馈变量处的传递函数；K(s)为选取不同反馈量时配置的传递函数；C(s)为并网电流调节器的传递函数；D(s)为构造的陷波器传递函数，如式（8）所示，其中Q为陷波器的品质因素。

在电流前向通路中引入反馈量，使其与该电流环的前向通路构成闭环系统，将其配置成陷波器的特性，从而实现对LCL并网逆变器的有源阻尼控制。但是选取反馈量的不同会使系统在配置陷波器的传递函数时存在差异。就LCL型并网逆变器而言，在电网侧电流为主回路的情况下，反馈量的选择可以有以下5种方案：电网侧电感电压U2；滤波侧电容电压Uc；滤波侧电容电流Ic；逆变器侧电感电压U1；逆变器侧电感电流I1。当选取滤波侧电容电流为反馈量时，只需要将陷波器中的K(s)配置成比例环节即可；当选取电网侧电感电压和滤波侧电容电压作为反馈变量时，需要将陷波器中的K(s)配置成微分环节；当选取逆变器侧电感电压与逆变器侧电感电流当反馈时，在配置K(s)将更为复杂。所以本文选取了实现起来较容易，而且不受系统其它参数影响的滤波侧电容电流作为反馈量。式（9）为选取不同反馈量时的E(s)配置情况，式（10）是带入具体系统参数值后E(s)和其对应的K(s)的配置情况［12］。

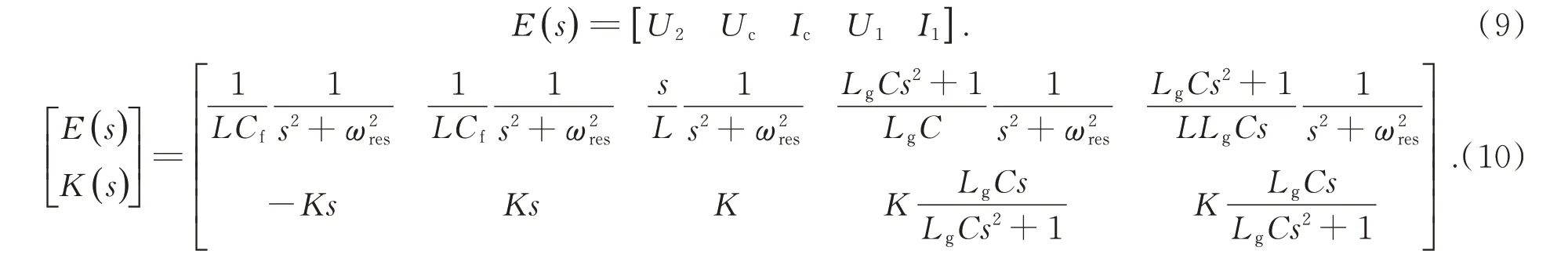
3 改进型锁相环

改进SOGI-QSG是在SOGI-QSG的基础上增加了一个积分器，并对其进行适当的放大。新增积分器的输出电压与传统SOGI-QSG的输出电压U′相加之后作为反馈信号，与SOGI-QSG的输入电压做差，从而消除直流分量对锁相的影响。

当电网频率发生波动时，为了实现频率自适应，在改进型SOGI-QSG的基础上加入了锁频器（FLL）和直流消除器，则改进SOGI-QSG后的PLL结构框图如图4所示。即把q U′与电压误差ΔU相乘后，通过FLL的负反馈系数－γ进行在线调节，然后对其积分后作为改进型SOGI-QSG的频率使用。当电网频率发生微小波动时（即ω≠ω0时），通过不断调节可以减少ω与ω0之间的误差，使误差频率ɛf逐渐趋于零，从而达到频率自适应的目的，使其输出频率ω0更加接近电网频率ω，从而提高了PLL的动态性能和鲁棒性能［13-15］。图4中x1、x2、x3是中间变量；K1表示直流消除器的比例系数，取K1=0.25；K=1.414。

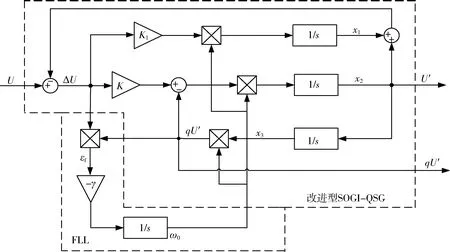
图4 有频率自适应的改进型SOGI-QSG结构框图Fig.4 Structure diagram of improved SOGI-QSG with frequency adaptation

由图4可以列出式（11）与式（12）所示的改进SOGI-QSG后PLL的状态空间表达式，其中ω˙0、x˙1、x˙2、x˙3分别为ω0、x1、x2、x3的状态变量。

当ω≠ω0时，由图4可得电压误差ΔU为式（14），频率误差εf为式（15），可以通过在线调节－γ使其逐渐满足εf=0，从而使ω=ω0，进而达到频率自适应的目的。

当系统趋于稳定时，则有ΔU=0，即U=x1+x2，则式（11）可转化为式（16）：

式（16）的特征根为λ=±jω0和λ=0，所以系统稳态响应以ω0等幅震荡。当输入信号是U=UNsin(ωt+φ)，由SOGI-QSG的基本原理得系统的稳态响应如式（17）所示，可知改进型SOGI-QSG能准确检测和跟踪电网电压的频率。

当有频率自适应的改进型SOGI-QSG处于稳态时，近似视ω=ω0，则有ω20－ω2=2ω0(ω0－ω)，则式（12）可以化解为式（18）：

设误差信号σ=ω0－ω，作为频率自适应环的梯度变化，因ω为系统输入频率，其可视为常数，则σ的一阶导数σ˙=ω˙0。设李雅普诺夫能量函数为式（19），可见其是正定的，对式（19）进行求导可得式（20），可见其是负定的，根据现代控制理论中李雅普诺夫第二法，可以判定该系统是渐进稳定的。

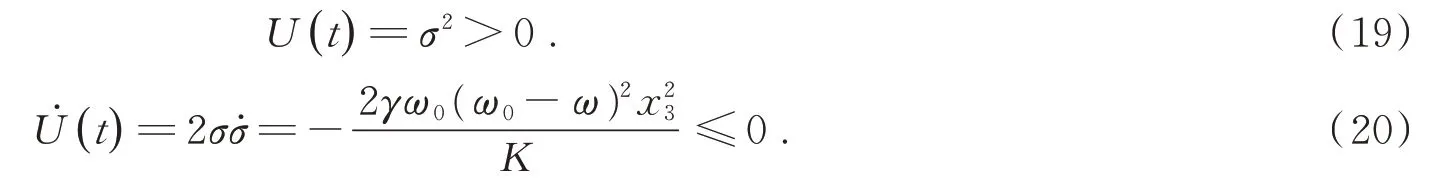
4 系统参数

为了尽可能地减少无功功率，在选择电容大小时，一般限制其产生的无功功率小于系统额定功率的5%，则其应该满足式（21），其中Pn为并网逆变器额定功率，Uc为滤波电容电压，Un为并网逆变器额定电压，且有Uc=Un。

从稳态条件下并网逆变器输出功率的能力考虑，对并网逆变器LCL滤波器的总电感量应给予合理的限制。若采用SVPWM控制策略，其应该满足式（22），其中EP为网侧电压的峰值；ILP为滤波电流的峰值；Udc为直流侧电压。

文章首先确定的是逆变桥侧的电感值。为尽可能地降低开关损耗，保证开关管在承受的开关应力范围内，需要考虑逆变桥侧电流纹波对电感选择的影响。逆变器侧的电感值与最大电流纹波幅值应满足式（23），其中Δi为最大电流纹波幅值。

在初选并网逆变桥侧的电感后，可由式（22）和式（24）—式（28）确定网侧电感值。

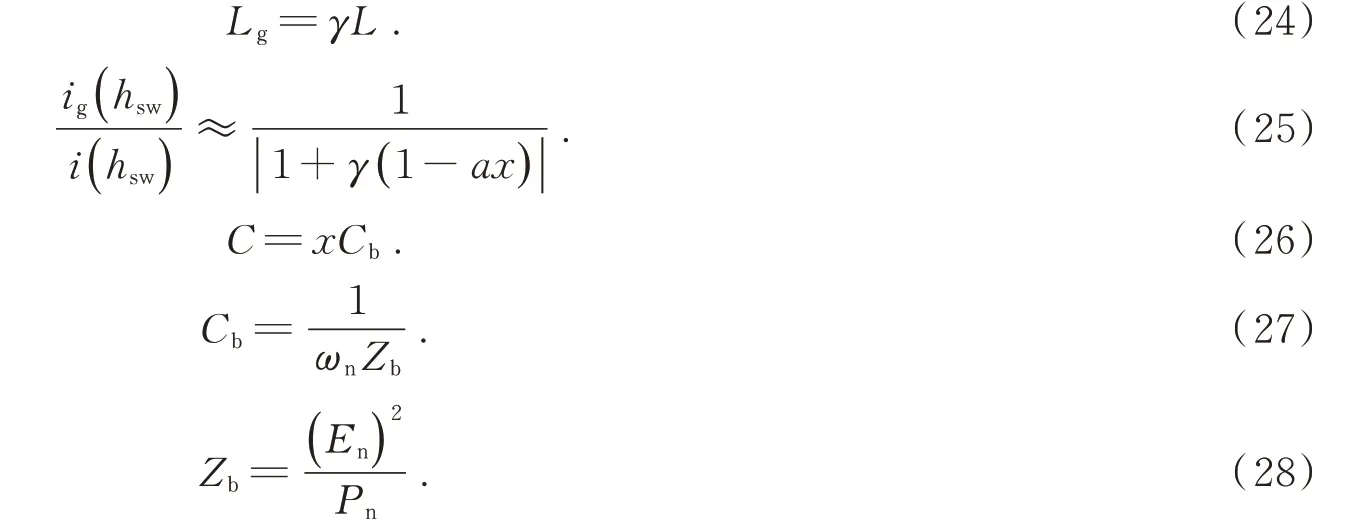
式中：hsw=ωsw/ωn，为开关谐波次数，一般约为20%；ωsw为开关角频率；γ为网侧电感与逆变桥侧电感值之比；x为滤波电容吸收系统功率中无功功率的百分比，且有x≪5%；Cb为电容单位值。

本文中的谐振频率设计应满足式（29），系统的具体参数见表1所示。

表1 具体参数配置Tab.1 Specific parameter configuration

5 系统仿真

图5为系统加入陷波器前后的Bode图对比情况。通过对这三种情况的Bode图作对比，可以很清楚地看出陷波器的谐振与LCL滤波器产生的谐振相位相同幅值相反，加入陷波器后的LCL型逆变器无谐振峰值；系统低频和高频开环增益受到陷波器的影响可以忽略不计，说明陷波器的引入并没有破坏LCL滤波环节对高频信号的抑制；从相位图中可见，原系统中由LCL环节引入的共轭极点所引发的谐振频率处180°相位突变也得到了改善。

图5 加入陷波器前后的系统Bode图Fig.5 Bode diagram of the system before and after adding the notch filter

对加入陷波器后并引入Ic作为反馈量的VFOC控制策略的稳定性能进行了验证分析，图6是加入陷波器后的零极点图，由图可知没有陷波器时，一对共轭主导极点位于虚轴右半平面，此时系统不稳定；而加入陷波器后，陷波器引入的一对零点与原系统中不稳定的主导极点构成一对偶极子，从而消除了系统的不稳定性，而新引进的一对极点在负实轴区域且离虚轴较远，所以对系统的性能没有太大的影响。

图6 加入陷波器后的零极点图Fig.6 Pole zero graph with notch filter

图7为在Simulink中搭建的10 kW并网逆变系统的仿真图。图8为未加入陷波器时，并网系统在Simulink中的仿真波形；图9为加入陷波器后，并以Ic作为反馈量的VFOC控制策略下的并网系统的仿真波形。对比图8和图9可知，在加入陷波器并以Ic作为反馈量的VFOC控制策略下的并网电流更加平滑，波形的正弦效果更好且没有谐振发生，提高了系统的鲁棒性和稳定性。

图7 10 k W并网逆变系统仿真图Fig.7 Simulation diagram of 10 k W grid connected inverter system

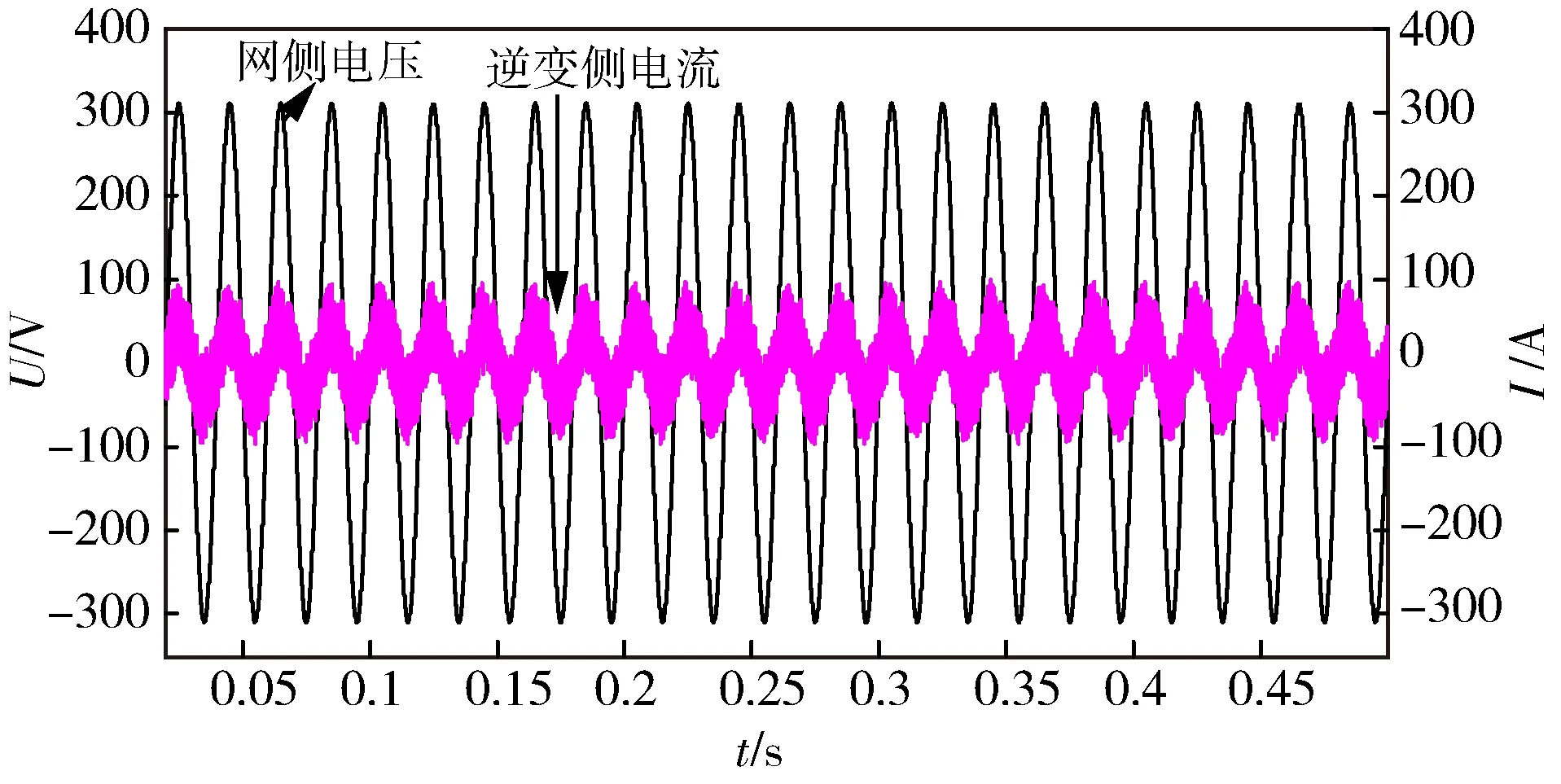
图8 加入陷波器前的并网波形图Fig.8 Grid connected waveform before adding a notch filter

图9 加入陷波器后的并网波形图Fig.9 Grid connected waveform after adding a notch filter

当三相电压中混有20 V直流分量时，改进SOGI-QSG后的输出情况如图10所示。其中图10（a）为三相电压，图10（b）为其输出频率，图10（c）为其输出相位。由图10（a）可知，直流分量使三相电压的幅值由原来的311 V变为现在的330 V；由图10（b）可知，该锁相环能在0.1 s内实现对频率的调整，从而实现对系统频率的准确跟踪；由图10（c）可知，该锁相环能够输出相位，从而实现准确的锁相。可见基于改进SOGIQSG的频率自适应锁相环能够滤除直流分量对系统的影响，快速地实现频率跟踪，并准确地进行锁相。

图10 混有直流分量下基于改进SOGI-QSG的频率自适应锁相环的输出情况Fig.10 Output of frequency adaptive PLL based on improved SOGI-QSG under mixed DC

电网电压以工频50 Hz运行，0.1～0.3 s期间频率阶跃变化为50.1 Hz，0.3 s后恢复为工频运行。图11为频率突变情况下，DSOGI-PLL与基于改进SOGI-QSG的频率自适应锁相环的锁相对比情况。其中图11（a）为DSOGI-PLL的输出频率，图11（b）为基于改进SOGI-QSG的频率自适应锁相环的输出频率。通过对比发现图11（b）在频率发生变化时，能够快速地实现频率跟踪，说明该锁相环有更好的频率自适应功能。