气弹簧助力式四连杆铰链发动机罩的计算与优化分析

侯林 史承婕 王鹏 王海歌

（一汽奔腾轿车有限公司奔腾开发院，长春 130012）

1 前言

气弹簧助力式四连杆铰链发动机罩系统早期在轿车上较少应用。此种发动机罩可以实现更复杂的运动轨迹，造型上可以突破现有定轴铰链式发动机罩的一些限制，随着汽车造型的不断丰富，此类发动机罩应用日益广泛。随着需求的增加，对此种发动机罩系统的应用研究也提出了更高的要求。

目前，关于气弹簧助力式机构的研究主要分为2个方向：一是定轴铰链机构，结构简单、普遍应用于尾门，这方面理论计算分析成果丰富[1-6]；二是四连杆机构，结构复杂，一般应用于发动机罩或行李箱上，这方面计算分析成果相对较少[7-8]。本文借鉴上述2 方向的研究成果，细化气弹簧助力式四连杆机构的理论分析和验证过程，并给出开闭操作力等参数优化方向，为后续布置参数自动优化提供参考。

2 发动机罩四连杆铰链的机构布置与设计

2.1 机构布置

发动机罩四连杆铰链的布置需要综合考虑运动校核、刚度性能、空间利用和外观等多方面的要求，主要体现在2个方面：

a.四连杆铰链的布置位置与定轴铰链布置类似，需要尽量增大在整车Y向上的尺寸，以利于保证发动机罩获得更大的整体刚度，并尽量在整车X向上靠近车后方向，以利于发动机罩运动校核。

b.固定方式主要有2种，即水平安装、整车Z向固定和侧向安装、Y向固定。前者的优点是铰链处无需遮蔽，车身侧无孔洞，缺点是铰链Z向不可调，易造成发动机罩间隙段差不良；后者如图1 所示，优点是铰链Z向可调，方便调整发动机罩的间隙段差，缺点是铰链处难以遮蔽，车身侧存在孔洞。

图1 气弹簧助力式四连杆铰链开启机构

2.2 机构设计

机构设计主要应满足发动机罩的运动轨迹要求，具体包括：

a.四连杆长度的设计，主要通过CATIA 软件，应用作图解析法进行。

b.四连杆铰链的瞬心设计，图2 所示为某车型开发完成后四连杆铰链的瞬心轨迹，发动机罩X向坐标最大值需保证在瞬心轨迹内侧，这主要是为了保证发动机罩后点的运动轨迹向上。

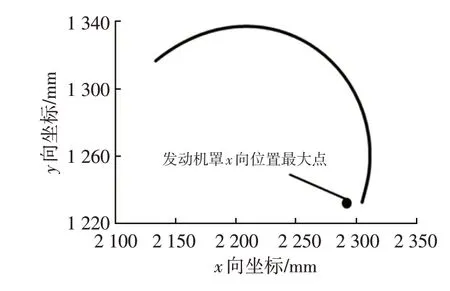
图2 四连杆铰链瞬心轨迹示意

3 发动机罩开闭操作力分析

3.1 发动机罩的力学分析模型

图3 所示为某车型的发动机罩受力分析模型，其中，A、B、C、D为四连杆铰链的4 个旋转轴心，S1、S2为气弹簧的固定点，T为铰链机构的瞬心，H为开、闭发动机罩的操作点，在ZX平面内进行发动机罩开启和关闭过程中的操作力分析。

图3 发动机罩力学分析模型

发动机罩开启过程中：

式中，MG为发动机罩重力矩；Mh为铰链阻力矩；MO为发动机罩开启操作力力矩；MS为气弹簧力矩。

则：

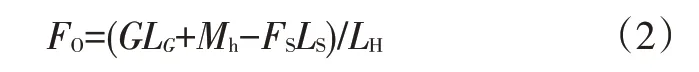
式中，FO为发动机罩开启操作力；G、LG分别为发动机罩重力及其力臂；FS、LS分别为气弹簧输出力及其力臂；LH为发动机罩开闭力臂。

发动机罩关闭过程中：

式中，MC为发动机罩关闭操作力力矩。

则：

式中，FC为发动机罩关闭操作力。

为了计算发动机罩的开闭操作力，需要先求解发动机罩的旋转中心T（瞬心）的位置，再由此计算MG、MS等相关力矩。

3.2 四连杆机构的运动求解

为了求解四连杆机构的瞬心位置，需要对四连杆机构的各运动参数进行求解。如图4所示，已知四连杆机构的各初始角度分别为Φ1、Φ2、Φ3、Φ4，各连杆长度分别为LAB、LBC、LCD、LAD，需求解发动机罩在开闭运动过程中四连杆内部角度变化情况。取Φ1为角度自变量，则机构内其他角度为：

图4 四连杆机构运动分析模型

则Φ4=2π-Φ1-Φ2-Φ3。

3.3 四连杆铰链的瞬心坐标计算

瞬心位置的计算可以根据文献[9]确定，对于图4中的T点位置，设其坐标为(XT,ZT)，则：

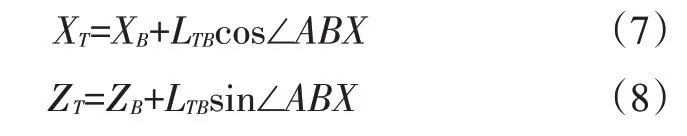
式中，(XB,ZB)为铰链的旋转轴心B的坐标；LTB=LTA+LAB为瞬心T与旋转轴心B的距离；LTA=LADsin(π-Φ1)/sin(π-Φ3-Φ4)为瞬心T与旋转轴心A的距离；∠ABX=arctan[(ZC-ZB)/(XC-XB)]+Φ3；(XC,ZC)为铰链的旋转轴心C点坐标。

3.4 重力矩的计算

图5 所示为重力矩分析模型，先求取质心点坐标，然后求取重力臂，最后求取重力矩。设质心O点坐标为(XO,ZO)，旋转轴心A点坐标为(XA,ZA)，则：

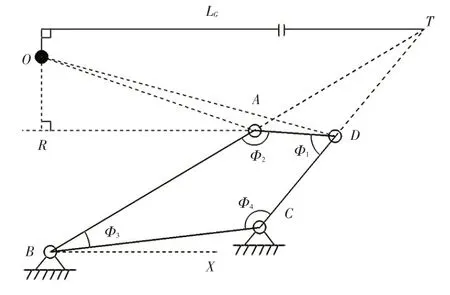
图5 重力矩分析模型

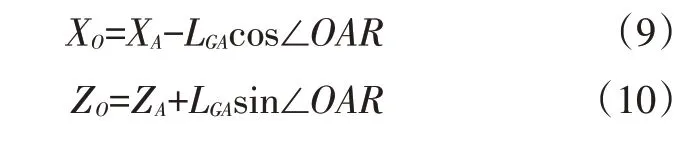
式中，XA=XB+LABcos∠ABX；ZA=ZB+LABsin∠ABX；LGA为质心O与旋转轴心A的距离；∠OAR=2π-∠OAD-Φ2-∠ABX；；LGD为质心O与旋转轴心D的距离。

根据以上参数可求得重力臂LG=XT-XO，重力矩MG=G(XT-XO)。

3.5 气弹簧力矩的计算

3.5.1 气弹簧力臂的计算

图6 所示为气弹簧力臂分析模型。气弹簧力臂LS=LS2Tsin∠S1S2T，LS2T为气弹簧发动机罩固定点与瞬心间的距离。参考发动机罩质心坐标的推导过程，可得到发动机罩任意开度下的气弹簧安装点坐标S2(XS2,ZS2)。则：

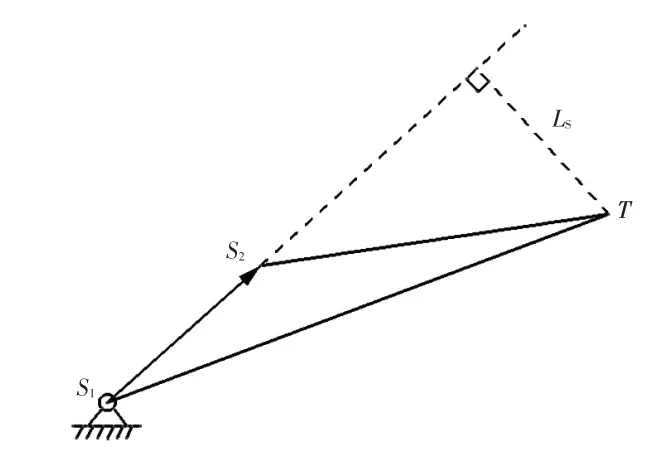
图6 气弹簧力臂分析模型

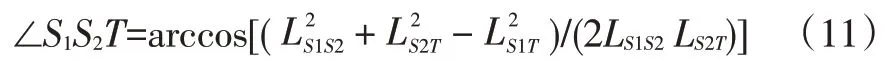
式中，LS1S2为气弹簧固定点间的距离；LS1T为气弹簧车身固定点与瞬心之间的距离。

3.5.2 气弹簧输出力的计算

气弹簧的反力特性如图7所示，图中F1、F2、F3、F4为气弹簧特性力，Le为气弹簧行程，C1、C2分别为测力点。在确定气弹簧输出力时，首先要确定系统所需的最小气弹簧力，然后根据气弹簧的输出力特性，求得发动机罩在开、闭过程中气弹簧的力矩MS。

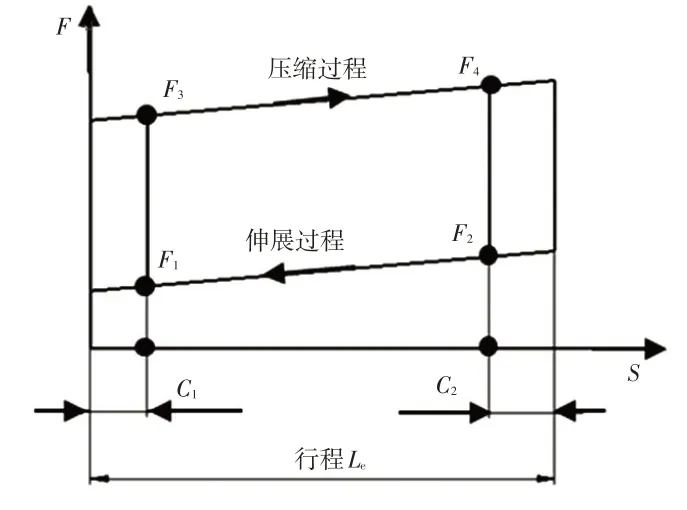
图7 气弹簧输出力特性

3.5.2.1 气弹簧输出力最小值的确定

发动机罩开闭操作力在高温、常温和低温条件下具有不同的工程目标要求。首要是保证发动机罩在极端低温环境下（-30 ℃）不会掉落伤人，所以将该工作条件下气弹簧设计需要满足的力设置为气弹簧输出力最小值。在此条件下，气弹簧输出力最小值与设计目标的关系为：

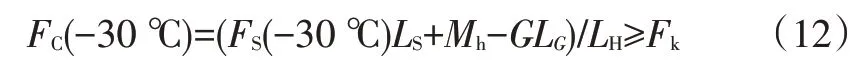
式中，FC(-30 ℃)为-30 ℃条件下气弹簧保证撑起发动机罩的最小压缩力；Fk为在-30 ℃条件下关闭发动机罩所需要预留的操作力安全余量，为设计目标值。

式（12）取等号时，FS(-30 ℃)=(FkLH-Mh+GLG)/LS，综合理想气体状态方程pV=nRT和压强公式F=pS，并根据气弹簧工作原理，推导可知：

式中，Tl为指定的开氏低温条件；Fl为Tl温度条件下的气弹簧力；Th为指定的开氏高温条件；Fh为Th温度条件下的气弹簧力。

根据式（13），由低温（-30 ℃）状态下的FS（-30 ℃)可以推导出常用的常温（20 ℃）、高温（80 ℃）状态下的气弹簧力。

3.5.2.2 气弹簧动态行程中输出力的计算

参考文献[7]，气弹簧在不同行程位置的反力分别为F2=KF1、F3=F1+2f、F4=F2+2f。其中，K为气弹簧刚度系数，f为气弹簧摩擦力。根据行程与力的比例关系，可以得到随气弹簧行程变化的输出力为：

式中，Lx为气弹簧的行程变量。

3.6 铰链阻力矩的计算

四连杆的铰链阻力矩Mh一般很小，且难以计算。一般可以根据类似铰链的阻力矩进行设定，也可以通过试验测定。

3.7 发动机罩开闭操作力计算

如图3所示，根据式（2）、式（4）转化，可以求得发动机罩开启操作力为：

发动机罩关闭操作力为：

4 基于Excel软件的编程与试验验证

4.1 基于Excel软件的编程

根据上述计算分析，应用Excel 软件编制了开启机构的计算程序，其输入界面如图8、图9所示。

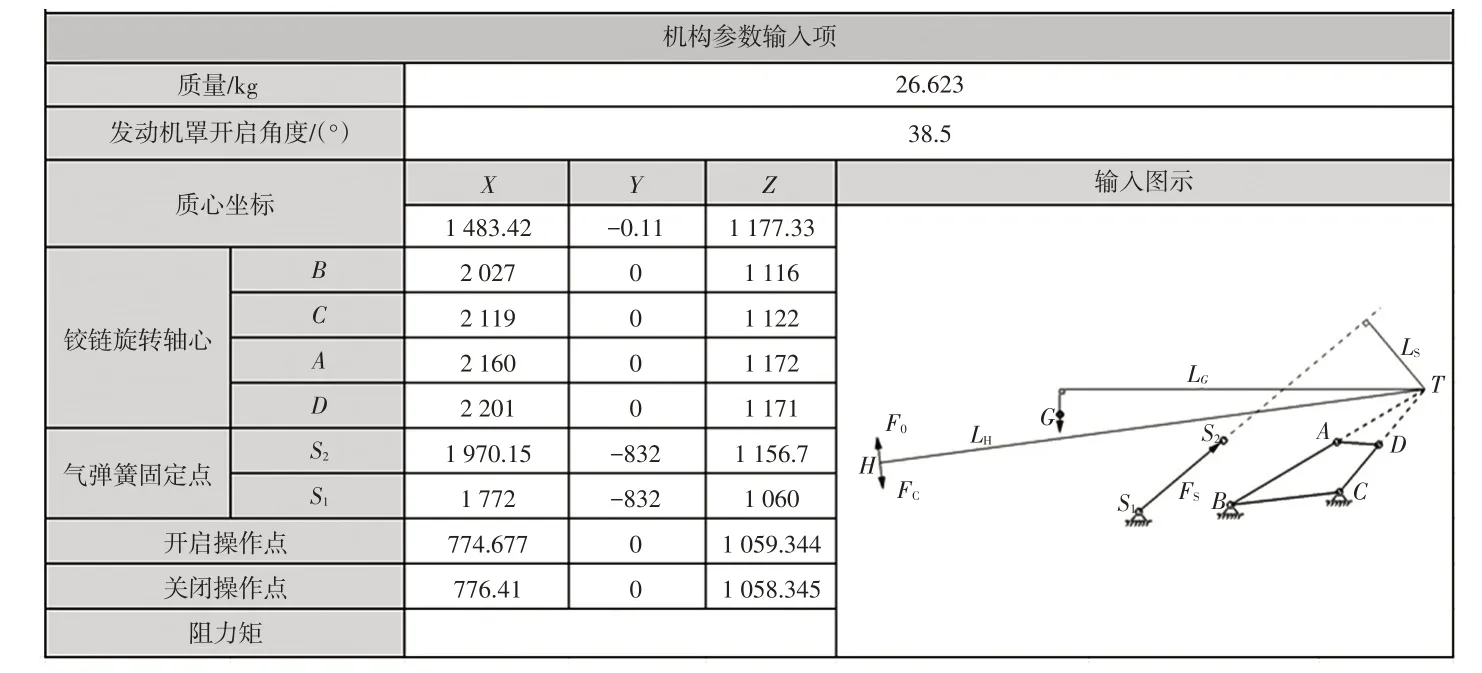
图8 机构参数输入界面

图9 气弹簧参数输入界面

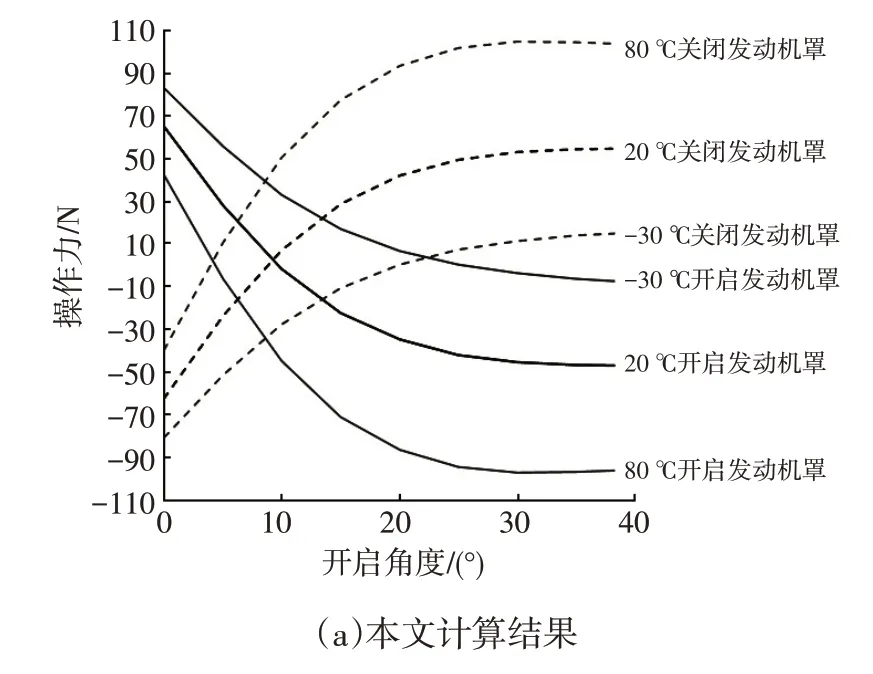
程序可以输出气弹簧特性力、行程、发动机罩开启和关闭的最大力、开闭操作力曲线图等。本文和国内某主流供应商针对某车型发动机罩开闭操作力的计算曲线输出结果如图10 所示，各温度下输出曲线符合度在95%以上。

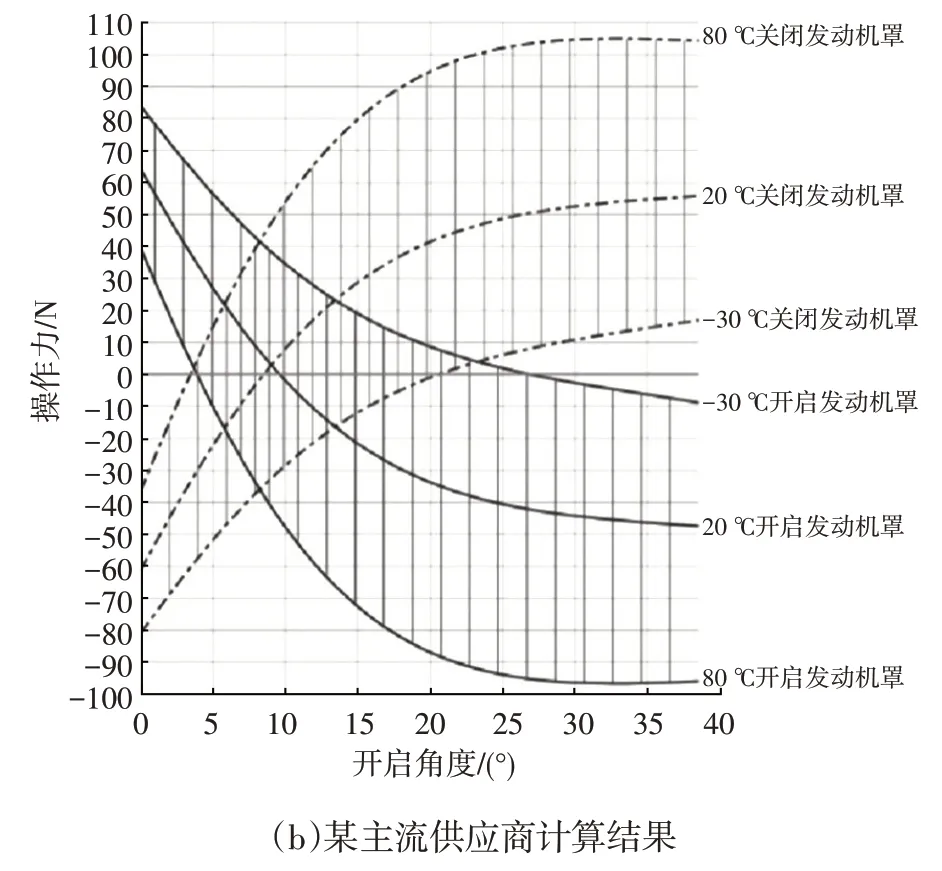
图10 某车型发动机罩开闭操作力曲线

4.2 试验验证

针对计算结果，选定某车型进行开闭操作力计算符合度的实车验证，试验环境温度为20 ℃，试验用气弹簧力为中值样件（力值偏差＜5 N），试验车发动机罩全开角度为38.5°，试验结果如表1所示。由于实车发动机罩开启时，锁体会将其弹起约0.8°，故实测数据从0.8°开始。

由表1 可知，在累积实车各项偏差后，计算的最大试验偏差在20%以内，可以为后续实车开发分析提供设计参考。

表1 发动机罩开闭操作力试验结果

5 计算结果的优化分析

发动机罩助力开启机构设计中重点关注开启和关闭操作力的大小、平衡角度的位置等影响用户体验的参数。初步计算输出的结果往往不能同时满足高温、常温、低温的开闭操作力工程目标要求，为了获取更优的结果，需要对计算参数进行优化。

5.1 发动机罩关闭操作力的优化分析

以常温下发动机罩的关闭操作力为例进行分析。

式（16）中，Mh很小，可以忽略，得到常温下操作力为：

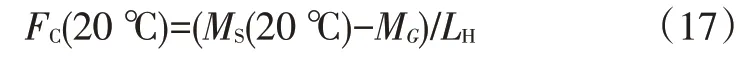
低温下，有MS(-30 ℃)=FkLH+MG，由式（13）变形可得：

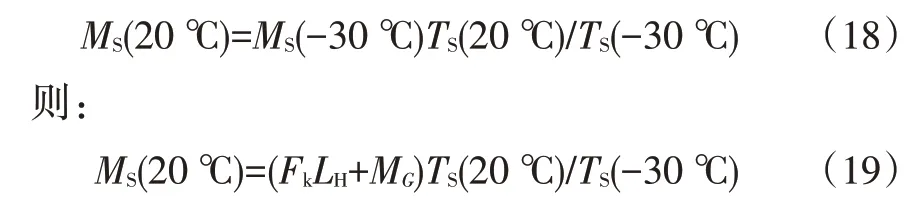
将式（19）代入式（17），整理可得：

根据式（20），可以得出以下结论：

a.发动机罩在常温下的关闭操作力，只与MG、LH、Fk有关，与LS无关，即通过调整气弹簧安装点的位置无法改变常温下关闭操作力的大小。

b.减小常温关闭操作力，可以通过减小Fk、MG或增大LH实现，但发动机罩结构一旦确定，MG和LH很难调整。所以实际应用中，调整关闭操作力的主要手段是牺牲部分Fk值。

5.2 发动机罩开启操作力的优化分析

由式（2）、式（19）可知，在MG和Fk不变的条件下，MS为定值，FS从发动机罩全开到全闭的变化率可以用Y表示，其值一般在1.1～1.4 范围内，读取Excel 程序中的气弹簧力臂LS的变化率Ys为2.4左右，即Ys≈2Y。这意味着在全开位置MS一定的条件下，LS所占的比值越高，MS到全闭位置的衰减越快，即需要更大的开启操作力才能打开发动机罩。全开与全闭位置的LS的变化方向一致，所以当关闭操作力一定时，可以通过增大LS来增大发动机罩开启操作力，减小LS来降低发动机罩开启操作力。这可以通过调整气弹簧的安装位置来实现。

5.3 发动机罩开启和关闭平衡角度的优化分析

由发动机罩开启操作力的分析过程和结果可得：当关闭操作力一定时，增大开启操作力，发动机罩开启的平衡角度增大，反之，发动机罩开启的平衡角度减小。根据上述结论可以调整优化发动机罩开启和关闭的平衡角度。

5.4 气弹簧刚度系数K的优化分析

K一般由供应商提供，当无法对MG、LH、固定点位置等参数进行优化时，可以考虑对K进行优化。根据K=F2/F1、理想气体状态方程和气弹簧工作原理，可以推得：

式中，V1为发动机罩全闭时气弹簧伸展状态下的气体工作体积；V2为发动机罩全开时气弹簧压缩状态下的气体工作体积。

由式（21）可知：如需减小K，可以同时增大V1和V2，即增加气弹簧缸筒的长度。由于受限于气弹簧布置和内部的结构实现条件，调整空间有限，调整的效果并不明显，所以建议在没有其他更好优化方式的情况下使用。通过Excel 程序测试，减小K可以使开闭操作力曲线更加平直，同时也可以增大开启操作力FO。

5.5 铰链轴心布置的优化分析

铰链各轴心的布置主要影响铰链的瞬心位置，进而影响各力臂及发动机罩的开闭操作力。本文对铰链瞬心位置的变化对发动机罩开闭操作力的影响进行分析。

5.5.1 关闭操作力

根据式（20）可知，当Fk为定值时，FC与LG/LH正相关，且有LG/LH＜1，当瞬心位置向车后方调整时，设调整量为Δx，可得：

随着瞬心位置向车后方调整，LG/LH有增大趋势，即FC会增大。但在实际调整中，Δx远小于LG和LH，其变化对关闭操作力的影响也很小，所以实际应用时，调整瞬心位置对关闭操作力的影响可忽略不计。

5.5.2 开启操作力

根据式（2）可知，FO=(GLG-FSLS)/LH（忽略铰链阻力矩）。调整铰链瞬心位置时，会导致多个变量变化，定量推导过于繁琐，通过Excel程序定性分析可知，随着瞬心的后移，FO逐渐下降。实际应用中可通过调整瞬心位置来优化FO。

6 结束语

本文针对目前气弹簧助力式四连杆铰链机构应用日益普遍的情况，提出了基于Excel 软件编程的操作力计算方法，同时针对计算结果从理论的角度给出了优化方向，包括开启操作力、关闭操作力、平衡角度、四连杆铰链轴心的优化。本文计算方法的理论结果与国内某主流供应商的计算结果符合度在95%以上；与实车试验值的最大偏差在20%以内；并首先从理论的角度给出操作力等的优化分析，其优化原理也适用于更简单的气弹簧助力式定轴铰链背门或发动机罩的操作力分析。未来将在现有成果的基础上，在参数自动优化驱动的气弹簧布置方向上开展更深入的研究。