基于滑模PI控制的卡尔曼滤波在空间转台的应用

叶 青 李 雪 冯 宇 李 宇 方智毅

上海宇航系统工程研究所，上海 201109

0 引言

永磁同步电机(permanent magnetic synchronous motor, 简称PMSM)因其功率密度高、体积小、功率因数高和优越的动态响应速度[1-2]，近年来被越来越广泛地应用于空间二维转台负载的驱动控制。由PMSM驱动的空间二维转台的超低速控制是一个新的研究领域。目前，空间二维转台负载对PMSM驱动系统最低转速要求可能达到0.05(°)/s左右，对控制精度的要求也相应地越来越高。超低速PMSM系统是强耦合、非线性的，如果将传统的PI控制+T法测速方法直接用于二维转台的超低速控制，则可能出现如下3个问题：1) T法测速的估计误差较大导致速度跟踪误差较大，达不到要求的精度；2) 超低速工况下的摩擦力矩呈非线性，电缆力矩与角度成正比，传统的PI控制难以消除这两个干扰力矩的影响；3) 负载和电机的物理系数(主要是力矩系数和转动惯量)的时变性导致：根据某一组系数确定的比例、积分系数不适用于所有的工况，传统的PI控制缺乏自适应性。

国内外学者在解决PMSM低速高精度控制问题上做了很多研究[3-5]，在观测器设计和滑模控制算法的应用方面有以下研究成果。文献[6]采用插值的方法增加观测器采样周期之间的采样点，提高了观测精度。文献[7]采用了卡尔曼滤波的方法获取更优的低速工况的转速。文献[8]采用了高频注入法，在低速控制时代替机械式位置传感器来获取速度角度信息。文献[9]设计模糊PI 滑模观测器提高系统的快速性和稳定性。文献[10]通过扩展卡尔曼滤波(简称EKF)实现磁链、转子位置和速度的精确估计，提高了直接转矩控制的性能。文献[11]设计的EKF观测器，把光电码盘信号的量化误差考虑为测量噪声，提升了转子位置、速度的观测精度。文献[12]利用EKF对电机的电阻、电感参数进行识别，有效地改善了PMSM控制性能。文献[13]设计分数阶滑模变结构控制器，来提升系统的动态、稳态性能和鲁棒性。文献[14]采用模糊PID技术与滑模观测器的新型混合估计策略，进一步提高了系统转子位置和电机转速的观测精度。文献[15]在直接转矩控制中运用变指数趋近律滑模变结构控制策略，有效地抑制了滑模变结构的抖振，并且改善了转矩和磁链的脉动过大的问题。文献[16]设计了一种积分型滑模变结构控制器，通过观测负载转矩并反馈到滑模控制器中，使系统具有响应快速、无超调等优点，且对负载的力矩扰动具有较强的鲁棒性。文献[17]提出了一种上下界滑模变结构速度控制器，将速度误差与系统状态量的变化相关联，通过预设负载转矩的上下界值，实时改进滑模控制律，有效地提高系统的静态、动态特性与鲁棒性。

由于卡尔曼滤波算法和滑模控制算法在工程上都有较强的实用性，因此可以考虑将二者结合起来，应用于空间二维转台的超低速控制。本文主要针对空间二维转台PMSM的速度环设计展开研究。针对二维转台超低速控制的应用场景，提出了一种基于滑模PI控制的卡尔曼滤波算法来改进传统的PI控制+T法测速方法。这一算法的优势体现在如下3个方面：1) 卡尔曼滤波算法将滑模PI控制的抖振看作是白噪声，再根据测量噪声的随机分布特性，提取出更准确的转速信息，提高控制精度；2) 将摩擦力矩和电缆力矩看作是低频干扰，消耗一定的控制力矩来消除低频干扰对转速控制性能的影响；3) 考虑了实际应用中力矩系数和转动惯量的时变性，用Lyapunov方法确定滑模PI控制律中的控制参数，使得闭环系统必然稳定。为验证基于滑模PI控制的卡尔曼滤波算法的可行性，本文设计了仿真试验，将该算法与传统的PI控制+T法测速方法进行了对比。

1 滑模PI控制算法理论分析

本节假定系统状态可以准确测量，只讨论滑模PI控制律的设计方法，状态估计方法的讨论在下一节中展开。本文中，电流环采用SVPWM算法[18]。在本节假定q轴电流[18]实际值与指令值总是相等的。

考虑某型二维空间转台PMSM速度环的被控系统模型

(1)

其中，t表示时间，J表示转动惯量，ω表示机械角速度，b表示力矩系数，iq表示q轴电流，df表示摩擦力矩的大小，dθ>0表示电缆力矩系数，θ表示机械角。假设时变参数满足：Jmin≤J(t)≤Jmax，bmin≤b(t)≤bmax，0≤df(t)≤dfmax。Jmax,bmin,dfmax,dθ>0已知，Jmin,bmax>0未知，这种参数给定在型号研制中常见。

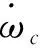
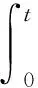
根据式(1)，关于z1,z2的系统模型方程可写成

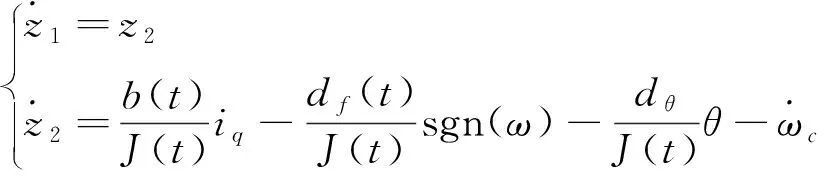
(2)

设控制律

iq=u0+v

其中PI控制律u0为

u0=-Kiz1-Kpz2

其中，Ki>0为积分系数，Kp>0为比例系数，现需要确定滑模控制律v。

设

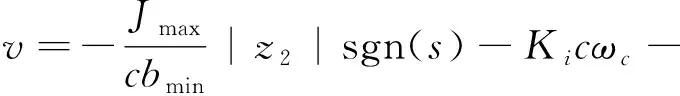
(3)

其中滑模变量

s:=z1+cz2+cωc,c=Kp/Ki

开关变量

σ1=1,当sω<0时,σ1=0,其他

σ2=1,当sθ<0时,σ2=0,其他

常增益ks>0为任意小的正常数。下面给出定理1。

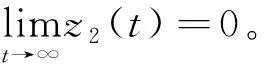
证明：设第一个Lyapunov函数为

则对V1求导，再代入控制律(3)，得到

所以当s≠0时，s在有限时间内收敛为0。当s=0时，再设第2个Lyapunov函数

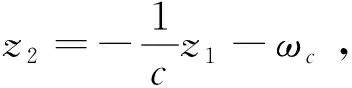
所以如果在时刻t0时s(t0)=0，则在任意时刻t>t0，当t→∞时，

s(t)≡0⟹V2(t)→0⟹z1(t)→-cωc⟹z2(t)→0

所以闭环系统渐近稳定，证毕。

从式(3)中可见，滑模PI控制律需要已知的变量包括：θ,ω,Jmax,bmin,dfmax,dθ,dmax。其中：θ,ω需要用卡尔曼滤波算法进行估计；Jmax,bmin,dfmax,dθ是负载的固有物理量，可以经过事先实验测得；dmax取决于位置环的控制律，是已知的。

可以看出滑模PI算法有以下3个优点：1) 需要在线估计的物理量较少，有可操作性；2) 只需已知转动惯量上界和力矩系数下界，所以这一算法是通过施加强控制力来使系统稳定：只要增加控制力，就能提高鲁棒性；3) 传统PI控制律需要同时控制2个变量：跟踪误差和其积分，而滑模PI控制律只需控制一个变量s，这对于超低速工况是实用的。

2 卡尔曼滤波算法

本文提出的卡尔曼滤波算法参考了文献[19]的设计，但是在处理干扰力矩方面有所不同。

伺服系统的匀速运动离散化方程为

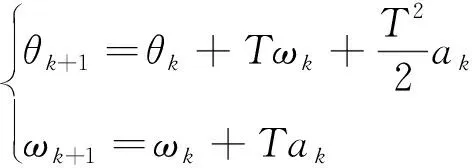
(4)

式中，下标k表示该变量为第k个采样周期的变量。基于(4)的卡尔曼滤波的过程及测量方程如下：

其中，X=[θ,ω]T为状态变量，a表示角加速度，z为角度测量值，w,v分别为过程噪声和测量噪声，A,B,C定义为：

卡尔曼滤波算法如下：

(5)

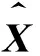
在算法(5)的实施中需要已知角加速度ak，电机匀速转动时ak约等于0，但是在仿真试验中可以发现如果令ak恒等于0，则滤波性能较差。根据式(1)可知，ak的准确值应为

其中，iqk为第k个周期的q轴电流值，可以在线测量，但是在实际工程中b(t),J(t),df(t)未必已知，且θk和ωk尚需要进行估计。因此本文中提出ak的估计方法为

这一估计方法与文献[19]不同，优点是：避免了控制与状态观测的耦合，信号的因果关系明确，易于工程实现。

3 基于滑模PI控制的卡尔曼滤波算法在空间转台超低速控制中的应用

在空间轨道运行的某型号高精度转台上的负载由PMSM拖动。PMSM的控制通常由外到内分为三环：位置环、速度环和电流环。一个典型的三环控制框图如图1所示。

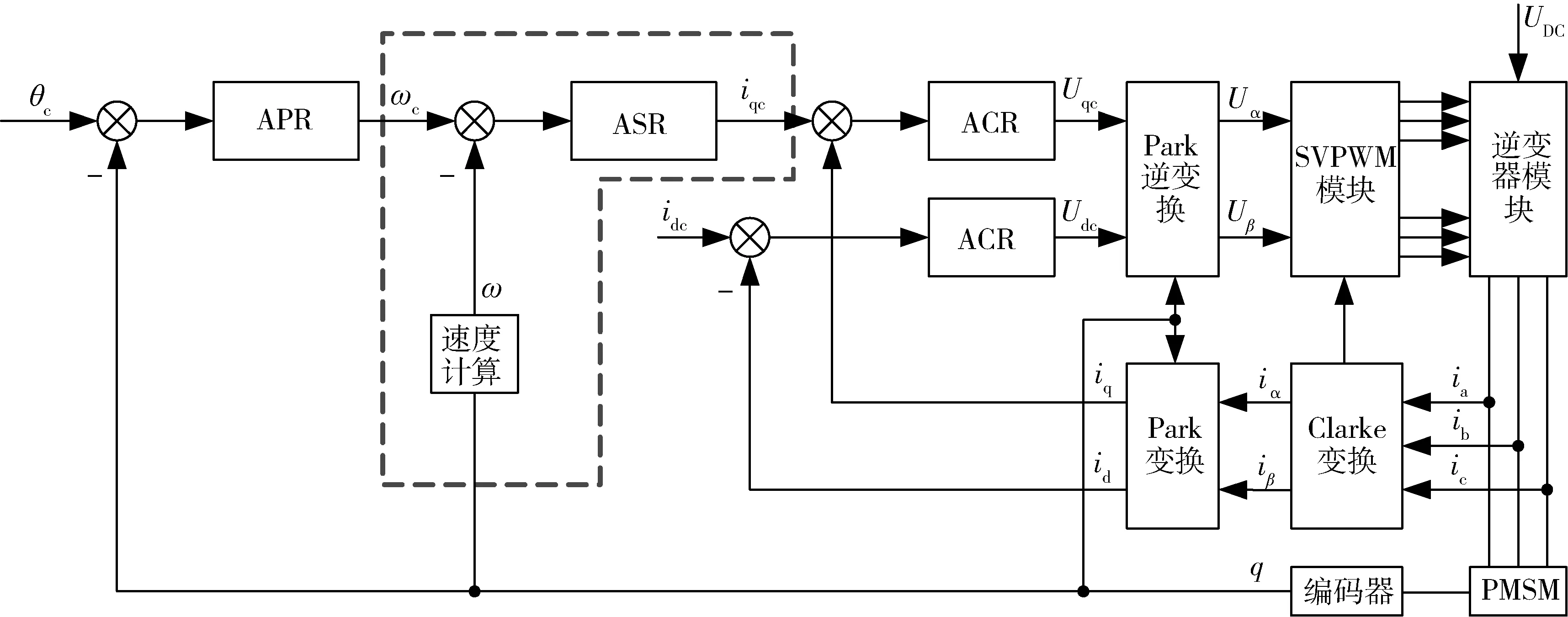
图1 PMSM的三环控制结构

图1中APR，ASR和ACR分别表示位置环、速度环和电流环控制律，本文提出的算法可以被用来改进绿色虚线框中的环节。在空间高精度二维转台的一些应用场景中，要求负载绕方位轴和俯仰轴缓慢地匀速转动，对一定范围的空间区域进行扫描。这一具体要求体现在PMSM系统中，可以抽象为：位置环输出恒定非零的速度环指令，要求PMSM转速以足够高的精度稳态精度可能要求达到0.01(°)/s跟踪恒定的速度环指令。当速度环指令很小(可能达到0.05(°)/s)时，会带来难以解决的控制问题，主要体现在如下3个方面：

1)电机转速过低时，无法用传感器直接测量速度，需要从角度信息中提取出速度信息；

2)摩擦力矩和电缆力矩在系统模型中呈现非线性，低速运行时，静摩擦力的影响不可忽视；

3)由于二维转台两轴间的耦合性，绕方位轴的转动惯量会有很大幅度的变化，可能影响控制性能。

本文提出了基于滑模PI控制的卡尔曼滤波算法来解决这3个问题。综合考虑第1节和第2节的算法，进行控制和状态估计一体化设计：在每时每刻利用前一采样时刻的估计值，用第2节的卡尔曼滤波算法求出当前时刻的估计值，然后将这一估计值代入到第1节的滑模PI控制律中求解电流环指令。这样得到的基于滑模PI控制的卡尔曼滤波算法如下：

2)根据算法(5)计算出Xk,Pk，令θk=Xk(1),ωk=Xk(2)；

3)计算z2:=ωk-ωc，z1:=z1+Tz2；

4)计算PI控制输入和滑模控制输入：

u0k=-Kiz1-Kpz2

(6)

其中

σ1k=1,当sωk<0时，σ1k=0,其他

σ2k=1,当sθk<0时，σ2k=0,其他

5)输出电流环指令iqck=u0k+vk。

由于这一算法常用于转台的恒定转速控制，因此可以取定dmax=0。

基于滑模PI控制的卡尔曼滤波算法的控制框图如图2所示。

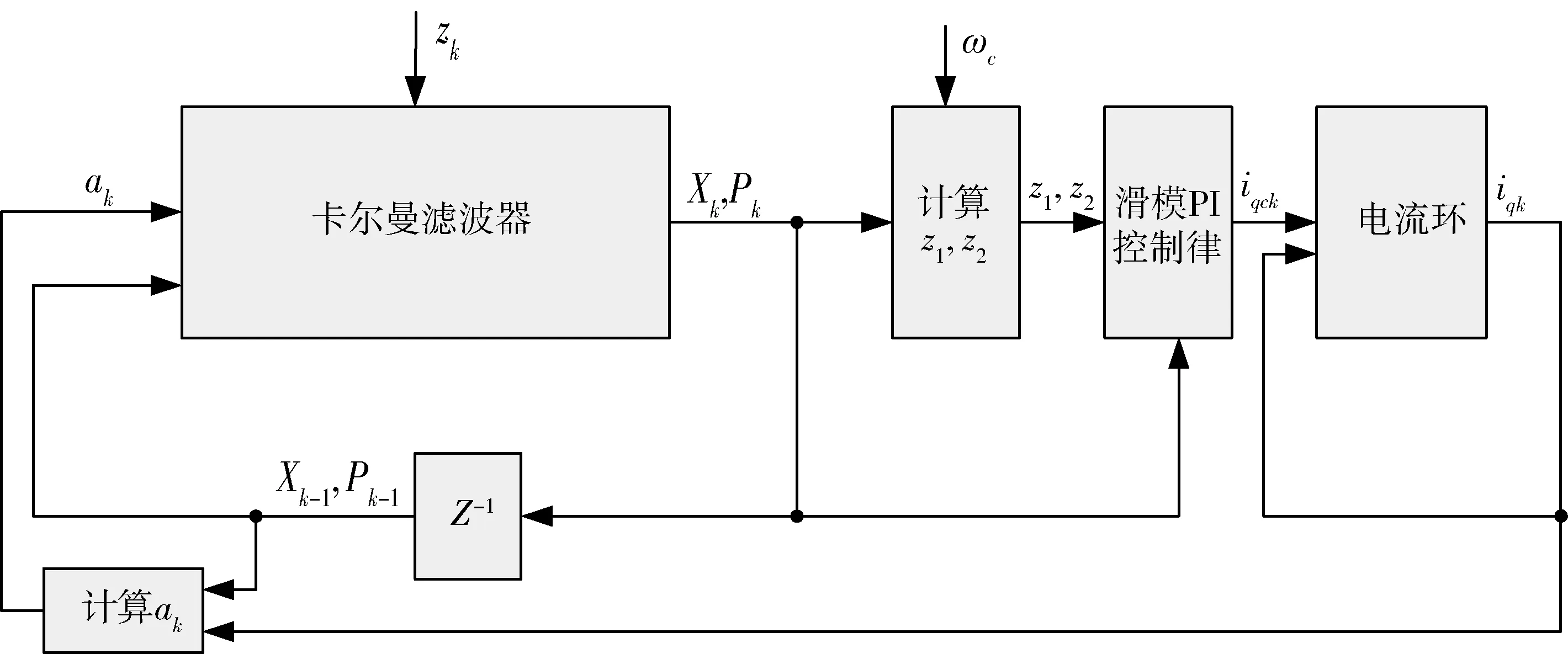
图2 控制框图

针对二维转台超低速控制面临的3个控制问题，基于滑模PI控制的卡尔曼滤波算法在以下3个方面予以解决：

1)卡尔曼滤波器的设计考虑了滑模控制固有的抖振现象，可以根据电流环输出和位置环输出估计出较为准确的角速度，根据文献[20]的定理2.10可知，卡尔曼滤波器能够实现无偏估计。

2)由定理1的证明可知，滑模控制算法以尽可能大的控制力使滑模变量收敛为0，使得摩擦力矩和电缆力矩对滑模变量的收敛速度没有影响，进而对速度跟踪误差的收敛性没有影响。

3)由式(3)可见，滑模PI控制律不需要已知当前的转动惯量大小，只需已知转动惯量的最大值，再由定理1的证明可知转动惯量的变化对系统稳定性没有影响，对滑模变量的收敛速度也没有影响。

4 仿真校验

根据某型二维转台负载和电机型号确定模型参数，其中J≤12kg·m2，b≥7N·m/A，转动惯量时变，按照图1搭建Simulink仿真模型，用基于滑模PI控制的卡尔曼滤波算法改进速度环。现给定角度测量干扰的标准差为0.001°，要求速度跟踪的稳态跟踪误差在0.01(°)/s以下。

首先给出超低速工况(速度跟踪指令为0.05(°)/s)下的仿真结果，与传统的PI控制+T法测速方法进行了对比，如图3所示。

图3 超低速工况下的仿真曲线

由图3可见，卡尔曼滤波算法保证在超低速工况下速度估计误差始终在0.006(°)/s以下，如图3(c)所示。同时从图3(c)中可见T法测速的估计误差远远大于卡尔曼滤波的估计误差，这会引起控制性能的下降。滑模PI控制算法保证了速度跟踪性能良好，如图3(a)所示。由图3(d)可见q轴电流始终在0.2A内变化。由图3(b)可见，基于滑模PI控制的卡尔曼滤波算法保证速度跟踪的稳态误差在0.005(°)/s以下，满足控制精度要求，而传统方法不能满足设计要求。

由图3(b)可见本文提出的算法并不能保证跟踪误差在0(°)/s左右变动，这是因为卡尔曼滤波器对速度估计始终有一个正的偏差，如图3(c)所示。这可能是卡尔曼滤波算法中对干扰的估计不精确引起的。更多的仿真试验结果表明，随着速度指令的提高，速度估计的偏差逐渐减小，直到不明显。而速度跟踪精度与速度指令基本无关，始终能够保持跟踪精度小于0.01(°)/s。在不同速度指令下，本文提出的算法与PI控制+T法测速方法的控制精度对比如图4所示。

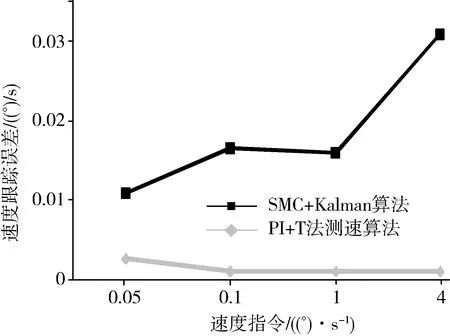
图4 不同速度指令下跟踪精度对比

从图4可见，本文提出的算法在速度指令提高时精度更高，而传统方法正好相反。这是因为T法测速在速度指令提高时，差分运算时会引入更大的噪声。

下面给出速度指令阶跃变化工况下的速度响应，速度指令为0.05(°)/s→0.25(°)/s→0.15(°)/s。仿真结果如图5所示。

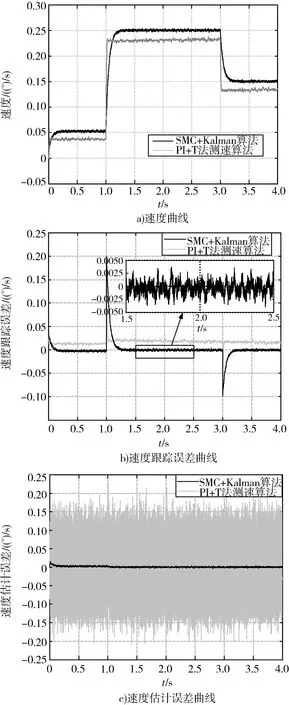
图5 阶梯速度指令下的仿真曲线

仿真结果表明卡尔曼滤波的速度估计误差始终在0.004(°)/s以下，如图5(c)所示。同时滑模控制算法保证了速度跟踪性能良好，速度动态接近一阶惯性环节，如图5(a)所示。由图5(b)可见，速度跟踪的稳态误差在0.004(°)/s以下，满足控制精度要求。

5 结论

提出了一种基于滑模PI控制的卡尔曼滤波算法，用于空间高精度二维转台上PMSM的低速控制。这种算法改进了传统的PI控制+T法测速方法，有以下3个优点：1)卡尔曼滤波算法能够更准确地估计较低的转速，提高控制精度；2) 能够克服非线性干扰力矩引起的低频干扰；3) 对模型不确定性具有足够强的鲁棒性。仿真试验结果表明，当PMSM运行于低速区域时，本文提出的算法对环境噪声有足够强的鲁棒性，能够保证闭环系统的速度跟踪性能良好；在超低速工况下，本文算法保证速度跟踪精度较PI控制+T法测速更优，且速度估计误差远低于PI控制+T法测速。