生产管柱泄漏气井油套环空起压模式对比

陆努 ，张波 ，胥志雄 ，娄尔标 ，罗方伟 ，谢俊峰 ，刘洪涛 ，赵效锋

（1.中国石油勘探开发研究院，北京 100083；2.中国石油安全环保技术研究院，北京 102206；3.中国石油塔里木油田分公司，新疆 库尔勒 841000；4.中国石油塔里木油田分公司油气工程研究院，新疆 库尔勒 841000；5.中国石化中原油田分公司石油工程技术研究院，河南 濮阳 457001）

0 引言

四川盆地、塔里木盆地和南海等区域的气田气井均存在不同程度的环空带压现象，严重影响气井的长期安全稳产［1-3］。受井下高温高压、复杂载荷和腐蚀流体的影响［4-5］，生产管柱泄漏成为环空起压的主要原因之一。如BP公司阿拉斯加州某油田区块［6］，生产管柱接箍和管体的微小泄漏占泄漏点总数的50%以上；中东［7］、墨西哥湾［8］和国内区块［9］的现场数据也证实了这一观点。生产管柱泄漏引起的环空起压，呈现压力高、压力上升速度快且周期性恢复的特点［10］。气井环空起压对气井井口、封隔器、水泥环的完整性和日常管理的危害很大。

为此，国内外学者开展了各类背景下的生产管柱泄漏和环空起压方面的研究。1999年，Adam等［11］指出了众多与环空压力相关的恶性事故都是由于生产管柱泄漏造成的；2012年，朱红钧等［12］认为生产管柱泄漏是CO2注入井环空带压的主要原因，并分析了CO2由注入管柱进入环空的过程及分布形态；2016年，朱达江等［13］提出了一种利用压力恢复测试资料计算生产管柱泄漏速率的方法；2018年，武胜男等［14］提出了基于U型管原理定位生产管柱泄漏点的算法；2019年，罗伟等［15］研究了高含硫气井生产管柱泄漏导致的环空异常起压问题，并根据现场经验定性分析了环空起压模式。以上研究极大地促进了油气井生产管柱泄漏的防控与管理，但未能对气井环空起压模式进行定量对比，不利于快速判断生产管柱的失效程度，以及评价环空带压风险。本文以生产管柱泄漏气井为研究对象，基于气体的PVT性质和液体温压效应，构建了环空压力计算模型。以小孔模型和划分时间段的方法来计算气体泄漏量，考虑气体上升过程中与地层之间的热交换和环空气液分布动态变化，解析了泄漏点处的温压分布。利用所建立的模型，对比了4种典型环空起压模式下的压力上升周期、泄漏速率、液面高度和气体聚积体积等参数，评价了不同环空起压模式的风险，提出了快速判断管柱泄漏程度的方法及相应的控制建议。

1 环空压力计算模型

气体泄漏后聚集在气井环空上部形成气柱，在温压效应影响下，环空内液柱体积也发生了变化。当环空保护液未发生泄漏时，气柱体积与液柱体积之和始终等于环空体积，这符合体积相容性原则［16-17］。气、液柱体积大小均与环空压力、井筒温度分布情况相关，可通过建立气、液柱体积关系式来求解环空压力：

式中：Vag为环空气柱体积，m3；Val为环空初始液柱体积，m3；ΔVal为环空液柱体积变化量，m3；Van为环空体积，m3；ΔVan为环空体积变化量，m3；Vagc为环空气柱初始体积，m3。

1.1 环空气柱体积

环空气柱体积大小与泄漏量、井筒温压分布有关。生产管柱泄漏点一般在接箍丝扣或较小的腐蚀孔处，因而可视为具有节流效应的孔洞，其标况泄漏速率为

式中：QLg为泄漏点标况泄漏速率，m3/s；Co为流量系数；Al为泄漏点当量面积，m2；ρgs为气体标况密度，kg/m3；R为气体常数，取值 8.341 4 J/（mol·k)；Tfl为泄漏点温度，K；CRE 为临界压力比；pal，pfl分别为泄漏点外压、内压，Pa；kg为气体绝热指数；Mg为气体摩尔质量，kg/mol；Zgl为泄漏点气体压缩因子（可由 Ehsan公式［17］获得）。

由于压力处于动态变化中，将时间划分成步长为Δt的分段。当步长足够短时，认为单个时间段内的温压稳定，则进入环空中的气体标况总体积Vg为

式中：Vgs为环空初始气体标况体积，m3；sj为时间分段数量；j为时间分段编号；Qlg，j为第j时间段生产管柱泄漏点的标况泄漏速率，m3/s。

根据气体的PVT性质，考虑环空温度分布和压力变化，Vag计算公式为

式中：Tagc为环空气柱温度，K；Ts为标况温度，K；ps为标况压力，Pa；pac为环空气柱初始压力，Pa；Δpa为环空压力变化量，Pa；Zga为环空气体压缩因子；Zgs为标况下环空气体压缩因子。

1.2 环空液柱体积及环空体积变化量

Δpa与环空液体温度变化量ΔTa、环空液柱体积变化量ΔVal、进出环空的液体质量变化量Δm呈全增量微分关系［18］，即：

式中：Ta为环空液体温度，K；pa为环空压力，Pa；m 为进出环空的液体质量，kg。

当环空液体未发生泄漏时，式（6）中的Δm=0。结合等温压缩系数和等压膨胀系数的定义，式（6）可转化得到 ΔVal，即：

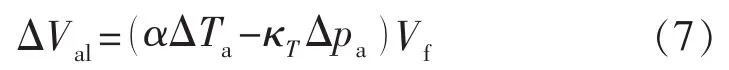
式中：α为环空液体等压膨胀系数，K-1；κT为液体等温压缩系数，MPa-1。

环空体积变化是由油套管径向位移引起的，考虑到温度沿井筒纵向的非线性分布特征，将井筒划分为等长度段，ΔVan为各分段体积变化量的累加，即：

式中：M为环空起始深度所对应的井筒分段编号；i为井筒分段编号；hw为井深，m；ΔVan，i为第 i段井筒环空体积变化量，m3；Δz为井筒分段长度，m。

根据热弹性平面应变问题和弹性力学轴对称问题的求解［19］，可得到环空内外半径变化量，则 ΔVan，i为

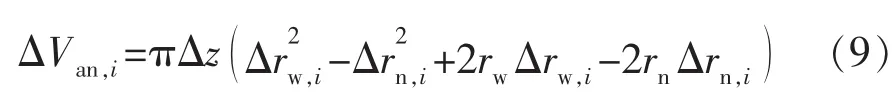
式中：rw为环空外半径（即环空外侧套管内半径），m；rn为环空内半径（即环空内油管外半径），m；Δrw，i为第 i段井筒环空外半径变化量，m；Δrn，i为第i段井筒环空内半径变化量，m。

2 气井温压及流体分布计算

2.1 生产管柱内

泄漏点内部温压取决于生产管柱温压分布。在油管柱内取长度为dz的微元体，微元体内符合动量守恒和能量守恒定律，即：

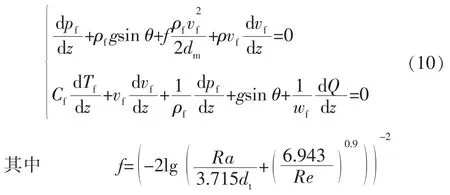
式中：pf为生产管柱内的压力，Pa；ρf为生产管柱内的气体密度，kg/m3；θ为井斜角，（°）；f为摩擦系数；vf为气体流速，m/s；Cf为气体比热容，J/（kg·K）；Tf为气体温度，K；wf为气体质量流量，kg/s；Q 为井筒径向热流量，J/s；g 为重力加速度，m/s2；Ra 为油管柱粗糙度，m；dt为油管柱内径，m；Re为雷诺数。

井筒内外和地层之间的传热过程符合井筒径向热传导理论，因此井筒外边缘温度Th和径向热流量分别为

式中：Rto为井筒内径向传热热阻，m·K/W；λe为地层导热系数，W/（m·K）；Te为地层温度，K；TD为无因次地层温度（根据文献［20］计算得到）；下标D表示无因次。

联立式（10）、（12），则生产管柱内的气体密度、速度、黏度与温压的耦合关系可分别用气体PVT、质量守恒和萨特兰公式来表征；然后，以井筒分段差分的方式获取第i+1段井筒中生产管柱内的温度Tf，i+1（t）和压力 pf，i+1（t）：

式中：pf，i为第i段井筒中生产管柱内的压力，Pa；Tes，i+1为第i+1段井筒内的生产管柱所对应地层温度，K；fi+1为第i+1段井筒内的生产管柱摩擦系数；为为 第第ii++11段段井筒中生产管柱内的气体流速，m/s；Δvf，i+1为第 i+1 段井筒中生产管柱内的气体流速变化量，m/s；ρf，i+1为第 i+1段井筒中生产管柱内的气体密度，kg/m3；下标i+1为第i+1段井筒。

2.2 环空内

环空温压分布决定了泄漏点外压和环空流体状态。根据井筒径向热传导理论，取环空中间位置温度作为环空流体温度，则第i段环空流体温度Ta，i为

式中：Rzro，i为第i段井筒内环空的中间位置至油管柱中心的热阻，m·K/W；Rto，i为第 i段井筒内径向传热热阻，m·K/W；Tf，i为第 i段井筒内气体温度，K；Th，i为第 i段井筒外边缘温度，K；Te，i为第i段井筒相对应的地层温度，K。

同时认为，环空流体在气井投产前与地层进行了充分的热交换，其初始温度与地层温度相等，则环空液体温度变化量ΔTa为

式中：N为油套环空液面对应的井筒分段编号；L为环空液体起始深度对应的井筒分段编号。

pal与环空压力、环空流体压力相关，计算公式为

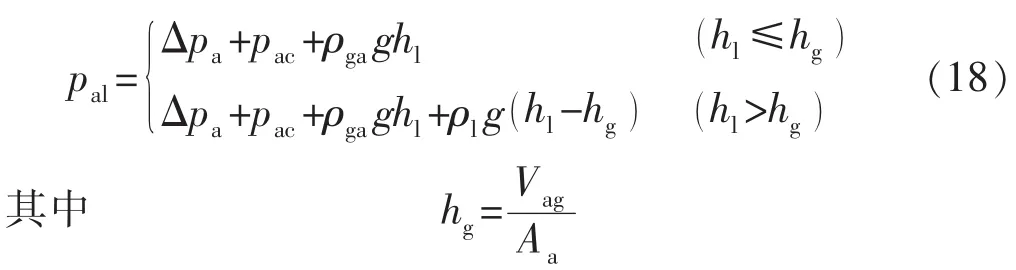
式中：ρga为环空内气体密度，kg/m3；ρl为环空液体密度，kg/m3；hl为泄漏点所在深度，m；hg为环空液面深度，m；Aa为环空横截面积，m2。

3 典型环空起压模式特征

以某深层高压气井为例，该井人工井底深度650 m，射孔段介于6 730～6 810 m，封隔器深度6 680 m，初始油套环空液柱长度6 431.5 m，产层温度173.07℃，产层压力119 MPa，地温梯度2.51℃/100 m，产气量60×104m3/d。

根据现场经验，环空起压模式可设定为4种类型：1）大孔浅层，孔径 2.5 mm，深度 1 000 m；2）大孔深层，孔径2.5 mm，深度5 000 m；3）小孔浅层，孔径0.5 mm，深度 1 000 m；4）小孔深层，孔径 0.5 mm，深度 5 000 m。假设在该井投产300 d后发生泄漏，井筒分段长度为1 m，时间步长为 20 s，流量系数为 0.8（见表 1）；再利用本文模型，对环空起压模式特征进行分析。

表1 计算参数

3.1 环空起压过程

总体上，环空压力随着时间的延长而上升，且上升速度逐渐变缓，最终趋于稳定。气体泄漏速率先稳定不变，然后随时间延长而下降，并最终趋于0（见图1）。

图1 环空压力及泄漏速率随时间的变化规律

对比图1中4种环空起压模式可知：泄漏点孔径对环空压力上升周期影响极大，泄漏点孔径越大，泄漏速率越大，环空压力上升周期越短，但对环空压力最大值无影响，泄漏点深度决定了环空压力最大值，泄漏点深度的增加将缩短环空压力上升周期；在叠加作用下，大孔深层与小孔浅层的环空压力上升周期出现了数量级差距，分别为83.33，3 996.66 min。虽然深层泄漏的前期环空压力上升速度快，但在同一环空压力上升周期内，浅层泄漏的总体起压速度明显高于深层泄漏。

3.2 环空流体分布

由图2可以看出：气体泄漏导致环空内气体体积的增加及液面深度的降低，但变化趋势均放缓，并最终趋于平稳。需要注意的是，这里的气体体积是在标准状况下的气体体积，而不是气柱体积。

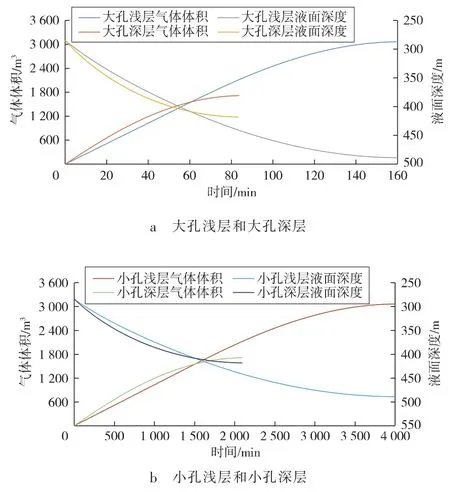
图2 环空气体体积及液面高度随时间的变化规律

对比图2中环空起压模式可知：环空气体体积的最大值、液面深度都与泄漏点深度相关，泄漏点孔径大小只影响其变化周期；虽然液体压缩性较小，但由于环空压力大及环空液柱长，在压缩效应作用下，环空液面明显降低，从而为不断增加的气体提供空间。深层和浅层泄漏点的气体体积分别为1 714.29，3 065.21 m3。

4 环空起压模式对比

4.1 泄漏风险

综上所述，浅层泄漏点引起的环空压力具有压力上升周期长、压力高的特征。较大孔径情况下的环空起压速度快，压力上升周期短，其泄漏速率初始数值大。因此，4种典型环空起压模式在环空压力及压力上升周期、泄漏速率、环空内聚积气体体积等参数上具有差异性。环空压力越大，井筒屏障的安全可靠性所受影响也越大。因而环空压力上升速度快、上升周期短对环空压力风险的预警和控制不利，环空内聚积气体体积越大，则放喷难度越大。本文对4种典型环空起压模式的风险进行了定性评价（见表2）。由表可知：大孔浅层泄漏具有环空压力高、速度快、聚积气体体积大的特征，风险最高；相反，小孔深层泄漏风险最低。

表2 典型环空起压模式的特征与风险评价

4.2 泄漏程度

对比同一深度（5 000 m）、不同孔径泄漏点的环空压力上升周期可以看出，其值与泄漏点孔径的关系密切（见图 3）。

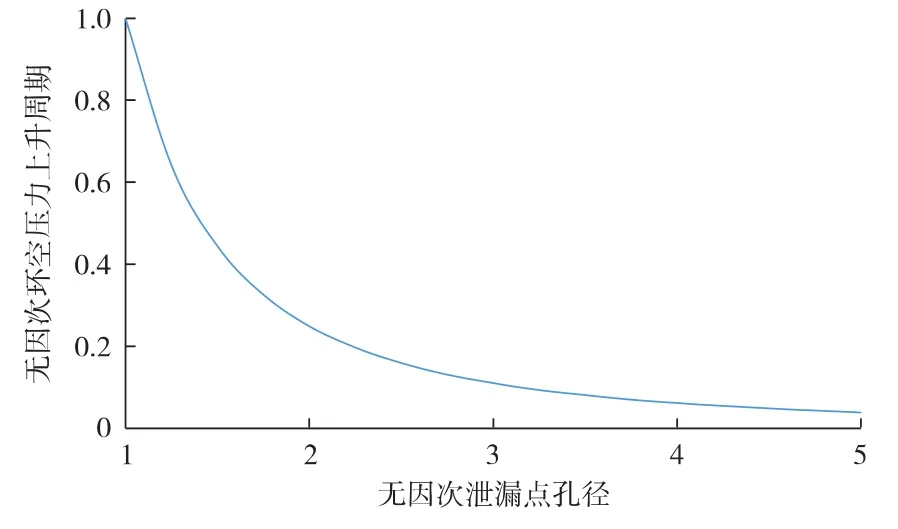
图3 无因次环空压力上升周期与无因次泄漏点孔径的关系

式中：tz为环空压力上升周期，min；t1为泄漏点孔径1 mm时的环空压力上升周期，min。

在泄漏点深度确定的前提下，利用环空压力上升周期与泄漏点孔径的关系，可迅速获取泄漏点孔径，来判断生产管柱泄漏程度。以A井为例，该井泄漏点孔径为0.500 0 mm，深度为5 000 m，该处环空压力上升周期为2 093 min，利用式（19）计算得到的泄漏点孔径为0.503 6 mm，与实测值比较，误差仅为0.72%。

4.3 压力值控制

泄漏点深度决定了环空压力最大值。通常情况下，当环空压力低于最大允许环空压力时，风险可控，且能监控生产。从计算模型可知，环空压力最大值等于泄漏点外部液柱压力与泄漏点所在深度的油管内部压力之差。考虑到关井状况生产管柱内压力升高，可以根据生产管柱内部压力分布来确定泄漏深度阈值hdl，当泄漏点深度大于hdl时，环空压力最大值始终小于最大允许压力，即：

式中：pmax为最大允许环空压力，Pa；ptc为环空流体产生的压力，Pa；h为井深，m；pfs为关井状态下生产管柱内压力，Pa。

因此，可以有针对性地加强该深度上部管柱的完整性设计，避免丝扣密封失效和腐蚀穿孔等，确保气井安全生产。当A井泄漏点深度大于3 462 m时，环空压力最大值小于最大允许环空压力（64.5 MPa）。

5 结论

1）不同环空起压模式的环空压力值、压力上升速度、压力上升周期和环空内聚积的气体体积等参数具有差异性，浅层的泄漏点引起的持续环空压力具有压力上升速度快、上升周期长和压力高的特征；泄漏点孔径的增大虽然不会改变压力数值，但会导致泄漏速率和环空压力上升速度的大幅上升，其中，大孔浅层泄漏风险最高，小孔深层泄漏风险最低。

2）泄漏点孔径对环空压力上升周期影响大。同一深度下，无因次环空压力上升周期与无因次泄漏点孔径为幂函数关系，可用于快速判断生产管柱泄漏程度。环空压力最大值取决于泄漏点深度，根据关井状态下的生产管柱内压力分布、最大允许环空压力和环空内流体产生的压力，可确定泄漏深度阈值，以加强该深度以上的管柱完整性设计，避免发生大孔浅层泄漏现象。