关于丢番图方程x2+144=my11(m=1,2,3,4,6)的整数解

陈一维， 白建慧

(华北水利水电大学 数学与统计学院，河南 郑州 450046)

0 引言

丢番图方程是数论中最古老的一个分支，也是一个重要的分支，它有着悠久的历史与丰富的内容,与数学学科的其他分支也有着密切的联系。高次的多元不定方程还有广阔的未知领域，吸引着众多学者。所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程或方程组，其未知数的个数通常多于方程的个数。其最早可追溯到3世纪初，当时古希腊数学家丢番图研究过许多这样的方程，因此不定方程又称为丢番图方程。

设A,B∈N，A无平方因子，关于不定方程

Ax2+B=myn(x,y,n∈N,n≥2)

(1)

解的问题是数论中的一个重要问题，用初等方法解决此类问题比较复杂和困难，近些年许多研究者用代数数论的方法研究这类不定方程，取得了很好的成果。

2009年，文献[1]证明了当A=1,B=16,m=1,n=13时，(1)式无整数解；2011年，文献[2]证明了当A=1,B=144,m=3,n=19时，(1)式无整数解；2018年，文献[3]证明了当A=1,B=1 024,m=4,n=9时，(1)式仅有整数解(x,y)=(±32，2)；2018年，文献[4]证明了当A=1,B=1 024,m=1,n=11时，(1)式仅有整数解(x,y)=(±32，2)；2019年，文献[5]证明了当A=1,B=36,m=1,n=17时，(1) 式无整数解;2019年，文献[6]证明了当A=1,B=4 096,m=4,n=11时，(1)式仅有整数解(x,y)=(±64，2)。

本文主要讨论当A=1,B=144,m=1,2,3,4,6,n=11时，(1)式的整数解问题。

1 定理及其证明

引理1[1]设M是唯一分解整环，正整数k≥2,α,β∈Z,(α,β)=1,若αβ=τk,τ∈M，则有α=ε1μk,β=ε2νk,μ,ν∈M, 其中ε1,ε2是M中的单位元素，并且ε1ε2=εk,ε为单位元素。

定理1不定方程

x2+144=my11(y=1,2,3,4,6),x,y∈Z

(2)

无整数解。

证明分x≡1(mod 2)和x≡0(mod 2)两种情况进行讨论。

情况1x≡1(mod 2)。

当x≡1(mod 2)时，在Z[i]中，式(2)可以写为(x+12i)(x-12i)=my11,x,y∈Z。设(x+12i,x-12i)=η,则有η|(2x,24i),得η只能取1,1+i,2,因为x≡1(mod 2)，因此x+12i≡1(mod 2)，则η≠2；假设η=1+i，则N(1+i)|N(x+12i),即2|x2+144。这就与x≡1(mod 2)产生矛盾，所以η=1。由此和引理1得，x+12i=m(a+bi)11,x,a,b∈Z，则有

x=a11-55a9b2+330a7b4-462a5b6+165a3b8-11ab10,

(3)

12=mb(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10),

(4)

所以方程有如下取值

1)当m=1时；(4)式变为

12=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)。

(5)

a)当b=1时，由(5)式得

12=11a10-165a8+462a6-330a4+55a2-1,

(6)

13=a2(11a8-165a6+462a4-330a2+55),

(7)

由(7)式得，a2=1 ，但当a2=1时，11-165+462-330+55=33≠13所以b=1不成立。

b)当b=-1时，由(5)式得

-12=11a10-165a8+462a6-330a4+55a2-1，

(8)

-11=a2(11a8-165a6+462a4-330a2+55),

(9)

由(9)式得，a2=1，当a2=1时，11-165+462-330+55=33≠-11，所以b=-1不成立。

c)当b=2 时，由(5)式得，

6=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(10)

1 030=103×5×2=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(11)

由(11)式得，a2=1，当a2=1时，11-660+7 392-21 120+14 080=-297≠1 030，故b=2不成立。

d)当b=-2时，由(5)式得

-6=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(12)

1 018=2×509=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(13)

由(13)式得，a2=1，当a2=1时，11-660+7 392-21 120+14 080=-297≠1 030，故b=-2不成立。

e)当b=3时，由(5)式得

4=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(14)

59 053=1×59 053=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(15)

由(15)式得，a2=1，但当a2=1时，11-1 485+37 422-240 570+360 855=156 233≠59 053，故b=3不成立。

f)当b=-3时，由(5)式得

-4=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(16)

59 045=5×49×241=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(17)

由(17)式得，a2=1或49，但当a2=1时，

11-1 485+37 422-240 570+360 855=156 233≠59 045,

但当a2=49时

49×(11×494-165×9×493+462×92×492-330×93×49+55×94)≠59 045,

故b=-3不成立。

g)当b=4时，由(5)式得

3=11a10-165×16a8+462×162a6-330×163a4+55×164a2-165,

(18)

1 048 579=7×149 797=a2(11a8-165×16a6+462×162a4-330×163a2+55×164),

(19)

由(19)式得，a2=1，但当a2=1时

11-2 640+118 272-1 351 680+3 604 480=2 368 443≠1 048 579，

故b=4不成立。

h)当b=-4时，由(5)式得

-3=11a10-165×16a8+462×162a6-330×163a4+55×164a2-165,

(20)

1 048 573=1×1 048 573=a2(11a8-165×16a6+462×162a4-330×163a2+55×164),

(21)

由(21)式得，a2=1，但当a2=1时

11-2 640+118 272-1 351 680+3 604 480=2 368 443≠1 048 573，

故b=-4不成立。

i)当b=6时，由(5)式得

2=11a10-165×36a8+462×362a6-330×363a4+55×364a2-365,

(22)

60 466 178=2×17×1 778 417=a2(11a8-165×36a6+462×362a4-330×363a2+55×364),

(23)

由(23)式得，a2=1，但当a2=1时

11-5 904+598 752-15 396 480+92 378 880=77 575 223≠60 466 178，

故b=6不成立。

j)当b=-6时，由(5)式得

-2=11a10-165×36a8+462×362a6-330×363a4+55×364a2-365,

(24)

60 466 174=2×30 233 087=a2(11a8-165×36a6+462×362a4-330×363a2+55×364),

(25)

由(25)式得，a2=1，但当a2=1时

11-5 904+598 752-15 396 480+92 378 880=77 575 223≠60 466 174，

故b=-6不成立。

k)当b=12时，由(5)式得

1=11a10-165×144a8+462×1442a6-330×1443a4+55×1444a2-1445,

(26)

61 917 364 225=25×29×85 403 261=
a2(11a8-165×144a6+462×1442a4-330×1443a2+55×1444),

(27)

由(27)式得，a2=1或25，但当a2=1时

11-23 760+9 580 032-985 374 720+23 648 993 280=22 673 174 843≠61 917 364 225，

且当a2=25时

故b=12不成立。

l)当b=-12时，由(5)式得

-1=11a10-165×144a8+462×1442a6-330×1443a4+55×1444a2-1445,

(28)

61 917 364 223=11×13×432 988 561=
a2(11a8-165×144a6+462×1442a4-330×1443a2+55×1444),

(29)

由(29)式得a2=1，但当a2=1时

11-23 760+9 580 032-985 374 720+23 648 993 280=22 673 174 843≠61 917 364 223，

故b=-12不成立。

2)当m=2时，

12=2×b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10),

即

6=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)。

(30)

a)当b=1时，由(30)式得

6=11a10-165a8+462a6-330a4+55a2-1,

(31)

7=a2(11a8-165a6+462a4-330a2+55),

(32)

由(32)式得a2=1，但当a2=1时11-165+462-330+55=33≠7，故b=1不成立。

b)当b=-1时，由(30)式得

-6=11a10-165a8+462a6-330a4+55a2-1,

(33)

-5=a2(11a8-165a6+462a4-330a2+55),

(34)

由(34)式得a2=1，但当a2=1时11-165+462-330+55=33≠-5，故b=-1不成立。

c)当b=2时，由(30)式得

3=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(35)

1 027=13×79=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(36)

由(36)式得a2=1，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 027，故b=2不成立。

d)当b=-2时，由(30)式得

-3=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(37)

1 021=1×1 021=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(38)

由(38)式得a2=1，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 021，故b=-2不成立。

e)当b=3时，由(30)式得

2=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(39)

59 051=1×59 051=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(40)

由(40)式得a2=1，但当a2=1时

11-1 485+37 422-240 570+360 855=156 233≠59 051，

故b=3不成立

f)当b=-3时，由(30)式得

-2=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(41)

59 047=137×431=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(42)

由(42)式得a2=1，但当a2=1时

11-1 485+37 422-240 570+360 855=156 233≠59 047，

故b=-3不成立。

g)当b=6时，由(30)式得

1=11a10-165×36a8+462×362a6-330×363a4+55×364a2-365,

(43)

60 466 177=37×1 634 221=a2(11a8-165×36a6+462×362a4-330×363a2+55×364),

(44)

由(44)式得a2=1，但当a2=1时

11-5 904+598 752-15 396 480+92 378 880=77 575 223≠60 466 177，

故b=6不成立。

h)当b=-6时，由(30)式得

-1=11a10-165×36a8+462×362a6-330×363a4+55×364a2-365,

(45)

60 466 175=7×11×25×101×311=a2(11a8-165×36a6+462×362a4-330×363a2+55×364),

(46)

由(46)式得a2=1或25，但当a2=1时

11-5 904+598 752-15 396 480+92 378 880=77 575 223≠60 466 175，

且当a2=25时

故b=-6不成立。

3)当m=3时

12=3×b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)，

即

4=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)。

(47)

a)当b=1时，由(47)式得

4=11a10-165a8+462a6-330a4+55a2-1,

(48)

5=a2(11a8-165a6+462a4-330a2+55),

(49)

由(49)式得a2=1，但当a2=1时11-165+462-330+55=33≠5，故b=1不成立。

b)当b=-1时，由(47)式得

-4=11a10-165a8+462a6-330a4+55a2-1,

(50)

-3=a2(11a8-165a6+462a4-330a2+55),

(51)

由(51)式得a2=1，但当a2=1时11-165+462-330+55=33≠-3，故b=-1不成立。

c)当b=2时，由(47)式得

2=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(52)

1 026=2×3×9×19=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(53)

由(53)式得a2=1或9，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 026，且当a2=9时9×(11×94-165×4×93+462×42×92-330×43×9+55×44)=124 047≠1 026,故b=2不成立。

d)当b=-2时，由(47)式得

-2=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(54)

1 022=2×7×73=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(55)

由(55)式得a2=1，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 022，故b=-2不成立。

e)当b=4时，由(47)式得

1=11a10-165×16a8+462×162a6-330×163a4+55×164a2-165,

(56)

1 048 577=17×61 681=a2(11a8-165×16a6+462×162a4-330×163a2+55×164),

(57)

由(57)式得a2=1，但当a2=1时11-2 640+118 272-1 351 680+3 604 480=2 368 443≠1 048 577，故b=4不成立。

f)当b=-4时，由(47)式得

-1=11a10-165×16a8+462×162a6-330×163a4+55×164a2-165,

(58)

1 048 575=3×11×25×31×41=a2(11a8-165×16a6+462×162a4-330×163a2+55×164),

(59)

由(59)式得a2=1或25，但当a2=1时11-2 640+118 272-1 351 680+3 604 480=2 368 443≠1 048 575，且当a2=25时

25×(11×254-165×16×253+462×162×252-330×163×25+55×164)=169 483 875≠1 048 575,

故b=-4不成立。

4)当m=4时

12=4×b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10),

即

3=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10),

(60)

a)当b=1时，由(60)得

3=11a10-165a8+462a6-330a4+55a2-1,

(61)

4=a2(11a8-165a6+462a4-330a2+55),

(62)

由(62)式得a2=1或4，但当a2=1时11-165+462-330+55=33≠4，且当a2=4时4×(11×44-165×43+462×42-330×4+55)=-6 468≠4，故b=1不成立。

b)当b=-1时由(60)式得

-3=11a10-165a8+462a6-330a4+55a2-1,

(63)

-2=a2(11a8-165a6+462a4-330a2+55),

(64)

由(64)式得a2=1，但当a2=1时11-165+462-330+55=33≠-2，故b=-1不成立。

c)当b=3时，由(60)式得

1=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(65)

59 050=2×25×1 181=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(66)

由(66)式得a2=1或25，但当a2=1时 11-1 485+37 422-240 570+360 855=156 233≠59 050，且当a2=25时

25×(11×254-165×9×253+462×92×252-330×93×25+55×94)=-29 272 375≠59 050,

故b=3不成立。

d)当b=-3时，由(60)式得

-1=11a10-165×9a8+462×92a6-330×93a4+55×94a2-95,

(67)

59 048=2×4×121×61=a2(11a8-165×9a6+462×92a4-330×93a2+55×94),

(68)

由(68)式得a2=1或4或121或484，但当a2=1时11-1 485+37 422-240 570+360 855=156 233≠59 048，且当a2=4时 4×(11×44-165×9×43+462×92×42-330×93×4+55×94)=-379 588≠59 048，且当a2=121时

121×(11×1214-165×9×1213+462×92×1212-330×93×121+55×94)=29 805 566 153≠59 048,

且当a2=484时

484×(11×4844-165×9×4843+462×92×4842-330×93×484+55×94)=

214 855 200 960 092≠59 048,

故b=-3不成立。

5)当m=6时

12=6×b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10),

(69)

即

2=b(11a10-165a8b2+462a6b4-330a4b6+55a2b8-b10)。

(70)

a)当b=1时，由(70)式得

2=11a10-165a8+462a6-330a4+55a2-1,

(71)

3=a2(11a8-165a6+462a4-330a2+55),

(72)

由(72)式得a2=1，但当a2=1时11-165+462-330+55=33≠3，故b=1不成立。

b)当b=-1时，由(70)式得

-2=11a10-165a8+462a6-330a4+55a2-1,

(73)

-1=a2(11a8-165a6+462a4-330a2+55),

(74)

由(74)式得a2=1，但当a2=1时11-165+462-330+55=33≠-1，故b=-1不成立。

c)当b=2时，由(70)式得

1=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(75)

1 025=25×41=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(76)

由(76)式得a2=1或25，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 025，且当a2=25时

25×(11×254-165×4×253+462×42×252-330×43×25+55×44)=-47 738 625≠1 025，

故b=2不成立。

d)当b=-2时，由(70)式得

-1=11a10-165×4a8+462×42a6-330×43a4+55×44a2-45,

(77)

1 023=3×11×31=a2(11a8-165×4a6+462×42a4-330×43a2+55×44),

(78)

由(78)式得a2=1，但当a2=1时11-660+7 392-21 120+14 080=-297≠1 023，故b=-2不成立。

所以当x≡1(mod 2)时，不定方程x2+144=my11(m=1,2,3,4,6)无整数解。

情况2x≡0(mod 2) 。

1)m=1,3。

已知x≡0(mod 2)，x是偶数，则y也是偶数，令x=2x1,y=2y1,x1,y1∈Z。则(2)式等价为

(2x1)2+144=m(2y1)11,

即

(79)

(80)

(81)

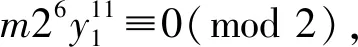
2)m=2，则原方程变为

x2+144=2y11。

(82)

(83)

(84)

(85)

3)m=4，则原方程变为

x2+144=4y11。

(86)

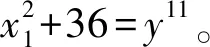
4)m=6，则原方程变为

x2+144=6y11。

(87)

所以当x≡0(mod 2) 时，不定方程x2+144=my11(m=1,2,3,4,6)无整数解。

综上所述，不定方程x2+144=my11(m=1,2,3,4,6)无整数解。

2 结语

不定方程的整数解问题是一个悠久的研究课题，许多数学家都有所研究，推进了不定方程整数解问题的发展。本文主要讨论了当A=1,B=144，m=1,2,3,4,6,n=11的整数解问题，得出了不定方程x2+144=my11(m=1,2,3,4,6)无整数解的结论和证明。接下来希望可以进一步研究不定方程x2+144=my11(m∈N)的整数解问题。