一种基于区间数的投资组合选择模型

范国兵， 赵宗智， 严建明

(湖南财政经济学院 数学与统计学院，湖南 长沙 410205)

0 引言

1952年，诺贝尔经济学奖获得者MARKOWITZ H发表了著名的论文《Portfolio selection》[1]，最先提出了均值—方差投资组合选择模型，创造性地运用数理分析方法研究金融资产的收益—风险关系。此后，证券投资组合问题研究吸引了国内外众多学者，成为一个研究热点。GIOVE S等[2]研究了把资产的价格看成区间数，基于后悔函数的极小极大后悔值法的证券投资组合模型；WANG HAIYANG[3]提出了不完全市场中具有不连续价格和随机水平的均值—方差投资组合选择模型；薛巧玲等[4]利用极大熵原理提出了一种基于区间极大熵的多目标规划模型；李荣钧[5]提出了基于模糊数的多目标线性规划模型。

投资选择的基本目标是追求收益最大化和风险最小化，实践中流动性也是证券市场的重要属性。由于证券市场的各种不确定性，投资者对于风险、收益、流动性等很难给出确定值，因而带有模糊数的投资组合选择模型的研究更有意义。本文在现有文献的基础上，建立模糊环境下以证券组合投资的期望收益率为目标函数，以组合投资的风险、流动性为约束条件，兼顾收益、风险、流动性的区间规划证券投资组合模型，给出了模型求解的方法，并通过实例分析，验证模型的有效性。

1 问题描述

1.1 有关区间数的符号和定义[6]

1.2 模型建立

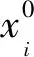
假定投资组合调整的过程中没有注入新的资金，采用Ⅴ型交易数函数，则投资组合x=(x1,x2,…,xn,xn+1)的总交易费用为

故扣除交易费后，投资组合的净收益为

现考虑对投资收益的满意程度，建立s型的隶属函数

从而投资组合的风险与换手率分别表示为

从而可以建立模糊环境下以证券组合投资的模糊期望收益率为目标函数，以组合投资的风险、流动性为约束条件的区间规划投资模型

(1)

1.3 模型求解

设投资风险和换手率满足定义2中的悲观满意指数λ，则模型(1)可转化为

(2)

根据引理1，模型(2)等价于

(3)

对于模型(3)，可利用Lingo软件包求解[7]。

2 应用实例

以文献[8]中的相关数据为例，5只股票的相关数据如表1。

表1 5只股票相关数据Tab.1 Relevant data of 5 stocks

假设投资者将资产分配到5种风险资产(5只股票)和1种无风险资产投资(用银行1年定期储蓄代替)上，预先给定的风险承受区间β值的区间为[0.6,3.0]，流动性(换手率)接受区间为[0.10，0.60]，风险资产的交易费用为0.000 5，无风险资产的交易费为0。适当取定模型(11)中的参数，利用Lingo求解得到优化方案如表2。

表2 投资组合优化方案表Tab.2 Scheme of Portfolio optimization

相对而言，方案1是结合投资者比较保守的心态得到的最优投资组合；而方案2是结合投资者比较积极的心态得到的最优投资组合。

3 结论

投资组合选择是投资者在不确定环境下的投资决策问题，证券市场中，投资收益、风险和流动性都是不确定的，利用模糊数描述组合投资的收益率，利用区间数描述风险损失率和流动性的不确定性，建立了一种基于区间数的证券投资组合模糊规划模型，该模型将区间数理论和模糊决策理论结合，用隶属函数刻画投资者对收益的满意度，用PSD(pessimism satisfaction data)刻画对投资组合的风险和换手率的满意程度。投资者可根据自己的偏好，选定模型中的满意度参数，得到相应的投资决策优化方案，在实际应用中具有较大的灵活性。