两步Shepard插值组合模型在构建局部似大地水准面中的应用

王俊杰 滕 雷 佴 晋 王隆安

(山东科技大学 测绘科学与工程学院, 山东 青岛 266590)

0 引言

利用全球定位系统(Global Positioning System，GPS)技术和重力场模型构建局部似大地水准面的关键在于高程异常的获取,通常采用“移去—恢复法”与拟合模型相结合的方法[1-6]。郑荃心将Shepard拟合与二次曲面拟合相结合,得出该方法拟合效果较好[7];方懿基于某测区数据,结合Matlab软件,得出二次多项式曲面拟合与BP神经网络相结合的组合方法拟合精度较高[8];杨丹等对多面函数拟合法中核函数的选取进行分析[9]。现有文献中Shepard插值在构建局部似大地水准面方面应用较少,少有的应用也仅涉及一类模型,未能形成系统性的应用成果。本文拟通过多项式曲面、多面函数和神经网络等3种方法下属的12类模型与Shepard插值分两步相结合进行精度分析,探讨组合模型的优越性。

1 Shepard插值

Shepard插值为统计模型内插算法,实质是反距离加权的最小二乘法,适用于大规模散乱数据拟合问题。其权函数表达式如式(1)所示[10]:

(1)

式中，d为样本点间的距离;R为影响半径,取d的平均值。待求点的属性值见式(2):

(2)

式中，ξj为待求点属性值;ξi为已知点属性值;n为待求点个数。

2 组合模型

2.1 基础模型

常用于高程拟合的数学模型有多项式曲面、多面函数、神经网络等。

2.1.1多项式曲面

多项式曲面是在高程异常和地面之间建立一定的函数映射关系,进行局部高程拟合。

多项式曲面模型如式(3)所示[11]:

ξ=f(X,Y)=a0+a1X+a2Y+a3X2+

a4Y2+a5XY+…

(3)

式中，ξ为高程异常;ai为待拟合参数;X与Y为地面点的大地纬度和经度。根据参数的个数又可分为一次多项式、相关曲面、二次多项式和三次多项式等。

2.1.2多面函数

多面函数拟合是利用一系列有规则的数学曲面逼近局部似大地水准面[12]。其表达式为式(4):

(4)

式中，ξ为高程异常;ki为待定系数;Q(x,y,xi,yi)为核函数。核函数多选择对称的简单函数,通过对几种常用核函数的对比分析,提出一种简单核函数的通用公式,见式(5):

Q(x,y,xi,yi)=C+[(x-xi)2+(y-yi)2+σ]γ

(5)

式中，γ分别取-0.5、0.5和1.5;σ为平滑因子。根据是否添加常数项或平滑因子可分为正双曲面、倒双曲面、锥面、三次曲面等。

2.1.3神经网络

这里使用两种神经网络模型:①BP神经网络是最传统的神经网络模型,在处理非线性映射问题上具有很强的自组织能力；②径向基(RBF)神经网络是一种新颖的前馈式三层神经网络,可以加快学习速度并避免局部极小问题,本次基函数选择二次多项式[13]。

2.2 两步Shepard组合模型的建立

基础数学模型求得的高程异常ξ,残差曲线难免会出现波动和残差值过大的奇异点,基于Shepard插值思想的组合模型可以提高拟合精度。组合模型的步骤为:

(1)根据已知点数据,用基础模型求出已知点和未知点的高程异常拟合值ξ0和ξ1,获得已知点高程异常残差Ø1;

(2)第一步Shepard插值,按式(1)进行定权,以已知点高程异常为属性值,通过式(2)求出未知点高程异常拟合值ξ2;

(3)第二步Shepard插值,定权方式同上,以Ø1为属性值,通过式(2)求出残差改正值σ1;

(4)ξ2与σ1相减,即可求出未知点的高程异常拟合值。

虽然Shepard插值单独使用光滑性和光顺性较差,但数学拟合模型的使用弥补了这一点,数学模型拟合整体变化趋势,Shepard插值调整局部奇异点,结合两种模型优点的组合模型,整体和局部相结合,提高拟合精度。

2.3 精度评定

采用内符合精度、外符合精度、极差和效率公式对拟合结果进行精度评定。内、外符合精度公式如式(6)所示[14]:

(6)

式中，n1、n2分别为拟合点和检核点的数量,V为残差值。极差为残差中最大值与最小值的差值,公式为式(7):

∂=δmax-δmin

(7)

式中，∂为极差,δmax和δmin为残差中最大值与最小值。

效率公式为式(8):

(8)

式中，T为效率,t1为基础模型功效,t2为组合模型功效。

3 算例分析

算例为香港部分地区公开的控制点数据、高精度水准测量数据及GPS高程数据,该地区面积约为400 km2,地表起伏变化较为缓和。大地坐标参考框架为ITRF96,高程基准为香港高程基准面(Hong Kong Principal Datum，HKPD),点位高程数据通过精密水准测量测得,点数42个,位置如图1所示。分别选择21个已知点和检核点,通过不同的基础模型和对应的组合模型进行精度对比分析。

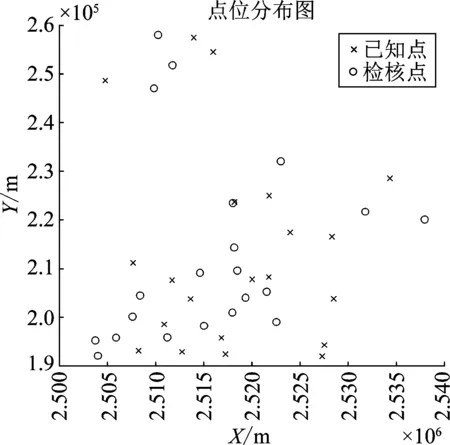
图1 点位分布图

3.1 基于多项式曲面的组合模型

四种多项式及其对应的组合模型残差曲线如图2所示。

图2 四种多项式及组合模型残差

从图2可以看出,多项式曲面模型中段波动较为平缓,前、后半段波动较为剧烈且有残差过大的奇异点出现;随着参数增加,残差曲线整体平稳度提升,但后半段奇异点的影响变大,最大为13.28 cm,奇异点出现的原因包括测量误差、选取的GPS水准点分布不合理等。组合模型中,基于一次曲面的组合模型残差曲线整体变化不大;其他三种组合模型残差曲线前半段拟合效果较好,残差曲线接近0值,后半段效果较差,出现个别残差改正过大情况,具体精度对比如表1所示。

由表1可知,基于四种多项式曲面的组合模型,外符合精度较原来有所提高,最大为三次多项式,提高了14%,最小为一、二次多项式,提高了3%,平均提高8%;极差均有降低,最大的为相关曲面,降低了29%,最小的为三次多项式,降低了11%,平均降低21%。

表1 四种多项式组合模型精度对比

3.2 基于多面函数的组合模型

选择核心点个数为11个,且在区域内均匀选取,设置相同的平滑因子, 六种多面函数及其对应的组合模型残差曲线如图3所示[15]。

在图3中,六种多面函数拟合模型整体趋势平缓,除核函数为加常数正双曲面的多面函数模型外,其余5种15、16号残差值较大,最大达到17.16 cm。奇异点出现的原因包括测量误差、核心点位置不合理、平滑因子不合理等。基于多面函数的组合模型对15、16号点位残差较大情况具有较好的平滑效果,但在18、19号点位出现轻微的改正过大现象,最大为6.14 cm。总体来说残差曲线波动变小,拟合效果较好,具体精度对比如表2所示。

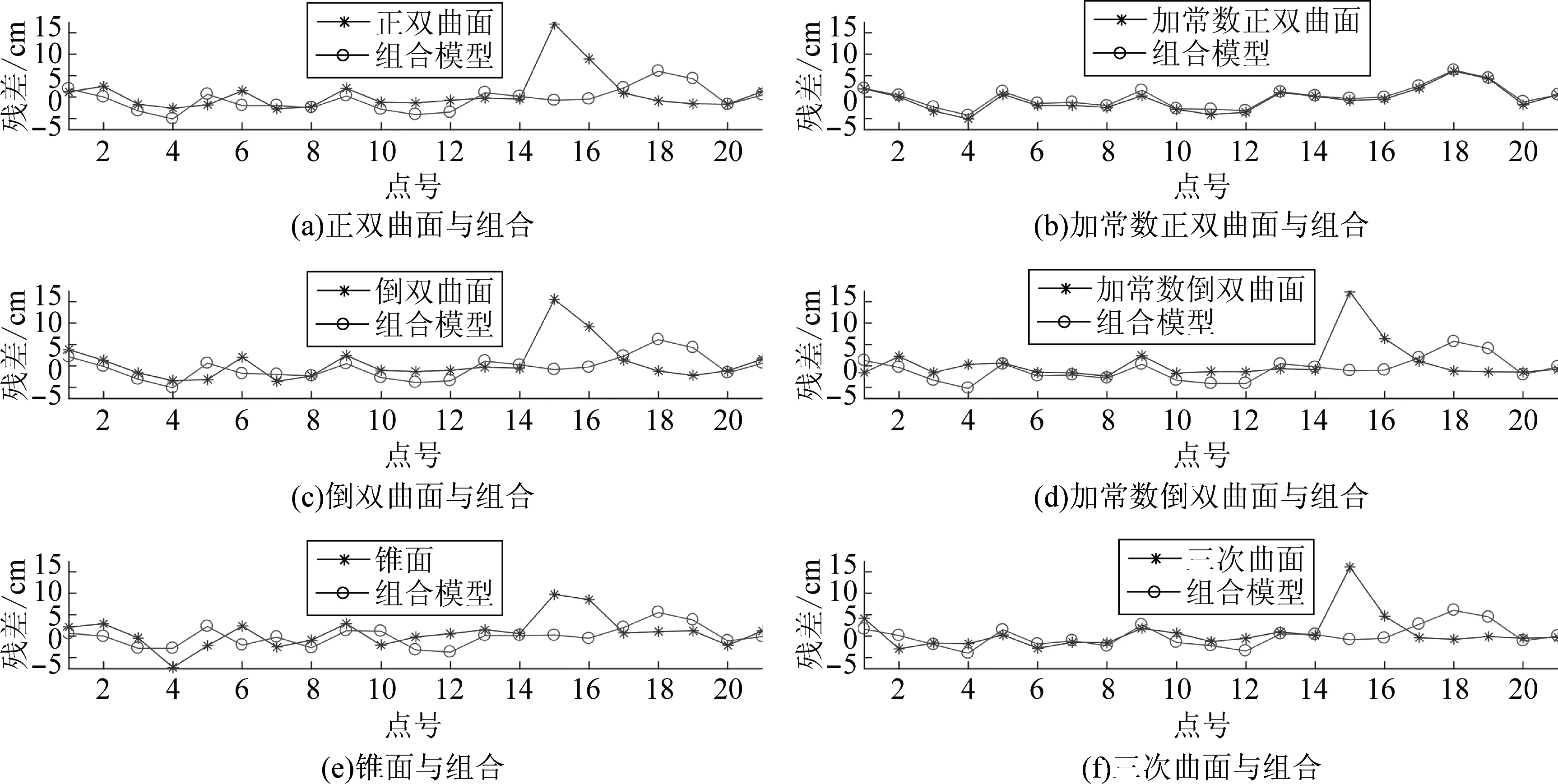
图3 六种多面函数及组合模型残差

从表2可以看出,基于多面函数的组合模型,外符合精度均有提高,最大为加常数正双曲面,提高了40%,最小为加常数倒双曲面,提升了35%,平均提升38%;极差均有降低,其中三次曲面较其他方法降低最多,为47%,最小的为加常数正双曲面,降低了5%,平均降低38%。

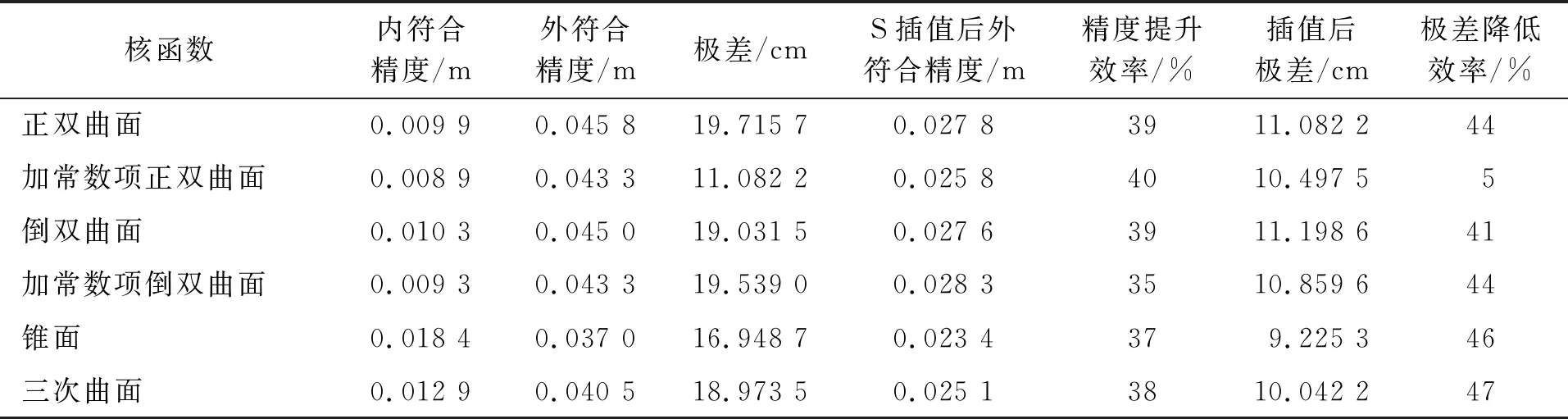
表2 六种多面函数拟合模型精度对比

基于多面函数的组合模型可以改正奇异点、收束残差曲线,达到提高外符合精度的目的。

3.3 基于神经网络组合模型

两种神经网络及其对应的组合模型残差曲线如图4所示。

图4 两种神经网络及组合模型残差

从图4可以看出,前半段BP神经网络波动较少曲线较为平滑,后半段均出现残差过大的奇异点,最大为14.65 cm,其出现的原因与测量误差、样本大小、训练次数和模型选择等有关。基于神经网络的组合模型残差曲线前半段趋势平缓,残差波动范围变小,后半段组合BP神经网络模型较组合RBF神经网络精度提升明显,具体精度对比如表3所示。

表3 两种神经网络及组合模型残差精度对比

由表3知基于神经网络组合模型,外符合精度平均提升22.5%;极差平均降低28.5%。

4 结束语

本文通过实测数据对比分析了3种方法下属的12类数学模型及其对应组合模型的拟合精度。其中,基于多面函数的组合模型精度提升效率最高,均能达到38%左右,对残差的收束情况较好,并对奇异点具有较好的改正效果;基于神经网络的组合模型次之,有22.5%左右的提升效率;基于多项式曲面的组合模型效果较弱,平均 8%左右的提升效率,且有个别残差改正过大情况。

结果表明:基于两步Shepard插值思想的组合模型特别是基于多面函数和神经网络的组合模型,在已知点较少的情况下,拟合精度较基础模型高,并具有减弱奇异点影响、平滑残差曲线的效果。可以得出,在已知点较少的情况下构建局部似大地水准面,此方法较单一拟合模型具有更高的拟合精度,但因数据量的原因,其普遍适用性有待进一步论证。