基于小波域三重MRF分割算法的遥感图像分割分析

张汉中

(广东省地质局第七地质大队, 广东 惠州 516008)

0 引言

2006年规划、2010年升空的高分卫星系统,可以实现亚米级的地面成像。且高分卫星属于可向民间提供全面宇航服务的民用卫星项目,允许民营机构随时下载高分卫星遥感图像,并按需进行分析[1]。但是,遥感图像受到大气条件(云层、雾霾等)、光照条件、曝光条件等影响,往往直接应用的价值较低[2]。所以,对遥感图像进行分析,使其清晰度提升且在不同区域实现图像分割域的补拍和替换操作。遥感图像的后期处理工作,主要分为图像的分割标记及曲线拟合分析[3]。

国内有关该领域的研究较为少见,国外相关研究基本集中在卫星图像图元分割和图像处理两个领域,其图元分割算法主要集中在马尔科夫随机场模型(Markov Random Field，MRF)分割算法的变形,而图像处理方面使用的模型众多。本文计划使用的小波域算法在国外相关研究中也有报道[4]。

MRF分割算法是在空间尺度对图像进行寻址分析的算法,通过仿真拍摄点的移动速度矢量,对空间尺度下的遥感图像进行标记和划分,特别是运动网格区域与静止网格区域间的相互作用比较微弱时,可以使用MRF 模型进行计算。小波域分析算法是一种基于低信噪比数据的抗干扰算法,通过小波域分析算法,可以让数据中噪声干扰得到有效压制,在卫星遥感图像的分析任务中,小波域算法可以实现对各种干扰条件造成的图像质量扰动的排除[5]。

本文拟使用三重MRF分割算法,属于MRF算法的一种变形形式,拟使用的图像处理算法为小波域图像处理算法。

1 小波域三重MRF分割算法的数学原理

1.1 基于MRF分割算法的遥感图像处理

构建图像的邻域系统,即在尺度为S×S的二维网格上定义一个L子集见式(1):

∂={∂(i,j):(i,j)∈S×S,∂(k,l)⊂S×S}

(1)

式中，针对所有的(i,j)∈∂(k,l)∪∂(i,j)均满足(i,j)∉∂(i,j),且当(k,l)∈∂(i,j)时,满足(i,j)∈∂(k,l)。即∂(i,j)为二维网格S×S上的邻域系统L,如图1所示。

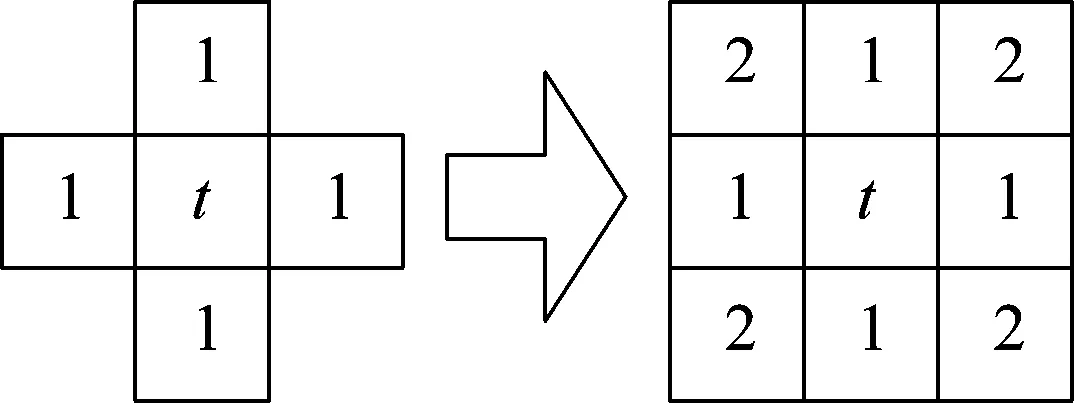
图1 邻域系统示意图

图1中,左图是MRF的一阶邻域系统,右图为MRF的二阶邻域系统。t为前文所述的图像集∂(i,j)。

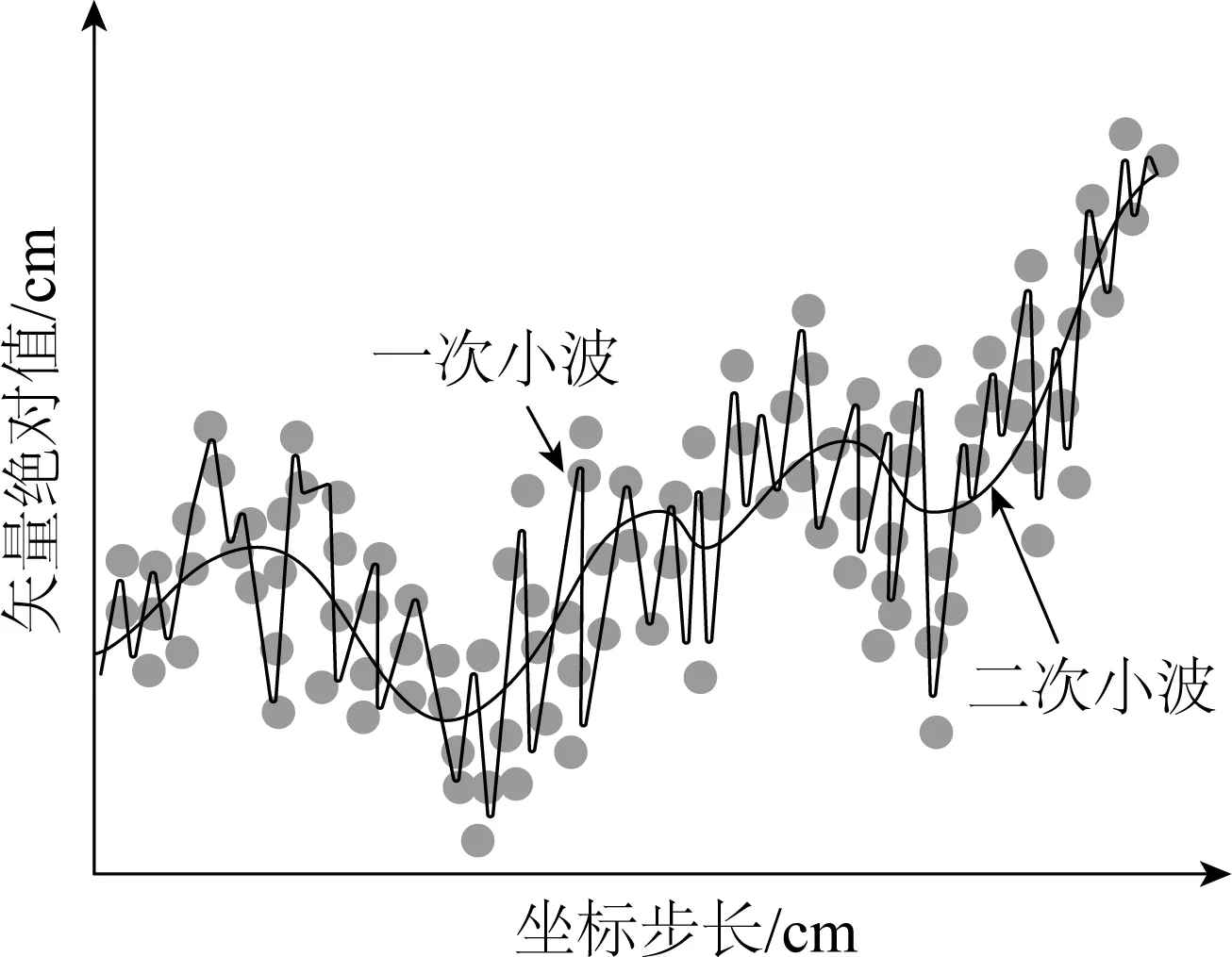
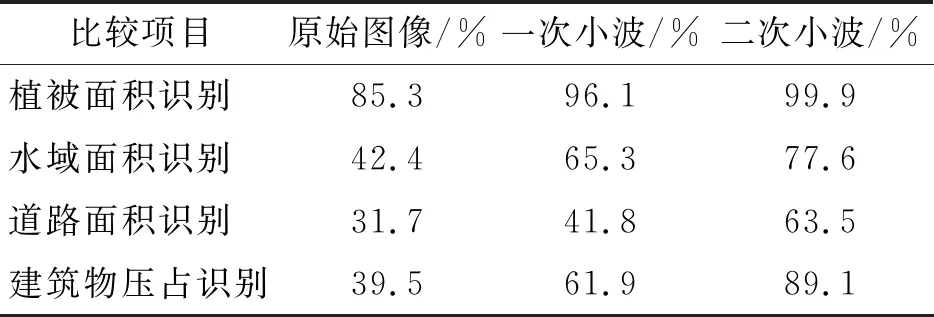
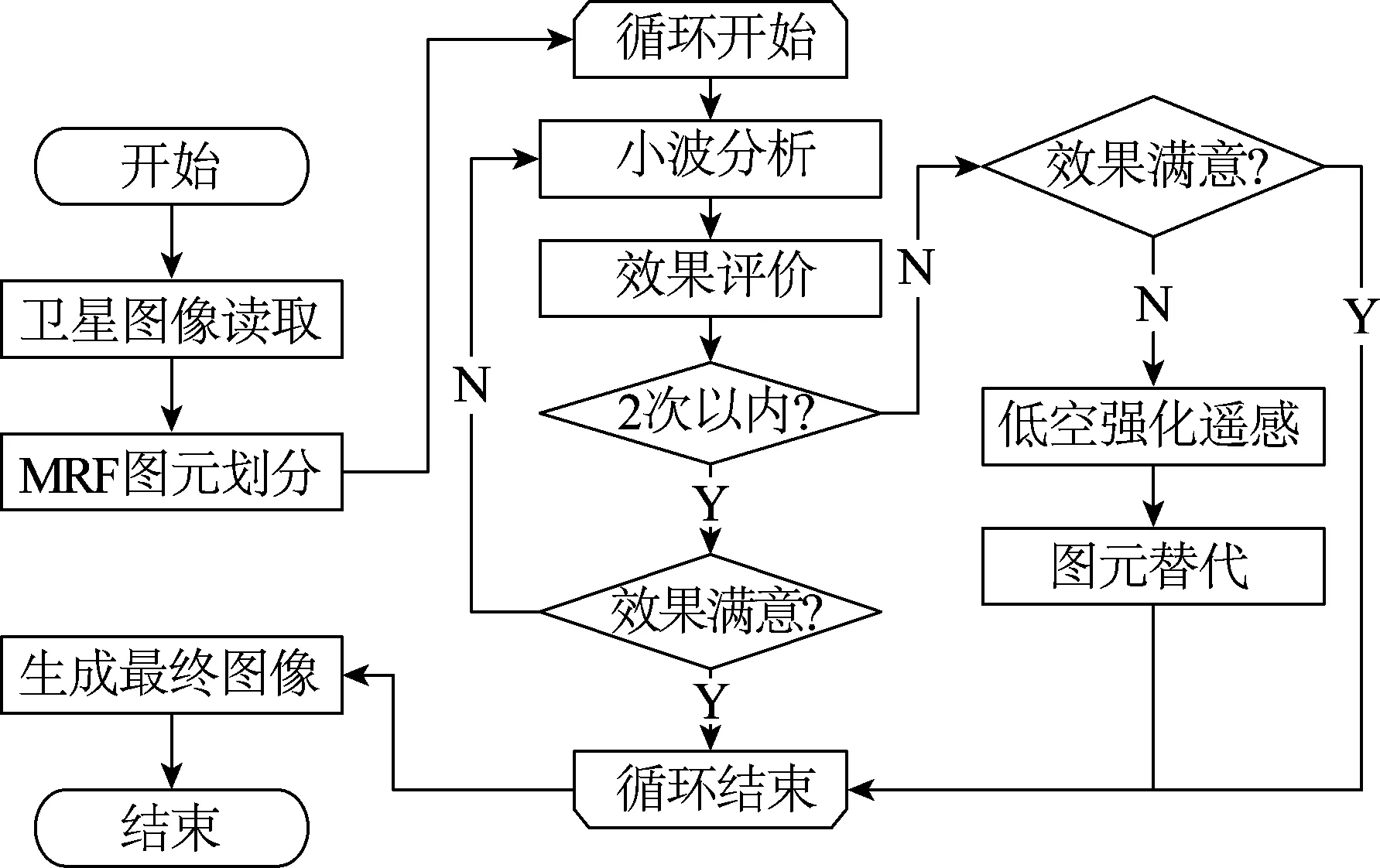
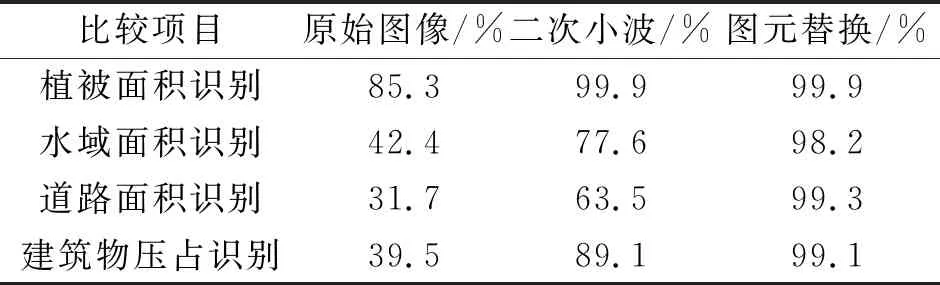
一阶邻域系统下,如果正整数集合n下,t0,t1,…,tn∈T,且t0

P{ε(tn)≤y|ε(tn-1)=xn-1,ε(tn-2)=

xn-2,…,ε(t0)=x0}=P{ε(tn)≤

y|ε(tn-1)=xn-1}

(2)

式中，当P对所有的ε(tn)成立时,则ε(t),t∈T为MRF的随机过程。

在上述MRF随机过程的基础上构建Ising模型,该模型假定在有限图元上每个点仅有2个取值,那么在上述二维网格L的MRF随机场X的空间状态可以表示为K={-1,+1},一阶邻域系统下,构建其Ising一元能量函数如公式(3)所示，二元能量函数如公式(4)所示:

V1(xs1=k)=αk,k∈{-1,+1}

(3)

(4)

公式(3)及公式(4)中，xs1,xs2分别为像素位置s1及s2的标号值,且满足s2∈∂(s1)；αk,β为其一元能量赋值和二元能量赋值,其逻辑关系见式(5):

(5)

式中，C属于集合{0,1}，即Vc根据数据状态符合式(1)中V1表达方式或式(4)中V2表达方式；其他所有数学符号如之前公式。将赋能函数与随机函数相结合,可以得到公式(6):

(6)

式中，所有数学符号如之前公式。

综上,MRF的本质过程是在遥感时序图像上进行进一步图元划分并利用一定规则(本文采用Ising模型规则)进行图元赋值。经过图元赋值的MRF划分图元,即可进行进一步的图像质量分析和图像质量加强处理。

1.2 基于小波域分析的图元质量加强算法

卫星图像虽然可以实现可见光条件下的亚米级分辨率,但其实际图像受到可见光的限制,仍难以排除云层、雾霾、光影、大气密度变化等对图像质量的干扰。此时,对图像质量进行分析,高保真需求下提取图像特征,成为其图元质量加强算法的核心需求[6]。

与常规RGB(Red Green Blue Mode)函数不同,卫星的可见光图像一般采用多个高穿透性波长的图像叠加,如400，680，750，2 500 nm等波长,而人眼的光锥细胞采集波长为490，570，630 nm。所以,卫星图像本身在可见光整合短红外波长体系下获得的相应图像与实际肉眼感知色彩之间存在一定的差异性。卫星可见光图像的采集波普显著宽于肉眼视锥细胞采集波普[7-8]。后续处理中,将卫星图像的等波长灰度图像针对人眼采集波长进行等效投影,最终获得卫星图像的颜色值,即卫星图像最终的像素存储格式仍为RGB格式,即使用3个长整形变量存储3个通道的灰度图像,进而使用RGB输出模式进行解释输出。

所以,对点阵的图像按照各自通道提取后,形成可进行小波域分析的图元信息。其小波分析基函数见式(7):

(7)

式中，p(y)属于时域下的多项式系数控制函数;m0(ω)属于变换控制过程。其中p(y)的表达式可以写作公式(8):

(8)

式中，C为多项式系数;k为控制变量;N为像素阵列总计数。

m0(ω)的表达式写做公式(9):

(9)

式中，-jkω为小波变换的傅里叶系数;k为控制变量;N为像素阵列总计数。

经过基于图元域条件下的小波变换,可以得到图元RGB参数下各通道信息的小波域优化结果。

2 个案条件下的模型应用及效果分析

2.1 个案基本情况

某山区规划工作中,使用高分五号卫星数据作为规划测量参考数据,规划区东西长5 km，南北长3 km,规划面积合计15 km2,规划区内最低海拔575 m,最高海拔1 394 m,区域内河道众多,山区植被覆盖茂盛。该区域遥感图雾气影响较重,区域内图像对比度较低,山势、河道水面、道路及相关植被和地表附属物的细节展示不明显[9]。所以,有必要使用上述小波域三重MRF分割算法进行图像信息加强处理。经过MRF图元提取后,对图元信息进行线性提取,并对其进行特征函数提取,可以得到图2结果。

图2 特征函数提取结果示意图

经过一次小波域分析后,其趋势特征仍不显著,信噪比仍较低,但经过二次小波分析后,图像的函数特征得以较充分展现。其实际处理效果详见图3。

图3 两次小波分析后的效果比较图

图3(a)为第一次小波分析后的图像结果,图3(b)为第二次小波分析后的图像效果。肉眼观察下,图3(b)的图像解析度显著优于图3(a)[10]。

2.2 小波域三重MRF分割算法在个案中的意义

参照上述个案中的实际图像处理效果,使用小波域三重MRF分割算法,在对图元进行充分分割的前提下,使用小波域算法对图强进行充分加强,可以在原始卫星图像资源中,实现对卫星图像信息的有效提取。对比原始图像、一次小波分析、二次小波分析的实际机器读图识别率,可以得到以下对比结果,如表1所示。

表1 机器读图的识别率比较表(原始图像)

可以看到,经过本文设计的小波域三重MRF分割算法对卫星图像处理后,基于高分卫星工具包提供的图像信息识别比率,在植被、水域、道路、建筑物等方面均有显著提升。特别是对植被的识别率已经达到了99.9%,但对道路、水面等的识别效率仍有待于提升。分析其原因,主要来自在植被发育茂盛的本文个案区域,水域与道路等被乔木植被的遮挡效应较为显著,即便有效提升了图像的解析度,该遮挡效果仍无法避免[11]。

MRF条件下,可以使用其他卫星数据根据图元标记进行替换,甚至可以使用飞机遥感数据和无人机超低空数据进行图元替换。其工作流如图4所示。

注：N表示否；Y表示是。

图4中,超过二次小波分析仍不能达到图像识别率的,进行低空强化遥感拍摄,并根据低空强化遥感的MRF图元分割结果,与卫星图像的MRF图元进行替换合并,以实现更高的图像识别率。经过低空强化遥感后的数据识别率,详见表2。

表2 机器读图的识别率比较表(图元替换)

表2中,使用无人机超低空遥感后,将其MRF分割图元域卫星图像的MRF低质量图元进行替换,从而再次使用工作流进行数据分析,最终交由高分卫星工具包软件进行图像识别,发现经过图元替换的识别率,除水域识别为98.2%略小于99%外,其他识别项目(植被、道路、建筑物)的识别率均达到了99%以上。可见该分析模型不仅对既得卫星图像的分析有积极意义,对卫星遥感与其他遥感方式的整合过程,也有显著的工程实践意义。

3 结束语

该模型的核心创新点在于,将卫星遥感图像的图元划分进行充分精细化,使卫星遥感图像可以划分成独立且不相交的图元并对其进行逐一操作,且可以通过小波域图像分析法,对图像特征进行有效提取,并对提取的图像特征进行充分强化。在无法达到图像特征强化需求的图元中,使用低空强化遥感的方式,对其进行补充测量。当前技术条件下,卫星遥感、航拍遥感、无人机摄影遥感等可以在MRF图元序列下进行有效整合。即航空航天技术在对规划测量、工程测量、施工测量、验收测量的全工程周期测量工作中,可以在MRF模型的支持下,实现无缝整合。MRF模型不仅对图像的划分过程实现无缝拼接,也可以在测量流程管理领域实现流程的无缝拼接。