基于局部能量与NSCT的红外与可见光图像融合
2021-07-28路黎明
路黎明
(安徽理工大学计算机科学与工程学院,安徽淮南 232000)
0 引言
图像融合是一种图像增强技术,它是将多个不同传感器所获取的同一场景图像融合成一幅新的图像,融合后的图像结合了源图像中的优势,得到了一张更清晰的图像,消除了源图像中的冗余信息,使源图像中的细节更加丰富[1]。目前图像融合技术的应用日益广泛,该领域已成为当今研究热点之一。图像融合技术已经渗透到各个领域中,例如遥感、军事、医学等方面。
红外与可见光图像的融合是图像融合领域研究热点之一,红外传感器可以对物体进行热辐射成像,并且能够探测出场景中热目标,红外传感器可以全天工作。但是红外传感器捕获的图像比较模糊,图像分辨率不够高;而可见光传感器所捕获的图像比红外传感器所捕获的图像拥有较更高的分辨率与对比度,图像中的信息比较丰富。因此,红外与可见光图像的融合比单传感器所捕获的图像细节信息更加丰富,并且存在几乎所有对象的固有特征。红外与可见光图像融合所得到的图像具有高空间分辨率和丰富的细节,更适合人类视觉感知。
1 图像融合的三个层次
图像融合可分为三个层次:像素级融合、特征级融合和决策级融合。三个融合层次中最低的是像素级融合,像素级融合是直接对源图像的灰度数据进行处理操作。对源图像处理后,会得到比源图像拥有更多细节信息,如边缘和纹理信息,方便对图像后续的处理和分析,像素级融合方法可以最大程度上保留源图像的细节信息,因此,经过像素级融合处理后所得到的图片会拥有比源图像更多的细节信息和内容。由于需要对源图像的灰度数据进行直接处理,像素级融合对计算机的计算性能要求较高,且需要较长的处理时间,这也是像素级融合的局限性。像素级融合可划分为基于空间域的融合和基于变换域的融合,主要算法包括:主成分分析法、拉普拉斯金字塔变换法、小波变换法、Contourlet变换法、非下采样轮廓波变换法等。
特征级融合为三个融合层次的中间层次,特征级融合需要先从源图像提取边缘、纹理等重要特征信息,然后再对所提取到的特征信息进行分析和处理,最终根据对这些特征信息的处理就可以得到融合图像所需的特征信息。相对于像素级融合,特征及融合仅需处理少量的数据,所需要的处理时间会大大缩短,得到融合图像的速度也有提升;但特征级融合依靠的是提取的特征信息,信息提取的质量会影响融合图像,因此融合后的图像相比较源图像细节往往信息不够丰富,丢失信息较多。
三个融合层次中的最高层次是决策级融合,它是对特征级融合所提取的特征信息进行进一步的处理,处理过程需要一系列的判定准则和决策分类,基于这些准则和决策输出一个效果最优的结果。决策级图像融合的计算量相比决策级融合进一步的减少, 是三个层次中计算量最小的融合方法;但是细节信息丢失也较严重。
2 基于多尺度变换的图像融合算法
多尺度变换由于具有良好的时域与频域局域性,已被国内外许多专家广泛应用于图像融合领域。多尺度变换可以将原始图像分解为不同尺度的分量,其中每个分量代表每个尺度的子图像;多项研究表明多尺度变换具有与人类的视觉特征一致的特性,而且这种特性可以使融合图像拥有优秀的视觉效果。基于多尺度变换的图像融合方法通常包括三个步骤,首先将每个源图像进行多尺度分解,然后根据给定的融合规则对分解得到的子带进行融合,最后使用相应的逆多尺度变换获取融合图像[2]。基于多尺度变换的融合方法关键在于融合规则的选择。经典的多尺度变换方法有金字塔变换、小波变换、Contourlet变换、NSCT等。但金字塔变换容易造成局部模糊现象,小波变换空间细节信息增强能力稍显不足,Contourlet变换缺乏平移不变性且有明显的伪G i b b s效应,N S C T继承了Contourlet变换的优点,并且具有平移不变性,是图像融合较为有效的分析工具[3]。
2.1 离散小波变换
小波变换是由傅里叶变换改进而来的,克服了傅里叶变换不具有时间频率的局部化分析能力的缺点。小波变换现在已经被广泛应用于图像融合领域,它将源图像在各种方向上进行分解,并进行时域和频域分析。小波变换可分为连续小波变换(CWT)和离散小波变换(DWT),由于连续小波变换只适用于处理连续的信号,在处理离散的信号时,就需要使用离散小波变换,相对于连续小波变换,离散小波变换可以减少数据信息量,更利于数据压缩的实现,提高了应用效率。
2.2 Contourlet变换
Contourlet变换是由M.N.Do等人于2002年提出的一种能够更好表示二维信号的方法,相对于小波变换,它不仅具有小波变换的多分辨率和时频局部的特性,还具有多方向性和各向异性,可以很好的表示图像边缘轮廓曲线信息。Contourlet是用金字塔方向滤波器(PDFB)将源图像分解为不同尺度下的方向子带,PDFB是由一个拉普拉斯金字塔滤波器和一个方向滤波器组组成的,首先将源图像使用拉普拉斯金字塔变换进行多尺度金字塔分解,以捕获点奇异性,然后再由方向滤波器组将分布不同方向上的奇异点合成不同的系数。实验证明,Contourlet变换在图像降噪、纹理、形状的特征提取方面的性能比小波变换有了明显的提高。
2.3 非下采样轮廓波变换(NSCT)
由于Contourlet变换过程中需要进行下采样和上采样,令其缺乏平移不变性,且有明显的Gibbs效应。为了克服Contourlet变换这些缺点,Arthur L.Cunhua提出了NSCT,与Contourlet变换相比,NSCT不仅继承了多分辨率、时频局部化、良好的方向选择性和各向异性的特点,由于取消了对图像的下采样,NSCT还具备平移不变性。NSCT由非下采样塔式滤波器组(Nonsubsampled pyramid filter bank,NSPFB)和非下采样方向滤波器组(Nonsubsampled directional filter bank,NSDFB)组成。NSPFB用于对源图像进行多分辨率分解,NSDFB用于对源图像进行多方向的分解。图像经过M层分解可得到个高频子带和1个低频子带,得到的子带大小与源图像大小一致[4]。NSCT分解过程如图1所示。
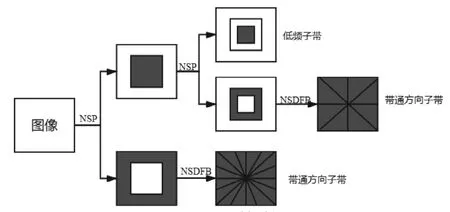
图1 NSCT分解过程Fig.1 NSCT decomposition process
3 本文融合方法
首先对源图像进行NSCT分解,得到低频子带和高频子带,低频子带采用基于局部能量的方法进行融合,高频子带采用绝对最大值的方法进行融合。
3.1 高频融合
高频子带表示图像的细节信息,如轮廓、和边缘细节等,由于图像细节特征比较显著,所以本文高频部分采取绝对最大值的方法进行融合。
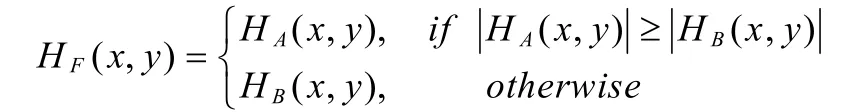
其中H F(x,y)、H A(x,y)与H B(x,y)分别表示融合后的图像、源图像A、源图像B在(,)x y处的高频分解系数。
3.2 低频融合
低频子带中包含着图像的轮廓信息,为了使融合后的图像的清晰度和对比度都有良好的表现,对低频子带采用局部能量方法进行融合,局部能量按照公式(1)计算。

其中LF(x,y)、L A(x,y)与L B(x,y)分别表示融合后的图像、源图像A、源图像B在(,)x y处的低频分解系数。
4 实验结果与分析
为了验证本文提出的方法有效性,选取了如图2所示的一组红外与可见光图像进行实验,实验环境为Matlab 2016,实验结果如下图所示。从视觉效果来看,DWT方法融合效果最差,出现了明显的块效应;而Contourlet方法和本文所提出的方法的视觉效果明显优于DWT方法。

图2 红外与可见光图像实验图Fig.2 Experimental picture of infrared and visible images
本文的客观指标采用信息熵(Information Entropy,IE)、标准差(Standard Deviation,SD)和互信息(Mutual Information,MI)来衡量融合图像的质量,IE反映的是图像的信息量,图像的IE越大,表示图像中包含的信息量越丰富;SD反映图像的对比度,SD越大,意味着图像的对比度越大;MI表示融合图像中包含源图像的信息量,MI值越大,表示融合图像继承了源图像信息越多[5]。从客观指标来看,本文算法在信息熵、标准差、互信息都比所对比的算法要好,因此融合图像在信息量、对比度等方面都优于对比算法,融合图像质量更好。如表1所示。
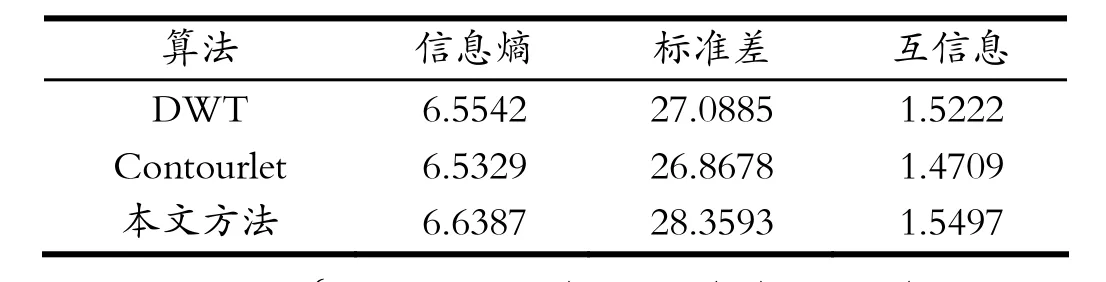
表1 几种方法融合结果的比较Tab.1 Comparison of fusion results of several methods
5 结论
本文提出了一种基于NSCT的红外与可见光图像融合方法,高频采用,低频采用局部能量的规则进行融合。对红外与可见光图像进行融合实验,并与方法进行主观与客观分析。实验结果表明,本文提出的算法更好的保留源图像的细节信息,融合效果优于方法。
