一个收敛无穷级数和的两种概率模型求解

舒洪铭 许昌林

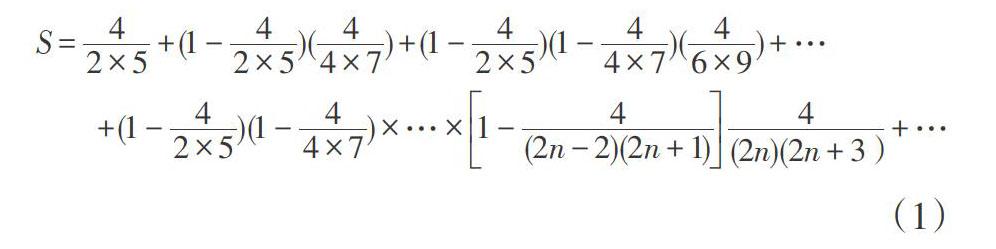
摘 要：对于收敛的无穷级数的求和有时候存在困难， 本文通过构造两种不同的概率模型， 将一个收敛的无穷级数求和问题转化为概率问题， 然后利用概率的公理化定义以及概率运算性质， 对复杂收敛无穷级数的和进行求解. 另外， 说明了对于同一个收敛无穷级数的求和， 可能存在着多种概率模型， 从而丰富了收敛级数的求和方法.

关键字：级数求和; 概率模型; 概率运算性质.

中图分类号O173    文献标识码 A

一、 引言

目前， 对于收敛无穷级数的求和方法有很多， 比如定義法、构造关系式法、求幂级数的和函数法、幂级数展开式等方法^[1][2][3]. 当然除了这些级数求和方法以外， 对一些复杂收敛无穷级数的求和问题， 利用上述基础方法求解起来比较困难， 此时通过构造一些适当的概率模型进行求解收敛无穷级数的和是一种比较好的途径^[4]. 为此， 本文针对一个复杂收敛正项级数的和的求解问题， 适当构造了两种概率模型进行求解， 不仅解决了特殊无穷级数的求和问题， 还进一步说明了对于一些收敛级数的求和问题来说， 可能同时存在着多种概率模型.

比如针对下列正向无穷级数

的求和问题. 由正项级数收敛的判别准则^[6]可知（1）式收敛. 为了求解无穷级数（1）式的和， 下面通过构造适当的概率模型来对其进行求解.

二、 无穷级数和的第一种概率模型求解

概率模型1：设有两个一样的盒子， 第一个盒子有1个红球、1个白球， 第二个盒子有4个红球、1个白球， 小球除了颜色不同， 其余特征均相同. 现在有放回的从两个盒子中各取1个小球， 若取出的2个小球均为红球， 则试验成功， 停止试验; 反之试验失败， 此时再向两个盒子中分别各加入2个白球， 重复上述试验， 直到试验成功. 求该试验成功的概率.

• 无穷级数和的第二种概率模型求解

对于（1）式收敛级数的求和， 还可以构造其他概率模型进行求解， 如此可以构造下面的概率模型进行求解.

概率模型2： 设有两个一样的盒子， 第一个盒子有2个红球、0个白球， 第二个盒子有2个红球、3个白球， 小球除了颜色不同， 其余特征均相同. 重复模型1的试验步骤， 求该试验成功的概率.

四、 总结

本文对一个复杂收敛的无穷级数和的求解问题， 从构造不同概率模型角度出发， 将复杂求和问题转化为利用概率论预算性质进行求解， 计算过程简单明了， 简化了求和复杂程度， 同时也降低了求解难度， 这为收敛的无穷级数的求和问题提供了不同的途径. 同时， 也能看出， 对于同一个收敛的无穷级数， 可以构造不同的概率模型进行求解. 可见， 运用概率模型求解无穷级数和的灵活性.

参考文献

[1]吕海翠， 宋佳， 王艳丽. 高等数学中一类幂级数求和函数的重要方法[J]. 数学学习与研究， 2020（12）：142-143.

[2]郑丽娜. 一道数项级数求和问题解法探讨[J]. 科技资讯，  2020， 18（02）：223-224.

[3]由悦. 级数求和的常见方法[J]. 数学学习与研究， 2018（19）：6.

[4]马醒花， 张成虎. 两个级数求和问题的概率模型[J]. 高等数学研究， 2014， 17（01）：45-46.

[5]茆诗松， 程依明， 濮小龙. 概率论与数理统计教程（第3版）[M]. 北京：高等教育出版社， 2019.

[6]华东师范大学数学科学学院. 数学分析（第五版）[M]. 北京： 高等教育出版社， 2019.