FeCu模型合金中Cu析出物导致硬化的位错动力学研究

2021-07-27滕明航贺新福豆艳坤王东杰贾丽霞

原子能科学技术 2021年7期

滕明航，贺新福，豆艳坤，王东杰，贾丽霞

(中国原子能科学研究院反应堆工程技术研究所，北京 102413)

压力容器(RPV)是压水反应堆中不可更换的关键部件，RPV钢(一般为铁素体钢)在服役过程中经高能中子轰击会导致缺陷产生乃至微结构演化，如形成位错环、析出物等辐照缺陷，这些辐照缺陷阻碍位错运动，从而导致硬化和脆化，是影响反应堆安全性和经济性的关键因素之一。研究表明，低铜RPV钢(如A508-Ⅲ钢)中引起辐照硬化和脆化的缺陷主要为尺寸很小(平均半径<2 nm)而数密度很高(～1024m-3)的溶质-缺陷团簇[1-2]，团簇的主要成分是Cu、Ni、Mn和Si等。如此小的缺陷很难利用实验手段进行精准表征，从而使得建立显微组织与宏观性能间的关系变得非常困难。

基于位错与缺陷相互作用的位错动力学(DD)方法，通过统计分析各种类型/尺寸的缺陷对位错的钉扎作用，可建立微结构信息(障碍物的尺寸和数密度)与力学性能(如临界分切应力、硬度、屈服强度)之间的关联关系，因此DD方法在材料辐照硬化研究中发挥着非常重要的作用，有助于加深人们对材料辐照硬化机制的理解，Ghoniem、Marian和吴恺慆等[3-5]深入系统地介绍了辐照硬化的DD研究进展，包括DD基本原理及其在辐照损伤领域的应用等。

国际上针对RPV钢及FeCu模型合金辐照硬化的DD模拟开展了广泛的研究，如欧盟开发的RPV钢辐照脆化多尺度模拟软件系统RPV-1[6]和RPV-2[7]中，均采用Foreman和Makin型DD方法[8]建立辐照微结构与硬化之间的关联关系，分析了辐照导致析出物和位错环等对辐照硬化的贡献，其中辐照缺陷对位错的钉扎力由分子静力学(MS)计算并拟合获得，形成钉扎力数据库[9]；美国正在开发的RPV钢辐照脆化多尺度模拟Grizzly软件[10]中，也是通过DD建立位错环和析出物等辐照微结构与宏观性能之间的关系。与欧盟RPV系列软件不同的是，Grizzly软件中的钉扎力是通过分子动力学(MD)计算位错与缺陷间的相互作用，获得临界分切应力，进而得到辐照缺陷的钉扎力。Monnet[11]基于DD方法，系统分析了碳化物、位错网络以及辐照微结构(位错环、空洞、析出物等)对硬化的影响，同时分析了不同滑移系对位错-缺陷相互作用的影响机制。中国原子能科学研究院材料辐照效应团队(MIET)针对RPV钢和低活性铁素体/马氏体(RAFM)钢中位错与缺陷相互作用开展了较为深入的研究，分析了位错环[12-14]、溶质缀饰位错环[15]和析出物[16-19]等对位错的阻碍作用，在此基础上开发了具有自主知识产权的DD程序。

引起材料硬化的因素/机制主要有固溶强化、位错网络导致硬化、Hall-Petch效应和辐照缺陷导致的硬化等，考虑到低铜RPV钢在辐照过程中溶质含量较低且辐照损伤剂量较低，辐照前后固溶强化、位错网络和Hall-Petch效应导致的硬化变化不大，因此一般认为导致RPV钢辐照硬化的主要因素是析出物。因其成分与结构难以精确表征，难以直接建立模型，故先以热老化产生的Cu析出物为研究对象，建立Cu析出物的脱钉扎判据与DD模型，为后续RPV钢辐照下产生的析出物的硬化作用研究奠定基础。本文主要研究FeCu模型合金中Cu析出物导致的硬化机理，通过MD研究位错与缺陷之间的相互作用机理，计算获得缺陷的钉扎力，然后基于自主开发的DD程序计算Cu析出物引起的屈服应力增量，并与典型文献实验结果进行对比；最后对比分析不同方法(MS、MD)计算获得的钉扎力和脱钉扎临界角θc等敏感参数对模拟结果的影响。

1 模拟方法

1.1 位错动力学

本文采用DD程序计算单晶内辐照缺陷引起的临界切应力增量，通过在模拟盒中随机分布一定数量的缺陷，模拟单根位错滑移并克服所有缺陷(位错不能离开滑移面，即没有交叉滑移和攀升)，计算克服每个缺陷所需的切应力，该过程中的最大切应力即为缺陷阻碍位错移动的临界切应力(CRSS)。为获得多晶体中辐照缺陷所引起的硬化，可将CRSS与泰勒系数相乘，即获得屈服应力增量Δσy。

在应力场σ的作用下，位错受缺陷钉扎时的构型如图1所示，此时位错线受到驱使其向前滑移的线张力T以及阻碍其滑移的缺陷钉扎力Ff的共同作用。随着应力逐渐增大，施加到位错上的线张力增大，当线张力合力大于缺陷的钉扎力时，缺陷被克服；同时位错线也不断弯曲，当位错线形成Frank-Read型不稳定结构[20]或3个连续缺陷间的夹角小于一定的角度时，缺陷两边的位错线会连接并通过缺陷，在缺陷周围留下1个位错环。对应上述情形，当满足以下3个条件中的任何1个时，即可认为位错脱钉扎：1) 力判据，线张力合力F大于缺陷的钉扎力Ff；2) 角判据，缺陷两侧位错线间夹角θ小于设定的临界值θc；3) 弧判据，位错弧段的曲率半径小于缺陷间隔离L的1/2。

图1 位错受缺陷钉扎时的构型及受力分析Fig.1 Configuration and force of dislocation pinned by defect

DD程序计算流程如图2所示，其关键的输入参数为缺陷的尺寸、数密度以及钉扎力。

图2 DD程序流程框图Fig.2 Flow chart of DD

为避免因缺陷数量太少引起的误差，本文计算过程中通过调整模拟盒的尺寸，确保模拟盒中的缺陷数不少于5 000个(根据前期经验，当模拟盒中缺陷数量不少于5 000时，保持缺陷数密度不变，增加缺陷数量对最终计算结果基本无影响)；同时为减少在模拟盒中随机放入缺陷所引起的误差，每个算例进行5次随机数不同的计算，以减小随机性误差的影响。本文模拟参数列于表1。

表1 DD模拟参数Table 1 Material parameter for DD simulation

1.2 缺陷钉扎力计算

如前文所述，缺陷钉扎力可利用MS或MD方法计算获得，然后通过拟合获得不同半径缺陷的钉扎力。MS计算的钉扎力Ff(eV/nm)与半径为r(nm)的障碍物之间的关系[9]如下：

Ff=7.54r1.17

(1)

1.3 位错线张力计算

线张力T选取与缺陷半径相关的变张力模型[27]计算：

(2)

式中：f(ω)为方向因子，对于螺位错该值取1，对于刃位错该值取1/(1-ν)；L为缺陷间的距离。

2 结果与讨论

2.1 MD计算Cu团簇的钉扎力

图3 MD和MS方法拟合所得富Cu析出物的钉扎力Fig.3 Pinning force of copper-rich precipitateadapted by MD and MS methods

利用1.2节的MD方法，模拟了300 K时位错与不同尺寸共格Cu团簇的相互作用过程，分析了不同相互作用位置对CRSS的影响，结果如图3所示。图中同时给出了Osetsky、Bacon和Terentyev等[28-31]模拟的刃位错与Cu团簇相互作用的数据。由图3可看出，MD计算获得的钉扎力随团簇尺寸的增加而增大，其变化趋势与文献结果一致，同时可看出，当析出物半径小于0.5 nm时，其钉扎力随半径的减小而迅速下降，这主要是因为随着析出物尺寸的减小及温度对位错运动的激活作用，析出物阻碍位错运动的能力明显下降。基于本文MD计算结果以及文献结果，对析出物的钉扎力进行了拟合，如图3所示。

Jumel等[9]基于MS计算获得的钉扎力及其拟合公式如式(3)所示。对比图3中MS/MD钉扎力公式的拟合结果，可看出当析出物尺寸较小(半径小于1 nm)时，MS和MD计算获得的钉扎力接近；而随着析出物尺寸的增加，两者间的差距增大，这主要是因为MS计算是在0 K下进行的，未考虑温度的热激活作用。

Ff=4.63r0.88

(3)

2.2 临界角θc的选取

临界角θc是DD模拟的关键判据之一，针对富Cu团簇钉扎位错时的临界角θc，国际上开展了大量的研究。θc的确定主要有两种方法：一种是通过实验结果结合理论模型反推，如Deschamps通过Fe-0.8%Cu模型合金在500 ℃时效不同时间的硬度变化以及微观分析结果，结合Russell-Brown模型反推获得了富Cu析出物的临界角θc∈[120°，150°][32]；另一种是利用MD模拟位错与析出物的相互作用，通过脱钉扎时的构型确定θc[33]。Shim等[33]利用MD计算了螺位错与不同尺寸(直径为1～4 nm)共格Cu析出物相互作用过程，分析了析出物尺寸对θc的影响，发现析出物直径为1.5～2.5 nm时，θc约为160°～170°；随着析出物尺寸增加至3.5 nm，θc将变为约110°。本文MD计算结果及前期结果也表明，位错与不同半径的析出物在不同位置发生相互作用时，θc皆小于160°。因此在后续DD模拟时，选取θc为100°～160°进行计算和分析。

2.3 DD模拟结果与实验结果对比

为验证本文DD模型及程序的正确性，选取5组有代表性的时效不同时间的FeCu模型合金作为模拟对象，其中Deschamps等[32]对Fe-0.8%Cu模型合金在500 ℃下时效了300 h，利用小角中子散射(SANS)技术分析了时效不同时间后析出物的尺寸(直径d)和数密度N，并测量了对应的屈服强度；Goodman等[34]和Mathon[35]分析了500 ℃时效Fe-1.5%Cu模型合金的析出物信息和屈服强度及维氏硬度变化。此外，Jumel、Ahlawat和Schober等[9,36-37]皆开展了FeCu合金在500 ℃时效后的微结构表征以及力学性能测试。上述实验测量的析出物尺寸和数密度示于图4，可见，析出物的尺寸和数密度随时效时间的变化具有一致的趋势。

上述文献在进行时效不同时间后的力学测量时，部分文献测量的是维氏硬度增量ΔHv，为统一，本文将上述实验中维氏硬度变化量ΔHv与屈服强度增量Δσy进行了转化，转化关系为：

Δσy=(2.5～2.7)ΔHv

(4)

虽然各组实验的析出物半径和数密度随时间变化的趋势基本一致，但力学性能测试结果却表现出一定的差异性，尤其是Ahlawat[36]和Schober等[37]各有2个实验数据点(图5中圆圈所示)与其他实验结果趋势不一致，这可能是因为材料成分以及测试过程中的误差所致，因此在后续计算中，上述4个点不进行模拟结果与实验结果的对比。

总体上，屈服强度增量随时效时间的增加而降低，并与(Nd)1/2近似呈线性关系(满足弥散强化(DBH)模型Δσy∝(Nd)1/2)，但当(Nd)1/2>0.03 nm-1(对应于时效时间很短，主要是高密度小尺寸析出物)时，Δσy与(Nd)1/2间不再满足DBH模型。

基于表1中的材料参数以及上述实验测量获得的析出物尺寸及数密度信息，本文开展了析出物导致硬化的DD模拟。为进行对比分析，模拟时钉扎力分别采用MS和MD计算结果的拟合公式，临界角θc分别选取110°、130°、150°，结果如图6所示(实验结果为实心点，计算结果为空心点)。当θc=130°时，模拟结果与实验结果趋势一致，且当析出物半径大于2 nm时，MS钉扎力和MD钉扎力的计算结果基本一致。模拟结果与实验结果存在差异的区域主要是小析出物(半径小于1 nm)，这主要是因为小析出物的钉扎力(MS/MD计算结果)较小，而在实验过程中可能还存在其他引起硬化的因素。当析出物尺寸较大(半径>2 nm)时，基于MS钉扎力和MD钉扎力模拟获得的Δσy基本一致，而由2.1节可知，当析出物半径>1 nm时，MS钉扎力和MD钉扎力存在较大差异，为解释该现象，本文详细分析了DD模拟过程中各缺陷的脱钉扎过程。

图4 不同时效时间析出物半径和数密度演化趋势Fig.4 Evolution trend of radius and number density of copper rich precipitates with thermal aging time

图5 不同实验者获得的屈服强度与析出物半径和(Nd)1/2间关系的对比Fig.5 Comparison of relationship between yield strength obtained by different experimenters and precipitate radius and (Nd)1/2

由图6可见，随着θc取值的不同，计算结果之间也存在着较大的差异，θc=130°时模拟结果与实验结果相近。如2.2节所述，国际上针对Cu析出物的临界角θc开展了模拟计算以及实验结果反推，结合本文的模拟结果，可得出热时效Cu析出物的临界角θc取值约为130°。

图6 不同钉扎力公式和θc的Δσy热老化实验值与DD模拟值对比Fig.6 Comparison of DD simulation and mechanical testing with different pinning force and θc

为分析MS和MD计算钉扎力存在较大差异，但模拟获得的Δσy基本一致这个现象，本文详细分析了模拟过程中的脱钉扎过程，统计分析了每个缺陷脱钉扎时的位错线张力、临界角等参数，在此基础上统计了所有缺陷的脱钉扎判据占比，结果示于图7。本文仅对θc=130°时的脱钉扎判据占比进行分析。由图7b、e可知，当析出物半径较小(MS：≤1 nm；MD：≤1.2 nm)时，力判据占据主导地位(占比超过80%，甚至90%)，当析出物尺寸大于上述数值时，脱钉扎过程以角判据为主；对于本文所模拟的析出物尺寸范围(半径≤10 nm)，弧判据占比都非常小(不超过5%)。因此，虽然析出物半径>1 nm时，MS和MD计算钉扎力存在差异，但该尺寸下的脱钉扎判据主要为角判据，在脱钉扎过程中均未达到析出物最大的钉扎力就已脱钉扎，因此图6b所示的MS钉扎力和MD钉扎力模拟获得的Δσy基本一致是合理的。

本模拟共22个算例，自由度为21，选取80%置信水平，查表得c=1.323，得到MD钉扎力结果处理后的平均值为1.03、均方差为0.26，对应的置信区间为[0.69，1.37]；MS钉扎力结果处理后的平均值为0.99、均方差为0.29，对应的置信区间为[0.61，1.37]。图8为MS钉扎和MD钉扎两种方法置信区间的对比，可看出本文DD计算结果与实验结果吻合较好，且MS钉扎力结果的离散性更好。

MS钉扎力较MD钉扎力公式偏大的原因可能是MS方法未考虑热激活作用的影响。本文中Cu析出物的半径较大，整体上以角判据主导脱钉扎，热激活作用带来的偏差不大。下一步对小尺寸析出物的硬化作用研究时需着重考虑热激活作用的影响，可通过MD模拟结果评估热激活作用的系数，对MS钉扎力公式进行修正。MD钉扎力公式是利用刃位错-缺陷间相互作用的结果得到，而实际上主导RPV钢低温塑性行为的位错是螺位错。目前国际上使用MD方法研究刃位错的较多，而研究螺位错的较少，已有的研究结果表明二者与缺陷间的相互作用虽有不同但相差不大，本文暂用刃位错的MD结果进行计算，下一步将会构建螺位错与缺陷间作用的MD模型，深入研究缺陷对螺位错的阻碍作用。

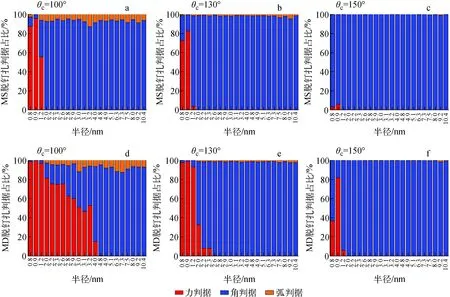
图7 不同钉扎力公式和θc的DD模拟结果中脱钉扎判据占比Fig.7 Proportion of unpinning criterion in DD simulation with different pinning force and θc

图8 不同钉扎力公式和θc的DD模拟值80%置信区间对比Fig.8 Confidence interval of 80% confidence of DD simulation with different pinning force and θc

2.4 θc敏感性分析

2.3节的计算结果表明，当临界角θc取130°时DD模拟结果与实验结果相近，且θc的取值变化对计算结果有较大的影响，因此本节将具体研究θc值变化对DD模拟结果的影响。

本文选取两个不同的析出物数密度(9.5×10-4nm-3和7×10-5nm-3)和半径(0.4～6.3 nm)及临界角(在175°～0°中选取20个节点)开展计算，结果如图9所示。由图9可见，析出物半径较小(<1 nm)时，θc<120°的任意取值对Δσy的计算结果基本无影响，表明角判据在此范围内不是主要的脱钉扎判据(与2.3节的结论一致)，统计分析发现上述条件下，力判据是主要的脱钉扎判据。当析出物半径大于3 nm时，角判据θc的取值对DD计算结果有较大的影响。