倒阶梯型变截面水平受荷桩数值模拟研究

谢 枫, 郑治祥, 王锦涛

(中国能源建设集团安徽省电力设计院有限公司，安徽 合肥 230601)

0 引 言

伴随着我国的经济发展，许多超高层建筑及交通干线的大跨度建筑拔地而起，对桩基的承载力也提出了更高的要求。为了满足桩基承载力，会增加相应的桩径与桩长，从而增加施工投入。倒阶梯型变截面桩在我国的建筑物中已有广泛应用，如广东九江大桥、江西湖口大桥、武汉天心州大桥等[1]。在工程实践中，绝大多数的桩在承受竖向荷载的同时，也承受一部分的水平荷载。相比较常规的等截面桩而言，变截面桩在承受剪应力时，剪应力呈现上大下小的特点，故利用桩受水平作用下的剪应力的特点，可既不减少水平承载力，又相应地节约材料和控制成本。因此，对倒阶梯形变截面桩分析与优化具有重要的理论和实践意义。

1 有限元计算方法简介

有限元方法是20世纪六七十年代发展起来的数值模拟方法。1960年Clough在处理平面弹性问题时，第一次提出并使用“有限元方法”的名称[2]。有限元解决问题的基本原理是将被研究的物体离散成有限个无限小的单元体，而对于每个小的单元体，用有限个确定参数来对其力学特性进行描述，根据弹塑性力学理论，将每个无限小的单元体的力学特性进行叠加，从而得到整体连续性的规律[3]。

2 数值模拟分析

2.1 基本假定

(1)桩体与土体皆采用六面体八节点的SOLID 45实体单元，桩体假设为理想弹性材料，土体假设为理想弹塑性材料。

(2)本构模型选用理想弹塑性的D-P准则。

(3)模拟桩与土的相互作用，需在桩土之间设置接触单元。定义桩体接触面为目标面，选用TARGE 170目标单元;定义土体为接触面，选用CONTA 173接触单元。

(4)土体假设为均质、各向同性。

(5)在桩顶面覆盖3D结构表面效应单元SURF 154，用于施加水平荷载。

2.2 有限元模型建立

2.2.1 模型尺寸的选取

为对比分析等截面桩与变截面桩的水平承载能力，选取灌注桩标准桩的直径d为0.3 m，扩大段直径为2d(即0.6 m)，桩身长度为20d(即6 m),具体模型的示意图如图1所示。

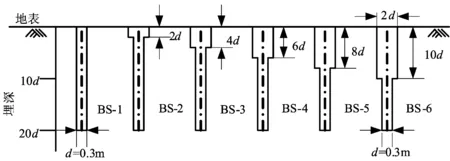
图1 桩体模型示意图

2.2.2 材料参数的选取

本文数值模拟采用的参数主要为弹性模量E、泊松比v、黏聚力C和摩擦角，涉及桩土接触问题，还有摩擦系数μ，取值为0.25。具体材料参数取值见表1。

表1 材料参数取值

2.2.3 模型网格划分

为了减小计算量，本次数值模拟采用二分之一模型，等直径桩周围土体影响范围选定为15d(即4.5 m)，底部土体影响范围选定为5d(即1.5 m)，变截面桩桩周土体和桩底土体的影响范围根据桩变截面扩大段直径确定影响范围，分别为30d(即3 m)、10d(即3 m)。模型采用扫掠网格划分的方式，等截面桩与变截面桩网格划分如图2所示。

图2 桩划分网格示意图

2.3 模型约束与加载

因选用二分之一模型进行模拟，故对桩体和土体截面处施加对称约束，对土体模型底面施加Z方向的位移约束，对土体模型周围施加X、Y方向的位移约束。加载时对桩土模型施加重力荷载，对桩基顶面施加X方向的水平荷载时，选用表面效应单元施加。

2.4 数值模拟结果及分析

2.4.1 荷载-位移曲线对比

不同试验桩的荷载-位移曲线如图3所示。

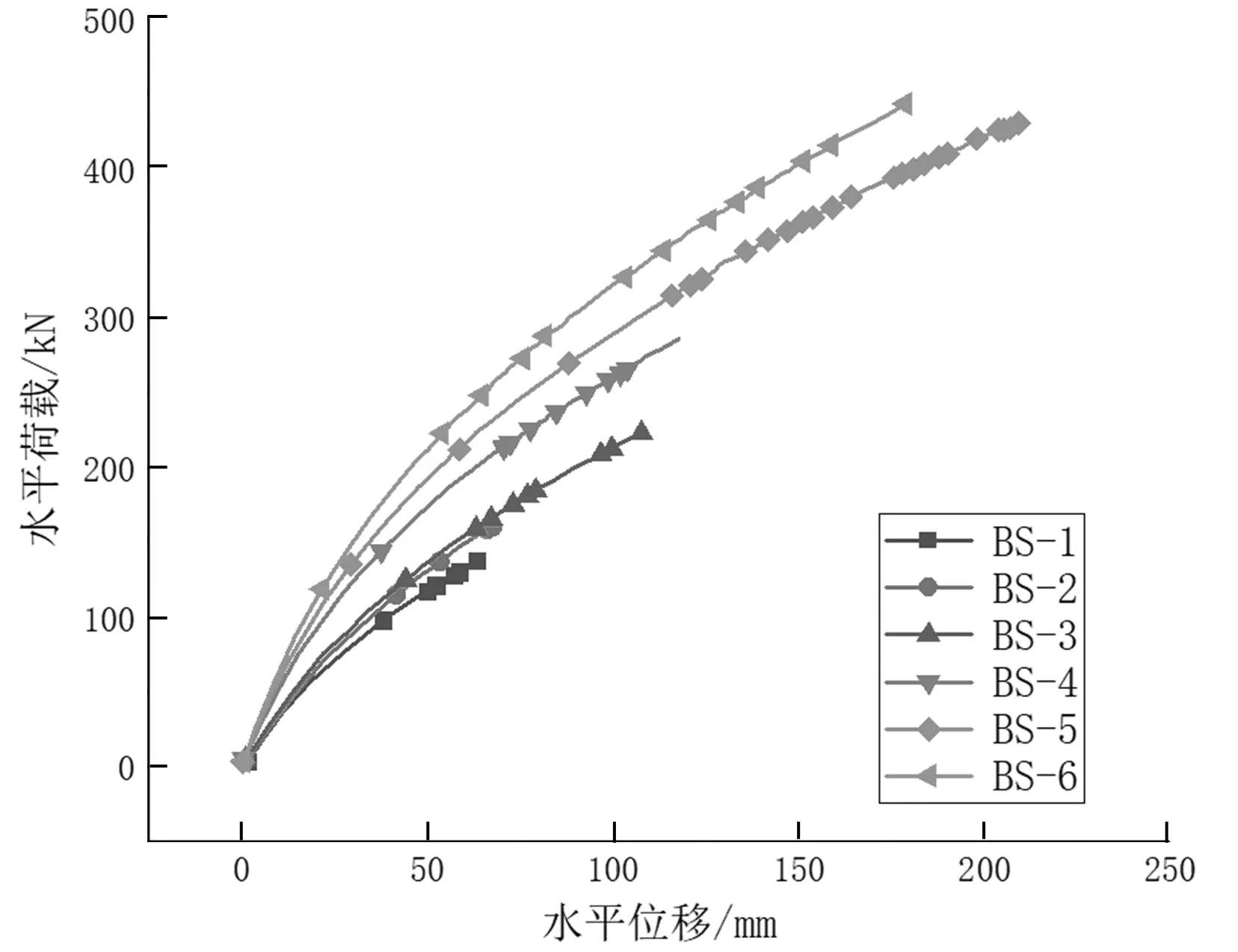
图3 桩身水平荷载-位移曲线

根据图3可知模拟试验桩BS-1、BS-2、BS-3、BS-4、BS-5、BS-6最大的水平承载力分别为138.24 kN、160.45 kN、283.255 kN、286.48 kN、430.6 kN、443.34 kN，具体结果见表3。通过对比分析可知，变截面桩水平承载能力比等截面桩水平承载能力高，且随着变截面位置距离桩顶越远，其水平承载能力越强。

表3 桩身水平承载力对比

2.4.2 桩身位移曲线对比

等截面桩的水平承载力最小，最大水平承载力为138 kN,对6种不同荷载工况的桩施加138 kN的荷载，桩身位移曲线如图4所示。

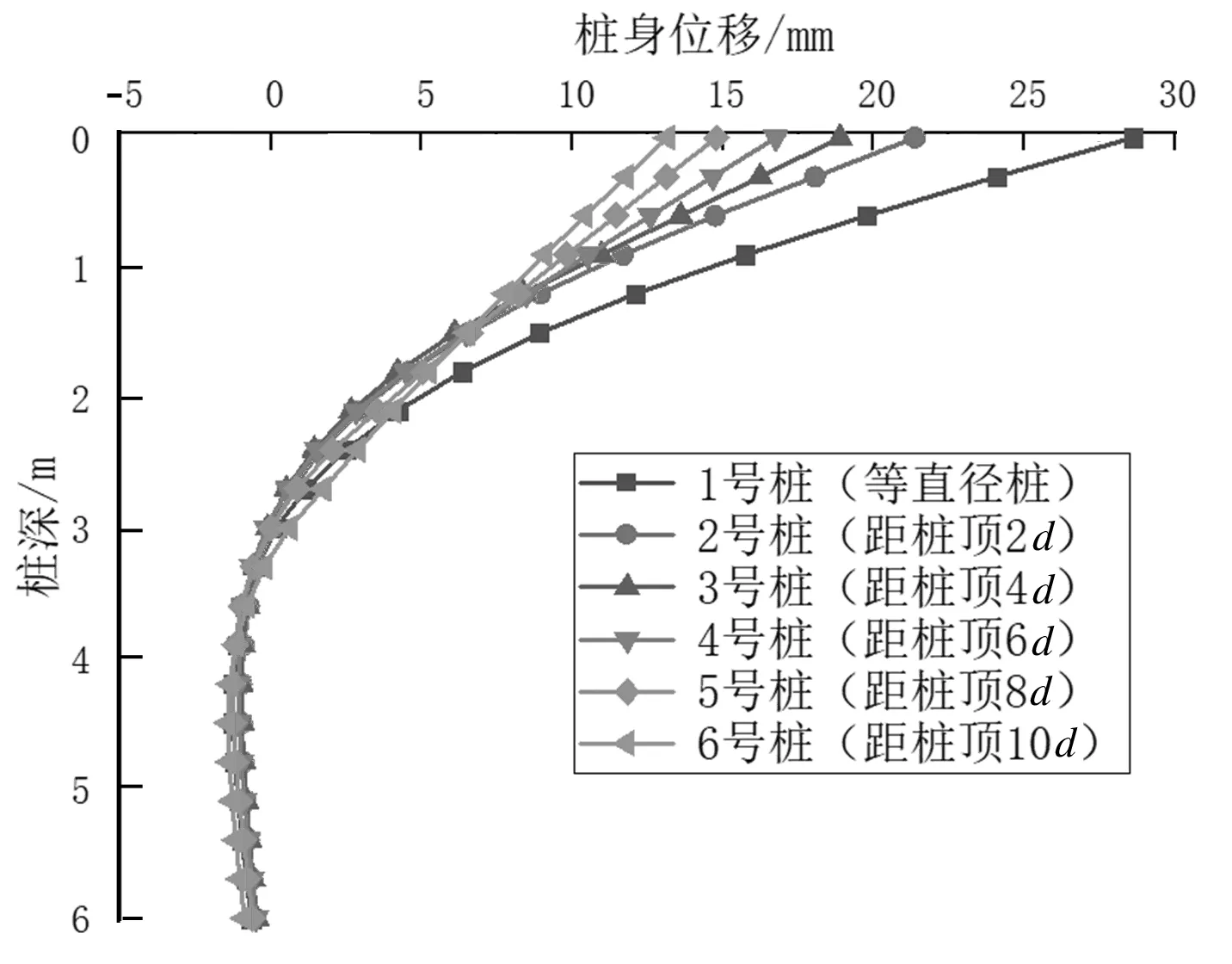
图4 桩身位移曲线

由图4可知，在施加相同的荷载时，等截面桩水平位移最大，最大位移为28 mm，随着变截面位置的加深，桩身刚度逐渐增大，水平位移逐渐减小，桩身水平位移沿着桩身的变化曲线逐渐变缓，说明设置变截面有利于减小桩身水平位移。

2.4.3 弹性极限与塑性极限变化对比

弹性极限与塑性极限随着变截面位置变化曲线如图5所示。

图5 弹性极限、塑性极限变化曲线

2.4.4 等效弹性、等效塑性应变云图对比

不同工况下的等效弹性、等效塑性的应变云图见表4。

表4 等效弹性、等效塑性应变云图

3 结 论

本文用数值模拟的方式针对变截面桩变截面位置的改变对水平承载能力的影响进行分析，并与等截面桩水平承载能力进行对比,得到以下结论：

(1)变截面桩相比等截面桩来说能够有效提升桩身的水平极限承载力，随着变截面位置距离桩顶越来越远，变截面桩的水平承载力得到显著提升，当变截面位于距桩顶10d(即3 m)处时，极限承载力最大为443.34 kN。

(2)对施加相同荷载的等截面桩与变截面桩的桩身位移曲线进行对比分析发现，设置变截面能够减小桩身水平位移，随着变截面位置距离桩顶越来越远，桩身水平位移有明显减少。

(3)弹性应变主要集中于桩身右侧土体，水平荷载作用下，桩身向右侧倾斜，对右侧土体产生挤压作用，最大弹性应变区范围集中在2d至8d的位置处。

(4) 等效塑性应变主要集中于桩土接触的土的上半部分。当变截面处于距离桩顶2d位置处时，变截面以下部分存在一部分土体产生等效塑性应变。随着变截面位置距离桩顶越来越远，等效塑性应变范围逐渐增大。在距离桩顶6d处之后，仅管变截面位置距离桩顶越来越远，但桩侧土体的塑性应变的区域不再有较大的发展。

(5)弹性极限随着变截面位置距离桩顶越来越远是逐渐增加的，塑性极限在变截面位于10d处，其在提高承载力的同时减小了水平位移值。