一种舰载一维相控阵二次雷达高精度算法

左航洲，余 苗，毛梦月，郑 刚

一种舰载一维相控阵二次雷达高精度算法

左航洲，余 苗，毛梦月，郑 刚

（中国电子科技集团公司第二十研究所，西安 710068）

随着现代雷达技术发展，特别是相控阵雷达技术的引入，高精度已成为雷达技术发展的必然趋势。船摇、航向对舰载雷达精度都带来了一定的影响，本文基于舰载一维相控阵二次雷达提出一种高精度算法，以实现舰载二次雷达的精密稳定跟踪，提高跟踪精度。

舰载雷达；一维相控阵；二次雷达；高精度

0 引言

二次雷达[1-2]起源于空管雷达信标系统，采用询问应答协同式工作原理。近年来美军将二次雷达技术引入舰载武器装备系统[3]，作为舰载敌我识别系统[4]的切实应用。国内也将二次雷达技术应用到国防、通信等领域，二次雷达的询问、应答特点相对传统一次雷达具备更高精度，特别是相控阵雷达技术[5]的发展，高精度、高速扫描成为雷达技术发展的趋势。

舰载一维相控阵二次雷达采用协同测量可提供舰船成员之间的舷角和距离，舰船的摇摆对舰载雷达高度所引起的变化，对舰载一维相控阵雷达的测量精度[6-7]带来了一定的影响，本文针对舰载一维相控阵二次雷达，提出一种基于高度坐标转换迭代算法（Altitude based Coordinate Transformation Iterative Algorithm，A-CTI）。

A-CTI算法是基于舰船雷达安装时建立的各成员舰载雷达天线安装高度位置要素表格，采用垂直捷联实时测量各成员雷达天线姿态信息，通过雷达天线互相发射各成员雷达天线的姿态信息，最终可解算出各成员雷达天线的实时高度，采用高度坐标转换迭代算法，有效地提高了舰载一维相控阵二次雷达的舷角测量精度。

1 A-CTI算法实现过程

A-CTI算法实现过程如图1所示。

步骤1：读取安装基线信息

各成员舰载雷达天线安装时建立各成员舰载雷达天线安装基线信息表格，使用时通过成员编号查找安装基线信息表格，读取相应编号成员舰载雷达天线安装基线信息。

步骤2：捷联测量天线姿态信息

垂直捷联和雷达天线安装的舰船同一水平基面，可实时测量雷达天线的姿态信息。

步骤3：雷达天线发射互测成员姿态信息

舰载二次雷达按照时分和频分工作，各成员舰载雷达之间互相跟踪测量，雷达在跟踪测量时，互相交换雷达天线姿态信息给对方，以便解算出互测成员的雷达天线姿态信息。

步骤4：解算互测成员雷达天线高度

读取本舰雷达天线安装基线中高度信息，通过本舰的垂直捷联测量出本舰雷达天线姿态信息，可解算出本舰雷达天线的海拔高度；读取被测编号成员舰载雷达天线安装基线中高度信息，通过雷达天线接收到被测编号成员舰载雷达天线姿态信息，可解算出被测编号成员舰载雷达天线的海拔高度。最终可计算出成员舰载雷达天线的海拔高度差值0。

步骤5：基于高度坐标转换迭代计算。

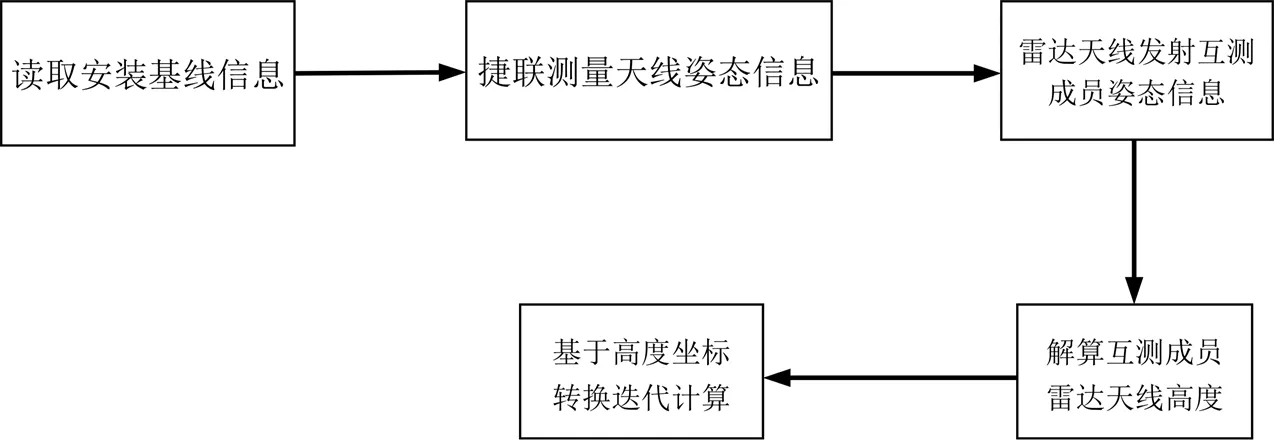
图1 基于高度坐标转换迭代算法流程图

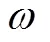
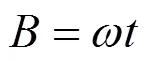
转换到稳定直角坐标如式（2）所示：

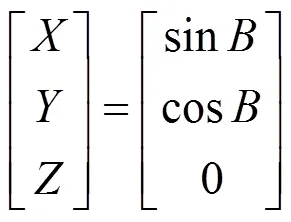
转换稳定甲板直角坐标到不稳定甲板直角坐标如式（3）所示：

式中，舰艇不稳定甲板坐标转换到大地坐标的转换矩阵如式（4）所示：

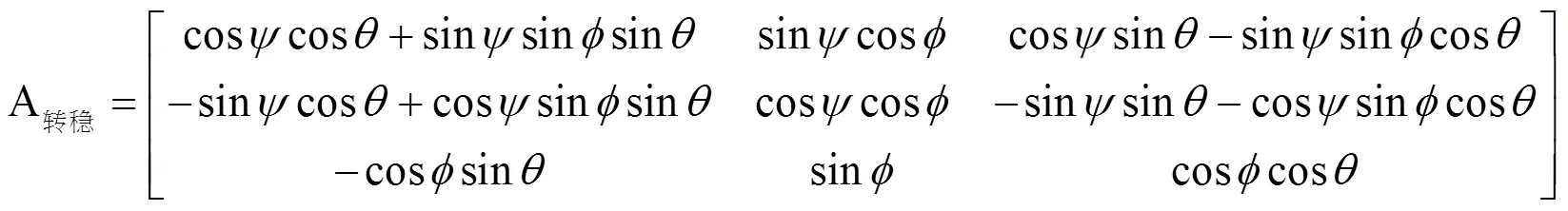
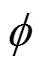
转换到不稳定甲板球坐标，得到相扫角如式（5）所示：

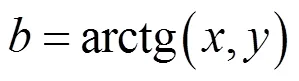
按照布相，即可实现大地等速扫描。

跟踪在不稳定甲板坐标系下进行闭环，跟踪后得到角度，距离，假定俯仰角为（初始设为0）。

转换到不稳定直角坐标系（以下小写表示不稳定坐标，大写表示稳定坐标）如式（6）所示：

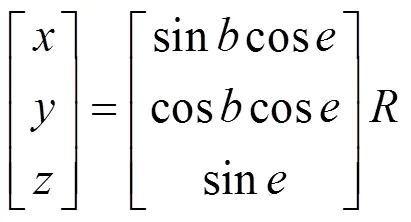
再转换到稳定甲板直角坐标如式（7）所示：

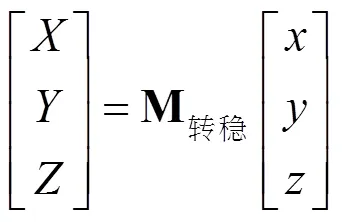
通过A-CTI算法实现过程的步骤1～4可解算出0为互测成员舰载雷达天线高度差值，用0代替式（7）中的后，变回到不稳定甲板坐标系如式（8）所示：

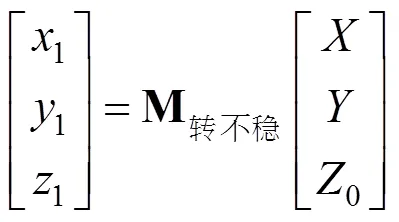
舰艇不稳定甲板坐标转换到舰艇稳定甲板坐标的转换矩阵如式（9）所示：

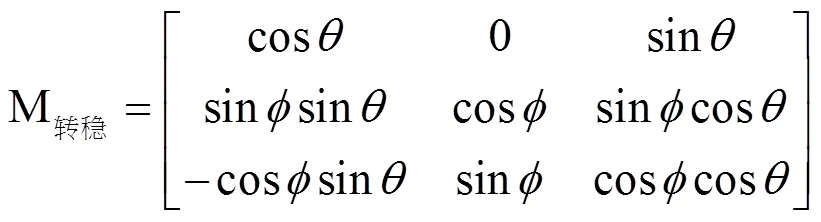
舰艇稳坐标转舰艇不稳定坐标转换矩阵为M的逆阵如式（10）所示：

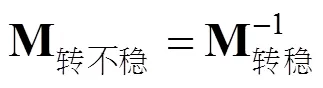
计算如式（11）～式（12）所示：

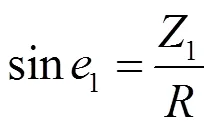
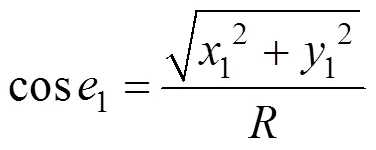
把sin1和cos1代替式（6）中sin和cos进行迭代运算。经仿真，迭代6次，在最大摇摆条件横摇22.5°、纵摇7.5°情况下，计算误差不超过0.0001°，如表1和表2所示。

迭代6次后，再转为稳定甲板球坐标如式（13）所示：

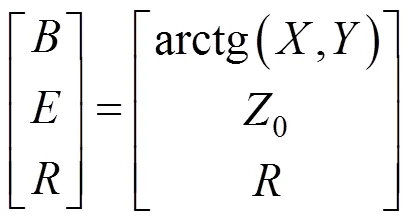
即可得到系统需要的稳定甲板球坐标。式中，0为互测成员舰载雷达天线高度差值，通过A-CTI算法实现过程的步骤1～4可解算出。

2 实验结果及分析

如图2所示，实验架设甲、乙两站，雷达天线为4面阵一维相控阵二次雷达，每个天线阵面相扫±47°，4个阵面覆盖360°全方位扫描。转台模拟航向，摇摆台模拟船摇，捷联输出天线姿态信息。

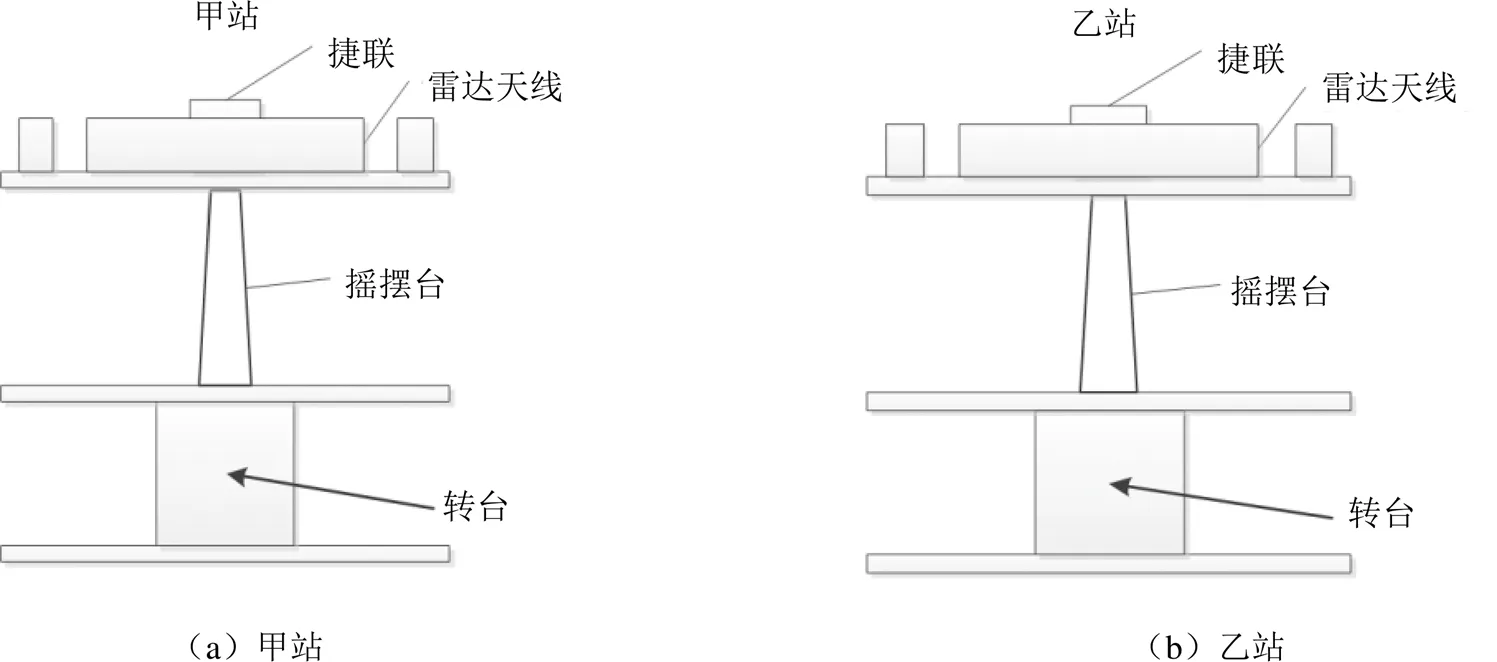
图2 实验雷达天线架设图

2.1 实验结果

用Matlab按照实验模型进行仿真，方位精度单位为度。A-CTI算法迭代1～6次计算可得出实验仿真结果如表1～表2所示。

2.2 结果分析

甲乙两站相距2 km时，目标方位角度越大忽略高度方位精度越差；A-CTI算法迭代数次越多方位精度越高，该算法收敛性好。

表1 甲乙两站相距2 km、天线高度差10 m、目标方位0°时实验结果

表2 甲乙两站相距2 km、天线高度差0 m、目标方位45°时实验结果

3 结论

舰载一维相控阵雷达只能测量方位和距离，不能测量俯仰角度，当舰船摇摆量小时，方位精度是能保障的；当舰船摇摆量很大、目标远离天线法线方向时，方位精度会很差。

A-CTI算法是基于舰载雷达安装时建立的雷达天线安装基线表，采用二次雷达询问、应答原理发射成员舰载雷达天线姿态信息，可对舰载一维相控阵雷达高度进行迭代计算，随着迭代次数越多雷达测量方位精度越高。由此可知，该算法收敛性好。

[1] 王洪，刘昌忠，汪学刚. 二次雷达S模式综述[J]. 电讯技术，2008，48（7）：113-118.

[2] 丁鹭飞，耿富录，陈建春．雷达原理[M]. 西安：电子工业出版社，2010.

[3] 周万幸. 舰载雷达的现状及发展趋势分析[J]. 现代雷达，2007，29（9）：1-4.

[4] 刘显勇，徐向东，魏恭，等. 舰载二次雷达发展与展望概述[J]. 雷达与对抗，2018，38（3）：5-7.

[5] 张光义，赵玉洁．相控阵雷达技术[M]. 北京：电子工业出版社，2004.

[6] 栾铸徵，陈舒敏，吴俭. 舰载一维相控阵雷达波束电子稳定研究[J]. 现代雷达，2013，35（8）：14-18.

[7] 张政超，李文臣. 雷达动态精度试验误差分析[J]. 中国电子科学研究院学报，2012，7（3）：289-293.

High Precision Algorithm for Shipboard One-Dimensional Phased Array Secondary radar

ZUO Hangzhou, YU Miao, MAO Mengyue, ZHENG Gang

With the development of modern radar technique, especially the introduction of phased array radar technique, high precision has become the inevitable trend of radar technique development. Ship rolling and heading have a certain impact on the accuracy of shipboard radar. A high-precision algorithm based on shipboard one-dimensional phased array secondary radar is proposed to realize the precise and stable tracking of shipboard secondary radar and improve the tracking accuracy.

Shipboard Radar; One-Dimensional Phased Array; Secondary Radar; High Precision

TN959.6

A

1674-7976-(2021)-03-213-04

2021-01-29。左航洲（1988.07-），陕西咸阳人，硕士研究生，工程师，主要研究方向为雷达数据处理及显控开发。