基于INS/TOA/BA的EKF TDMA数据链定位算法

曹 硕，秦红磊，丛 丽

基于INS/TOA/BA的EKF TDMA数据链定位算法

曹 硕，秦红磊，丛 丽

（北京航空航天大学电子信息工程学院，北京 100191）

高性能相对导航对于数据链网络联合作战至关重要，特别是在某些情况下数据链网络成员可能无法通过绝对定位获取自己的位置，如强干扰环境或者GNSS可见星比较少的复杂定位环境。本文给出了一种时分多址数据链网络成员基于惯导、高度表和TOA信息的相对定位算法，成员通过基于序贯处理的EKF算法对INS/TOA/BA数据进行实时处理，分别利用二维平面位置滤波器和高度滤波器单独进行相对定位。本文对多成员TDMA数据链网络进行相对导航模拟仿真，对比分析了基于序贯处理的EKF定位方法和一般WLS算法定位结果，分析了对定位精度造成影响的不同因素。仿真证明，基于INS/TOA/BA信息序贯处理的EKF算法可以实现TDMA数据链网络导航观测信息的实时处理并提供较为理想的定位精度。

数据链；TDMA ；EKF

0 引言

在大规模联合作战环境中，通过测距确定与其他网络成员的相对位置，在一个共同的相对坐标系下形成统一的敌我态势，相对定位信息的获取对实现任务目标至关重要。作战环境中以卫星导航为代表的绝对定位方式容易受到干扰导致无法正常定位[1-2]。数据链系统发射功率大、信号具有跳频跳时等功能、抗干扰能力强、网络成员之间能够实现时钟同步并进行TOA测距和定位，是GNSS不可用环境下的理想替代定位系统[3]。

数据链网络成员运动状态复杂，成员位置分布比较随机，数据链网络最大作用范围为500 km，但是数据链网络成员中飞行高度较高的飞行成员一般飞行最大高度远小于这个值。数据链网络成员高度方向的高度差远小于二维平面的分布范围，这导致数据链网络高度方向定位几何不好。目前的数据链定位算法如文献[4-6]给出的数据链导航算法，基于成员运动模型建立卡尔曼滤波状态转移矩阵，利用用户收到的成员精确位置与识别（Precise Participant Location and Identification，PPLI）进行TOA信息提取，计算信息之后对滤波器进行校正。为了增加定位的稳定性，很多研究人员选择将数据链提供的TOA观测量和INS进行组合。文献[7-8]中的研究人员将INS信息和数据链提供的TOA信息进行组合，但是针对数据链网络高度方向几何不好的问题没有给出很好的解决方案。针对高度方向定位几何差的问题，很多研究人员选择在高度方向上添加高度传感器的方法来提升高度方向的定位精度。文献[9]提出的方法在可见星不够的情况下加入高度表观测值成功实现GNSS缺星环境下定位。文献[10]利用高度表的观测量解决了高度运动过程中GNSS差分定位高度几何不稳定的问题。文献[11-12]中的研究人员在GNSS定位条件较差的环境下，利用添加高度表观测量的方式成功提升了定位精度。

本文提出了一种基于INS/TOA/BA信息的EKF定位算法，算法利用INS/TOA组合平面滤波器对经、纬度进行定位，利用INS/BA组合高度滤波器进行高向单独定位，可以实现时分多址（Time Division Multiple Access，TDMA）体制下对观测量的实时处理，解决了高度方向定位几何不好的问题并提升了定位进度。

1 数据链相对导航基本原理

相对导航系统由不同的网络角色组成，其网络结构如图1所示。数据链网络角色可以被划分为：

（1）数据链网络导航控制者（Navigation Controller，NC），相对导航坐标系是以NC为原点建立；

（2）数据链系统时间基准（Time Reference，TR），所有成员需通过校时或者无源校时与之同步；

（3）网络位置基准成员（Positioning Reference，PR），网络位置基准成员需要已知准确的绝对位置和相对位置；

（4）一级成员（Primary User，PU），一级成员可以进行有源校时；

（5）二级成员（Secondary User，SU），二级成员只能进行无源校时。

在Link-16数据链系统中，时间系统被划分为了多个层级，将一天24小时等分为112.5个时元，时元长度为12.8 min；每个时元等分为64个时帧，时帧长度为12 s；每个时帧等分为1536个时隙，每个时隙时长为7. 8125 ms。

图1 相对导航定位网络结构

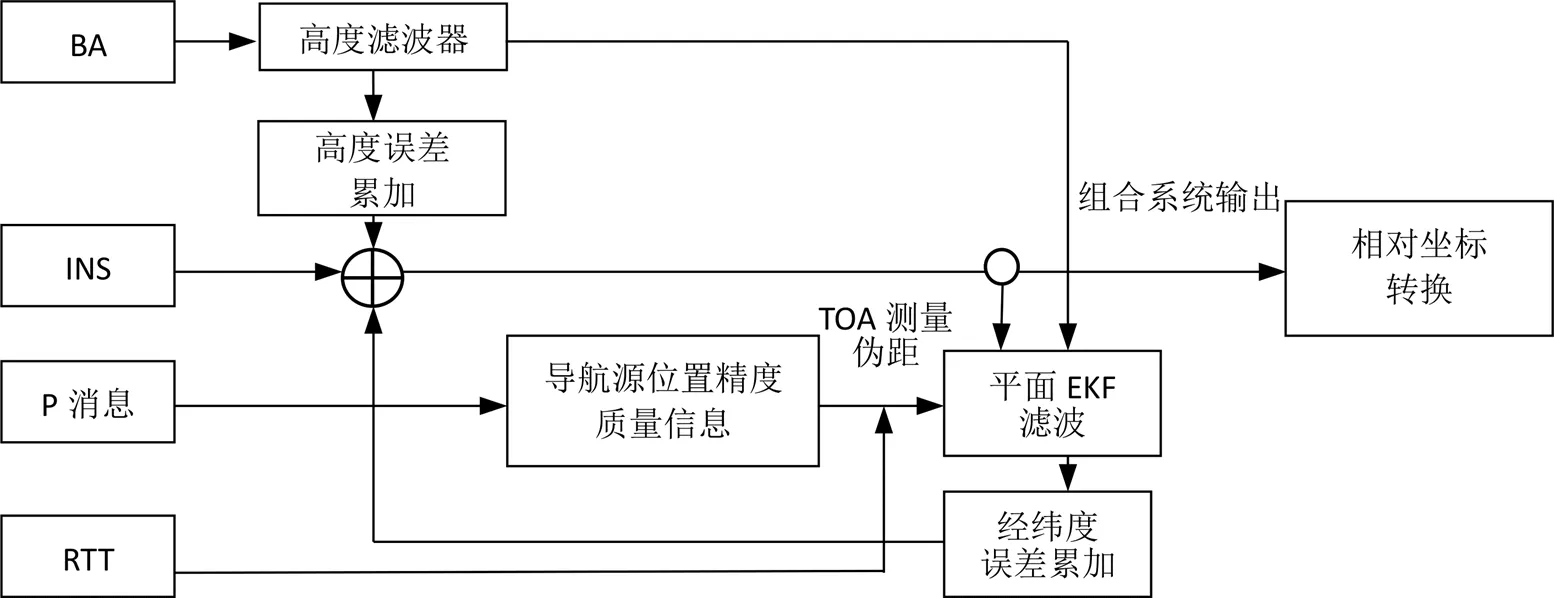
图2 基于INS/TOA/BA的数据链网络相对导航定位算法结构

2 数据链系统定位滤波器结构

数据链成员分布范围较大可达上百公里，但是高度方向高度差相对成员之间距离小很多，这一特点导致高度方向定位几何较差。因此我们利用高度表的观测量进行高度单独滤波，在二维平面上利用TOA观测量进行二维平面滤波。利用往返时延（Round-Trip Time，RTT）滤波器进行时钟误差滤波。基于INS/TOA/BA的数据链网络相对导航定位算法结构如图2所示。

2.1 高度滤波

高度滤波器的观测量为高度表和INS高向输出之间的差量，如式（3）所示：

2.2 RTT滤波器

将频差模拟为一阶马尔科夫过程，状态量为定位用户成员的钟差和频差，状态方程如式（4）所示：

有源校时RTT滤波器的观测方程如式（6）所示：

式中，为RTT测量噪声。

2.3 基于序贯处理EKF的二维平面滤波器

2.3.1状态量及状态方程

假设当前导航时隙为，如式（7）所示预测状态量为7维，分别为平台偏移误差角在东向、北向、高向上的误差角，经、纬度误差和东向、北向速度误差。

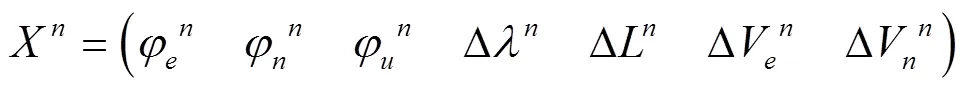
二维平面的滤波器状态方程每个导航时隙都会进行滤波器预测值的更新，二维平面滤波器的离散状态方程如式（8）所示：

2.3.2观测量及观测方程

第个时隙的TOA观测值如式（9）所示：

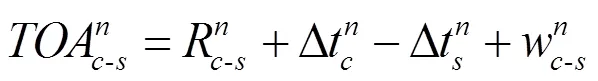
由此得出用户的计算距离如式（10）所示：

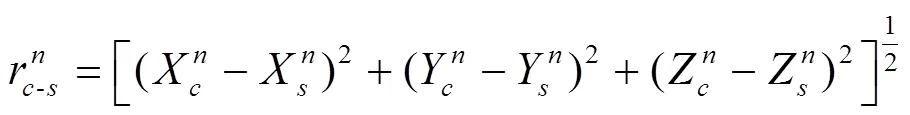
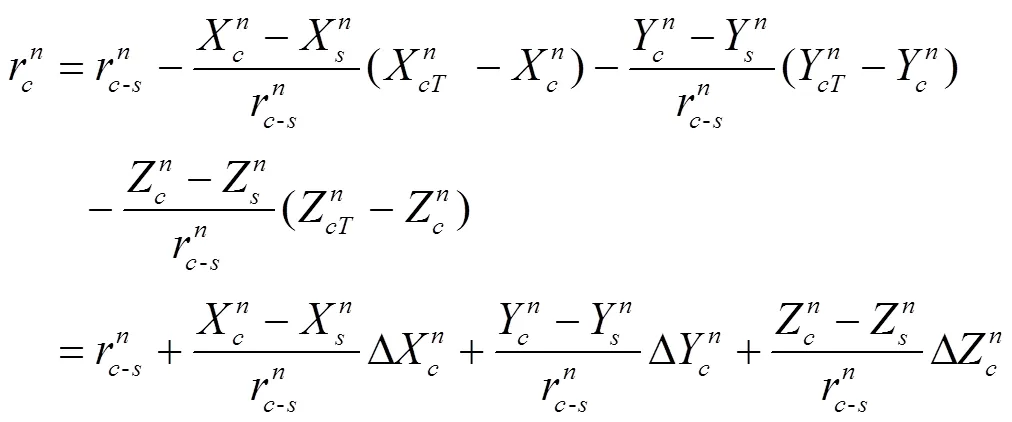
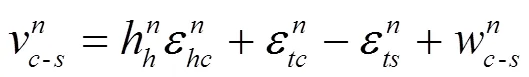
3 仿真实验与分析

利用软件仿真建立数据链仿真网络并进行相对导航定位算法性能测试。仿真系统在提前配置好的真实轨迹上加上惯导位置、速度和姿态误差来模拟网络成员的惯导输出。TOA观测量是仿真系统在真实距离的基础上加用户钟差和导航源钟差以及测距误差得到，默认测距误差为零均值的高斯白噪声。

3.1 仿真环境

建立一个有8个一级成员的数据链网络，成员角色为飞机，二维平面上的飞行轨迹如图3所示。1号成员为NC，同时将NC作为网络时间基准，1～5号成员为位置基准成员，6～8号成员通过本文所提出的EKF序贯处理方法定位。

成员时钟频率随机误差为3×10-6/ h，TOA测量误差标准差为3 m（1），陀螺仪偏执误差为0.1°/ h，加速度计误差为0.0001g（1）。每帧共192个导航时隙，成员12 s一次RTT。

本文会在几种情况下观察成员8的定位结果并做出分析，8号成员起始地理位置经纬度坐标为（113.7°，37.4°），高度为5500 m。

3.2 定位算法仿真对比

将EKF序贯处理定位算法和一般最小二乘算法进行对比。一般最小二乘无法对成员接收到的TOA观测量按照时隙进行实时处理，高向也会利用相同的高度滤波器定位，定位误差曲线如图4所示。

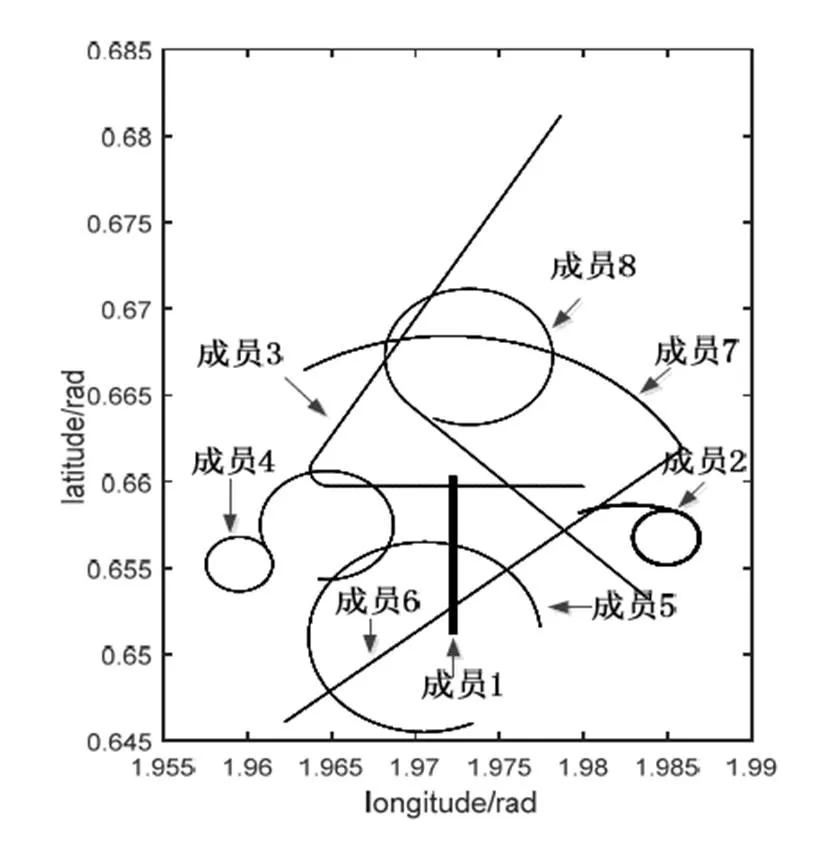
图3 成员二维轨迹分布图

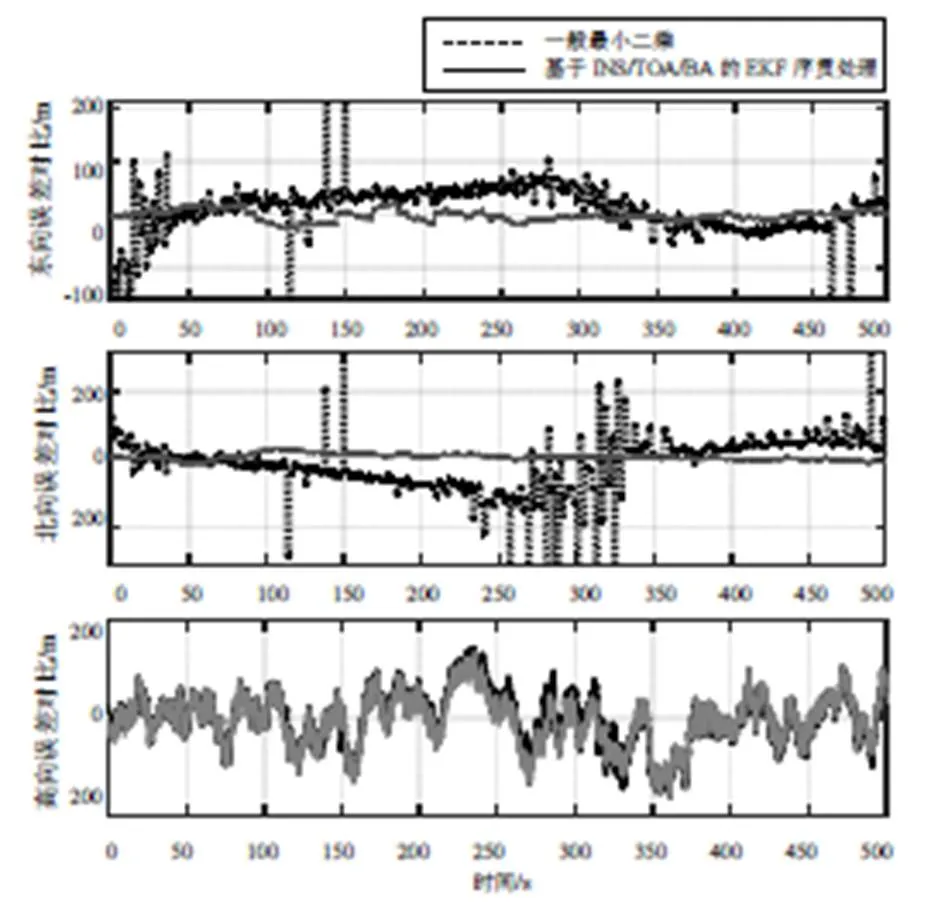
图4 实时误差对比结果

对比统计结果均方根误差（Root Mean Square Error，RMSE）如图5所示，基于序贯处理的EKF序惯处理方法可以比较好地应对TDMA数据链成员在不同的时隙和位置接收到导航源的信息无法在同一时刻进行解算的问题，而一般最小二乘在TDMA体制下无法很好地进行定位解算，定位效果一般。

3.3 算法性能影响因素分析

3.3.1 TOA测量精度误差影响分析

在不同TOA测量误差条件下分析TOA测距误差并提出算法定位精度的影响，分析结果如图6所示。在解算过程中将TOA的时间观测量值转为以米为单位的量值，因此对比中所设置的TOA误差值也相应设置成以米为单位的1σ误差。

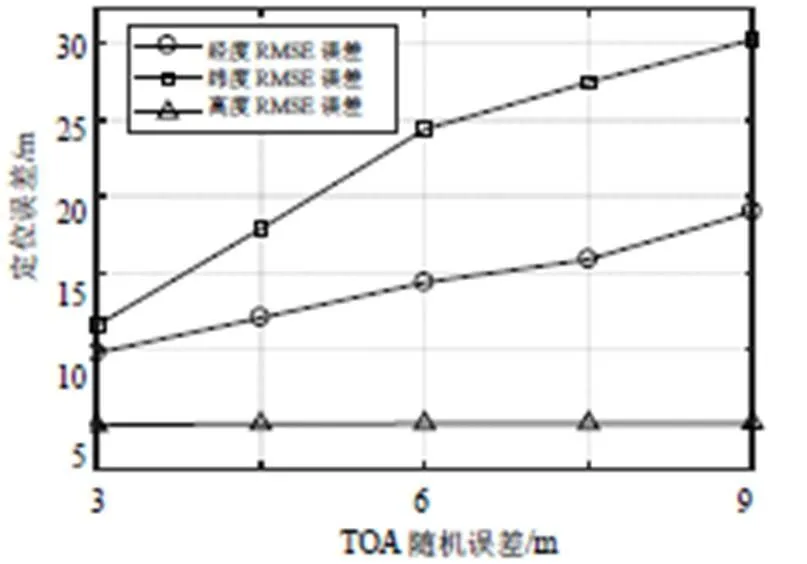
图6 TOA测距误差影响分析

成员二维定位精度和TOA测距误差之间正相关，但是高向定位观测量为高度表，因此不受TOA精度的影响。

3.3.2 PPLI消息时隙播发频率影响分析

数据链基础时隙设置为7.8125 ms，分别将PPLI播发时隙间隔设置为8、16、24、32、40个基础时隙一次，以8号成员为观察者，定位结果如图7所示。

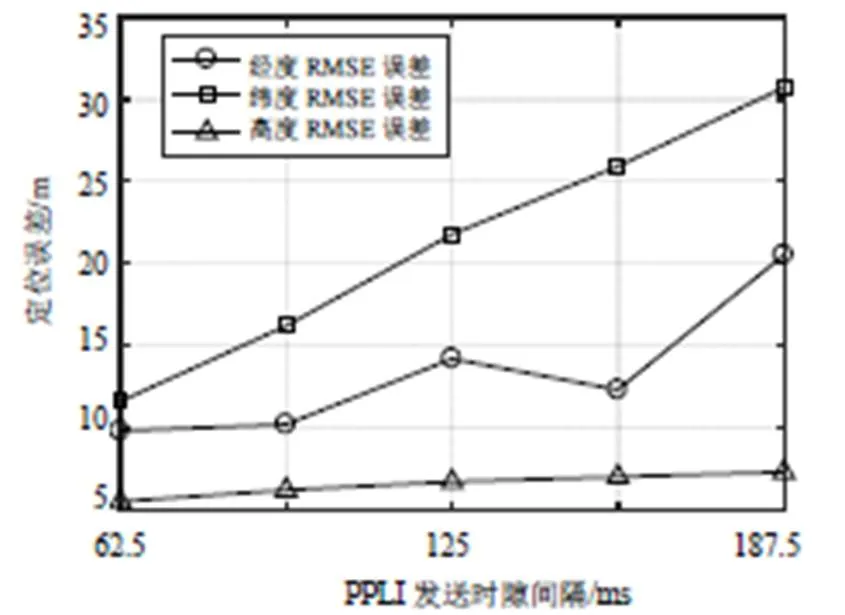
图7 滤波时隙间隔影响分析

每发送一次PPLI消息定位用户会提取TOA观测量进行一次滤波，从分析中得到：滤波间隔越大，单位时间内可用TOA观测量越少，滤波器系统噪声越大，定位精度降低。

4 结论

基于INS/TOA/BA的序贯处理EKF数据链网络相对导航定位算法，解决了TMDA网络定位成员在不同的时间和位置收到同导航源的信息进行定位无法实时解算的问题。本文通过软件仿真建立数据链网络，将提出的算法和一般最小二乘算法进行对比，并进行算法精度影响因素分析。仿真结果表明，在数据链TDMA体制下，序贯处理EKF数据链网络相对导航定位算法在二维平面有良好的定位效果。本文提出的数据链网络相对定位算法为TDMA体制的数据链定位提供了理论基础。

[1] Felter S C , Wu N E . A relative Navigation System for Formation Flight [J]. IEEE Trans. Aerosp. Electron. Syst., 1997，33（3）：958-967.

[2] Aghadadashfam M, Mosavi MR, Rezaei M J. A New Post-correlation Anti-jamming Technique for GPS Receivers. GPS Solut. 2020，24：89.

[3] Da G X, Nan W, Wang C, et al. Anti-jamming Performance Simulation of Tactical Data Link Communication System[C]// Antennas, Propagation & EM Theory (ISAPE)，2012 10th International Symposium on. IEEE，2012.

[4] Qiang L, Jingming K, Zhiming B, et al. Joint Analysis and Simulation of Time Synchronization Relative NavigationPerformance of a Kind of Wireless TDMA network[C]// International Frequency Control Symposium & Exposition，2007.

[5] Fried W R. Principles and Simulation of JTIDS Relative Navigation [J]. IEEE Transactions on Aerospace & Electronics Systems，1978，AES-14（1）：76-84.

[6] Altrichter W W . JTIDS Relative Navigation and Data Registration[C]// IEEE Position Location & Navigation Symposium，1992.

[7] Felter SC, Wu N E. A Relative Navigation System for Formation Flight. IEEE Trans. Aerosp. Electron. 1997，33： 958–967.

[8] Liu W, Wu S, Wu X. Relative Cavigation of Missile Formation and INS Error Correction Methods[C]// Control & Decision Conference，2017.

[9] Kirkko Jaakkola M, Parviainen J, Collin J. Improving TTFF by Two-Satellite GNSS Positioning[J]. Aerospace & Electronics Systems IEEE Transactions on 2012，48（4）：3660-3670.

[10] Lee D S, Park K W, Park C, et al. An Efficient Heave Estimation Using Time-Differenced GPS Carrier Phase Measurements and Compensated Barometer Measurement Applying Error Model[C]//2015 International Association of Institutes of Navigation World Congress，2015：1-6.

[11] Chiang K W，Chang H W，Li YH，et al. Assessment for INS/GNSS/Odometer/barometer Integration in Loosely-coupled and Tightly-coupled Scheme in a GNSS-degraded Environment [J]. IEEE Sens. J. 2020，20：224-236.

[12] Matteo A, Marica B, Carlo B, et al. Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys [J]. Sensors，2017，17（8）：1889.

Datalink Positioning Algorithm of EKF TDMA Based on INS/TOA/BA

CAO Shuo, QIN Honglei, CONG Li

Relative position is very important tactical information in large-scale joint military operations,especially in some cases that the members of the datalink network may not be able to obtain their position through absolute positioning, such as the environment with strong interference or environment with fewer visible GNSS satellites. The EKF (Extended Kalman Filter) algorithm based on INS/TOA/BA is proposed in the paper, members of network can process INS/TOA/BA data in two-dimensional plane timely, and height is positioned with height filter.A simulation of TDMA relative navigation network is carried out to verify the performance of proposed algorithm. The results show that compared with general WLS (Weighted Least Squares) the proposed algorithm can realize the real-time processing of TOA information in TDMA datalink network and achieve a satisfactory accuracy.

Datalink; TDMA; EKF（Extended Kalman Filter）

TN919

A

1674-7976-(2021)-03-157-06

2021-04-12。曹硕（1986.11-），河北承德人，博士，主要研究方向为数据链相对导航。