纤维缠绕Kagome网格卫星承力筒承载性能分析及结构优化研究*

孙守政，孙天峰，陈维强，范东兴，韩振宇，富宏亚

（1.哈尔滨工业大学，哈尔滨 150001；2.中国空间技术研究院北京卫星制造厂有限公司，北京 100094）

碳纤维增强型复合材料具有轻质、高强、耐腐蚀、极端环境适应性好、可设计性强等特点，被广泛应用于航空航天、能源开采、建筑、交通等多个领域中[1–2]。在航空航天领域，复合材料可以替代传统铝合金、钛合金等金属构件，既减轻了质量，又提升了构件的可靠性。国外将复合材料使用率作为评价飞机先进程度的重要指标。例如，在波音787客机机翼及机身上所使用的复合材料比重可达50%，而上代波音777客机仅使用了12%的复合材料，由此可见，复合材料已经成为航空航天领域无法替代的应用材料，在国家“大飞机”、“载人航天与探月工程”、“天问一号”、“北斗卫星导航”等重大工程中的作用越来越突出[3–4]。承力筒是卫星中的重要承力部件，对卫星总体力学性能及服役性能至关重要。卫星承力筒的设计与结构优化是进一步减轻重量、提升承力结构及承载性能的重要前提[5]。航空航天结构件设计中，有两种基本的复合材料结构设计思想：一是基于承载蒙皮纵梁加强结构和蜂窝夹层结构；二是无蒙皮的网格加强结构。相较于承载效率而言，无蒙皮的网格结构所受载荷完全由相互交错的加强筋承受，因而其承载效率高于有蒙皮的纵梁加强结构和蜂窝夹层结构。早期的网格加强结构通过机械加工铝合金的方式得到，但采用纤维增强复合材料成型的网格结构能实现减重20%以上，同时，网格加强筋交错的节点处可以增强整体结构的阻尼特性，具有良好的抗冲击性能[6–7]。

网格加强结构的成型方式有多种，包括缠绕、铺放、编织、互锁工艺、真空辅助树脂传递模塑等十余种。其中，具有规则回转体形状的网格构件，其缠绕成型有明显的优势：技术成熟、自动化程度高、效率高、纤维连续等。网格构件大多采用干法缠绕，其原理是将纤维预浸丝/带，按照网格轨迹缠绕到网格芯模上，并增至规定的厚度，随后进行固化脱模，形成网格加强结构。然而网格构件结构尺寸较多，且参数之间相互耦合，同时结构参数对网格结构整体力学性能的影响尚未明确，限制了其在航空航天领域上的应用，因此，对网格构件进行结构设计优化，以确定适宜的结构参数，是满足网格结构强度及可靠性的重要前期保障[8]。

现阶段，国内外学者对网格缠绕构件已经开展了一定的基础性研究工作。Belardi等[9]对受到不同外载的圆柱形网格构件进行了结构分析及参数优化，采用有限元法，计算网格结构的临界屈曲荷载，探究了屈曲破坏模式，最后基于遗传算法对结构进行了参数优化，减少了结构的整体质量。Yazdani等[10]研究了在准静态轴向载荷作用下的薄壁圆柱壳网格加强结构的屈曲行为，结果表明，较少的加强筋数量能够提升结构强度。此外，在轴向载荷作用下，螺旋肋比环肋对屈曲性能的影响更为显著。南京航空航天大学的Li等[11]为主网格加强筋和次网格加强筋加强结构设计，其中主加强筋更厚，有助于提升网格构件的整体抗弯刚度，而次加强筋则可以提升局部的抗弯刚度。哈尔滨工业大学的张鹏[12]提出利用螺旋肋和环向肋的数量表征网格密度，制定了新型网格缠绕成型工艺，提出多丝嘴缠绕方案，即螺旋肋与环肋同时缠绕，以减少网格交叉点架空与堆积等节点缺陷，并建立了多丝嘴网格缠绕的数学模型。

虽然网格结构缠绕技术已取得一定成果，但网格结构具有较强的可设计性，如何通过优化结构提升承载效率，尚未有充分的参数化理论模型。此外，网格结构参数较多，参数之间相互耦合，采用试验试凑法优化结构成本较高、效率较低。为此，本文针对以上问题，以卫星Kagome网格承力筒为研究对象，开展结构优化研究。采用有限元方法，得到现有工况条件下网格承力筒的承载性能。通过参数化建模及加强筋独立设计的思路，获得各个结构参数对承载性能的影响；采用多目标遗传算法，优化了结构参数，并对最优结构的强度、屈曲性能进行分析；最后，采用自主研制的桌面式缠绕机对网格承力筒进行了缠绕成型。

网格承力筒有限元模型及其边界条件

1 网格承力筒有限元模型

网格承力筒主要由螺旋筋及环向筋两个加强筋组成，由于加强筋结构长度方向上尺度远大于截面方向，因此，可以采用三维梁结构等效加强筋结构。本文利用Ansys软件，通过梁单元BEAM189划分承力筒的有限元模型，并对网格承力筒的整体承载性能进行分析及评价。

网格承力筒所用预浸料为M40J环氧树脂预浸料，该预浸料的材料基本属性包括：纤维向杨氏模量Ex=220GPa、垂直纤维向杨氏模量Ey=Ez=7GPa、泊松比νxy=νxz=0.32、νyz= 0.3、剪切模量Gxy=Gxz=6.8GPa、Gyz=6.7GPa、材料密度为1.7g/cm3。网格承力筒的初始几何参数如表1所示。

表1 网格承力筒的初始几何参数Table 1 Initial geometric parameters of grid cylinder

有限元建模时将两条旋向相反的螺旋筋定义为一对螺旋筋，螺旋起点相交定义为初始状态。螺旋筋绕承力筒轴线方向的旋转角度定义为螺旋筋的旋转角。该角度不仅能够确定螺旋筋的位置，还能确定螺旋筋与环筋相交节点的相对位置。根据上述承力筒几何尺寸及网格划分定义的有限元模型如图1（a）所示。根据实际工况条件定义网格承力筒结构有限元模型的边界及承载条件，承力筒底部采用固支约束，并约束前端面的径向位移。根据卫星承力筒的实际工况条件，在前端面利用均布形式施加压缩载荷和水平剪切载荷，如图1 （b）所示。Fx为水平剪切载荷；Fy为轴向压缩载荷。由于前端面环筋各位置的弯矩大小不同，因而各网格具有不同的轴向位移。在螺旋筋和环筋交叉节点附近弯矩最小，环筋变形也较小，但螺旋筋交叉的节点位移较大，这不符合实际轴向压缩试验的变形情况。为了保证模型的准确性，边界条件施加时耦合了前端面单元的轴向位移，使前端面环筋在压缩过程中保持相同的轴向位移。

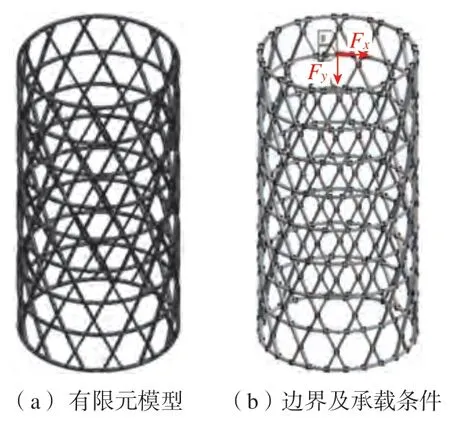
图1 网格承力筒有限元模型及边界条件的施加Fig.1 Finite element model and boundary conditions of the grid cylinder

2 承载性能分析

根据网格承力筒的有限元模型及边界条件，分析水平剪切载荷Fx在300kN、轴向压缩载荷Fy在60kN的受力下整体变形及应变情况，如图2所示。

由图2（a）可知，该工况下承力筒发生轴向位移及水平位移，最大变形量为2.89mm。由图2（b）可知，由于螺旋筋主要承受轴向压缩载荷的作用，环筋主要承受水平剪切载荷的作用，因此，螺旋筋内部以压应力为主，环筋以拉应力为主。由于受到该工况载荷的共同作用，导致上半侧左螺旋筋的压应力大于右螺旋筋，下半侧则相反。应力最大值在下半侧右螺旋筋处，为735.26MPa。对于环筋的拉应力的规律基本与螺旋筋一致，即上半侧左环筋拉应力比右环筋大，下半侧反之，最大值在上半侧第2环筋左侧，为302.01MPa。由图2（c）可知，切应力在承力筒左上部及右下部较大，其中最大值在右下部的螺旋筋及下端面环筋交叉节点处，为367.63MPa。综上所述，虽然压缩载荷比水平剪切载荷小，但筋条的压应力明显高于其他方向应力，说明该种工况下，筋条应力以压应力为主。

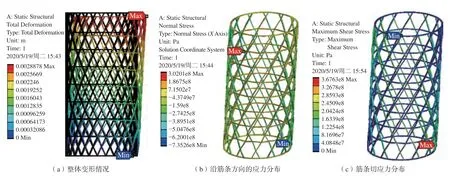
图2 网格承力筒在特定工况下的变形及应力场分布Fig.2 Deformation and stress distribution of grid cylinder under specific working condition

网格承力筒结构参数对承载性能的影响

1 网格承力筒参数化几何模型

本部分采用Ansys参数化建模方法，网格承力筒构件的有限元模型，其中重要的参数包括：承力筒直径D、承力筒高度H、承力筒螺旋角A、同向螺旋筋数量M、螺旋筋旋转角度P、环向筋距离（H2～H8）、加强筋厚度T与宽度W，网格承力筒几何模型如图3所示。

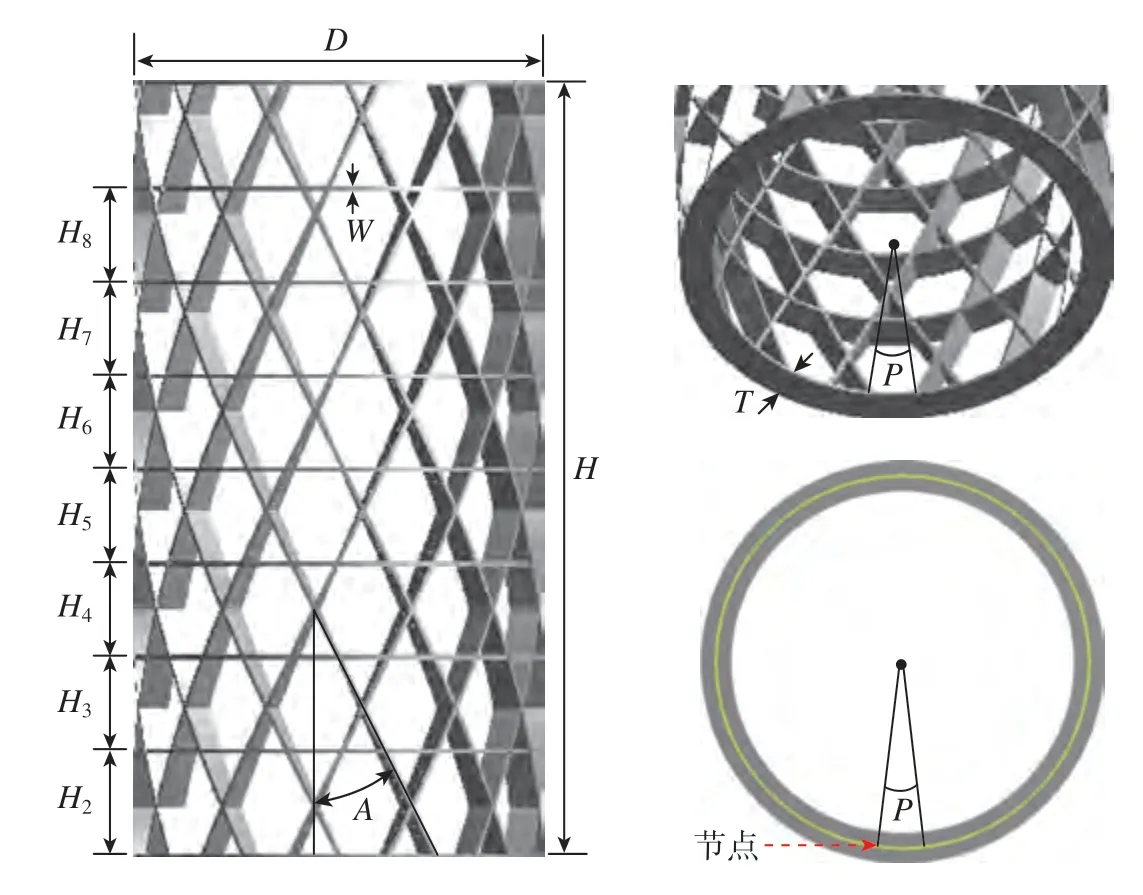
图3 网格承力筒几何模型Fig.3 Geometric model and parameters of the grid cylinder

为了减少螺旋筋与环筋结构参数之间的耦合作用，本部分提出结构的并行设计概念，将螺旋筋和环筋的结构设计相对独立，从而避免两种结构设计的相互干涉和不符合使用工况的情形。由前文分析可知，筋条应力以压应力为主，在此工况下，承力筒最可能首先发生的是压缩失效。因此，本部分以筋条最大压应变与整体质量的比值来表征承力筒的承载效率，用承载效率系数Q表示。单位质量的应变越小，Q值越小，承载效率越高。网格承力筒的质量m可由式（1）得出：

其中，ρ为网格承力筒密度；n为环筋数量。

2 螺旋角对结构承载性能的影响

参照表1，保持其他几何参数不变，螺旋角设置范围为[0°，60°]。从承力筒的质量来讲，螺旋角为0°时，质量最小，原因是所用螺旋筋长度最短，螺旋角为60°时质量最大。根据式（1）计算，螺旋角在约束范围内，承力筒质量在18kg至30kg之间。螺旋角A对最大压应变、拉应变、剪切应变、质量承载效率系数Q的影响规律，如图4所示。

由图4可知，螺旋角对各承载性能参数的影响规律基本一致，均随着螺旋角的增加呈现先极速下降后缓慢上升的趋势。螺旋角在15°～20°时，筋条最大压应变、筋条拉应变、剪切应变值最小，且承载效率系数最低，说明螺旋角在此区间内，承力筒承载效率最高。此外，螺旋角在0°～10°时，承载效率降低速率最快，此时剪切应变占主导地位，较小的螺旋角承载剪切载荷能力较弱，且无螺旋角时完全无法承受剪切载荷，因此，承载能力下降较快。而虽然较大的螺旋角承载压缩载荷的能力弱，但设定的最大螺旋角为60°，一定程度上也能承受一些压缩载荷，因此，曲线后期会缓慢上升。综上所述，网格结构承载能力与螺旋角关系密切，可见螺旋角是网格结构的重要设计参数之一。

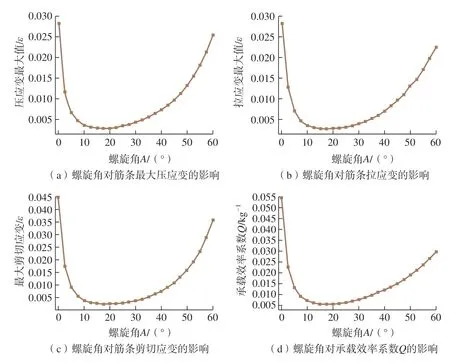
图4 螺旋角对结构承载性能的影响Fig.4 Effect of helix angle on load-bearing performance

3 螺旋筋旋转角对结构承载性能的影响

保持其他几何参数不变，详见表1，探究螺旋筋旋转角P对结构承载性能的影响规律。由图1可知，螺旋筋旋转角不同，环筋和螺旋筋之间的交叉节点位置会发生改变，从而影响结构整体力学性能。设定螺旋筋旋转角P取值范围为[0°，60°]，设计点为60个。由于螺旋筋旋转角P对结构质量的影响不大，因此，螺旋筋旋转角P与承载效率关联性较小。本部分主要探究螺旋筋旋转角P对承力筒筋条最大压应变、轴向位移及轴向刚度的影响，如图5所示。

由于同向螺旋筋数量为13，因而螺旋筋旋转角每过27.69°为一个周期，螺旋筋旋转角在0°～60°范围内应循环约2.2个周期。由图5所示，周期性变化与计算基本一致，从压应变变化趋势中发现，在单个周期中呈现上升–下降–再上升–再下降的变化特征。其原因是当螺旋筋旋转角较小时，不同旋向的螺旋筋下端部距离较近，最大压应变发生在下端部螺旋筋与环筋的交叉节点处，随着螺旋筋旋转角增加，最大压应变值降低，直到螺旋筋旋转角增加到5°左右时，不同旋向的螺旋筋上端部距离较近，此时最大压应变的位置发生变化，在上端部螺旋筋与环筋的交叉节点处，随着螺旋筋旋转角继续增加，最大压应变值降低。螺旋筋旋转角对轴向位移及轴向刚度的影响规律基本一致，呈现先上升后降低的趋势，其中螺旋筋旋转角在约23°时，轴向位移出现最小值约1.185mm，轴向刚度出现最大值约2.535×105N/m。

图5 螺旋筋旋转角对结构承载性能的影响Fig.5 Effect of rotation angle on load-bearing performance

4 筋条形状对结构承载性能的影响

本部分主要探究筋条宽度及厚度等形状特征对结构承载性能的影响。在其他结构参数不变的情况下，分别设定筋条宽度及厚度的变化范围为[2mm，20mm]，均匀选取范围内的10个设计点。由式（1）计算出不同筋条形状参数对承力筒质量的影响，发现筋条宽度及厚度对承力筒质量均呈现线性正相关关系，而筋条最大压应变呈负相关关系，如图6所示，可知筋条宽度及厚度的增加可以提升轴向刚度。

图6 筋条形状对结构承载性能的影响Fig.6 Effect of rib shape on load-bearing performance

从图6可以看出，随着筋条厚度的增加，结构最大压应变下降速率较快，由此得知，筋条厚度对承载性能的影响会更大。通过对结构件的轴向刚度分析发现，筋条宽度和厚度均与轴向刚度呈线性正相关关系，但筋条厚度对轴向刚度的关系斜率明显大于筋条宽度，因此说明筋条厚度对轴向刚度的影响也较宽度显著。

网格承力筒结构参数优化及工艺实现

1 基于多目标遗传算法的结构参数优化

基于以上仿真分析及几何参数与承载性能的关系分析，对网格承力筒进行结构参数优化。由于多目标遗传算法（Multi-objective genetic algorithm, MOGA）具有响应速度快、不需要训练、可以处理离散变量等优势，适合网格承力筒结构参数优化的计算。网格承力筒结构参数优化流程包括：设计变量选择、约束条件确定、目标函数的确定、优化计算及结果分析等。设计变量包括螺旋角A、螺旋筋旋转角P、环筋间距（H2～H8）、筋条宽度W及筋条厚度T。约束条件的确定可依据几何参数与承载性能的关系，如表2所示。

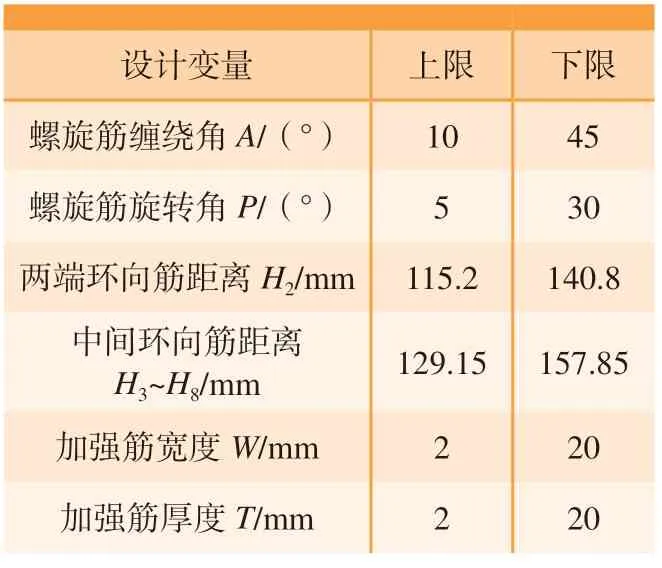
表2 网格承力筒几何参数的约束条件Table 2 Constraint conditions of cylinder geometric parameters

网格承力筒在承载力学最优条件下，寻求最小的质量，故将承力筒质量同时作为目标函数。网格承力筒结构参数优化流程，如图7所示。

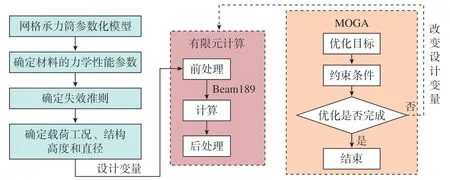
图7 网格承力筒结构参数优化流程Fig.7 Optimization process of cylinder structural parameters

通过多目标遗传算法，获得网格承力筒结构的最优结构参数：螺旋筋缠绕角A为16.625°；螺旋筋旋转角P为17.172°；两端环筋间距H2为129.48mm；中间环筋间距H3～H8分别为129.11mm、115.30mm、119.60mm、127.87mm、 132.91mm和127.53mm。经仿真分析验证发现，该最优工艺参数的最大压应变为3715.8με，最大压应变为1361.2με，最大切应变为3715.9με，不会发生强度失效。优化后结构整体质量为4.423kg，比初始方案降低了约21.2%。

2 优化后结构的屈曲性能分析

网格承力筒的屈曲失效也是其典型失效形式之一，而屈曲失效往往早于强度失效。经过上一部分的论证发现，在现有约束条件下，优化后的网格承力筒不会发生强度失效。为了进一步验证优化后网格承力筒在现有约束下的屈曲性能，对其进行线性屈曲分析，如图8所示。

图8 网格承力筒屈曲模态分析Fig.8 Buckling modal analysis of grid cylinder

由图8可知，网格承力筒X向两侧的螺旋筋屈曲模态振型较大，原因是承力筒上端面受到两种方向载荷的共同作用导致的。网格承力筒一阶屈曲系数为1.774，二阶屈曲系数为1.794，均大于行业抗倾覆标准稳定系数1.5，可见优化后的网格承力筒在现有约束条件下不会发生屈曲失效。

3 网格结构的成型

哈尔滨工业大学数控缠绕机研究所在前期研究的基础上，针对小型回转结构件、卫星网格构件等应用目标，研发出了一套桌面开放式缠绕机控制系统，如图9所示。通过优化后的网格承力筒参数，利用桌面式缠绕机，完成了样件缠绕成型。

图9 自主研发的小型桌面式缠绕机Fig.9 Self-developed of small desktop winding machine

结论

（1）本文采用参数化建模方法，提出网格承力筒环筋与螺旋筋独立设计的思想，减少了两种加强筋之间的耦合作用，使网格承力筒结构设计更为灵活、可控。

（2）在现有工况下，筋条应力以压应力为主。承载性能随着螺旋角的增加呈现先极速下降后缓慢上升的趋势。螺旋角在15°～20°时，筋条最大压应变、筋条拉应变、剪切应变值最小，承力筒承载效率最高。

（3）压应变分析发现，螺旋筋旋转角在单个周期中呈现上升–下降–再上升–再下降的变化特征，最大压应变值在单个周期中不断变化。轴向位移及轴向刚度随螺旋筋旋转角变化呈现先上升后降低的趋势，其中螺旋筋旋转角在约23°时，轴向位移最小，轴向刚度最大。

（4）随着筋条宽度及厚度的增加，最大压应变呈下降趋势。相较于筋条宽度，筋条厚度对承载性能的影响会更大。

（5）优化后的网格承力筒结构，螺旋筋缠绕角A为16.625°、螺旋筋旋转角P为17.172°、两端环筋间距H2为129.48mm、中间环筋间距H3～H8分别为129.11mm、115.30mm、119.60mm、127.87mm、132.91mm和127.53mm。优化后网格承力筒质量比初始方案降低了约21.2%，且不会发生强度失效及屈曲失效。