基于扩展混沌映射的动态身份认证密钥协商协议
2021-07-27曹阳
曹 阳
(陕西理工大学 数学与计算机科学学院,陕西 汉中 723000)
随着互联网技术的发展,网络已经融入到人们生活的各方面,安全问题日益凸显,密钥协商协议的提出就是为用户在公开信道上交换信息提供数据传输的安全性及保密性。Diffie-Hellman[1]于1976年首次提出了密钥协商的概念。由于混沌映射的半群性质及其良好的密码特性与计算性能,基于切比雪夫多项式的混沌映射广泛应用于密钥协商[2-4]中。近年来,研究者针对密钥协商的安全性,基于切比雪夫多项式的混沌映射提出了大量的三方认证密钥协商协议[5-13]:Wang Xing-yuan等[5]提出了一种协商协议,但该协议被E.Yoon等[6]指出是不安全的,存在时间戳、攻击者篡改传输消息不被发现等缺陷;Lai Hong等[7]提出了一个协商协议,但该协议被Zhao Feng-jun等[8]所提出的新的三方密钥协商协议指出存在重放攻击、密钥猜测攻击和不能抵抗内部攻击等缺陷;李雄等[9]提出的三方认证密钥协商协议指出Zhao Feng-jun等[8]的协议不能真正实现用户与服务器之间的相互认证及存在时间戳等缺陷;M.Farash等[10]提出了一个高效安全的三方认证协议,该协议虽然没有使用对称、非对称加密,但计算量大,不能抵抗重放攻击和假冒攻击;Q.Xie等[11]提出了三方口令认证密钥协商协议,但该协议用户不能变更自己的密钥,用户必须与服务器共享密钥才能完成认证与密钥协商;T.F.Lee[12]提出的口令认证密钥协商协议被王彩芬等[13]指出存在内部攻击、不能进行口令更新,且该协议只适用于用户和服务器之间的通信。受上述文献的启发,加之混沌密码学具有较高的安全性和较低的计算复杂度,本文基于混沌映射,针对身份认证密钥协商中的安全性问题,提出了一种基于扩展混沌映射动态身份三方认证密钥协商协议。
1 相关知识
1.1 切比雪夫多项式
定义1切比雪夫多项式[14]
设n为整数,x为区间[-1,1]上的变量,即x∈[-1,1],n维切比雪夫多项式Tn(x)[14]定义为
Tn(x)=cos(n×arccos(x))
(1)
由定义1知,切比雪夫多项式等价递归定义[14]为
Tn(x)=2xTn-1(x)-Tn-2(x)
(2)
其中n≥2,T0(x)=1,T1(x)=x。
性质1半群性质[15]
Tr(Ts(x))=Trs(s)=Tsr(x)=Ts(Tr(x)),r,s∈N;x∈[-1,1]
(3)
Zhang[16]2008年证明了在区间[-∞,+∞]上,切比雪夫多项式仍然具有半群性质。
定义2扩展切比雪夫多项式
设n为整数,x为区间[-∞,+∞]上的变量,即x∈[-∞,+∞],n维扩展切比雪夫多项式Tn(x)定义[16]为
Tn(x)=cos(n×arccos(x))modp
(4)
由定义2知,扩展切比雪夫多项式等价递归定义[16]为
Tn(x)=(2xTn-1(x)-Tn-2(x))modp
(5)
其中n≥2,T0(x)=1,T1(x)=x,p为大素数。
显然,
Tr(Ts(x))=Trs(x)=Tsr(x)=Ts(Tr(x))modp
(6)
1.2 扩展切比雪夫多项式数学难题
设多项式时间内求解以下问题是困难的[16]:
定义3离散对数问题[16]
给定参数x,p,及y=Tr(x)modp,找到一个正整数r,使Tr(x)modp≡y几乎是不可能的。
定义4Diffie-Hellman问题[16]
给定Tr(x)modp,Ts(x)modp及参数p和x,找到一个正整数y,使Trs(x)modp≡y几乎是不可能的。
2 密钥协商协议
协议中包含一个可信服务器S,密钥协商用户Ui、Uj。Ui、Uj需在服务器S的协助下才能协商出一个安全的会话密钥。随机数由随机数发生器生成,用户每次利用随机数发生器生成的随机数都比前一次生成的随机数值大,目的是抵抗重放攻击。协议主要包括注册、密钥协商、密钥更新3个阶段。协议运行前,服务器生成基本参数:大素数p,哈希函数h(),服务器主密钥s,实数z∈[-∞,+∞]。协议中的主要符号如表1所示。
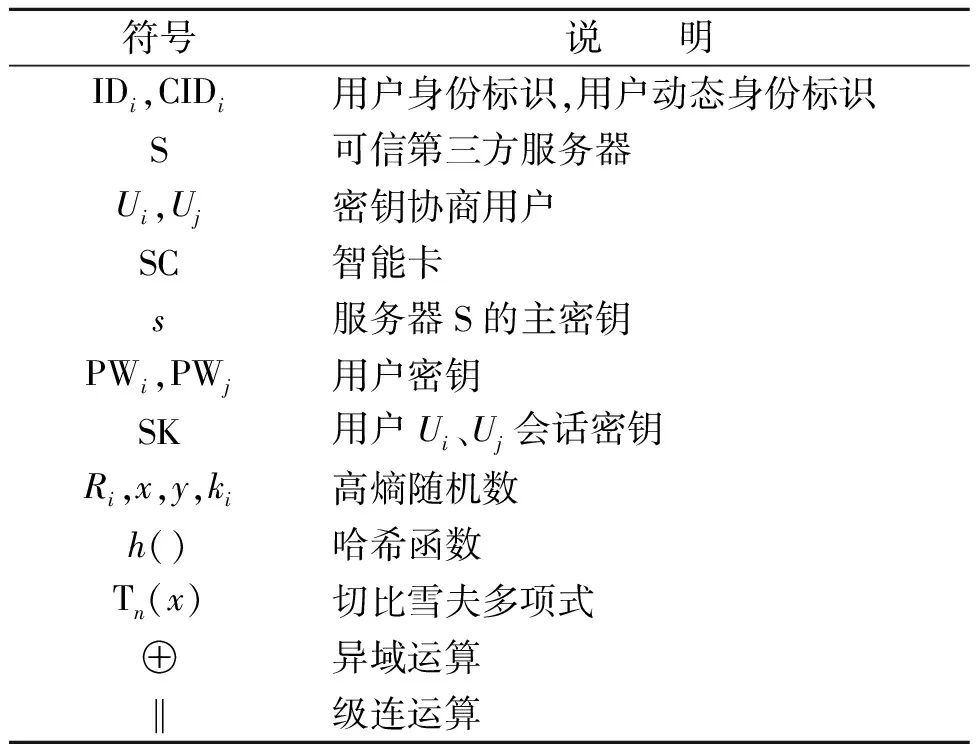
表1 协议中的主要符号说明Table 1 Main symbol description of protocol
2.1 注册阶段
a.用户Ui利用随机数发生器生成一个高熵随机数Ri,输入自己的身份IDi、密钥PWi,计算gi=h(PWi||Ri),并通过安全信道将(IDi,gi)发送给服务器S。
b.服务器S收到 (IDi,gi)后,计算UIDi=h(IDi),并在用户列表中查找UIDi。若找到则说明该IDi已经被注册,拒绝用户的注册请求,并提示用户选取新的身份重新注册;否则,利用随机数生成器生成随机数ki,计算Vi=h(UIDi||s),ei=Vi⊕h(gi||IDi),CIDi0=h(UIDi||ki),SV=Ts(z)modp,将(UIDi,CIDi0)添加到用户列表,并将(CIDi0,h(),ei,SV,p,z)存入智能卡SC,最后将SC通过安全信道发送给用户Ui。
c.用户Ui收到智能卡SC后,输入IDi,PWi,计算Ei=h(IDi||PWi||gi)(ei⊕h(gi||IDi),Ki=h(IDi||PWi||Ei),用Ei替换SC中的ei,并将Ki和Ri存入SC中。注册过程如图1所示。

图1 用户注册过程Fig.1 User registration process
2.2 密钥协商阶段
设用户Ui和Uj进行通信,密钥协商执行如下操作
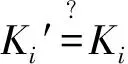

c.S收到消息{CIDi0,CIDj0,C1,d1,R1,C3,d2,R2}后,首先在用户数据库中查找CIDi0和CIDj0,若找不到则拒绝用户登录请求,否则取出CIDi0对应的UIDi′,CIDj0对应的UIDj′,计算Vi′=h(UIDi′||s),Vj′=h(UIDj′||s),
C2′=Ts(C1)modp=Ts(Tx(z))modp
=Tx(Ts(z))modp=Tx(SV)modp,
C4′=Ts(C3)modp=Ts(Ty(z))modp


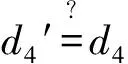
e.S收到消息d5、d6后,计算d5′=h(CIDi0||CIDi1||Vi′||R1),d6′=h(CIDj0||CIDj1||Vj′||R2),若等式d5′=d5和d6′=d6成立,则将用户数据库中的CIDi0更新为CIDi1,CIDj0更新为CIDj1。密钥协商过程如图2所示。
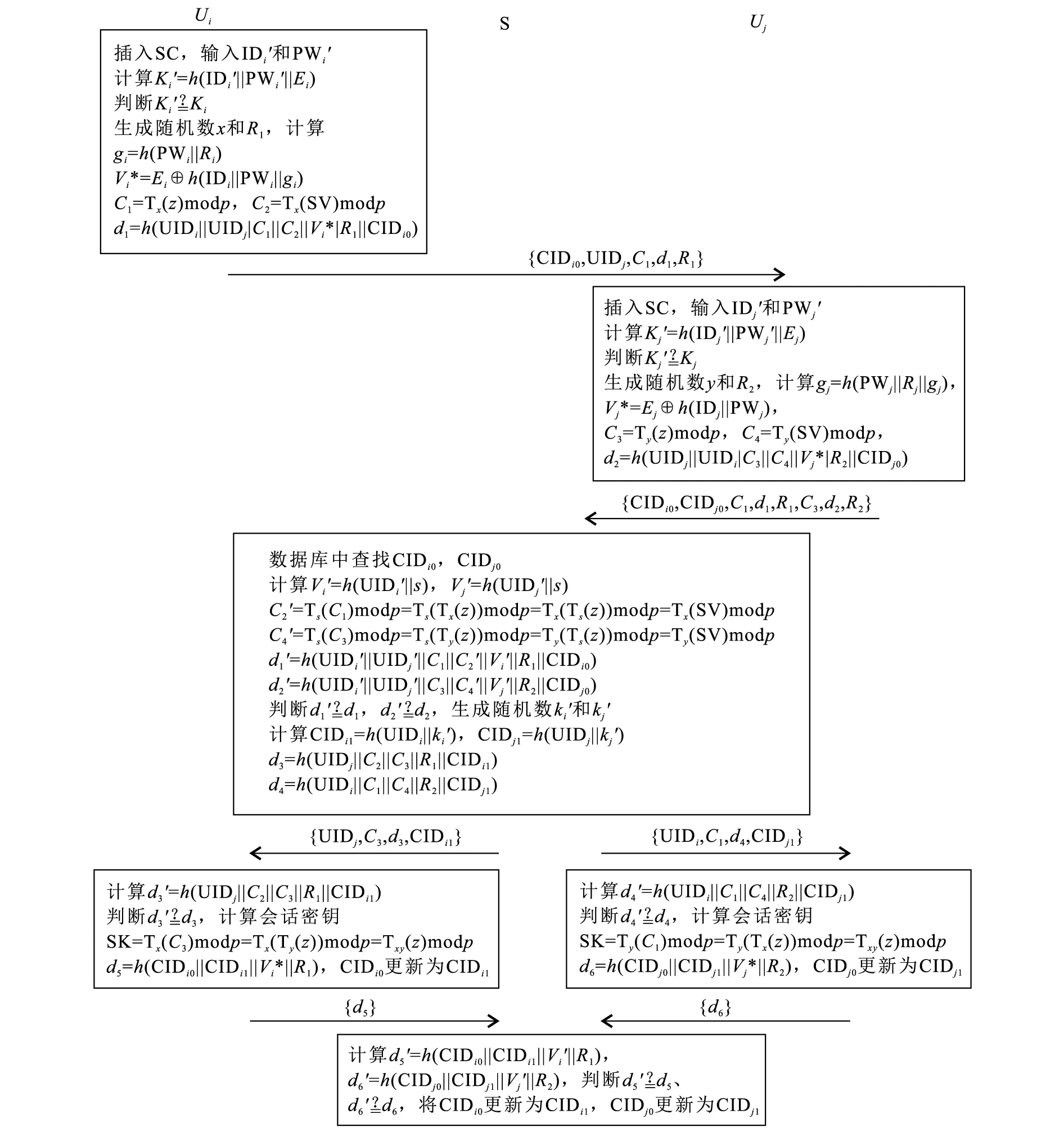
图2 密钥协商过程Fig.2 Key agreement process
2.3 密钥更新阶段
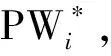

3 协议分析
3.1 安全性分析假设
假设1协议中使用的哈希函数h()、服务器的主密钥s是安全的。也就是说攻击者在多项式时间内解决这些问题是不可能的。
假设2攻击者已锁定目标用户,并能在安全信道上截取目标用户与服务器之间、目标用户之间的通信信息,否则由于用户每次登录的身份不同,使得攻击者即使得到了相关信息,攻击都是无效的。
3.2 安全性分析
a.用户匿名性

b.提供相互认证
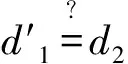
c.抗密钥猜测攻击
协议中,如果攻击者截获了服务器S与用户Ui之间传递的信息,则他可以发起密钥猜测攻击。根据SK=Tx(C3)modp=Tx(Ty(z))modp=Txy(z)modp、{UIDj,C3,d3,CIDi1}知,x是用户选取的随机数,y并没有包含在传递信息{UIDj,C3,d3,CIDi1}中,而是隐藏在C3中;即使攻击者获得了用户Ui与服务器S之间传递的信息,由扩展切比雪夫多项式的离散对数问题及Diffie-Hellman问题知,攻击者无法获得x、y,也就无法计算出会话密钥。
d.抗冒充攻击
协议中,用户登录、密钥协商的身份是动态身份,且每次认证成功后都会修改下次登录的身份。如果攻击者重放以前或本次经过双方认证后的消息,则很容易被服务器S识破。
1)假设攻击者冒充用户Uj,尝试构造消息{CIDi0,CIDj0,C1,d1,R1,C3,d2,R2},由于上次用户密钥协商后,服务器S已经更新了用户下次登录的动态身份CIDi0为CIDi1、CIDj0为CIDj1,服务器S在用户数据库中查找,找不到CIDi0、CIDj0而拒绝登录请求,攻击者冒充用户失败。
2)假设攻击者冒充服务器尝试构造消息{UIDj,C3,d3,CIDi1}、{UIDi,C1,d4,CIDj1}发送给用户。当用户收到消息后,将计算d3′、d4′来实现对服务器的认证。由d3=h(UIDj||C2||C3||R1||CIDi1)、d4=h(UIDi||C1||C4||R2||CIDj1)知,d3、d4中含有随机数,而用户每次登录时选择的随机数不同,攻击者无法通过用户的认证。
e.抗重放攻击
1)假设攻击者冒充用户Uj成功重放消息{CIDi0,CIDj0,C1,d1,R1,C3,d2,R2},即攻击者通过了服务器S的认证,并将消息{UIDj,C3,d3,CIDi1}发送给Ui、{UIDi,C1,d4,CIDj1}发送给攻击者。由C1=Tx(z)modp、C3=Ty(z)modp、SK=Tx(Ty(z))modp=Txy(z)modp知,攻击者要想计算出正确的会话密钥,他必须知道Tx、Ty,而x和y都是用户选取的随机数,在不知道随机数x和y的情况下,攻击者计算必须面临扩展切比雪夫多项式离散对数问题和Diffie-Hellman问题,所以攻击无法成功。

3)假设攻击者截取了服务器S发送给用户Ui的消息{UIDj,C3,d3,CIDi1},然后重放消息{UIDj,C3,d3,CIDi1}。由C3=Ty(z)modp、d3=h(UIDj||C2||C3||R1||CIDi1)、SK=Tx(C3)modp=Tx(Ty(z))modp=Txy(z)modp知,攻击者必须知道用户Ui已有的C2、R1才能确认用户Uj的身份,同时他还必须知道随机数x和y,才能计算出会话密钥SK,所以攻击不会成功。
f.抗窃取智能卡攻击
假设攻击者窃取到合法用户智能卡中存储的信息(CIDi0,h(),Ei,SV,p,z,Ki,Ri},但当他想冒充合法用户与其他用户进行密钥协商时,他必须输入正确的身份和密钥,由智能卡计算Ki′,并与智能卡中Ki相比较,只有比较相等,智能卡才会继续计算相关信息,执行密钥协商协议。由于攻击者无法输入正确的用户身份和密钥,所以即使窃取了智能卡的信息,也无法冒充合法用户。
g.抗已知会话密钥攻击
由2.2节密钥协商知,会话密钥SK=Tx(Ty(z))modp=Txy(z)modp,其中x、y是每次密钥协商时用户选取的随机数,攻击者即使知道了上次会话密钥,也无法推断出本次会话密钥,即已知会话密钥攻击失败。
h.完美前向安全性
协议中,双方协商会话密钥为SK=Tx(C3)modp=Ty(C1)modp=Txy(z)modp。设攻击者通过公开信道获取了C1、C3,且知道Tx、Ty。若攻击者想从Tx、Ty计算出x、y,则面临扩展切比雪夫多项式离散对数问题;若攻击者直接由Tx、Ty计算出Txy,则面临扩展切比雪夫多项式Diffie-Hellman问题。所以本协议的会话密钥具有完美前向安全性。
i.抗内部攻击
实际应用中,用户可能会使用同一个身份及密钥与不同的服务器间进行交互,那么用户的身份及密钥存在可能被内部人员利用的风险。本协议中,用户注册时传递的信息不是直接发送的,而发送的是(IDi,gi),gi=h(PWi||Ri),即通过哈希函数和随机数将用户的密钥进行隐藏,对任何内部人员,gi只是一个哈希函数值,所以本协议可以抵抗内部攻击。
3.3 安全性比较
根据以上的安全性分析结果,下面从用户匿名性、抗冒充攻击、抗重放攻击、相互认证、抗内部攻击、抗已知会话密钥攻击、抗密钥猜测攻击、抗窃取智能卡攻击、完美前向安全性、系统主密钥更新等方面与文献[5,7-8,10-11]进行安全性比较。安全性比较结果如表2所示,其中“Y”表示具备该安全性,“N”表示不具备该安全性。

表2 安全性比较Table 2 Security comparison
3.4 效率分析
表3列举了本协议与文献[5,7-8,10-11]计算效率的比较结果,其中tC表示执行一次切比雪夫多项式所需的时间,tH表示执行一次哈希函数所需的时间,tS表示执行加/解密所需的时间。协议中由于异或运算的计算量较少,在进行计算量比较时忽略不计。

表3 计算效率比较Table 3 Comparison of computational efficiency
由于协议中主要运算在密钥协商阶段,所以表中对密钥协商阶段计算效率进行比较。由文献[17-18]知,tC≈2.5tH,tC≈70tS≈175tH。在3.2 GHz处理器3.0 G RAM环境下,tH的执行时间为0.2 ms。从表3比较结果可以看出,本协议计算执行时间需要283.6 ms,计算效率明显优于文献[5,8,11],与文献[7,10]相当。但本协议不存在加密/解密算法,不存在时间戳,且只有服务器和用户之间相互认证后,才更新用户的身份,所以安全性更高。
4 总 结
本文基于混沌映射的半群性质及其良好的密码特性,提出了基于动态身份可认证的密钥协商协议。密钥协商用户每次登录认证的身份都不同,并在可信的第三方服务器的帮助下实现了用户间的双向认证和密钥共享功能。通过用户密钥和系统主密钥便捷的更新方法增强了协议的安全性。从安全性和性能分析,及其与相关文献的比较结果可以看出,本文的协议具有较高的计算性能,能抵抗常见攻击,具有完美的前向安全性。因此,该协议更适用于网络受限的实际应用环境。
