光机械系统中弱测量的放大效应
2021-07-27李刚
李 刚
(延安大学 物理与电子信息学院, 陕西 延安 716000)
0 引 言
1988年,弱测量理论由Aharonov等[1]提出,通常被称之为弱值放大机制。目前,弱测量已成为最有前途的精密测量工具之一,它已应用于各个研究领域,包括解决量子力学中的基础问题[2-3]和解释一些违反直觉的量子悖论[4]。在弱测量中,指针弱耦合到被测量的系统。与投影测量对比,若指针的初始波函数的宽度很大,则在弱测量中指针的输出信号,指针观测量的值会远远超出系统观察量的特征值的范围,这个结论归因于指针的量子态叠加量子干涉效应。当被测量的系统发生接近正交的后选择后,指针的两个或多个稍微不同的平移高斯态的叠加[1,5]可以给出系统观察量的值超出其特征值的范围。最近发现,弱测量可以帮助测量较小的物理量[6]或对较小的物理参数进行灵敏地估计[7-11],然而传统技术很难直接检测到它们。大多数弱测量方案都可以通过经典波动力学来解释[12]。此外,更多有关弱测量领域的评论可以参见文献[13-14]。
尽管弱测量在光学领域被广泛应用,但其在光力学领域的应用还不是很多[15-18]。笔者从相干态指针入手对量子弱测量放大进行详细的讨论,试图找到有关弱测量的一种新放大机制,以及在结合弱测量的光机械系统中是否存在一些新颖量子效应。
1 弱测量放大原理
文中使用马赫曾德干涉仪模拟弱测量的方法研究光机械系统中弱测量放大效应。光机械系统装置如图1所示。
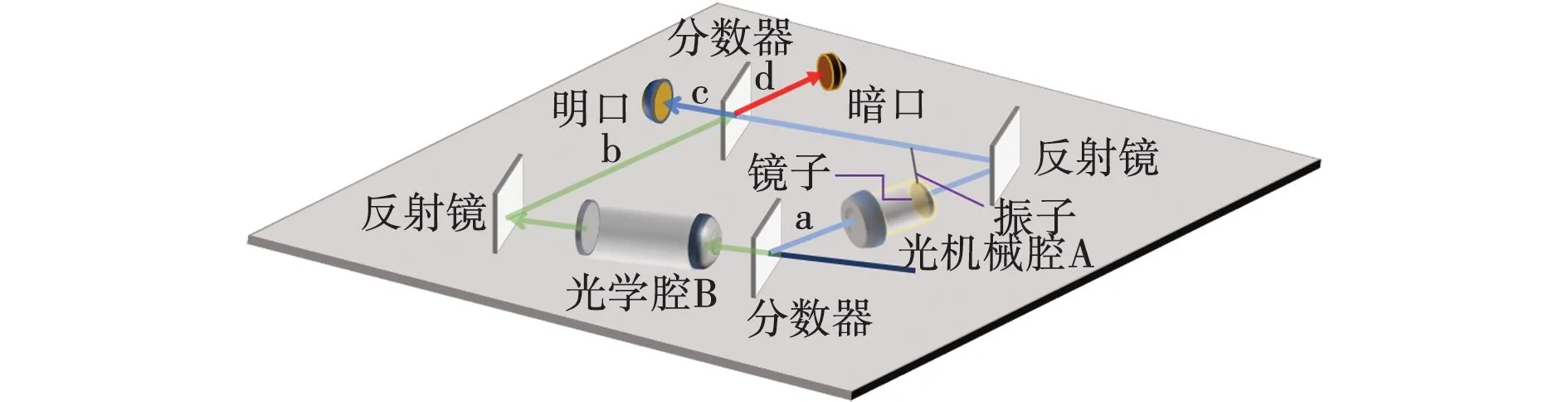
图1 光机械系统装置Fig. 1 Optomechanical system device
光机械腔A被放置在马赫曾德干涉仪的一个臂上,并将常规光学腔B放置在干涉仪的另一个臂上。两个分束器(BS)都是对称的,整个系统的哈密顿量的表达式[15-17]为
(1)

ω0——光学腔模A、B的角频率;
a1、a2——光学腔模A、B的湮灭算符;
b——角频率为ωm的机械模的湮灭算符;
g——光机械耦合强度,g=ω0σ/L;
L——光学腔的长度;
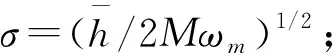
M——机械振子的有效质量。
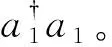
假设镜子初态被制备在相干态|α〉m,α=|α|expiθ,其中|α|和θ都是实数,分别称之为相干态的振幅和相位[19]。经式(1)的弱相互作用后,整个系统(被测系统和指针)的时间演化是与处于相干态的镜子微弱相互作用之后,整个系统的状态变为
|ψsm(t)〉 =U(t)|ψi〉|α〉m,
(2)
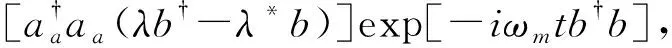
(3)
式中:φ(t)——克尔项的时间,φ(t)=k2(ωmt-sinωmt);
λ(t)——平移项的时间,λ(t)=k(1-e-iωmt);
k——缩小比例的光机械耦合参数,k=g/ωm。
对式(3)进行简化,得

(4)
式中:|ψ(λ,φ,t)〉——单光子作用的镜子演化态,|ψ(λ,φ,t)〉=eiφ(t)D(λ)|φ(t)〉m;
φ——无光子作用的镜子演化态,φ=αe-iωmt;
D(λ)——一个平移算符,D(λ)=exp[λb†-λ*b]。
当在暗口检测到光子时,用弱测量语言来说后选择发生,即对单光子系统进行了投影测量,投影算符|ψf〉〈ψf|,则镜子的最终状态变为
|Ψm(t)〉=〈ψf|ψsm(t)〉 =(|ψ(λ,φ,t)〉m-
|φ(t)〉m)/2,
(5)
为了进一步简化分析,利用定义式 |χm(t)〉=D†(φ(t))|Ψm(t)〉,即平移等式(5)的态到相空间原点,获得
|χm(t)〉=(exp[iφ(t)+iφ(α,t)]|ξ(t)〉m-|0〉m)/2,
(6)
其中,exp[iφ(t)+iφ(α,t)]是相干态|λ〉m和基态|0〉m之间的相对相位。而φ(α,t)=-i[(λφ*-λ*φ)]是通过两个不同的平移算子非对易性质,
(7)
由式(7)可知,两个镜子态之间的相对相位是由量子力学中非对易性[20-21]引起的。文献[15]中,正交后选择发生后两个镜子态之间的相对相位可以导致弱测量放大效应。
将给出如何通过该相对相位exp[iφ(t)+iφ(α,t)]来产生镜子微弱动量,类比于经典动量等于质量乘以速度的放大。换一句话说,镜子质量不变,速度能通过弱测量放大变快。
2 相干态对动量p放大的影响
2.1 相干态指针对动量p放大的影响
在弱测量中,镜子(机械振子)上动量p的平均平移为
(8)
将式(6)代入式(8),得
(exp[iφ(t)+iφ(α,t)]λ(t)-exp·
[-(iφ(t)+iφ(α,t))]λ*(t))]/
[2σ(2-exp[-|λ(t))|2/2](exp[iφ(t)+
iφ(α,t)]+exp[-(iφ(t)+
iφ(α,t))])]。
(9)
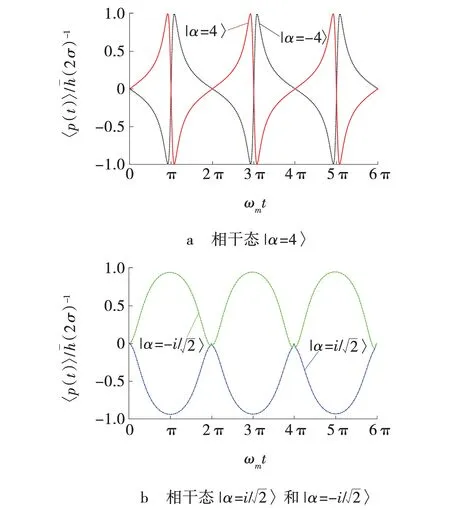
图2 镜子的动量平均位移Fig. 2 Average momentum displacement mirror
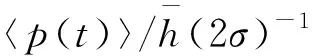
接下来,分析相对相位是怎么使镜子的微弱动量放大。
2.2 动力学演化时间对放大效应的影响
为了探讨在ωmt=π附近发生的放大效应,对于式(6),在时间ωmt=π处进行泰勒展开,保留到第一阶。假设|ωmt-π|≪1和k≪1,则
|χm(t)〉 ≈ [2k|1〉m+i2k|α|(2sinθ-
(ωmt-π)cosθ))|0〉m]/2。
(10)

3 耗散对动量p放大效应的影响
文中仅考虑零温条件下的耗散,因此,机械系统的主方程[21,23]为
c†cρ(t)-ρ(t)c†c]/2,
(11)
式中,γm——阻尼常数。
阻尼噪声对镜子放大效应的影响如图3所示。通过式(11)给出光机械系统的耗散演化解析解或者数值解,与无耗散条件的式(9)进行对比可知,在零温条件下阻尼噪声对弱测量放大的影响。
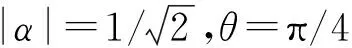
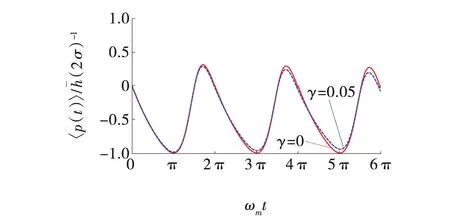
图3 阻尼噪声对镜子的放大效应影响Fig. 3 Influence of damping noise on amplification effect of mirror
文中所给的方案需要单光子源,并且它成功的选择后概率非常低。众所周知,制备理想单光子的条件非常苛刻,经济成本很高[25],这些方案[15,18]在单光子条件下是很难通过实验验证的。最近,利用弱相干光代替单光子的弱测量方案被提出[26],表明单光子情况下的微弱动量放大可以通过弱相干光来实现,其成功的后选择概率也变大,因此,这个方案在目前实验条件下是可行的。根据量子力学不确定性原理,不可能同时测量镜子的位置和动量。 但是,可以以任意精度测量机械运动的一个正交分量[27](例如动量)。这个方法可以用来完全重构机械振子量子态,并使用量子态层析技术提取其威格纳函数密度[28],从而给出相空间的动量分布。
4 结 论
(1)当镜子处于相干态时,镜子动量的平均平移的最大放大值可以在ωmt=π附近发生,并可达到基态的零点涨落,当镜子处于基态时[1,5,7-11],不难发现,放大效应不会出现。
(2)后选择测量后,指针态之间的相对相位是由量子力学中非对易性引起的,这是一种弱测量放大的新机制,与标准弱测量放大机制不同[1,5],后者是通过对被测系统的后选择(对被测系统进行投影测量)获得相对相位。
文中所给的方案在目前实验条件下是可行的实验方案。这些结果不但扩展了弱测量在光学机械系统中的应用,也加深了人们对弱测量的理解。
