太阳能热气流发电系统导流体的模拟和实验研究

2021-07-26陈举胜王海霞李洪松刘宇飞李庆领

青岛科技大学学报（自然科学版） 2021年4期

陈举胜,王海霞,李洪松,刘宇飞,李庆领

(青岛科技大学机电工程学院,山东青岛 266061)

太阳能热气流发电系统的理念最早由CABANYES[1]在1903年所提出,世界上第一座实验型太阳能热气流发电系统于1982 年在西班牙Manzanares成功建造,主要结构包括集热棚、烟囱和透平装置,产电量可达50 k W[2]。基于此,研究者不断进行深入研究,取得了诸多的研究成果。蔡琦龙等[3]对定面积下的集热棚倾角进行研究,表明太阳能热气流发电系统的性能会随着倾角的增加先提高后减小;朱海林等[4]分析计算了集热棚半径与棚内气流速度、对流换热系数以及集热棚内部吸热效率的关系;黄慧兰等[5]分析研究了不同烟囱的高度、直径和倾角对烟囱效率的影响,烟囱高度和直径的增大会提高烟囱的效率,倾角在增大到某个极值时烟囱效率便基本不再发生变化;FLURI等[6]对涡轮机不同配置进行研究,得出单垂直轴涡轮机效率优于其他配置的结论。

随着对系统结构的不断研究,研究者发现太阳能热气流发电系统内部导流结构会对系统的效率产生影响。彭维等[7]对烟囱进口流道进行优化,从而提升了烟囱进口处的风速;MING 等[8]通过对西班牙原型的模拟,发现在烟囱底部增设导流体会对局部的相对静压和速度产生十分显著的影响,从而可以增加太阳能烟囱发电厂的输出功率;HU 等[9]对烟囱底部同一形状,但不同长径比的导流体进行了模拟研究,模拟显示最佳长径比的导流体对烟囱内部流场有着明显的改善作用。

目前关于导流体的研究是基于烟囱底部流场特性进行定性分析,并取某一截面上单一速度进行功率计算,而单一点的选取计算会出现较大误差。因此本工作在诸多学者对导流体研究的基础上,结合等效速度理论,提出一种新型等效速度面划分方式,计算分析了不同形状导流体对太阳能热气流发电系统输出功率的影响,结合压力场进一步比较不同形状导流体对流动特性的影响。

1 实验系统

太阳能热气流发电系统主要由集热棚、蓄热层、烟囱、透平装置和导流体组成。系统通过集热棚和蓄热层对太阳能进行吸收和储存,以期能持续对棚内空气进行加热。空气受热密度减小,不断上升,经导流体引流后进入烟囱。烟囱具有抽吸作用,进一步加强空气流速,推动烟囱内部的透平装置进行发电作业。

根据Manzanares太阳能热气流发电系统实验装置尺寸[2],按照100∶1比例尺,搭建一座小型太阳能热气流发电系统实验台,如图1所示。

实验台烟囱高度为2 000 mm,直径200 mm,材质为亚克力;集热棚直径为2 400 mm,棚外沿与水平地面的倾角为8°,距离水平地面的高度为60 mm,材质为PC耐力板;实验装置的整体框架采用方管焊接,集热棚下方区域为土壤。

实验装置的集热棚入口处和烟囱底部均布置有TES-1341热线风速仪,以测量气流风速。集热棚与蓄热层均匀分布不同的测点,如图2所示。图2(a)中,测点沿集热棚横向等间距分布,选用T 型热电偶测量温度,数据利用Agilent进行采集,每次采集间隔20 s,最后取其平均值作为该点温度。图2(b)中,ai(i＝1,2,3,4,5)距土壤中心点O 的距离H1为200 mm,bi(i＝1,2,3,4,5)距土壤中心点O 的距离H2为600 mm,ci(i＝1,2,3,4,5)距土壤中心点O 的距离H3为1 000 mm,利用TES-1310数字式温度表蓄热层上不同测温点进行温度测量。集热棚内外的太阳能辐射强度则通过TES-1333太阳能辐射仪在同一时刻多次测量,并取其平均值。

图2 测温点示意图Fig.2 Schematic diagram of temperature measurement point

实验装置所采用的仪器中,TES-1341热线风速仪量程为0.1～30.0 m·s－1,分辨率为0.01 m·s－1,误差为3%;TES-1310 数字式温度表量程为－50～1 300 ℃,分辨率为0.1 ℃,当测温范围在－50～199 ℃时,误差范围在0.1～1.398 ℃;T 型热电偶量程为－200～350 ℃,数据采集仪精度为6位数,连接热电偶时测量准确度为1℃,其温度系数为0.03 ℃;TES-1333 太阳能辐射仪档位为2 000 W·m－2,分辨率为1 W·m－2,误差为5%。

2 等效速度

太阳能热气流发电系统依靠烟囱底部安装的涡轮机组进行发电,集热棚内热气流上升会带动涡轮机工作进行发电,但仅取某一点速度进行计算会导致计算功率与实际功率有较大的偏差。文献[10-11]提出等效速度理论,利用等效速度计算输出功率会大大降低与实际功率的偏差。太阳能热气流发电系统烟囱内部气体的流动速度大小呈近似圆形的均匀分布,基于此,对于等效速度面的划分,本研究提出一种同心圆式的划分方式,如图3 所示。其中,A1～AN代表每个圆环的面积,U1～UN表示各个圆环平均速度,圆环划分数量越多,计算结果越精确。

假设风力方向垂直于叶轮,不考虑其他影响,等效速度计算公式[12]为

其中:Ueq,等效速度;A,等效速度面面积;,各个圆环的平均速度;Ai,各个圆环的面积。

因此,等效速度预测叶轮输出功率的公式为

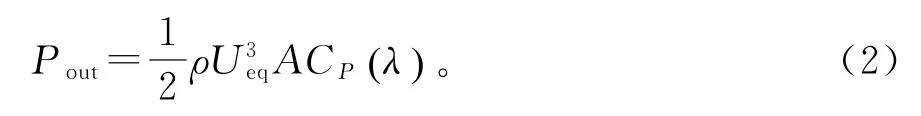
其中:Pout,叶轮输出功率;ρ,密度,气流密度ρ 为1.05 kg·m－2;CP(λ),叶尖速比λ 下的叶轮功率系数,根据文献[13]中所提出的设计条件,叶轮功率系数CP(λ)为0.482。

3 数值模拟

3.1 物理模型

基于西班牙Manzanares试验电站的实际尺寸,建立物理模型,主要结构参数如表1所示。

表1 物理模型中主要的结构参数Table 1 Main structural parameters in the physical model

导流体安放在烟囱的正下方,高度设置为12 m,底面半径设置为8 m。圆锥导流体如图4(a)所示,是一种曲面圆锥的导流体,其曲面分别切于曲面圆锥的顶点和底面。圆台导流体如图4(b)所示,是一个曲面圆台的导流体,其曲面切于上底面,且上底面半径为1 m。圆顶导流体如图4(c)所示,是顶部为半球形的圆台导流体,球形的半径为1 m,其曲面切于半球面,总高度仍为12 m。

图4 3种形状的导流体的三维图Fig.4 Three-dimensional map of three shapes of the diversion

3.2 数学模型及边界条件

对太阳能热气流发电系统的数学模型进行以下假设:环境温度保持不变;集热棚内的辐射强度保持不变且均匀分布;土壤表面保持恒温且均匀分布;除辐射强度和土壤温度无其他热源。

太阳能热气流发电系统的气体流动是一种自然对流状态,自然对流条件下的流体流动状态是基于瑞利数Ra 进行判断[14]。

瑞利数:

其中:β,热膨胀系数;ΔT,系统内温差;L,特征长度;g,重力加速度;ν,运动黏度;α,热扩散系数。

当瑞利数大于1010,即认为流体是属于湍流流动,经分析计算,在太阳能热气流发电系统中,气体的流动应属于湍流流动。

因此,模拟中使用的控制方程如式(4)～式(6)。

其中:U,速度矢量;ui,x,y,z 方向上的速度分量。

依据数学模型并结合相关文献[15],设置如下边界条件:1)集热棚为热通量壁面条件;2)土壤表面为恒温壁面条件;3)集热棚入口为压力入口,烟囱出口为压力出口,进出口相对压强均为0 Pa,环境温度为15 ℃;4)其余壁面均为绝热壁面。

4 结果分析

4.1 速度场分析

为避免网格数量带来的偶然性,采用多种不同数量的网格进行模拟计算,计算结果取导流体正上方2 m 处作为等效速度面,速度云图如图5所示。

图5 等效速度面处不同形状导流体的速度云图Fig.5 Velocity cloud map of different shape of the diversion at the equivalent velocity plane

从图5可以看出,在等效速度面处,无导流体和3种不同形状导流体的速度分布呈现近似的同心圆分布。无导流体时,靠近烟囱壁面处速度最小,速度向烟囱中部逐渐增大,仅在局部地方出现高速度的现象,增设导流体后,速度沿着烟囱壁面至烟囱中部先增大后降低,圆锥导流体速度分布最为规律均匀,并无明显高速度区域,越靠近烟囱中部,圆台导流体速度降低越明显。该速度分布规律是由于受热空气沿烟囱底部进入时,受导流体形状影响,流动特性会随之发生不同的变化。导流体会减少烟囱底部的节流面积,增强抽吸作用,但同时会在导流体正上方形成一个低速区域,造成速度沿烟囱内壁向烟囱中部速度先增后减的现象。

基于同心圆式的划分方式,结合等效速度面处的速度云图,将等效速度面均匀划分成20个圆环,从烟囱壁面至烟囱中部依次划分为圆环1 至圆环20,每个圆环均匀取12个点进行平均速度的计算,不同形状导流体各圆环平均速度分布如图6所示。

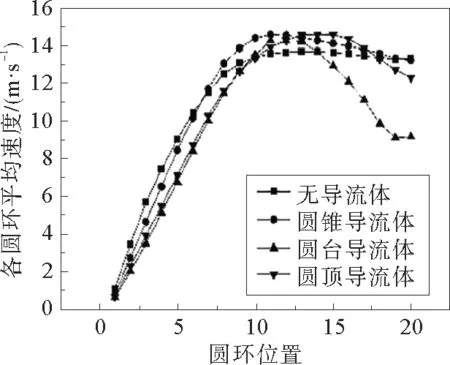
图6 不同导流体各圆环平均速度分布Fig.6 Average velocity distribution of each ring of different shape of the diversion

从图6可以更准确看出,等效速度面处,不同导流体速度分布沿着烟囱内壁向烟囱中部呈现先增大后减小的趋势,将圆环1至10定义为低速区,圆环11至20定义为高速区。低速区内,气体速度不断提高,变化剧烈。高速区内,无导流体时最大和最小平均速度分别为13.652、13.289 m·s－1,变化幅度为2.7%。圆锥导流体速度最大和最小平均速度分别为14.557、13.193 m·s－1,变化幅度为9.4%。圆台导流体速度最大和最小平均速度分别为14.228、9.091 m·s－1,变化幅度为36.1%。圆顶导流体速度最大和最小平均速度分别为14.577、12.274 m·s－1,变化幅度为15.8%。

速度场分析结果表明:无导流体时烟囱内部气体在高速区的流动最为稳定,但平均速度较低。增设导流体后,圆锥导流体平均速度下降幅度最低,圆台导流体平均速度变化幅度最为明显。

4.2 输出功率

基于等效速度,结合速度场分析结论,分别计算等效速度面和高速区的等效速度和输出功率,设置不同形状导流体后等效速度及输出功率如表3所示。

由表3可知,不同形状导流体对等效速度以及叶轮输出功率的影响程度不同,高速区内叶轮输出功率较等效速度面处显著提升,无导流体时增幅最低,为48.2%,设置圆锥、圆台或圆顶导流体时增幅分别为50.4%、62.5%和57.2%。以无导流体时的等效速度和输出功率作为基准,当叶轮分布于整个等效速度面时,圆锥导流体等效速度较无导流体时增加了3.3%,输出功率提高9.6%;圆台导流体等效速度较无导流体减少了5.9%,输出功率则降低16.6%;圆顶导流体的等效速度较无导流体时减少了1.9%,输出功率则降低5.7%。

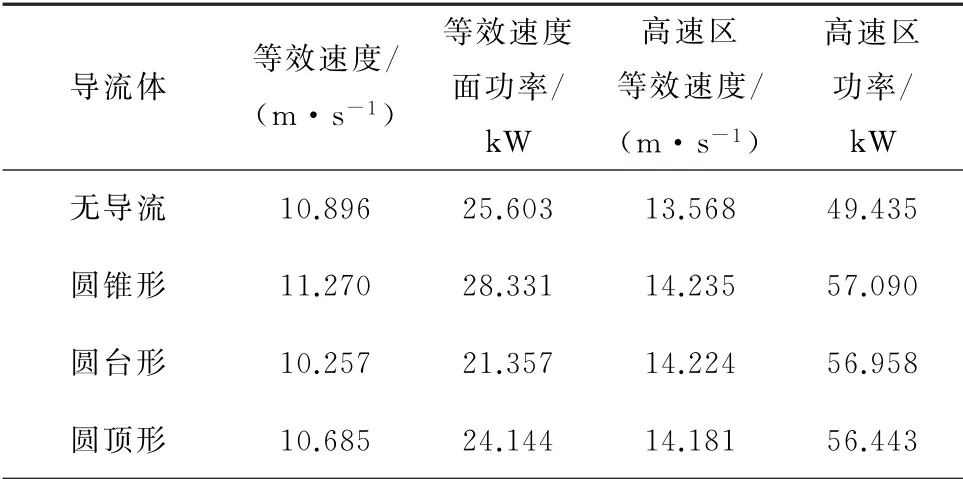
表3 不同形状导流体等效速度以及输出功率Table 3 Equivalent velocity and output power of different shapes of the diversion

当叶轮仅分布在高速区时,3种导流体对等效速度和输出功率的促进作用最为明显。圆锥导流体等效速度较无导流体时提升4.7%,输出功率提高13.4%;圆台导流体等效速度较无导流体提升4.6%,输出功率提高13.2%;圆顶导流体的等效速度较无导流体时提升4.3%,输出功率提高12.3%。

从数据对比中可以得出,当叶轮扫掠的面积占据整个等效速度面时,增设导流体的提升效果十分有限,圆台和圆顶导流体甚至引起反作用。若叶轮大小不超过高速区范围,无导流体的等效速度和输出功率虽大幅增加,但导流体的促进作用则更为显著,对系统的增幅效果都优于无导流体时,以圆锥和圆台导流体的提升效果最佳。

4.3 压力场分析

太阳能热气流发电系统中烟囱的抽吸作用会进一步增加受热气体动能,以此提升对叶轮的驱动作用,取XOY 面作为基准面,图7为不同形状导流体在烟囱底部的压力分布云图。

由图7可见,增设导流体后,烟囱底部的相对压力值均有不同程度的降低,负压值增大,增大的负压值会加强烟囱的抽吸作用。最大负压值出现在烟囱底部壁面处,主要是由于烟囱壁面与集热棚的连接处未进行倒角处理,受热气体进入烟囱时,在其周围形成较大的负压区域。不同形状的导流体中,圆锥导流体负压增幅最低,为11.8%,圆台导流体负压增幅最高,为21.1%。

图7 不同形状导流体在烟囱底部的压力分布云图Fig.7 Pressure distribution cloud diagram of different shape of the diversion at the bottom of the chimney

综上所述,不同形状导流体对太阳能热气流发电系统的提升程度不同,圆锥导流体对等效速度和输出功率的提升效果最佳,圆台导流体与之相近,圆顶导流体提升程度最小。不同形状导流体在烟囱底部负压变化不同,圆台导流体明显高于圆锥和圆顶导流体。现实中安装叶轮时,考虑到经济性和安装难易度,应选用圆台导流体作为太阳能热气流发电系统中烟囱底部的导流装置。

4.4 实验对比

利用3D 打印技术制作相应尺寸的圆台导流体进行实验和模拟的对比验证。由于小型实验台的局限性,在进行对比验证时,物理模型按照实验台尺寸进行1∶1绘制。实验时集热棚入口处风速会随着环境风的变化而不断发生变化,故而对入口边界条件采用不同的风速入口,其余边界条件不变,实验与模拟结果如图8所示。

图8 实验结果与模拟结果对比Fig.8 Comparison of experimental and simulated data

根据图8可知,模拟结果中的烟囱底部处风速随着集热棚入口风速的增加而均匀增加,实验结果中的烟囱底部处风速的增加则出现一定的波动,但两者在烟囱底部处的速度都呈现出随集热棚入口风速的增加而增加的趋势。但是两者在烟囱底部处风速增加的趋势基本保持一致,风速大小也较为接近。模拟所获取的平均最高温度为301 K,实验所获取的最高平均温度为294 K,两者分布均靠近烟囱底部处,最低平均温度均出现集热棚入口处。在实验和模拟中,集热棚入口处外部空气不断输入,导致入口整体温度偏低。越靠近烟囱底部处,气体换热充分,温度升高,沿烟囱底部产生上升气流,带动涡轮机发电。烟囱底部气体流动性高,使其温度低于集热棚内部的气体温度。

考虑到室外实验环境风速的不可控性和测量误差,模拟所设定的边界条件是稳定的入口风速、太阳能辐射强度以及土壤表面的温度,造成了实验和模拟结果存在一定的差距,但系统内气体流动特性与变化趋势基本一致,可以验证模拟可靠性。