基于重叠网格法的斜拉索涡激振动分析
2021-07-26王贵春曹宗恒
王贵春,曹宗恒
(郑州大学 土木工程学院 河南 郑州 450001)
0 引言
涡激振动是由结构尾流区漩涡脱落引起的结构周期性振动,具有强迫、自激及限幅的特点。斜拉索在流体作用下都可能发生涡激振动,从而导致结构疲劳破坏,影响结构正常使用。所以研究斜拉索涡激振动响应特性具有重要意义。
Feng[1]在1968年进行风洞试验,研究了单圆柱体涡激振动响应。随着计算机技术的迅速发展,很多学者采用计算流体动力学(compute fluid dynamics,CFD)方法研究圆柱体涡激振动响应特性。李广望[2]采用任意Lagrange-Euler方法计算了圆柱体的涡激振动响应。徐枫[3]采用动网格技术对不同截面形式的柱体进行了数值模拟,但是柱体运动引起的计算网格畸变、缠绕等问题不能得到有效解决。刘志文等[4]采用“刚性区域+动网格区域+静止网格区域”的方式建立网格,对矩形断面桥梁涡激振动进行计算,计算过程中虽能保证壁面附近计算网格的质量,但是运动网格划分方式较复杂且不同划分方式网格间的连接容易出现问题,尤其是当网格出现变形时,动网格区域计算网格质量大幅下降,容易影响计算结果的精度。刘军[5]采用Fluent对高雷诺数下输电导线涡激振动进行了分析,并详细分析了高质量比和低质量比参数对涡激振动的影响,其研究结果表明:低质量比涡激振动振幅要大于高质量比涡激振动振幅。曲宝旭[6]采用重叠网格法对具有弹性支撑不同自由度下输电导线的涡激振动进行了分析,结果表明:不同自由度对涡激振动横风向振动具有一定影响。
当前对圆柱涡激振动数值模拟主要是采用动网格技术,采用重叠网格法的相关报道相对较少。本文采用重叠网格技术建立网格,应用Newmark-β法求解结构振动方程,并且编制UDF(user defined functions),嵌入到Fluent中,通过宏命令DEFINE_ZONE_MOTION传递运动速度,以更新运动网格位置,对斜拉索结构涡激振动响应进行数值模拟,从而解决结构振动过程中可能产生的网格畸变和负体积问题,实现流固耦合计算。
1 理论基础
1.1 流体控制方程
不可压缩流体N-S方程和连续性方程分别为
(1)
(2)
式中:υ=μ/ρ为分子黏度,μ为动力黏度;fi为单位质量流体所受到的体积力(质量力);p为流体介质微元体上的压力;ρ表示流体密度;ui表示x、y、z方向的流体速度分量。
1.2 结构振动控制方程
以文献[7]中斜拉索实验模型为背景进行斜拉索涡激振动分析,斜拉索直径D设置为0.066 m。如图1所示,斜拉索可简化为两自由度质量-弹簧-阻尼系统,振动方程表示为
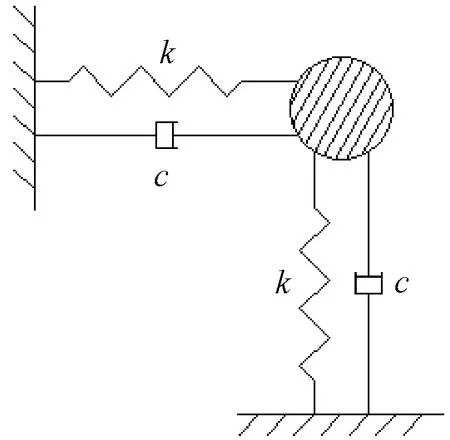
图1 两自由度质量-弹簧-阻尼体系
(3)
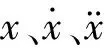
2 数值模型建立
在划分网格之前,要确定计算域的大小,合理的计算域大小可以使数值计算效率提高,也能保持计算结果的准确性。通常可以根据阻塞率的大小来确定计算域大小,在CFD模型中阻塞率一般控制在5%以内。二维流场计算域大小为24D×50D,其中D为圆柱的直径,如图2所示。定义圆柱截面形心所在位置为计算域坐标原点,设定重叠区域直径大小为3D,坐标原点到入口边界(INLET)的水平距离为15D,与出口边界(OUTLET)的水平距离为30D。上下两侧均为对称边界(SYMMETRY),其到坐标原点的垂直距离均为12D。拉索表面为无滑移壁面边界(NO-SLIPWALL)。在进行拉索涡激振动计算时,湍流模采用剪切应力输运模型(shear stress transition,SST)k-ω模型,湍流度设置为5%。该模型能较好地处理壁面附近的流动得到可靠的结果,适用于存在逆压梯度和流动分离的圆柱绕流场计算[8]。

图2 重叠网格划分
2.1 重叠网格划分及边界条件
重叠网格由背景网格和前景网格组成,也即流体计算域根据计算需要被划分为多个部件区域。首先在各区域单独创建网格,然后通过插值计算实现相邻计算域间的流场数据交换。与传统动网格计算相比,重叠网格在计算过程中,不会产生网格缠绕、畸变和负体积等问题,能始终保持计算网格的质量,从而保证计算结果的准确性。
采用CFD软件Fluent中的重叠网格(overset mesh)技术,进行圆柱体两自由度涡激振动响应计算。重叠网格技术的实施,包括两个主要步骤:1)在不同网格间建立通信关系;2)利用从步骤1中获得的信息,进行数值求解。
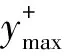
2.2 网格独立性与时间无关性检验
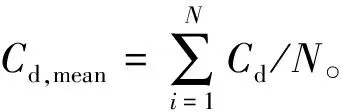
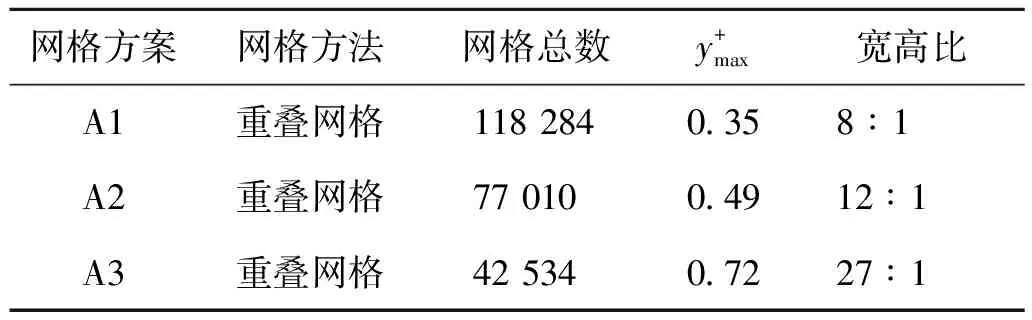
表1 网格方案详细参数设置
从图3(a)可以看出在不同网格方案设置下,拉索气动响应随着时间步的减小都能达到一个稳定的值,不同的是网格数量越大以及宽高比越小,也就是网格的整体质量越好(A1,A2网格),得到的阻力系数均值较A3网格方案得到的结果稍大。从图3(b)中可以看出,在不同网格方案下,采用A1和A2网格得到的St数在整体趋势上更加吻合,结果也比较接近。可以得出结论,采用A1和A2网格方案,得到St数与其他学者的结果比较一致,如表2所示。可以认为A2、A3网格方案已通过网格独立性以及时间无关性检验,继续对网格进行加密意义不大。综上所述,在考虑计算精确度和计算效率下,选择A2网格方案和时间步大小为0.002 s进行数值模拟。
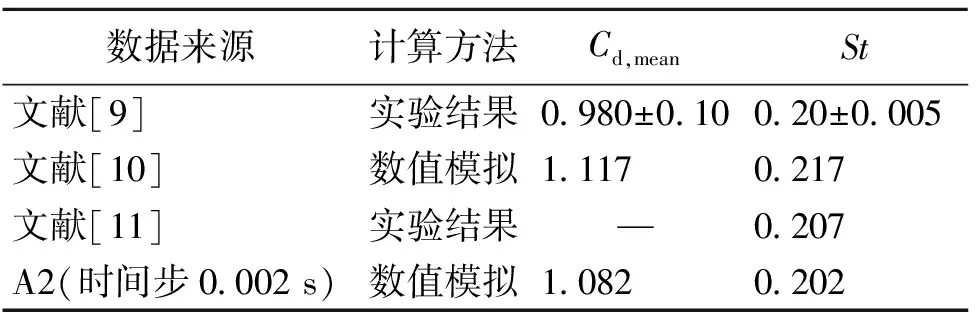
表2 Re=3 900时St数对比
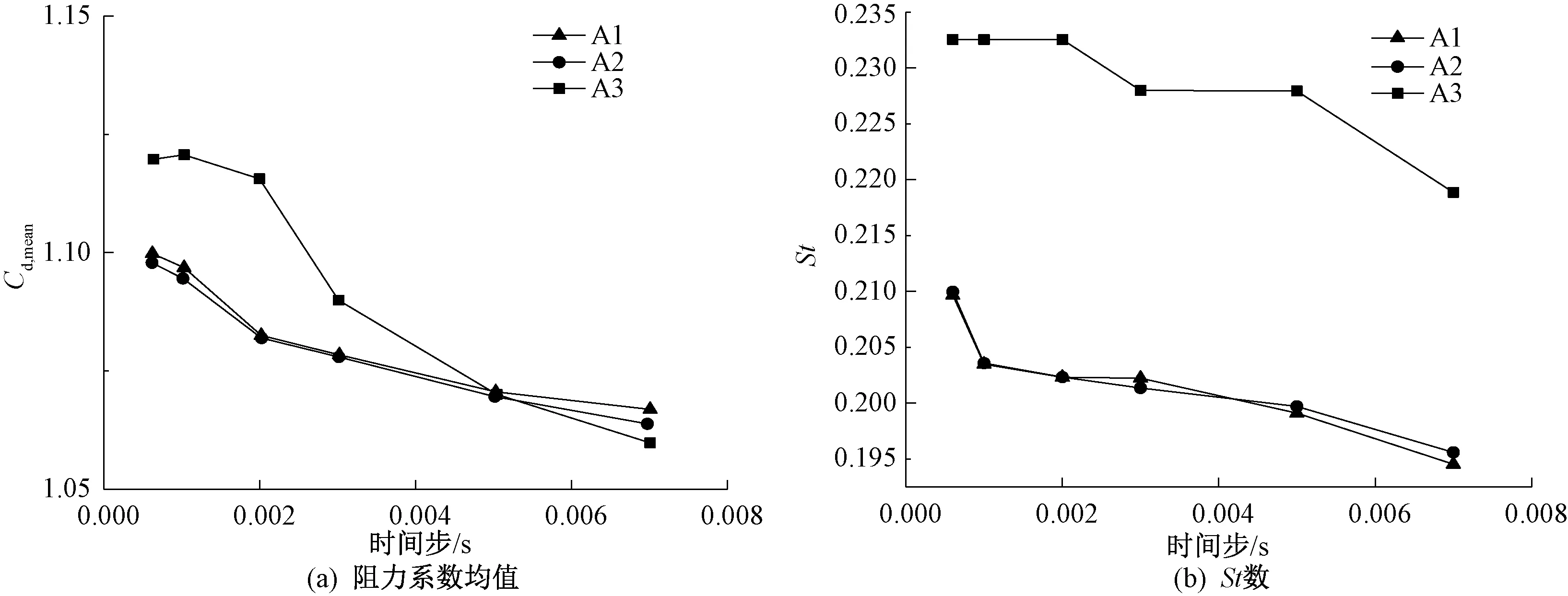
图3 阻力系数均值与St数随时间步大小的变化
3 斜拉索涡激振动响应特性分析
拉索在实际服役时,涡激振动起振的折减风速为Ur=U/(fn·D),通常小于10,所以选取的计算折减风速Ur范围为3.5~7.5,相应的雷诺数Re位于6 500~14 000之间。
3.1 St数及涡脱频率分析
图4(a)中可以看出,在折减风速Ur=3.5~4.64之间时,St数随折减风速变化呈线性下降的趋势;当Ur=4.727时,St=0.203;在Ur=4.64~4.94之间时,随着Ur的增大St呈倒“V”字形变化,即St数先突然增大,又急剧减小,此时对应拉索发生涡激振动的折减风速区间,可以推断这个区间内流场变化比较剧烈;当Ur>4.94时,St数又突然增大之后呈线性减小趋势。如图4(b)所示,随着折减风速增大,由于拉索发生了频率锁定现象(lock-in),所以在某一风速区间内拉索涡脱频率并没有线性增大;当涡脱频率约为3.494 Hz时,对应的折减风速为4.94;当Ur>4.59时,拉索涡脱频率没有随着折减风速的增大而增大,而是与在靠近拉索的一阶固有频率,所以,可以认为此处为锁定区间的起点;当Ur=5.04时,拉索涡脱频率与结构固有频率解锁,涡脱频率随折减风速的增加开始呈线性变化。从图4(b)中可以看出,拉索发生锁定的区间比较窄,也就说,拉索涡激振动对风速的变化非常敏感。
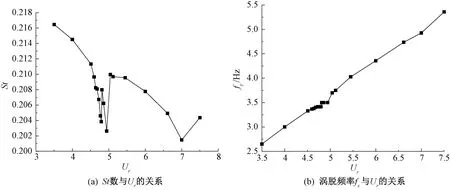
图4 不同折减风速下涡激振动St数与升力系数频率分析结果
3.2 振幅响应分析
图5给出了不同折减风速下拉索横风向无量纲位移时程曲线。从图5中可以看出,在高质量比下拉索在折减风速较低时,位移呈现微幅简谐振动,拉索的振动幅度也很小。随着折减风速的增加拉索振动幅度逐渐增大,并且出现了“拍振”现象。横向位移在折减风速Ur=4.67~4.94之间显著增加。
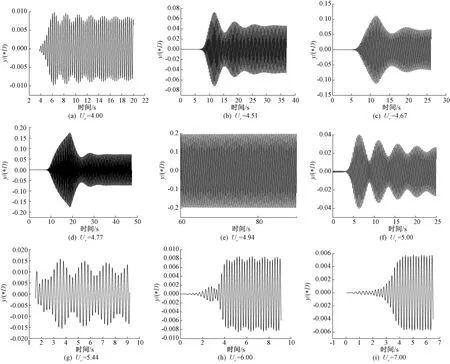
图5 典型折减风速下拉索横向振动位移时程曲线
如图6(a)所示,可以看出,在锁定区间拉索横风向振动频率接近拉索固有频率。在折减风速Ur=4.64~4.94之间时,漩涡脱落频率与拉索固有频率值非常接近,即拉索发生了“锁定”,拉索作大幅振动,并且在折减风速Ur=4.94时,拉索达到最大振幅0.20D左右(如图6(b)所示)。
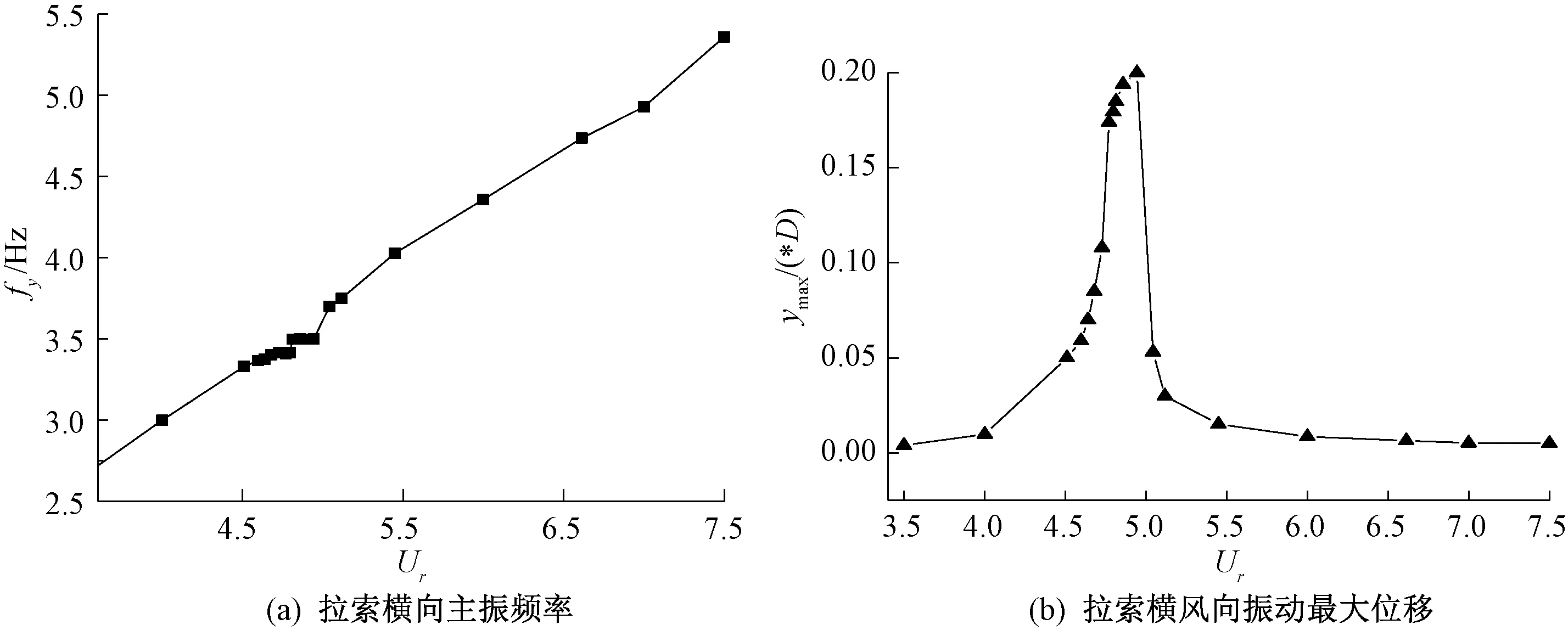
图6 不同折减风速下拉索横向主振频率与最大位移
3.3 拉索涡激振动轨迹分析
图7(a)~(g)给出了不同折减风速下拉索涡激振动的轨迹图。拉索涡激振动是以空气为介质进行计算,拉索的质量比m*=159.4,此时拉索应属于高质量比下涡激振动。高质量比情况下,涡激振动的运动轨迹形式更加复杂。在较低或者较高折减风速下,拉索振动轨迹主要呈椭圆形式,同时运动的方向和位置也在不断发生变化。在接近结构固有频率时,拉索在锁定区内也即流固耦合作用较强时,拉索运动轨迹大致呈“8”字形。低质量比圆柱涡激振动轨迹一般呈单一的“8”字形,高质量比结构涡激振动的运动形式更加丰富,在高质量比参数下拉索不再是单一的“8”字形运动,这与文献[6]的结论一致。
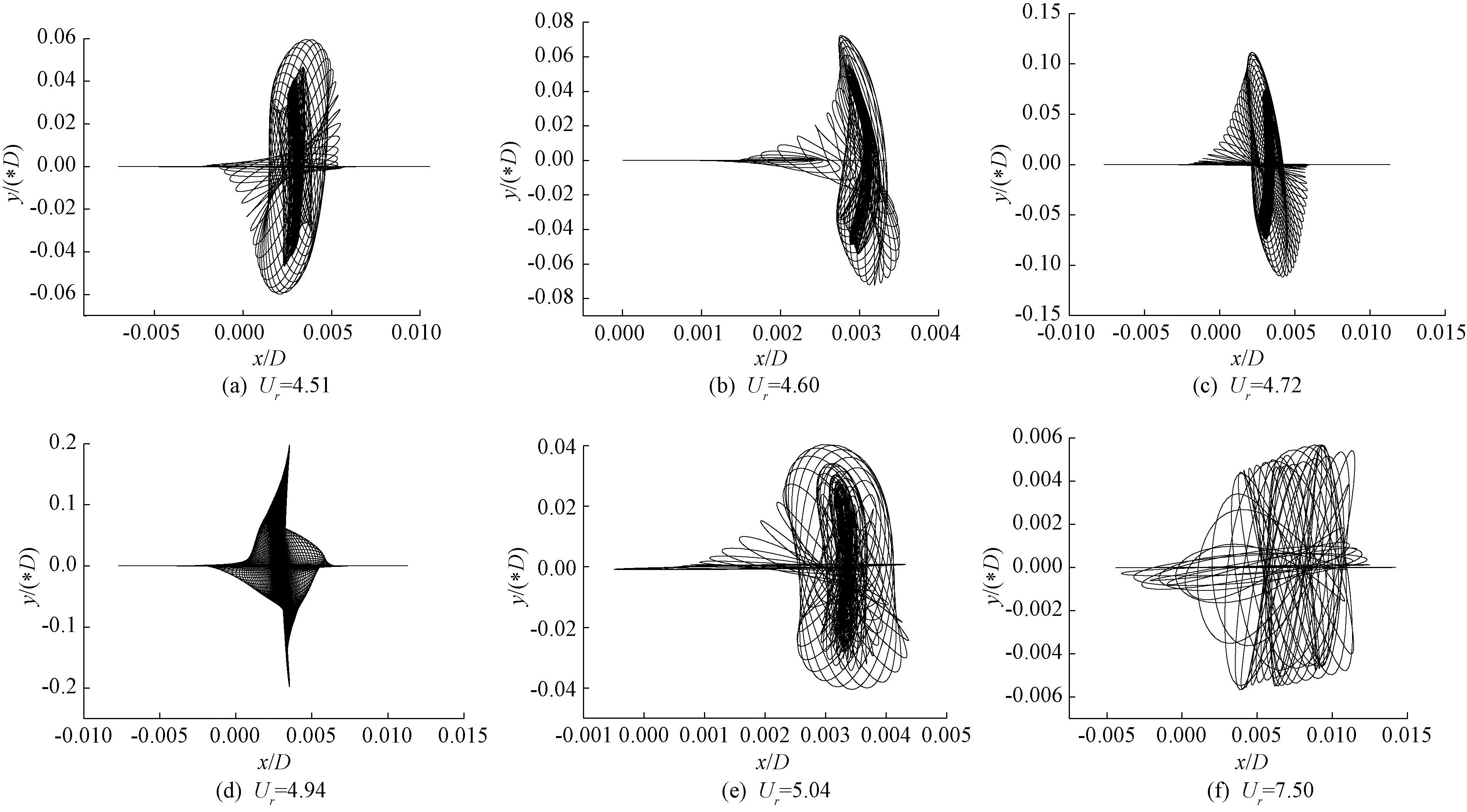
图7 拉索涡激振动质心运动轨迹
4 质量比对涡激振动影响分析
本节设定质量比m*=7.9作为低质量比情况,阻尼比保持ζ=0.546%不变(相对应的质量阻尼m*ζ=0.041 5),对拉索进行数值模拟。
从图8中可以看到,在质量比为159.4时,升阻力系数的均值是比较接近的,也就是说,在高质量比参数下,流场的变化并不是很强烈。对比不同质量比下拉索升阻力系数均值可以发现,低质量比参数下拉索升阻力系数均值变化的范围更广,横风向振动大小对升阻力大小有较大的影响,在结构振幅较大时,其升阻力也有一个非常显著的增大过程,但随着振幅的降低,其升阻力又重新降低,直到保持一个稳定的值。可以推断,低质量比参数下流场与结构之间的相互作用也更加显著。
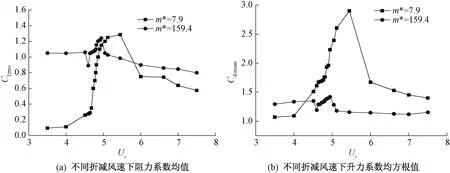
图8 不同折减风速及质量比下升阻力系数均值对比
如图9、10所示,相较于高质量比情况,拉索涡激振动的锁定区间也有所变大,由锁定区过渡到非锁定区较慢。当频率比为1时,拉索达到最大振幅为0.82D,为高质量比参数下最大振幅的4.1倍。在设置计算的有限工况内,涡激振动处于锁定区间时的锁定频率比在1.02左右,也就是说,锁定频率发生了小幅度的偏移。当频率比达2.318时,涡激振动振幅显著减小至0.05D,此时涡激振动已脱离锁定区间。
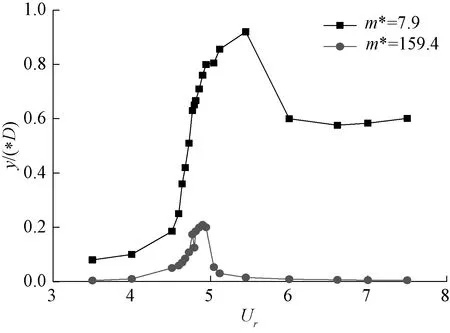
图9 不同折减风速下横风向最大位移变化
对比图8~10可以推断:质量比越小,结构发生涡激振动时锁定区间越宽,最大振幅也越大。随着质量比减小,发生锁定时的频率比也会有一定的偏移。
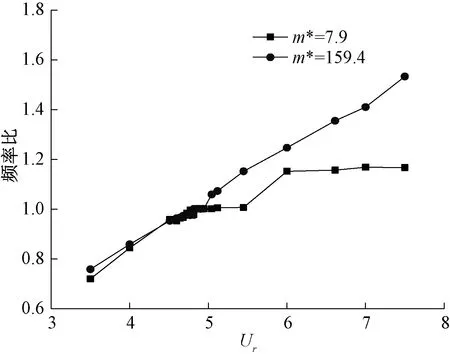
图10 不同折减风速下频率比变化
5 结论
通过对斜拉索进行涡激振动数值模拟,得出了4个结论。1)拉索发生涡激振动时,阻力系数均值首先降低至最小值,而后又显著增加到最大值。之后随着折减风速的继续增大,阻力系数均值呈不断减小趋势。升力系数均方根值随折减速度的增大(Ur=3.5~4.51)基本保持不变,之后升力系数突然降低,又在Ur=4.59~4.94之间保持显著增大的趋势,直至最大值,之后随折减风速的增加呈减小趋势;2)对于高质量比涡激振动,其振幅虽然较低,但由于振动产生的疲劳破坏要特别注意。只有在接近拉索一阶固有频率的范围内,拉索振幅显著增大,达到了0.2D,之后虽折减风速进一步增加,但振幅迅速减小,拉索振幅的变化对于折减风速的变化非常敏感;3)对拉索涡激振动的运动轨迹进行了详细的分析,拉索属于高质量比涡激振动,其运动轨迹更加丰富,只有在接近发生涡激振动的范围内,拉索大致呈“8”字形运动轨迹,这与低质量比圆柱的涡激振动轨迹有显著差异;4)质量比会对拉索涡激振动产生一定的影响,是影响涡激振动的重要因素。通过对低质量比涡激振动分析,可以得出结论:质量比越小,振动锁定区间越大,拉索在锁定区间内振幅也越大。
