基于虚拟电价的含电动汽车并网型微网经济调度策略

孙 宬，苏 适，赖煊平，朱 斌，周一凡，赵腾飞

（1.云南电网有限责任公司 电力科学研究院，昆明 650217；2.华北电力大学 电气与电子工程学院，北京 102206）

0 引言

随着全球能源枯竭及环境恶化问题的日益加剧以及清洁能源的不断发展［1］，微电网凭其灵活、清洁等优势得到了迅速发展，微网将分布式电源，储能装置和负荷紧密联系在一起，同时，新能源电动汽车凭借其节能和低排放的优势也得到了广泛的发展，2030 年全球预期的电动汽车（electric vehicle,EV）数量将达到2.2 亿辆［2］。但是由于分布式能源出力的波动性和大规模EV 无序接入微网，可能造成微网弃风弃光量大，负荷峰谷差加剧［3］，必定会严重威胁微电网的经济稳定运行。

EV具备其他常规负荷不具备的储能特性［4］，文献［5］建立了EV不同的充放电模型，并通过蒙特卡洛模拟法获得对应的充放电曲线，结果证明，有序管理EV的接入可有效实现平衡负荷和削峰填谷的作用，但是没有给出具体的优化方法。国内外的研究表明，在常规充电模式下，EV的充电过程一般不超过4 h。因此，EV可以中断负荷的方式参与电网的调控，又可作为分布式储能设备，在电网允许时，还可以向电网反向馈电（vehicle to grid，V2G），参与电网调控。

目前微网储能大多是按照集中式的模式进行配置和调度，少有学者综合考虑电价和微网功率供需情况。文献［6］采用分区需求侧管理的策略对混合微电网进行优化管理。文献［7］考虑不确定性因素，针对含风力和EV 充放电的虚拟电厂参与到电力市场中的问题，提出了一种混合储能虚拟电厂参与电力市场的调度策略。

本文针对可再生能源和EV 接入微网的问题，提出一种考虑电价激励的含电动汽车并网型微网经济调度策略，以提高光伏利用率和提高微网运行的经济性为目标，考虑可再生能源出力和等效负荷水平，构建以动态虚拟花费最小为目标的优化模型。采用非线性粒子群算法对模型进行优化求解；通过算例验证了本文方法的有效性。

1 含可再生能源和电动汽车微网的调度优先级

本文研究的并网型微网主要考虑光伏，储能装置，EV，蓄电池（BAT）。为保证最大化消纳光伏，光伏等可再生新能源在微网调度过程中有着较高的优先级。在考虑峰谷时段情况下，结合可再生能源和负荷的情况分析微网其他各部分的调度优先级。

（1）可再生能源出力充足

当处于峰时段，应先减小从大电网的购电量，并在微网内部应优先满足微网内部的EV充电需求，一定程度上向大电网反送电，获取调峰辅助收益，最后考虑储能装置；当处于平时段，向大电网反送电的收益较小，应先满足EV和BAT的充电需求；当处于谷时段，优先利用低电价对BAT和EV进行充电。

（2）可再生能源出力不足

当处于峰时段，从电网购电成本较高，而电动汽车放电收益较高，应减少购电量并应优先考虑EV和储能装置的放电；当处于平时段和谷时段，此时EV 放电收益较低且BAT 的充电成本也不高，所以EV放电的优先级最低；在谷时段时，EV充电优先级最高，BAT充电优先级次之。

2 含电动汽车并网型微网经济调度模型

2.1 动态虚拟电价模型

假设第i时段内共接入N辆EV，第k辆1 ≤k≤N接入微网内部的EV，等效负荷为

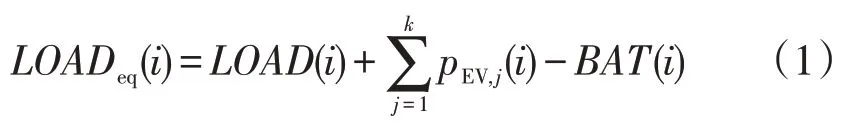
式中:LOAD(i)、、BAT(i)分别为第i个时段基本负荷、第k辆EV 接入时的EV 充电功率的总和、蓄电池出力。等效负荷考虑了同时段接入的其他EV 的影响，可以有效避免在电价低谷时造成新的用电高峰问题。

对于EV 接入、离开时间及初始荷电量的不确定性本文采用文献［8］的统计结果，即接入、离开时间分布满足正态分布N1=（9，0.52）、N2=（19，1.52），并假设各有一半电动汽车满足上述正态分布；初始荷电状态（state of charge，SOC）电量状态采用文献［9］的结果，满足正态分布N（0.6，0.22）分布。

光伏24 h 出力及第i个时段的出力分别为

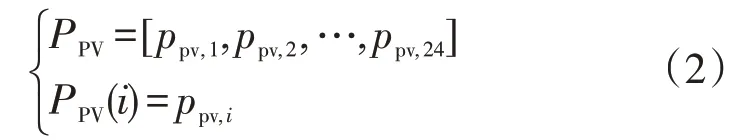
对于第i个时段，第k辆接入微网的EV 对应的供需不平衡率与前k-1 辆EV 的充放电功率有关。定义第k辆EV接入时对应的供需不平衡率为

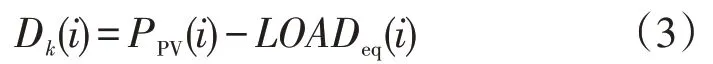
由式（3）可知，随着同时段接入EV 数量的增多，Dk(i)会相应减小。

Dk(i)可以反映光伏出力的充裕程度，对不同Dk(i)和峰谷电价情况确定微网各部分的调度优先级，如表1所示。

表1 不同Dk(i)和峰谷电价对应的优先级Table 1 Priorities corresponding to different Dk(i)

各部分在i时段对应的动态虚拟电价pGrid(i)、，其中分别为在第i时段接入微网的第k辆EV和从大电网购电对应的虚拟电价；pBAT(i)为储能i时段对应的虚拟电价。如式（4）所示

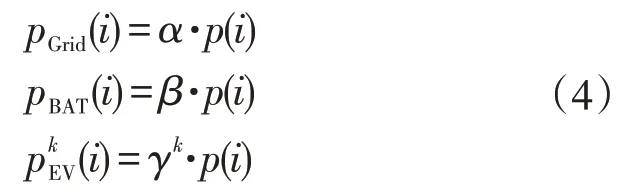
式中:α、β、γk分别为虚拟电价系数，与该时段的和峰谷电价p(i)对应的优先级有关。

2.2 动态虚拟电价作用机制

虚拟电价的设定原则是根据微网内部负荷和光伏出力情况并结合实际电价水平实现微网的稳定经济运行并提高光伏消纳量。以某园区光伏和基本负荷情况为例，微网光伏和负荷差值如图1所示，实际电价如表2所示。

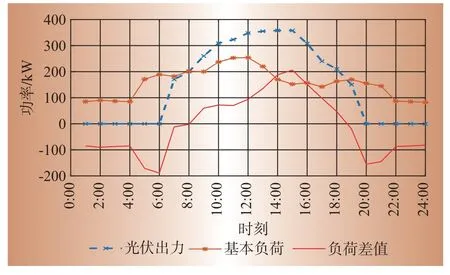
图1 微网光伏和负荷差值Fig.1 Microgrid PV and load difference

表2 实际电价Table 2 Actual electricity prices元/kWh

根据实际电价水平和Dk对优先级的影响，对应的动态虚拟电价如图2所示。

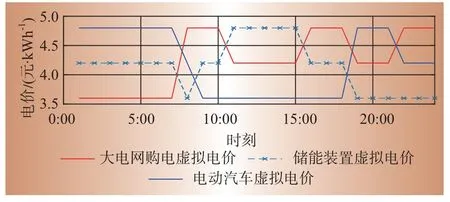
图2 微网各部分对应的虚拟电价Fig.2 Virtual electricity price corresponding to each part of micro grid

以第15 个时段为例，由图1 知，该时段光伏出力充足，满足负荷后的余量较多。此时Dk大于0并且处于峰值电价，根据表1所示的调度优先级，应优先给EV进行充电，向大电网反送电此时收益最高，而储能装置优先级最低。由图2 看出在第15 时段的动态虚拟电价能够很好的实现引导控制效果。

2.3 微网调度模型

2.3.1 目标函数

以促进新能源消纳和提高微网运行的经济性为目的，在保证EV用户需求的情况下，将一天划分为24个时段，并基于动态虚拟电价构建动态虚拟花费最小的目标函数，将各时段的EV充放电功率和储能装置的出力视为优化变量。满足EV用户的充放电需求以及结束充电时的荷电状态（state of change,SOC）期望值的同时，保证微网的经济运行。目标函数为

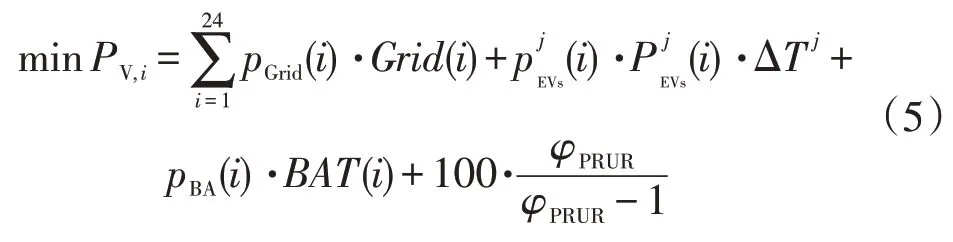
式中:pGrid(i)、Grid(i)分别为第i时段从大电网购电的虚拟电价和交互功率；pBA(i)、BAT(i)分别为第i时段蓄电池所对应的虚拟电价和充放电功率分别为第i个时段第j辆EV的虚拟电价和充放电功率；ΔTj为第j辆EV的调度时间；φPRUR为光伏利用率。

其中光伏利用率为

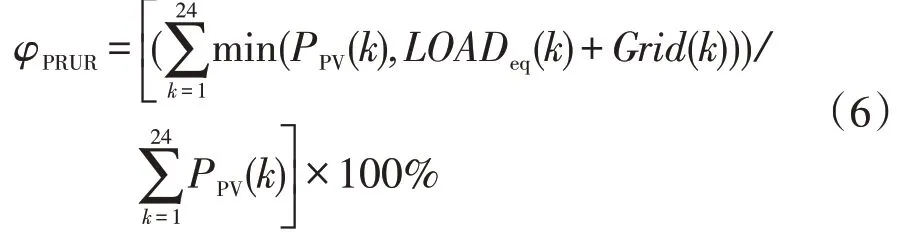
2.3.2 约束条件

（1）微网功率平衡约束

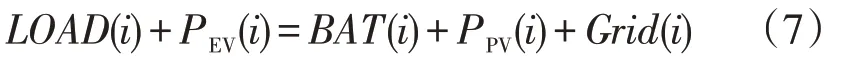
式中:PEV(i)为第i时段所有EV的充放电功率总和。

（2）蓄电池出力约束及爬坡约束

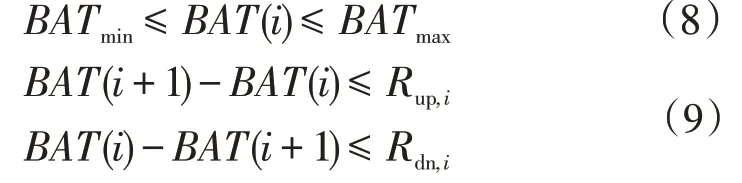
式中:BATmin、BATmax分别为蓄电池的最小、最大出力；Rup,i、Rdn,i分别为蓄电池的爬坡上、下限。

（3）EV电池储存电量约束

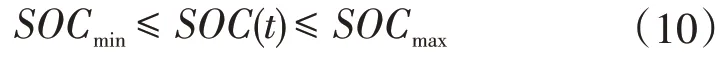
式中:SOC(t)为第t个时段的电池SOC状态；SOCmin和SOCmax分别为电池电量的最小、最大值。

SOC(i)和充放电功率有关，具体关系为

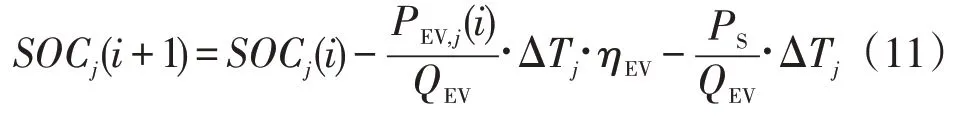
式中:SOCj(i)为第j辆EV 在第i时刻的荷电状态；QEV为电动汽车电池的容量；ηEV为充放电效率；PS为自放电功率。

（4）单个EV充放电功率约束

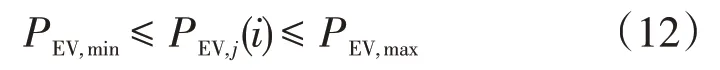
式中:PEV,min和PEV,max分别为EV 每时段的功率下限和上限。本文同时考虑EV 的充电和放电，放电时PEV,j(i)<0，反之，PEV,j(i)>0。

（5）EV接入数量约束

为避免对微网造成新的调峰压力，接入数量约束为

式中:NEV,max为同时段接入EV的最大数量。

（6）蓄电池、EV的充放电次数约束

频繁的充放电动作会严重影响其使用寿命，设置蓄电池、EV在一个调度周期24h内分别最多切换5次、3次。

（7）与大电网交互功率约束

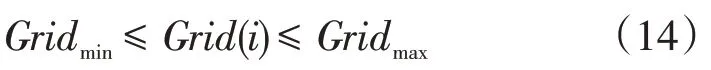
式中:Gridmin、Gridmax分别为与大电网交互功率的下限和上限。

3 算法与流程

3.1 考虑粒子历史最劣解的非线性粒子群算法

传统的粒子群算法从随机解出发，通过迭代寻找最优解。个体粒子在迭代过程中的位置和速度更新为

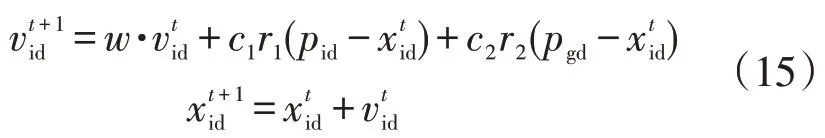
式中:w为惯性权重系数；分别为第t次迭代的第i个粒子的速度和位置；pid为第i个粒子迭代过程中的个体最优值；pgd为所有粒子的全局最优值；c1和c2分别为学习因子，也叫加速常数；r1和r2分别为0到1的均匀随机数。

本文提出了一种考虑粒子历史最劣解的非线性粒子群算法，在迭代过程中标记出粒子自身历史最劣值和群体历史最劣值，并选取部分粒子在迭代过程中追踪这2个极值进行搜寻。

对于追踪个体最劣解piworst、全局最劣解pgworst的粒子在迭代时的位置和速度更新公式为

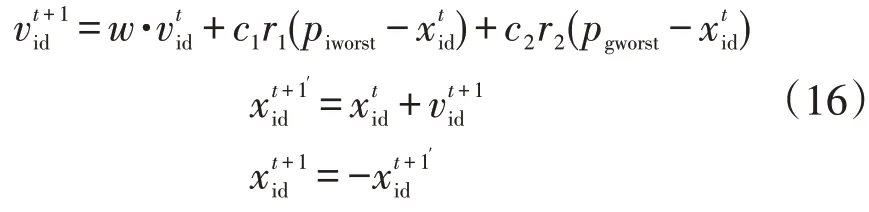
对于2类粒子位置的更新方式如图3所示。

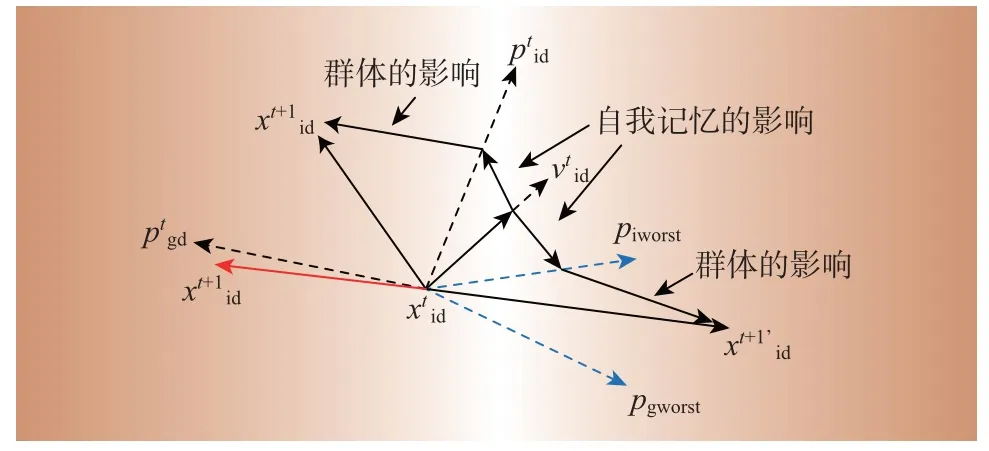
图3 粒子位置更新Fig.3 Particle position update

通过调整惯性权重系数ω可以大大提高算法的性能，提高寻优能力。本文针对ω的特点，在迭代过程中对其进行非线性化处理，如式（17）在迭代前期减小斜率上凸化，在迭代后期的减小斜率下凹化，如图4所示。即

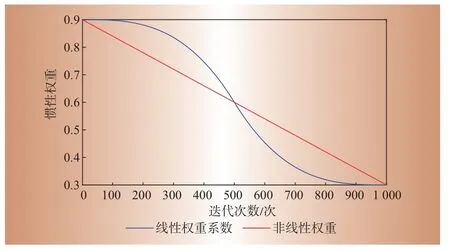
图4 非线性惯性权重系数Fig.4 Non⁃linear inertial weight coefficients

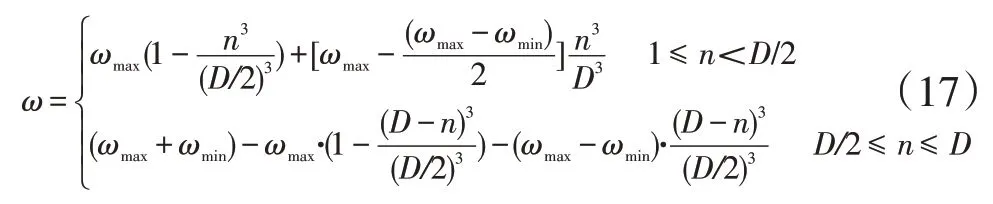
式中:ωmax、ωmin分别为惯性权重系数的最大值、最小值；D为最大迭代次数；n为当前迭代次数。

3.2 算法步骤

本文采用的考虑粒子历史最劣解的非线性粒子群算法步骤如下:

（1）初始化粒子群，其中包含种群规模和各粒子的初始位置和速度；

（2）计算每个粒子的适应度，记当前粒子个体和种群的最优、最劣适应度；

（3）将粒子进行分类，在总体粒子中随机选取30%的粒子根据式（15）更新位置和速度；剩余粒子根据式（16）更新位置和速度；

（4）重新计算更新后的粒子适应度，并更新当前粒子个体和种群的最优、最劣适应度；

（5）判断是否满足搜索精度或达到设定的最大迭代次数。若是，则停止迭代并输出结果；若否，转到第（3）步，直至满足条件。

4 算例分析

以含光储和电动汽车的某园区微网为例，设该微网系统中的EV可接入的上限值为50辆，EV的电池容量为60 kWh，充放电功率限值均为8 kW，充放电效率为0.95，自放电功率为5.2%，SOC的上下限分别为0.95、0.20。

光伏出力和园区微网基本负荷情况及二者功率缺额，如图1 所示。设置算法迭代次数为1 000，粒子数目50，权重系数ω最大、最小值分别为0.9、0.3，学习因子c1、c2均设置为2。

分别采用传统峰谷电价、实时电价和动态虚拟电价对微网进行优化调度得到蓄电池出力、微网与电网交互功率、微网等效负荷水平。结果如图5 所示。

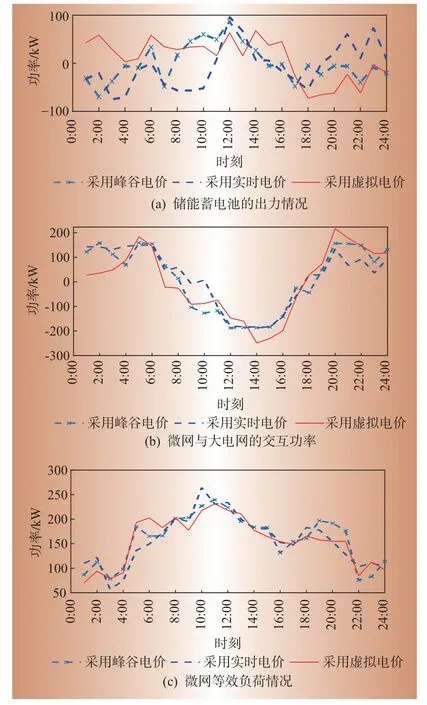
图5 仿真结果Fig.5 The simulation results

图5（a）所示，在17:00以后蓄电池由正变为负，由放电状态转变为充电状态；结合图5中各结果，在14:00 光伏充足，负荷水平有所下降，但此时电价仍处于峰段，为提高微网整体的经济性，向大电网的倒送功率有所增加以获取峰段收益。

在光伏充足且实际电价较高时，在虚拟电价的引导下，微网向电网的倒送功率较其他2 种电价大。这是由于此时储能装置充电的优先级低于交互功率，此时向电网倒送功率能发挥光伏的利益最大化。

采用不同电价机制下的优化结果如表3所示。

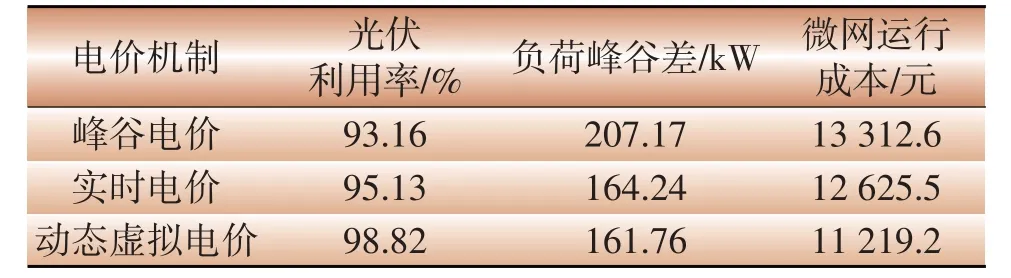
表3 不同电价机制下的优化结果Table 3 Optimization results under different pricing mechanisms

结合上述仿真数据可见，采用动态虚拟电价时光伏的利用率为98.82%，对比相同情况下峰谷电价和实时电价分别提高了5.66%、3.69%；负荷峰谷差分别减小了45.41 kW、2.48 kW；微网的运行成本分别降低了2 093.4元、1 406.3元。从优化结果可见本文提出的基于动态虚拟电价机制能够提高微网的光伏消纳能力并且能够提高微网运行的经济性，起到一定的削峰填谷能力，同时也验证了动态虚拟电价的正确性和有效性，并且能够保证微网的安全、稳定、经济运行。

下面从迭代的收敛性和收敛速度角度比较本文提出的考虑粒子历史最劣解的非线性粒子群算法和传统粒子群算法的性能。以仿真实例结果，二者优化的计算时间分别为14.563 572 s和20.182 356 s，本文提出的算法较传统算法节省了5.62 s，目标函数在迭代过程中的变化，如图6所示。

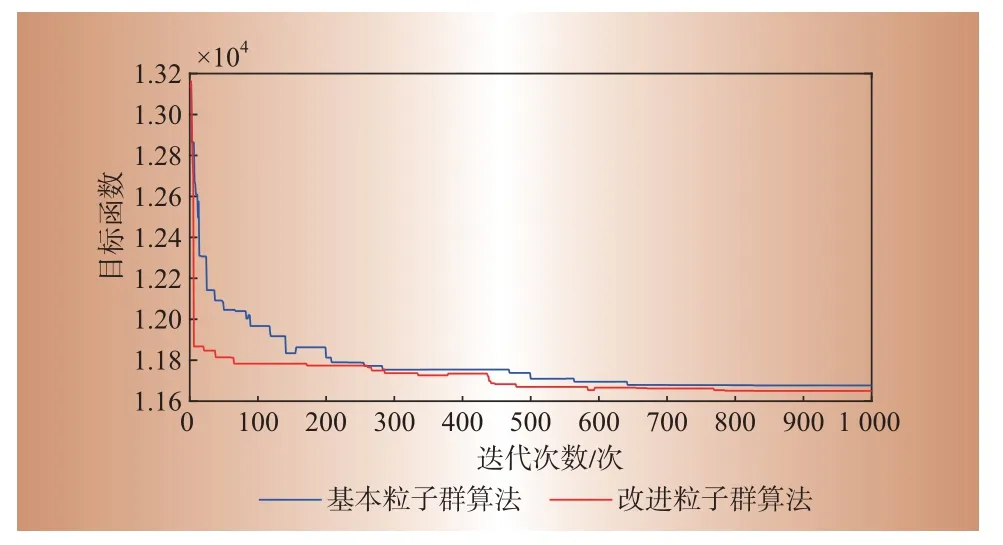
图6 2种粒子群算法的迭代对比Fig.6 Iterative comparison of the two particle swarm optimization algorithms

随着迭代次数的增加，标准粒子群算法和本文提出的非线性粒子群算法均能向着最优方向搜寻，可以看出非线性粒子群算法在迭代过程中能够较快地搜寻到最优值，效果更好。这是因为非线性粒子群算法充分利用了迭代过程中的粒子的历史信息，在迭代过程中增加了粒子位置和速度的多样性，符合计算应用的要求。

5 结束语

本文以包含光伏，储能装置及电动汽车的园区微网为研究对象，提出了一种综合考虑峰谷电价和光伏出力及等效负荷不平衡率的动态虚拟电价模型实现微网的经济调度；在仿真实例下，建立动态虚拟花费最小的目标函数并考虑相关约束条件，在动态虚拟电价的引导下确定微网各部分的出力情况，尽可能实现系统的安全性、稳定性和经济性等量化指标的优化。