电动汽车充换储一体化电站的优化调度策略及应用

叶 婷，邓 星，黄 堃，梁加本，张智俊

（1.国网江苏省电力有限公司 南京供电分公司，南京 210019；2.国电南瑞科技股份有限公司，南京 211100；3.南京邮电大学，南京 210023）

0 引言

伴随新时代“能源革命”的推进，以电动汽车为代表的新能源为电网提供了源源不断的能源供应。与此同时，电动汽车充放电的无序化、随机化也给电网的运行管理带来了巨大的挑战。为此，如何对电动汽车进行精准预测并进行优化管理至关重要。通过对园区内电动汽车充换储一体化电站、中断负荷以及分布式发电源（distributed generator，DG）等重要元素进行集中监控管理，建立“区域协控虚拟电厂”典型模型，研究区域可调资源聚合技术，可下发实际调控指令，充分发挥电动汽车充换储一体化电站和分布式电源的灵活调节能力，在兼顾个体利益的前提下，实现区域整体利益最大化。

文献［1］针对电动汽车充电行为不确定性问题，建立了基于出行链理论的电动汽车出行及电池电量变化模型，提出了引入马尔科夫决策过程的电动汽车用户充电行为分析方法。文献［2］提出了基于聚类分析的电动汽车充电负荷预测方法，在分析常规充电负荷影响因素并初步建立概率分布模型的基础上，对每段行程的行驶里程和行驶时间构成的二维出行特征数据进行聚类分析。文献［3］以出行时间和行驶里程确定且充电时间不受分时电价影响的电动公交车、出租车和公务车为研究对象，提出了一种根据某市现行峰平谷电价政策并综合充电起始和结束时间所处的峰平谷阶段动态修正充电目标的EV充电负荷预测方法。上述方法都能将不同层面的不确定因素考虑进电动汽车的用电预测过程中，在一定程度上改进了预测性能。但这些现有方法也存在不足:都只考虑了出行习惯，忽略了要综合气象数据、预报信息，对影响电动汽车用电需求的因素进行深入分析，从多个方面一起考虑，进而提升电动汽车的用电功率预测的准确性。

为了促进多能源互补及能源低碳化，文献［4］提出了计及电转气协同的含碳捕集与垃圾焚烧虚拟电厂优化调度模型。针对VPP 内部风光资源的不确定性给其参与调峰市场带来影响的问题，一些文献对以VPP 为主体参与调峰市场开展研究。文献［5］采取VPP 同时参与直接电力交易市场与调峰市场的运营模式，计及风光出力不确定性的影响，提出基于条件风险价值理论的VPP 日前优化运行模型，并利用Shapley值法对各成员联合运行后取得的期望成本进行合理分配。但经分析可知，文献［4］、文献［5］着重解决风机、光伏等可再生电源参与虚拟电厂优化调度带来的不确定性问题，对解决大量可再生能源的并网消纳问题提供了很多有效方法。但这些文献也存在不足:在虚拟电厂优化过程中，较少考虑电动汽车和新能源同时进行优化调度，且少有算法能快速有效地求解出调度策略，实现能量互补和削峰填谷。

本文研究的虚拟电厂的运营模式是指通过建立虚拟电厂控制模型，挖掘包括充换储一体化电站、可中断负荷和分布式电源的时空互补特性，并对其运行方式进行最优化控制，从而为电网提供辅助支撑服务。首先，综合气象数据、预报信息，对影响电动汽车用电需求的因素进行深入分析，实现对电动汽车的用电功率预测；其次，基于提出的改进粒子群算法，实现虚拟电厂的整体经济效益最大化，通过最优化虚拟电厂各组成单元的运行方式，实现发用电互补，从而为电网的削峰填谷提供一定的支撑能力。

1 电动汽车负荷预测

电动汽车行驶活动具有很强的时空随机性，为描述其动态行驶过程，引入了出行链的概念，通过记录用户日常出行的首次出行地点和行程结束地点，直至这两个地点重合，形成一个完整的“链条”［6—9］。用户的日常出行特征可以用出行链完整地反映出来，基于所提出的出行链对其充电需求进行分析，从而为其用电功率预测提供保障［8—9］。为了更好地了解出行链的概念，用虚线表示用户出行的行驶过程，实线表示用户出行的停车过程，实心点表示出行链的起点与终点，如图1所示。

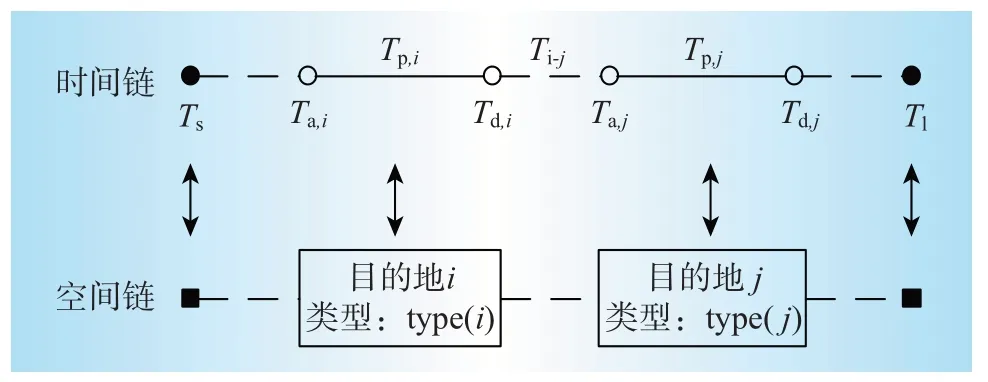
图1 出行链示意图Fig.1 Schematic diagram of travel chain

图1 中，Ta,i、Td,i分别为到达、离开目的地i的时刻；Ta,j、Td,j分别为到达、离开目的地j的时刻；Tp,i为用户在目的地i的停车时间；Ts、Tl分别为用户出行链的起点、终点时刻；Ti-j为用户从目的地i行驶至目的地j的花费时长。

1.1 出行链的时间分布

时间特征量在这次出行活动中满足如下公式

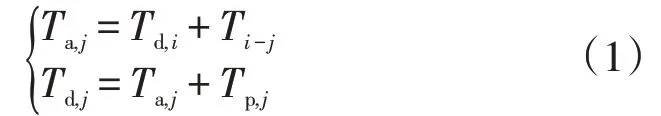
式中:Ta,i、Td,i分别为到达、离开目的地i的时刻；Ta,j、Td,j分别为到达、离开目的地j的时刻；Tp,i为用户在目的地i的停车时间；Ti-j为用户从目的地i行驶至目的地j的花费时长。

（1）首次出行时间概率分布

由文献［9］可知，用户每日出行链起点的时间概率密度f(t)服从正态分布，记作，其中，μs是出行链起点时间的均值，是出行链起点时间的方差，具体可以通过下式描述

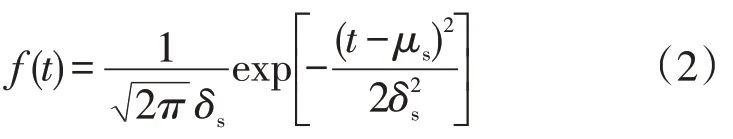
（2）电池荷电状态分布和充电时长

设电动汽车在当前时刻T0的荷电状态为SOC(T0)，则它在T时刻的荷电状态SOC(T)，可以通过下式计算

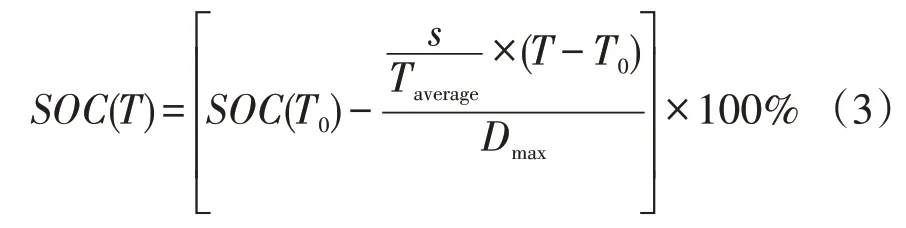
式中:s为T0时刻到T时刻的行使距离；Taverage为日行驶时间的平均值；Dmax为最大行驶距离。

一辆电动汽车的充电时长主要取决于其充电时长、其充电接口功率Pc、和其电池的荷电状态，表示如下

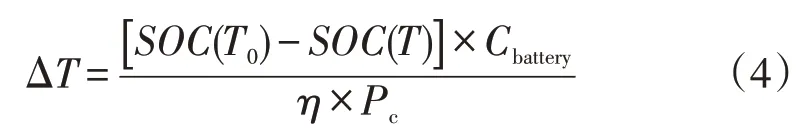
式中:Cbattery为电池容量；η为充电机的充电效率。

1.2 出行链的空间分布和充电时间的概率密度

由文献［10］可知，用户的出行链服从马尔科夫链，即用户下一时刻的出行地点只跟当前时刻的出行地点有关，并将用户出行链中的每个地点表示为状态，通过状态之间的转换表示其出行地点的变化。

记用户车辆的状态集为:{E1,E2,…,En}，用户车辆从状态Ei转为状态Ej的状态转移概率用pi-j表示，则pi-j满足条件如下

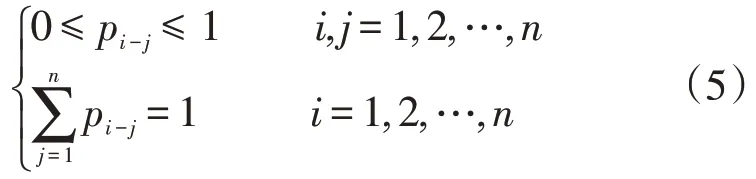
本文中，当前时刻用户的行驶地点集合被构建为:{办公区W，住宅区H，娱乐区E}，则用户车辆从任一地点i行驶到下一个目的地j的状态转移概率Pi-j可以表示为

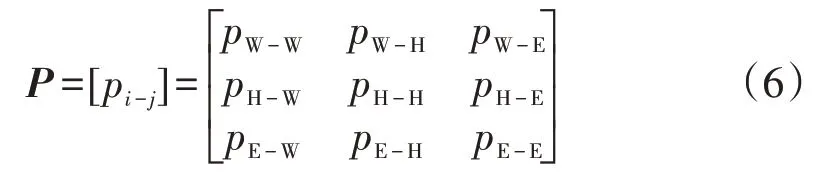
式中:fc(t)为起始充电时间的概率密度，则fc(t)基本服从分段正态分布［1］如下

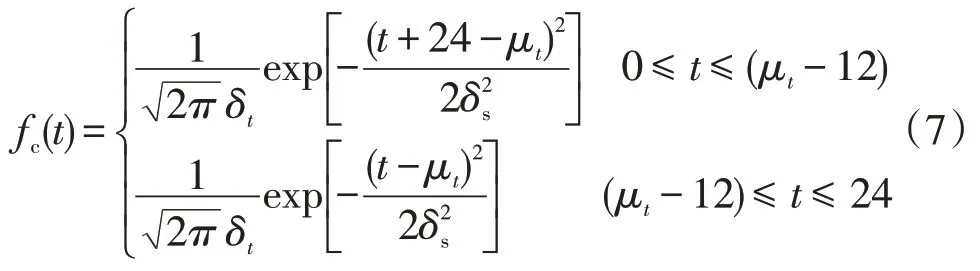
式中:μt、δt分别为充电起始时间的期望、方差。

1.3 电动汽车的负荷预测

基于上述对电动汽车时空特性的分析与建模，本文采用蒙特卡洛算法并综合不同功能区的停车需求模型，得到其负荷曲线，从而实现电动汽车的负荷预测。

我们以第n辆电动汽车到达目的地i的情况为例进行分析:在电动汽车到达目的地的时刻Ti,s时汽车到达目的地并进行时长为ΔT的充电工作。由于起始充电时间与充电时长是相互独立的参数，所以根据已知的电动汽车所需要的充电时长的概率密度，可以结合已知的不同充电方式下电动汽车起始充电时间的概率密度函数得到2 者的联合概率分布函数Fs,c服从以下条件

式中:Fs为采用快速充电方式下起始时刻的概率密度函数；Fc为采用常规充电方式下起始时刻的概率密度。

进一步可以求得，在T时段，电动汽车充电的概率为

在T时段，令Eij(T)×Fck为采用常规充电方式的电动汽车数量，Eij(T)×Ffk为采用快速充电方式的电动汽车数量。则采用常规、快速充电方式的负荷Qi-j,c(T)、Qi-j,f(T)可计算如下

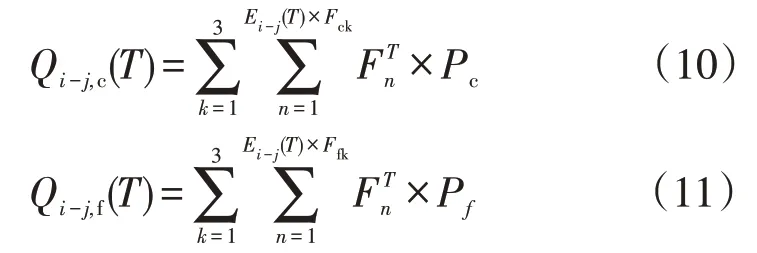
式中:Pc为常规充电功率；Pf为快速充电功率。

基于式（10）、式（11），在T时段，电动汽车总负荷Qi可以由下式进行计算

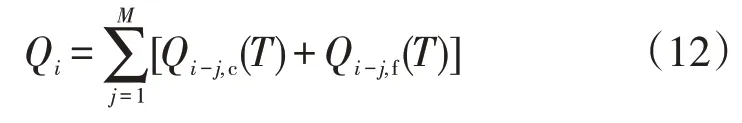
式中:Qi-j,c(T)为常规充电方式下电动汽车从地点i行驶至地点j对应的充电负荷；Qi-j,f(T)为快速充电方式下电动汽车从地点i行驶至地点j对应的充电负荷。

基于上述各时段电动汽车的负荷预测，结合电动汽车充换储一体化电站的储能容量，即可获得电动汽车充换储一体化电站可调度最大容量。

2 基于电动汽车预测的源荷储协同调度策略

基于园区内电动汽车充换储一体化电站、中断负荷以及分布式发电等重要可调控单元，建立“区域协控虚拟电厂”典型优化模型。

2.1 优化目标函数

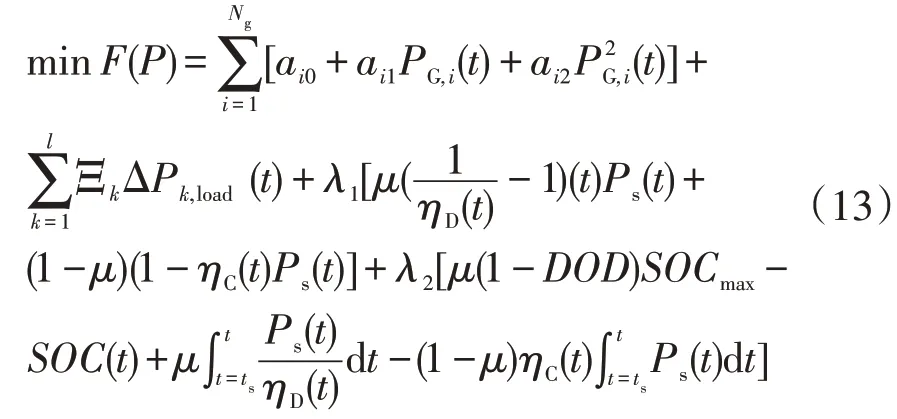
式中:F(P)为目标函数，即整个虚拟电厂的运行成本；Ng为分布式电源个数；ai0、ai1和ai2为成本系数；PG,i(t)为第i个分布式单元在t时刻的出力；ΔPk,load(t)为第k个可中断负荷；Ξk为第k个可中断负荷赔偿成本；λ2为电池的损耗成本；ts为运行初始时刻；ηc(t)、ηD(t)分别为电动汽车充换储一体化电站在t时刻的充、放电效率，放电时μ=1，充电时μ=0；DOD为放电深度；SOC(t)为电动汽车充换储一体化电站在t时刻的荷电状态；SOCmax为电动汽车充换储一体化电站最高荷电状态；Ps(t)为电动汽车充换储一体化电站在t时刻的调度功率。

（1）约束条件

功率平衡约束

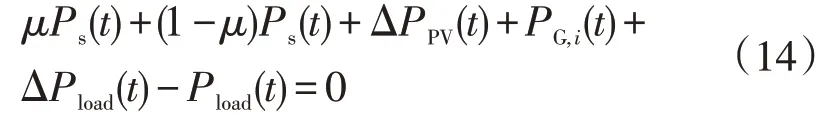
式中:ΔPload(t)为可中断负荷；Pload(t)为负荷在t时刻的预测功率；PPV(t)为负荷在t时刻的光伏发电功率，μ代表放电状态，放电时μ=1，充电时μ=0。

发电机组出力约束

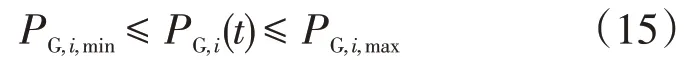
式中:PG,i,min为发电机组出力的最小值；PG,i,max为发电机组出力的最大值；PG,i为发电机组出功。

可中断负荷出力约束

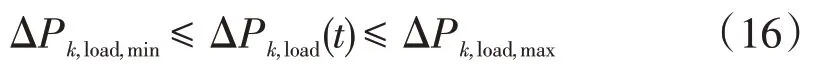
式中:ΔPk,load,max、ΔPk,load,min分别为可中断负荷的最大值、最小值；ΔPk,load(t)为t时刻的可中断负荷出力。

储能充放电约束

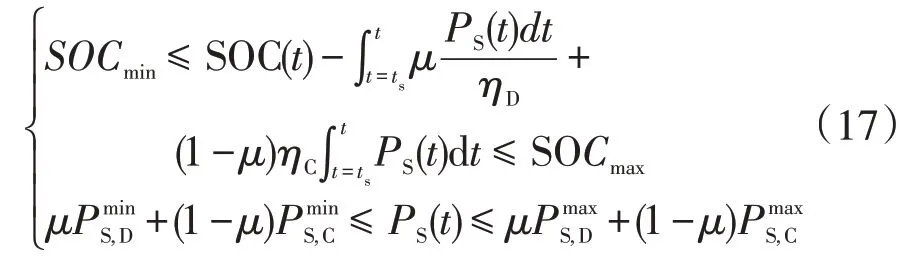
爬坡率约束

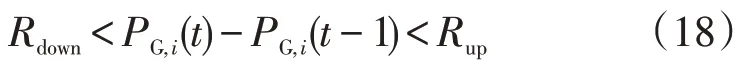
式中:Rdown为爬坡率的下限；Rup为爬坡率的上限。

2.2 优化目标函数求解

对于模型的求解，采用改进的粒子群的优化方法。

在园区虚拟电厂经济调度优化模型中，关于等式约束的处理，采用动态处理的方法，使得每个粒子在寻优的过程中可以始终满足等式约束。具体过程如下［11—12］:

①优先设置索引时间段t以及粒子群算法寻优过程初始化系数（粗调系数Jcoarse、细调系数Jfine），其具体值如下

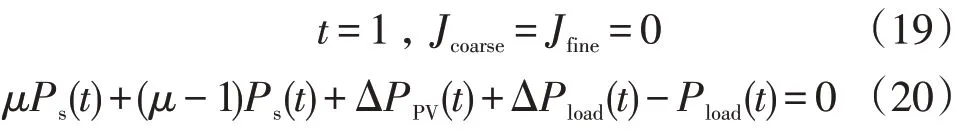
式中:μ为充放电状态，放电时μ=1，充电时μ=0；Ps(t)为电动汽车充换储一体化电站在时刻的调度功率；ΔPPV(t)为t时刻的光伏出功变化量；ΔPload(t)为t时刻的负荷需求变化量；Pload(t)为t时刻负荷初始需求量。

总功率差ΔP可以由式（20）获得，如果ΔP满足在允许的总的功率差ε的范围，转至步骤⑤，否则，进行步骤②。

通过式（2）可以获得发电机组在每个时间段内的发电需求功率，并基此进行调整，检查是否发电机组，其中分别是第i个发电机组的功率额定上、下限。在有Ns个发电源的系统中，调整后第i个电源的出功PG,i(t)为

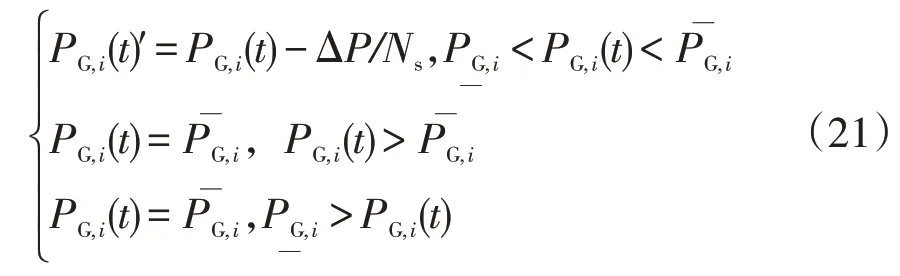
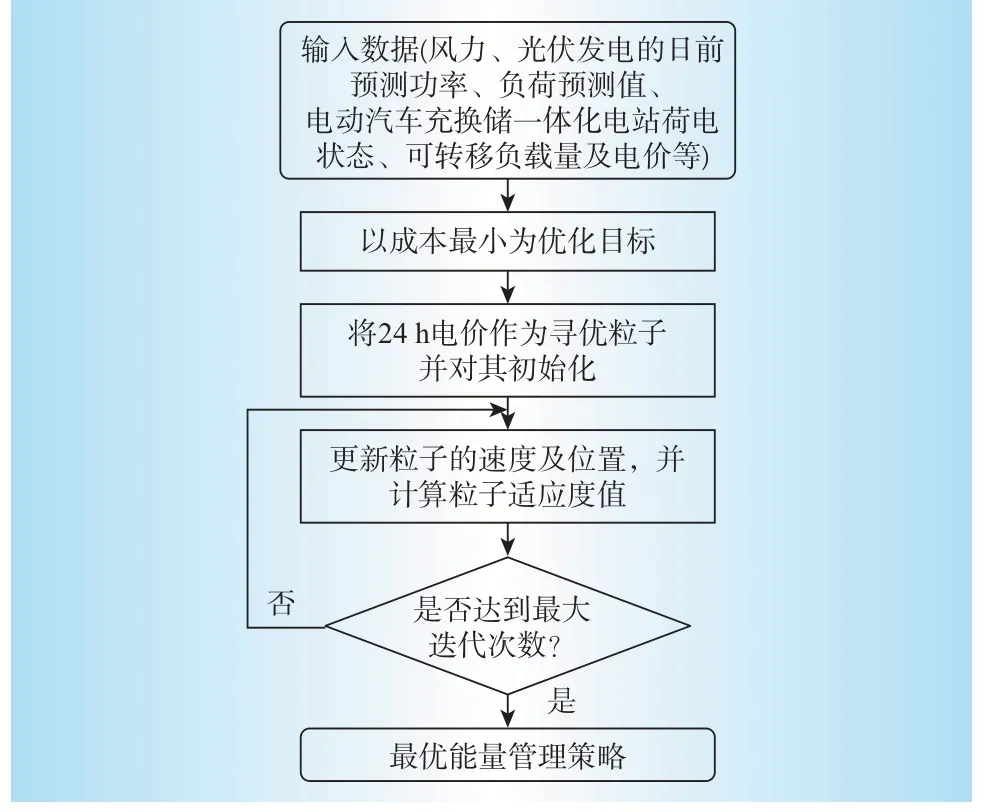
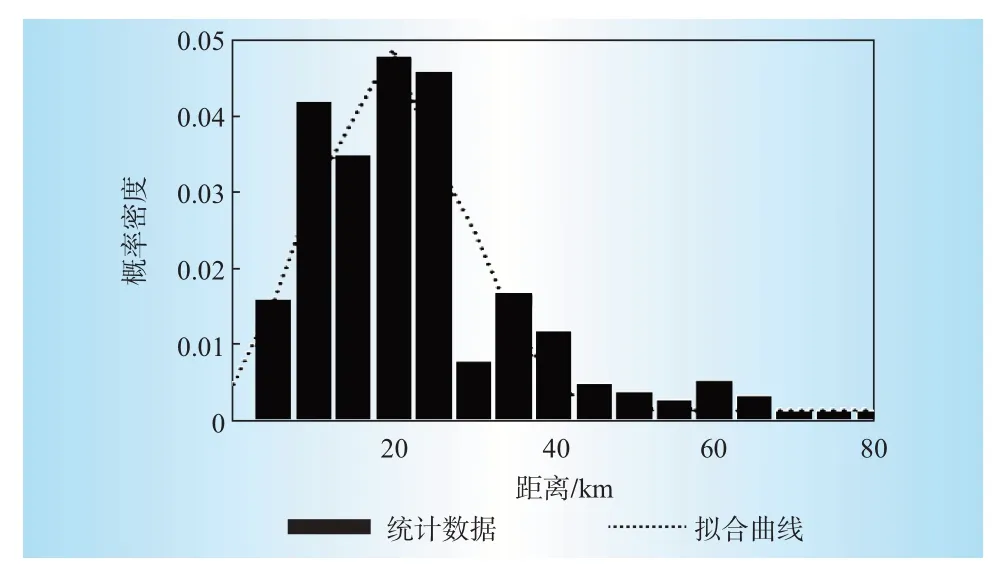
②若粗调系数Jcoarse低于粗调系数上限Jmax，即Jcoarse

③利用Ns个发电机组中选择的一个随机指数r，结合式（8）中得到的总的功率差，通过式（10）对每个发电机组的输出功率进行调整，并执行步骤④。

④若细调系数Jfine低于粗调系数上限J'max，即Jfine

⑤如果t

基于粒子群算法能够很好的解决提出的电网经济调度模型。

求解流程如图2所示。

图2 电动汽车负荷预测流程Fig.2 Electric vehicle load forecasting flow

3 仿真验证

本文将根据前面所述的模型，对某市经济开发区的电动汽车充放电进行预测，表1给出了不同用地的使用情况。而仿真平台主要采用windows7操作系统的高性能计算机。主要配置四核CPU、2.5 GHz主频、16 G内存、500 GB 硬盘。主要的仿真软件为MATLAB/simulink2013a软件。本节电动汽车数据来源于（2021版）江苏省南京市新能源汽车产业投资布局分析报告与《南京市打造新能源汽车产业地标行动计划》。对于风机、光伏、储能和可切负载的数据则是借鉴文献［13］和文献［14］中的相关数据人为选定的。对这些数据而言，可以进行变更，只需在算法中将相关数据对应替换即可，并不影响优化问题的求解过程。

表1 不同用地的相关参数Table 1 Relevant data of different areas

按照该市发展电动汽车的规划，预计到2030年，该市电动汽车的保有量大概为5.2 万辆。根据对该地区私家车日出行情况的调研，可知车辆的日均行驶距离为37.85 km。图3表示的是车辆从办公区到住宅区之间行驶距离的拟合情况，原始数据直接从园区的历史记录中获取。

图3 电动汽车预测结果对比Fig.3 Comparison of electric vehicle prediction results

通常情况下，不同用户的充电行为不相同，使得电动汽车的空间分布不同。电动汽车充电前剩余SOC阈值分别为90%、60%、30%时，住宅区私家车负荷曲线如图4所示。

图4 不同充电SOC 阈值选择下的负荷曲线Fig.4 Load curves in different charging SOC situations

由图4分析可知，住宅区的负荷一般高于办公区和娱乐区负荷。住宅区有2 个负荷高峰，随着选择SOC 阈值的降低，负荷由中午向夜晚转移。由此可得，电动汽车的充放电受用户充电行为所影响。

图5表示在图3所示的电动汽车接入情况下，含有电动汽车充换储一体化电站（正为放电，负为充电）、储能设备和可中断负载的调控量。设定在该仿真模型中，电动汽车充换储一体化电站、储能设备、可中断负荷及分布式电源所对应的最大容量分别为100 kW、60 kW、20 kW和10 kW。其中，9:00—11:00无exchange power 就代表该时间段内仅靠分布式电源出力（该阶段光伏出功与风机出功都足够大）与和储能设备出力，即可满足负载需求。图5 中对应各时间点的优化调度策略如下:对于风光等可再生能源而言，始终运行于最大功率点跟踪模式。充换储一体化电站在1:00—8:00、12:00—23:00都处于供电状态；储能设备在0:00—5:00、12:00—15:00 和23:00都处于充电状态，在6:00—8:00和16:00—19:00都处于放电状态，其余时间点既不充电也不放电；可中断负载在9:00—11:00 和17:00—20:00 都处于被切除状态，在其余状态都处于连接状态。

图5 日经济优化调度值Fig.5 Daily economy optimal dispatch value

表2 表示在表1 和图3 所示的电动汽车接入情况下，该系统分别在仅分布电源参与调度，分布式电源与可中断负荷调度，本文虚拟电厂调度策略等3类情况下的运行成本。

表2 调度策略运行成本比较Table 2 Cost comparison of scheduling strategies

从表2 可以看出，基于本文提出的虚拟电厂优化调度策略，该系统的用电运行成本降低了9.12%，运行更加经济。

4 结束语

本文提出一种针对电动汽车充换储一体化电站、可中断负荷以及分布式电站组成的虚拟电厂，以经济效益最大化为目标构建综合目标函数，通过确定电动汽车充放电功率大小、储能电池充放电策略和可中断负荷的调度策略，保证了多种微电源组合下经济、高效和低碳运行。该虚拟电厂模式正常情况下为一种纯用能负荷，也具备向电网反向馈电的能力，在形成一定规模的情况下，可作为一种高效率储能系统，实现调度层面削峰填谷、应急支撑的功能。该研究为打造国家电网公司区域协调控制系统虚拟电厂功能应用“可实行、可复制、可推广”的典范提供了理论依据。