考虑安全性与正常使用性能的大件车辆过桥评估方法
2021-07-24袁阳光周广利高文博韩万水王俊峰
袁阳光,周广利,高文博,韩万水,王 涛,王俊峰
(1. 西安建筑科技大学 土木工程学院,陕西,西安 710055;2. 山东省交通科学研究院,山东,济南 250102;3. 港珠澳大桥管理局,广东,珠海 519060;4. 长安大学公路学院,陕西,西安 710064)
大件运输车辆是用于大体积、不可拆解货物长距离转运的特殊运载车辆,包括几何尺寸超限与车质量超限 2种类型。根据陕西省2012年−2015年 3年的统计数据,大件运输车辆通行次数达到119 625辆,车质量超限14 094辆。大件运输车辆在助力国家重点项目建设的同时,对沿线公路桥梁养护管理、性能保持等提出了更高的要求,与常规卡车相比,质量超限大件运输车辆荷载水平更高且往往因重大项目建设刚性需求而拥有强制通行属性。鉴于超载车辆对沿线公路桥梁所构成的潜在威胁,质量超限大件运输车辆成为了通行审批工作中的难点,该类车辆的快速审批授权亦成为了社会关注的焦点问题[1]。在交通强国与智慧交通战略背景之下,迫切需要通过智能化大件运输车辆过桥评估管理系统的建立来满足大批量通行许可申请的快速处理,该类智能管理系统研发涉及两个关键任务,即车辆可通行性判定及如何让不具备通行权车辆具备通行资格。两个关键任务的解决须立足于构建合理的大件运输车辆过桥评估方法。
受大件运输车辆通行审批需求驱动,国内学者已经结合不同省份的工程实践,参考现行桥梁技术规范,对大件运输车辆过桥的可通行性判定及相关开展流程进行了研究[2−3]。然而,评估过程中普遍采用应力检算、裂缝宽度检算、荷载试验评定等技术手段,导致所形成的评估流程耗时繁琐,无法满足大批量、快速审批的工作要求,无法为大件运输智能评估管理系统的建立形成有效支撑。在国外,研究人员借助可靠度理论建立了适用于大件运输车辆的荷载及抗力系数评估方法(LRFR)[4−6]。但与国内学者开展的相关研究类似,评估方法主要集中于桥梁关键构件的安全性。
然而,从桥梁结构长寿命健康运营的角度考虑,大件运输车辆过桥通行审批时,可通行性判据不应仅仅局限于通行过程的承载能力极限状态安全性,尚应考虑正常使用极限状态要求,即车辆在通过桥梁之后不应由于遗留正常使用性能问题而造成结构预期使用寿命的明显缩短[7]。现有相关研究已经指出,正常使用极限状态失效事件发生频率更高且该类事件所导致的养护干预行为占据了结构养护成本支出的主体部分[8−9]。国内外学者在大件运输车辆过桥评估实践中,提出了如下式所示的荷载效应比较法[10]:

式中,SCTV、n、SD分别为大件运输车辆荷载效应、临界荷载效应比值及设计汽车荷载效应。在国内工程实践中,n最为常见的取值为1.0。在国外,式(1)被用于大件运输车辆快速评估系统的建立[11−12]。截至目前,正常使用性能要求的内涵及相关理论分析尚未在临界荷载效应比值n的取值过程中予以充分体现,导致当前研究中n取值主观性问题较为突出。近年来,桥梁结构正常使用极限状态可靠度分析理论的发展及相关成果的积累为该问题的解决提供了可能[8,13 − 15]。
迄今为止,能够用于支撑大件运输车辆智能评估管理系统构建、且同时考虑安全性及正常使用性能要求的车辆过桥评估方法在国内外研究中鲜见明确报道,以工程结构可靠度理论为依托,通过大件运输车载下桥梁关键构件承载能力极限状态可靠度分析及正常使用极限状态可靠度分析,对该问题进行深入探索,不仅具有明显的理论价值,同时具有广阔的应用前景。
在此,针对大件运输车辆过桥智能评估管理系统建立所要面对的两大问题,首先,基于可靠度理论形成大件运输车辆过桥评估方法框架,包括安全性评估方法与正常使用性能评估方法;其次,选择高速公路典型中小跨径桥梁进行案例分析;最后,在已有相关研究的基础上,形成大件运输车辆通行保障策略及实施流程。进而为国内大件运输车辆智能评估管理系统的建立提供参考。
1 大件运输车辆过桥评估方法框架
大件运输车辆过桥评估应重点关注设计活恒载比例较高、对活载较为敏感的中小跨径桥梁[1]。在以往大件运输车辆过桥评估工程实践中,所关注的桥梁结构力学性能包括抗弯性能、抗剪性能及变形性能等。然而,根据以往车辆荷载下梁式桥力学性能分析的相关成果及现行桥梁结构设计方法现状,中小跨径梁式桥的抗剪性能因其对应的脆性破坏模式,通常较抗弯性能具有更大的冗余度[2]。因此,在建立大件运输车辆过桥评估方法框架时,重点关注桥梁的抗弯性能,在后续具体评估方法建立时,同时,给出抗剪承载力评估的考虑原则。
图1给出了所构建的大件运输车辆过桥评估方法实施框架。根据图1,在车辆可通行性判定时,首先应当保证桥梁结构的安全性,在此基础上,进一步确保车辆通行后关键构件的正常使用性能。基于安全性及正常使用性能要求的评估方法建立均基于可靠度理论。对于中小跨径梁式结构,关键构件安全性评估方法的评估式为:
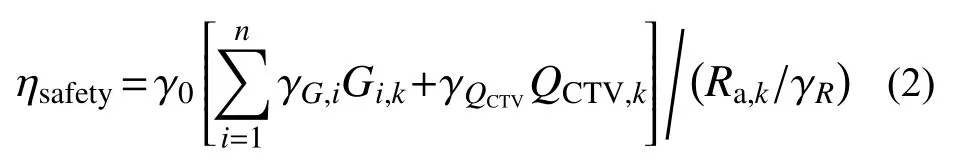
式中: ηsafety为安全评估指标,小于1.0时表示能够满足安全性要求; γ0、 γG,i、 γQCTV及 γR分别为重要性系数、第i项恒载效应分项系数、大件运输车辆荷载效应分项系数及抗力分项系数;Gi,k、QCTV,k及Ra,k分别表示第i项恒载效应标准值、大件运输车辆荷载效应标准值以及车辆通行时刻构件抗力标准值,具体取值原则参见文献[16]。需要指出,对于中小跨径梁式桥,质量超限大件运输车辆通行过程中实施交通管制的困难性不大,故式(2)中活载部分仅考虑大件运输车辆荷载效应,各分项系数取值将在大件运输车辆单次通行评估目标可靠指标取值分析的基础上,通过校准分析确定。
基于正常使用性能要求的评估方法采用临界荷载效应比值方法,车辆通行满足正常使用性能要求对应的条件为:
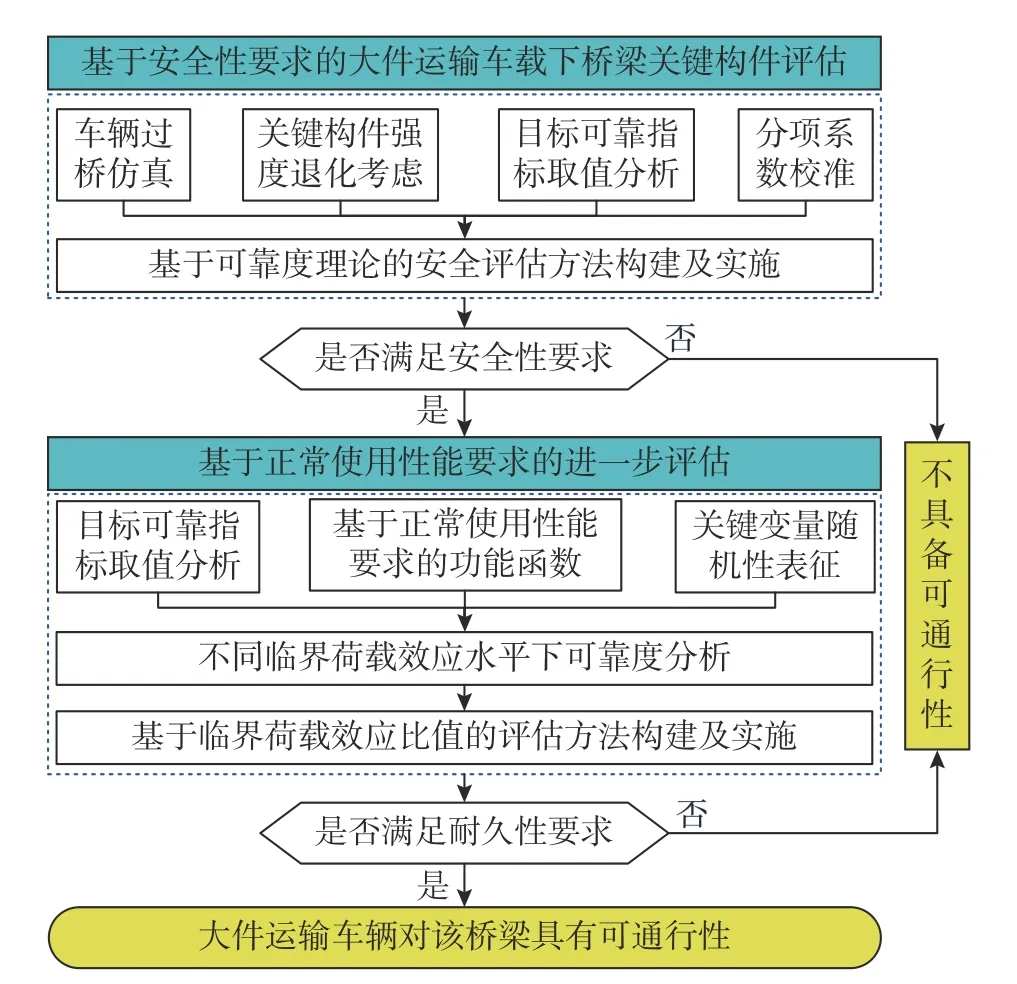
图 1 大件运输车辆过桥评估方法框架Fig.1 Method framework of bridge assessment under customized transportation vehicle

式中: ηserv为荷载效应比值;Qdesign、 ηcritical分别为构件的设计汽车荷载效应及临界荷载效应比值。后续分析中,将通过正常使用极限状态可靠度分析及目标可靠指标分析形成 ηcritical确定流程,具体而言,对于钢筋混凝土结构及预应力混凝土结构,将分别以裂缝宽度及混凝土底缘拉应力为特征指标构建正常使用极限状态功能函数。
需要指出,图1所示评估方法框架以大件运输车辆单次通行、单次评估、单次授权为导向,未采用基于总体样本分析的传统车辆荷载评估实施思路,主要由于传统思路无法兼顾大件运输车辆荷载的个体特性、无法满足单次通行授权评估工作需求,而在后续分析中,将引入荷载效应变异系数对大件运输车辆荷载随机性进行量化表征。
2 基于可靠度理论的关键构件安全性评估方法
首先,基于可靠度理论建立大件运输车载下桥梁关键构件的安全性评估方法。大件运输车载下桥梁结构性能仿真及构件荷载效应计算已在笔者已有研究中通过车-桥耦合分析系统的建立予以解决[17−18]。本文重点探讨安全评估目标可靠指标取值、构件强度退化的考虑及分项系数的校准。
2.1 安全性评估目标可靠指标
大件运输车载对于桥梁结构而言类似于一种偶然荷载,为确定其单次通行安全评估目标可靠指标,以1年为基准时间单位,将一年内通过桥梁的大件运输车辆与正常交通荷载考虑为混合荷载序列,如图2所示。
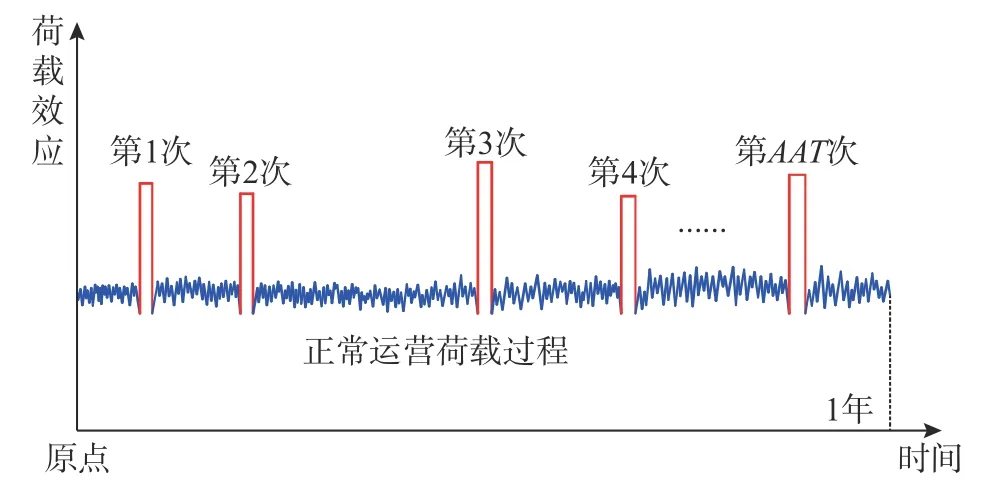
图 2 大件运输车辆与正常交通混合荷载序列Fig.2 Mixed load sequence by including customized transportation vehicle and normal traffic
记桥梁构件运营阶段的年目标可靠指标为βT,year,则对应的年安全概率为:
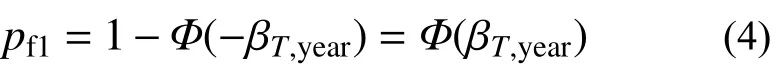
记正常运营荷载下桥梁构件的年目标可靠指标为 βyear,则正常运营荷载下桥梁构件的年安全概率为:

若一年内大件运输车辆荷载的通行次数为AAT,且记大件运输车辆单次通行目标可靠指标为 βT,safety,则在全年大件运输车载下桥梁构件的安全概率为:
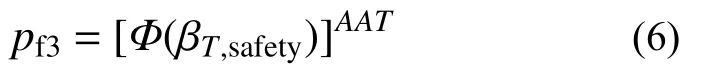
根据:

得到:
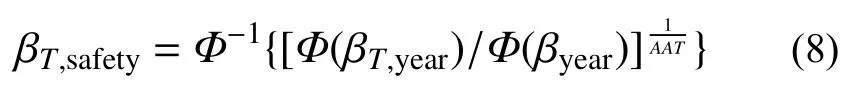
需要指出,为排除荷载水平较低、几何尺寸超限的大件运输车辆对分析过程的干扰,式(8)中的AAT仅考虑质量超限的大件运输车辆。
文献[16]通过考虑个体风险准则、社会风险准则、生活质量指标及总成本优化分析等,建议评估基准期为10年时,对安全等级一级、二级、三级的延性构件,评估目标可靠指标分别取为3.37、3.13与2.85,进一步根据不同时间尺度目标可靠指标的换算关系:
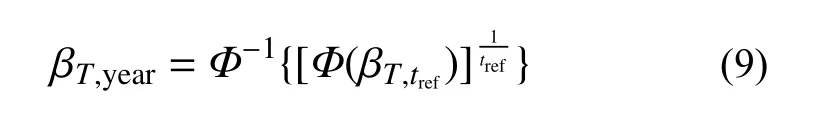
式中, βT,tref为任意基准期tref对应的评估目标可靠指标。对于一级、二级、三级延性破坏构件,βT,year分别为3.96、3.75与3.52。
图3(a)以一级构件为例,给出了 βT,safety随βyear的变化情况,可见当 βyear数值水平较小时,βT,safety随 βyear的增大快速下降,当 βyear足够大时,βT,safety逐渐趋于稳定。关于 βyear的取值,考虑一般的情形,根据现行设计基准期目标可靠指标及式(4)推定设计年目标可靠指标,进一步根据ISO 2394关于风险事件量化的建议,运营阶段容许失效概率可较设计阶段高一个数量级,由此确定一级、二级、三级构件 βyear分别为5.15、4.70及4.25[19−20]。图3(b)给 出 了 βT,safety随AAT的 变化,可见, βT,safety随AAT的增大而增大,且增长率随AAT的增大有所下降,该趋势意味着如果大件运输交通量较大,应当对评估方法适当收紧。
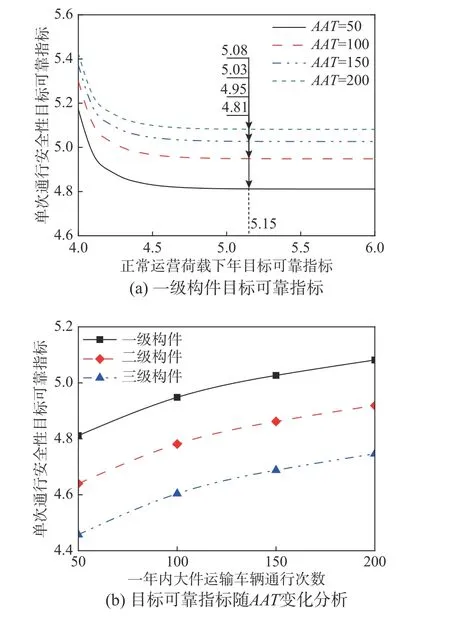
图 3 大件运输车辆过桥安全评估目标可靠指标Fig.3 Target reliability index of bridge assessment under customized transportation vehicle
以上关于评估目标可靠指标的分析主要针对抗弯性能,对于抗剪承载力安全性,由于剪切破坏属于脆性失效模式,故其安全评估目标可靠指标应高于抗弯承载能力评估。式(4)~式(9)所对应分析流程对于抗剪评估目标可靠指标选择同样适用。
2.2 构件强度退化考虑
大件运输车载下桥梁关键构件的安全性评估必须考虑构件的实际承载力水平。以《公路桥梁承载能力检测评定规程》(JTGT J21−2011)[21]评定结果作为构件承载力标准值,以混凝土构件为例:

式中:R(·) 为截面抗力效应函数;fd为材料强度设计值;adc、ads分别表示混凝土几何尺寸参数及钢筋几何尺寸参数; ξc、ξs、ξe分别表示混凝土截面折减系数、钢筋截面折减系数及承载力恶化系数;Z1表示承载力检算系数。李键等[22]研究了桥梁技术状况对大件运输承载力的影响,参考其研究成果,表1给出了一类、二类、三类桥梁对应的构件截面承载力修正系数取值。
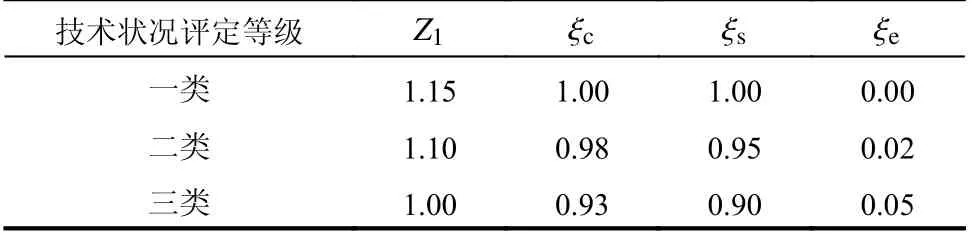
表 1 桥梁构件安全评估分项系数建议值Table 1 Proposed partial factors for the safety assessment of bridge component
需要指出,构件强度概率模型及退化过程本质上属于非平稳过程,且反复大件运输车辆荷载作用势必对构件强度退化规律造成影响,故在式(10)的基础上,仍有必要通过对大件运输车辆荷载反复作用的考虑,引入强度退化非平稳模型,以提高安全评估结果精度。
2.3 分项系数校准
分项系数校准的目的是保证评估方法在应用过程中具有统一的目标安全水平。通常情况下,认为恒载效应随机变量、大件运输车辆荷载效应随机变量服从正态分布,抗力随机变量服从对数正态分布,根据可靠度理论,分项系数表达式为[16, 23]:
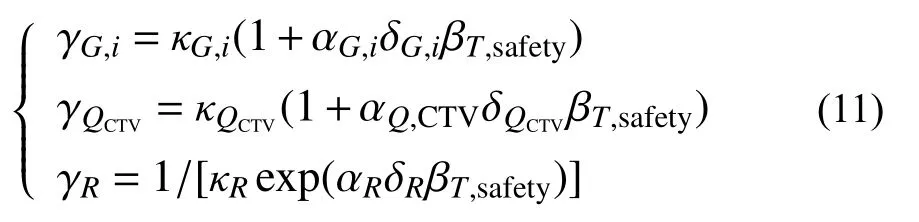
式中,κG,i、κQCTV=1.0 、κR=1.2262表示 随机变量均值与标准值的比值,对于自重引起的恒载效应,κG,i=1.0148 ; αG,i、 αQ,CTV、 αR为一次二阶矩灵敏度系数,根据ISO 2394的建议,对于控制性抗力参数与其他抗力参数分别取为−0.8、−0.32,对于控制性荷载效应及其他荷载效应分别取为0.7与0.28,考虑到中小跨径桥较高的设计活恒载比例,取 αG,i=0.28 、 αQ,CTV=0.7 、 αR=−0.8;δG,i=0.0431 、δQCTV=0.0368[24 − 25]、 δR为 随 机 变量的变异系数[17]。考虑到大件运输车辆通行评估实施过程中对桥梁技术状况的掌握水平,部分不确定性因素对抗力随机性的影响可予以排除,根据结构设计阶段 δR取值相关水平,选择大件运输车辆过桥评估过程中 δR=0.10。
根据图3(b)及以上分析,图4给出了安全评估分项系数的校准分析结果,可见各分项系数随AAT的变化趋势与目标可靠指标相同,对于一级、二级、三级构件及可能的AAT,恒载效应、大件运输车载效应及抗力分项系数范围分别为[1.069, 1.077]、[1.115, 1.131]及[1.165, 1.225]。
3 基于可靠度理论的关键构件正常使用性能评估方法
3.1 正常使用性能评估目标可靠指标
我国规范制定及修订过程中,已经对正常使用极限状态设计隐含可靠度水平进行了校准分析,发现正常使用极限状态可靠度水平不低于0.8,但与之对应的基准期信息并不明确。在此,对于大件运输车辆过桥评估时的正常使用极限状态目标可靠指标,采用JCSS的研究建议,年目标可靠指标取为 βT,annual=1.3[26]。在实际工程应用中,可结合JCSS相关建议及实际情况对大件运输车载下桥梁关键构件的年目标可靠度水平进行调整。进一步根据质量超限大件运输车辆的年预期交通量AAT,确定大件运输车辆单次通行时的正常使用极限状态评估目标可靠指标 βT,serv:
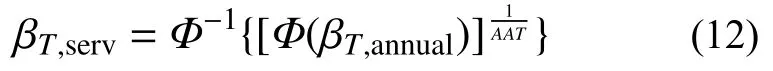
根据式(12),图5给出了不同AAT对应的βT,serv。
3.2 正常使用极限状态功能函数
考虑最为常见的3种中小跨径桥梁结构构件:1) 钢筋混凝土构件;2) 部分预应力混凝土构件;3) 全预应力混凝土构件。功能函数建立时,结合现行桥梁结构设计规范的要求,分别采用弯曲裂缝宽度及混凝土正应力作为钢筋混凝土构件(RC)及预应力混凝土构件(PC)的特征指标。
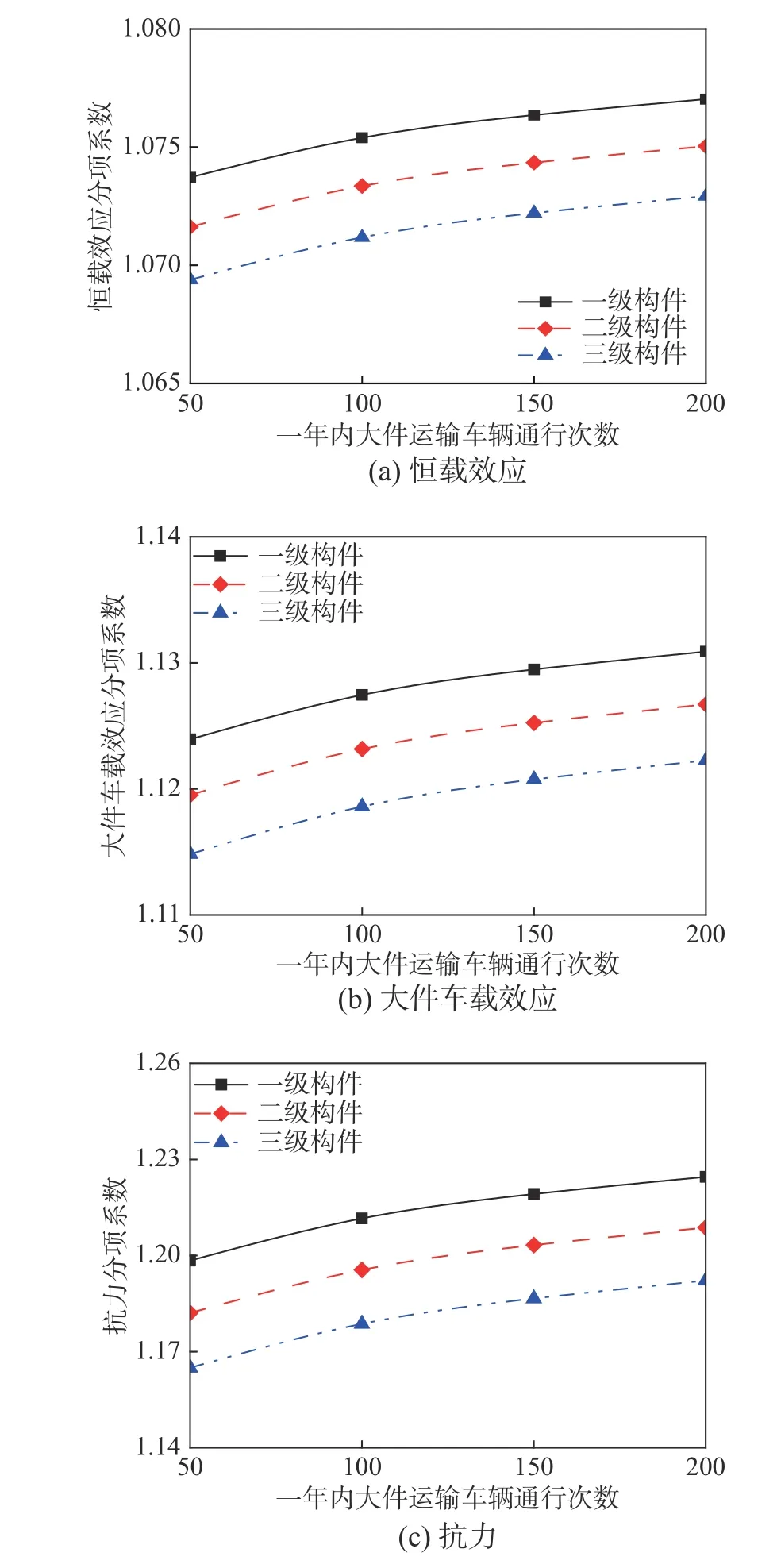
图 4 大件运输车载过桥安全评估分项系数Fig.4 Partial factors of bridge safety assessment under customized transportation vehicle load
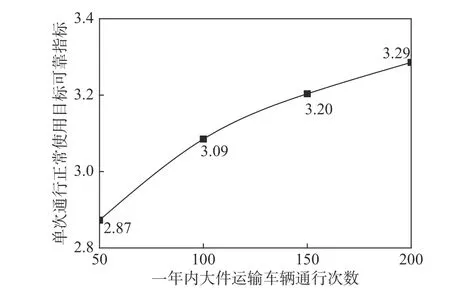
图 5 正常使用极限状态评估目标可靠指标Fig.5 Target reliability index of assessment for serviceability limit state
首先,根据弯曲裂缝宽度计算方法及控制准则建立RC构件的功能函数:
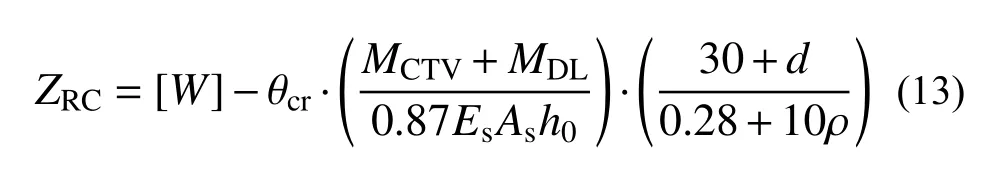
式中:ZRC、 [W] 、 θcr分别表示功能函数、容许裂缝宽度及计算模式不确定性系数;MCTV、MDL分别表示大件运输车辆正弯矩效应及恒载正弯矩效应;其余变量解释同《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362−2018)[27]。
RC构件的容许裂缝宽度通常在0.1 mm~0.5 mm,在此,根据我国桥梁设计规范取[W]=0.20mm,表2给出了国际上不同设计规范对容许裂缝宽度的规定。可见,我国对RC构件的裂缝宽度控制较为严格,在实际工程应用中适当放宽裂缝宽度是可行的。

表 2 钢筋混凝土构件容许裂缝宽度 /mmTable 2 Allowable crack width of reinforced concrete component
对于部分预应力混凝土构件及全预应力混凝土构件,根据关键截面混凝土应力控制方法建立功能函数:

式中:ZPC,部分、ZPC,全分别表示部分预应力混凝土构件及全预应力混凝土构件功能函数;ω为用于考虑构件技术状况退化的有效预应力损失百分比;ftk为混凝土抗拉强度标准值;其余变量解释同《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362−2018)[27]。基于现行桥梁规范建立式(13)~式(14)所示功能函数的目的为:确保相关研究成果能够最大限度地面向并服务于工程应用。
3.3 变量随机性及基于重要性抽样的可靠度分析
式(13)~式(14)功能函数中涉及变量较多,为实现正常使用极限状态可靠度分析,必须明确各变量的概率特性,通过对已有相关研究成果的总结,表3给出了随机变量的概率特性及分布参数信息[28 − 32]。

表 3 变量概率分布特性及分布参数Table 3 Probabilistic characteristics and distribution parameters of variables
采用重要性抽样对式(13)~式(14)进行可靠度分析,正常使用极限状态失效概率为:
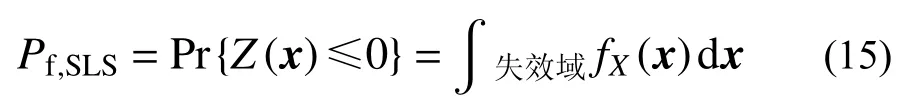
式中:x=(x1,x2,···,xm) 表示m维输入变量向量;fX(x)为联合概率密度函数。
引入示性函数:
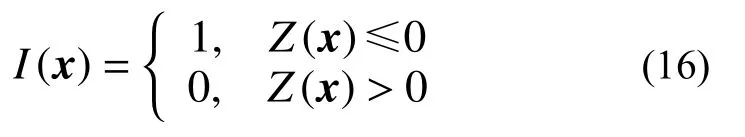
式(15)可改写为:
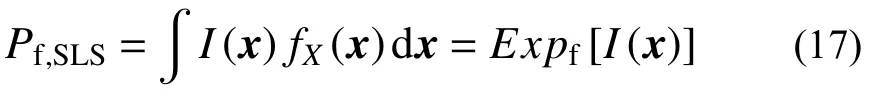
式中,Expf(·)为期望算子,为进一步提升抽样效率,引入满足归一化条件的重要性抽样密度函数:
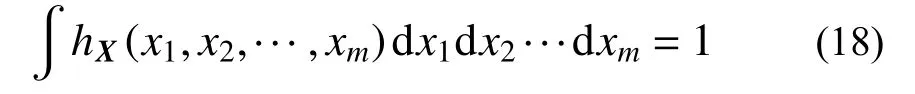
Pf,SLS可重新表示为:

在基于hX(x)得到独立同分布随机变量样本{x(1),x(2),···,x(N)}的前提下,失效概率的估计为[33]:

理论上,最优的重要性抽样密度是无法获得的,主要由于其确定需要借助待求解的真实失效概率,在此,近似认为重要性抽样密度为正态分布函数,变异系数取为原变量的1.0倍~2.0倍[34]。重要性抽样密度函数均值取为fX(x)的最大似然点,可通过以下数学规划问题的求解得到:

基于以上分析流程,开展不同大件运输车辆荷载效应水平下构件的正常使用极限状态可靠度分析,通过将分析结果与评估目标可靠指标βT,serv的对比,通过坐标比对寻找与 βT,serv对应的荷载效应比值,可确定特定目标可靠水平下式(3)所需临界荷载效应比值 ηcritical。
4 典型案例应用分析
4.1 典型中小跨径梁式桥
以部颁桥梁上部结构通用图中设计汽车荷载等级为公路-I级、斜交角0°、路基宽度24.5 m、左右幅分离的简支钢筋混凝土板桥(RCS)、预应力混凝土空心板桥(PCS)及预应力混凝土T梁桥(PCT)为研究对象,开展典型案例应用分析,构件重要性等级为一级。所选择的12座桥梁具体信息如表4。
图6~图7以其中4座桥梁为例,给出了不同主梁截面类型桥梁的横断面及截面受力钢筋配置信息。需要指出,在截面初始抗力计算时,将5 cm厚混凝土铺装考虑为了主梁顶板的一部分。考虑到大件运输车辆过桥速度缓慢,表4中设计汽车荷载效应未考虑冲击。根据表1所示承载力修正折减系数,确定一类、二类、三类桥梁的承载力折减系数分别为1.15、1.00及0.80。
4.2 基于正常使用极限状态可靠度的临界荷载效应比值
首先明确预应力构件可能的有效预应力损失百分比,导致预应力损失的主要因素为:1) 钢束张拉过程;2) 预应力钢束的松弛;3) 混凝土收缩徐变。近年来,国内外学者及设计规范提出了多种用于估算预应力损失的分析模型[35]。图8首先给出了根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62−2004)所得到的由钢束张拉及预应力钢束松弛导致的有效预应力损失百分比。

表 4 典型桥梁信息Table 4 Detailed information of typical bridges
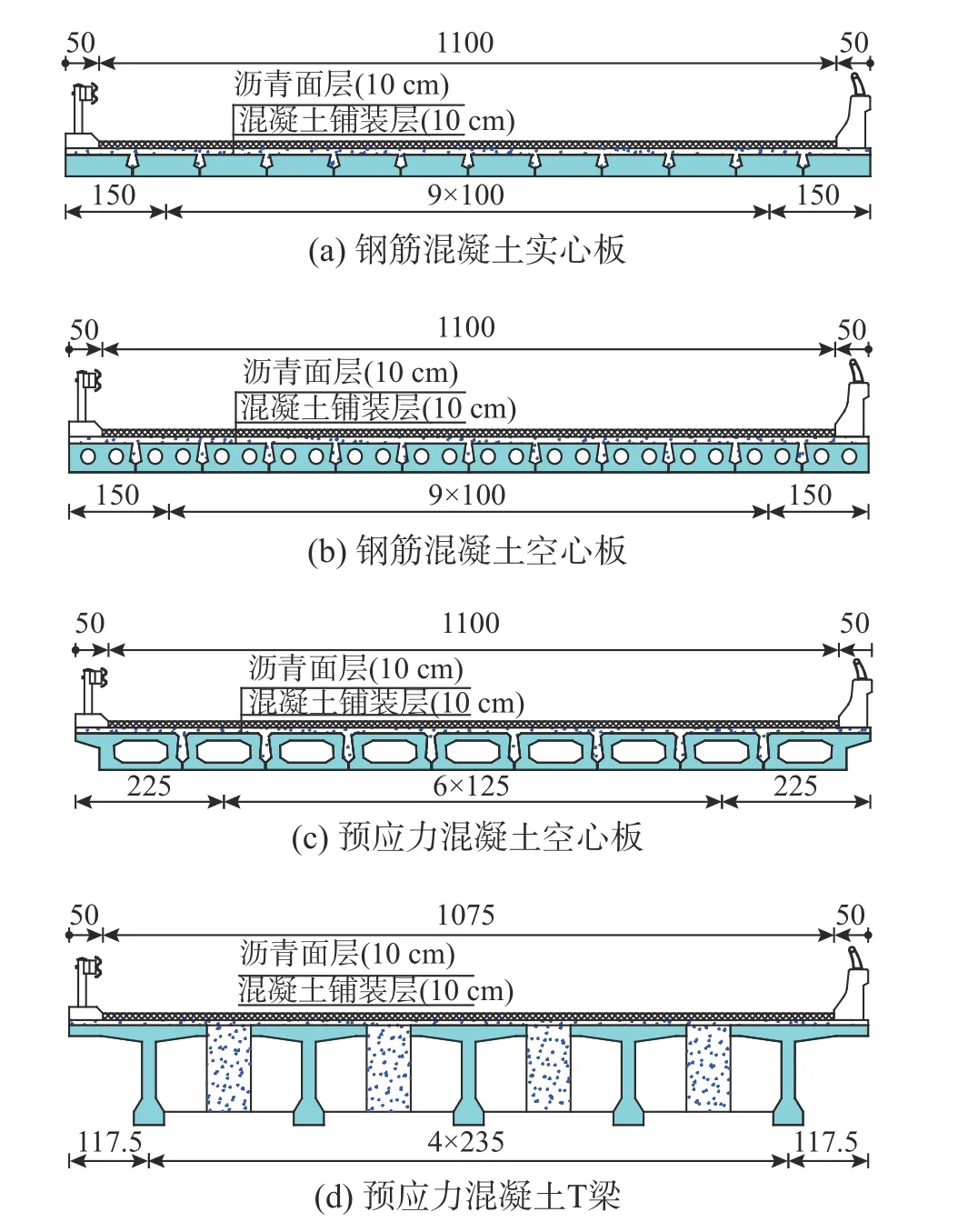
图 6 典型桥梁横断面 /cm Fig.6 Cross sections of typical bridges
进一步根据Biswal等的研究,当服役时间达到50年时,由混凝土收缩徐变所引起的有效预应力损失百分比可达到27%[36]。然而,考虑到我国大件运输线路选择时通常需要避开老旧桥梁及技术状况等级较低的桥梁,由混凝土收缩徐变引起的有效预应力损失百分比可选择一个较低的水平,在此,综合以上分析,建议ω的取值范围为20%~25%。
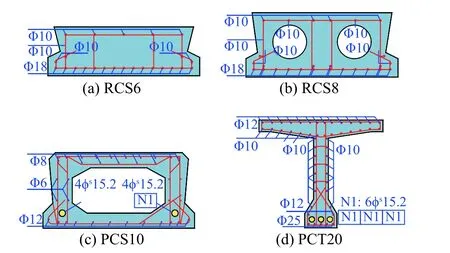
图 7 典型桥梁截面配筋 /mm Fig.7 Sectional reinforcement arrangements of typical bridges
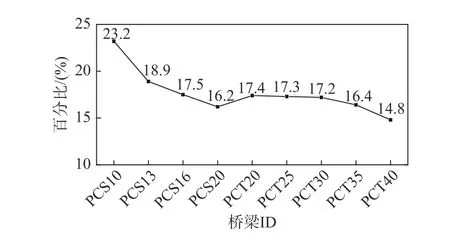
图 8 钢束张拉及预应力钢束松弛导致的有效预应力损失百分比Fig.8 Losing percentage of efficient prestress caused by tension stage and relaxation
在实际应用过程中,为提升大件车载作用下桥梁正常使用性能的评估精度,仍应借助不同的技术手段,提升对待评估桥梁预应力损失情况的估算精度。
图9以RC桥梁及PCS20为例给出了基于正常使用极限状态可靠度分析结果确定临界荷载效应比值的示意。表6进一步给出了12座桥梁在不同评估目标可靠指标下的临界荷载效应比值或取值范围。由图9及表6可知,随着跨径的增大,临界荷载效应比值无明显的变化规律,主要由于该分析结果受桥梁跨径、设计活恒载比例及截面配筋情况等多种因素共同影响,此外,预应力损失百分比对临界荷载效应比值影响比较明显,在实际工程中,为提升大件运输车辆过桥评估精度,应进一步加强对沿线桥梁有效预应力损失的估算。
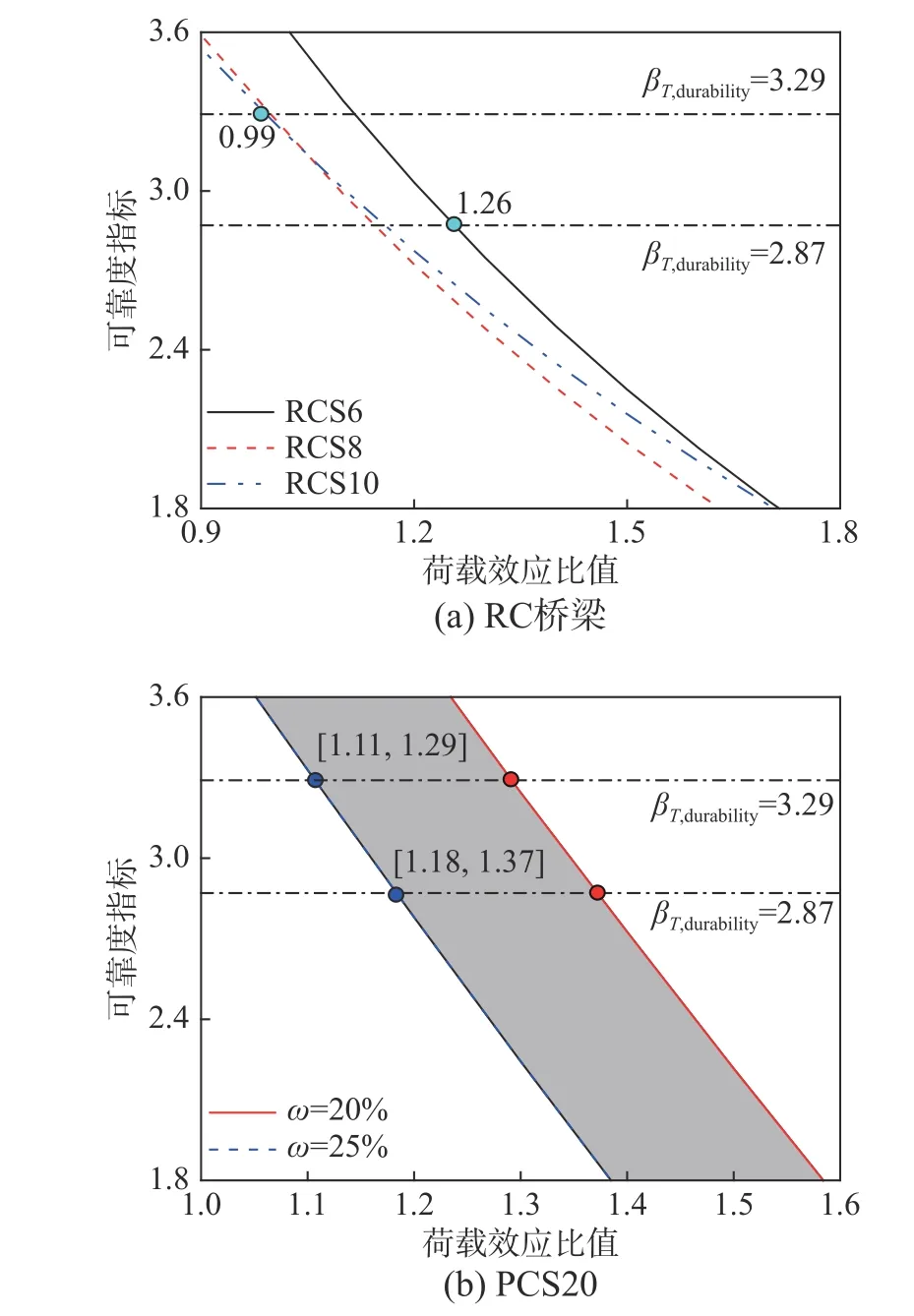
图 9 基于可靠度分析的临界荷载效应比值确定Fig.9 Determination of critical load effect ration according to reliability analysis
4.3 大件运输车辆过桥评估
结合图8及对应分析结果,考虑预应力混凝土空心板有效预应力损失百分比为25%,预应力简支T梁桥有效预应力损失百分比为20%,开展大件运输车辆过桥评估案例分析。大件运输车辆荷载信息如图10(a)所示,车货总重为523 t,图10(b)给出了采用大件运输车辆过桥分析系统分析该车辆通过PCT20的过桥场景,其中,为满足分析效率要求,基于梁单元建立结构有限元模型。鉴于现行规范对大件运输车辆过桥的通行轨迹要求,以12座桥梁的中梁为关键构件。
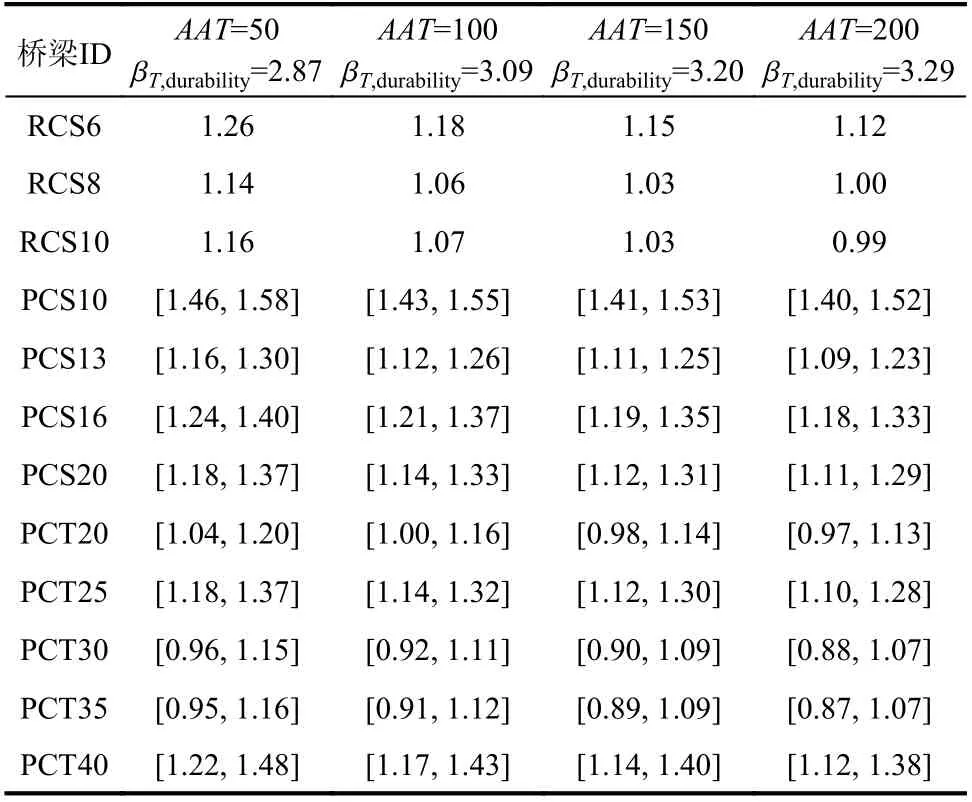
表 6 大件运输车辆过桥评估临界荷载效应比值Table 6 Critical load effect ratios for bridge assessment under customized transportation vehicle
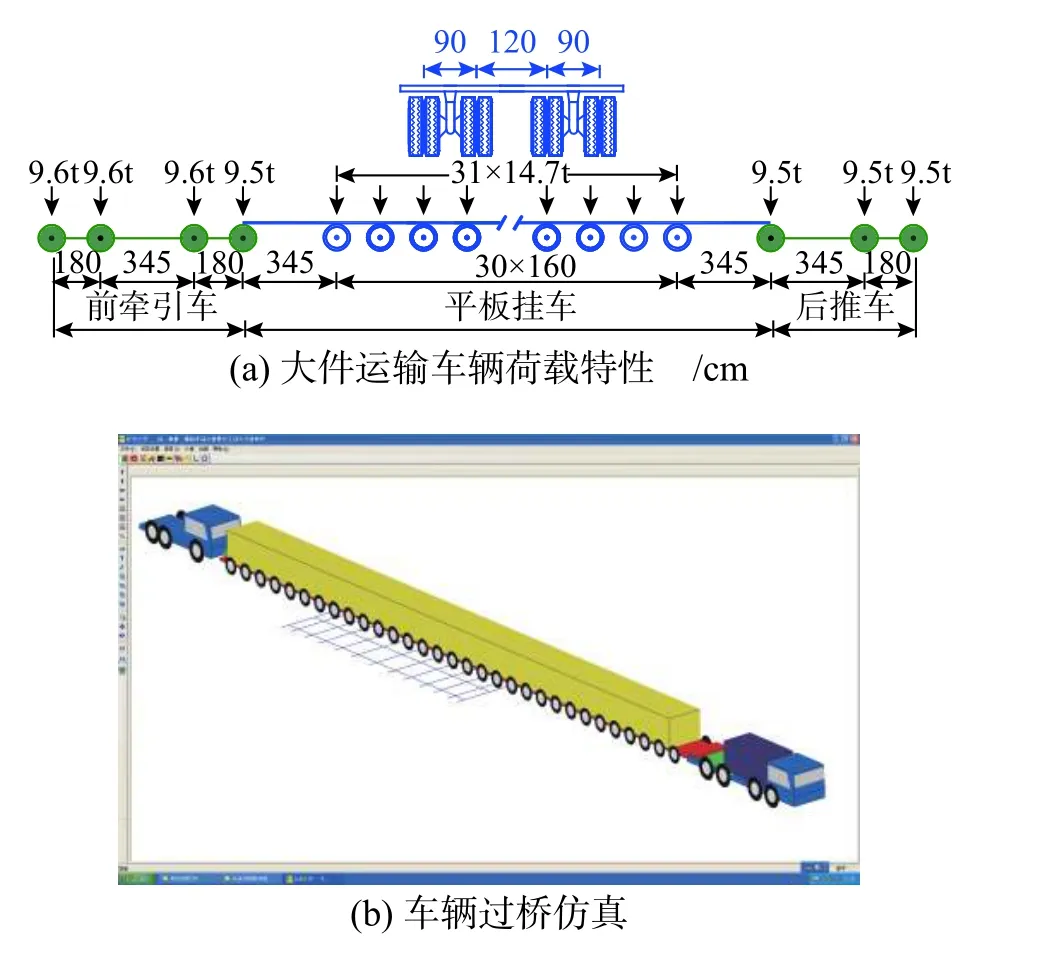
图 10 大件运输车辆荷载及仿真分析Fig.10 Customized transportation vehicle load and simulation analysis
根据图10(a)所示大件运输车辆对12座桥梁的加载分析结果,借助所建立的安全评估方法首先进行安全性评估,图11(a)给出了构件技术状况等级为二类时不同AAT对应的安全评估指标,可见当桥梁技术状况等级一定时,AAT对安全评估结果影响较小。图11(b)给出了AAT=200时,不同技术状况等级对应的安全评估指标,可见桥梁技术状况等级对安全评估结果影响显著,技术状况等级为三类时,部分桥梁安全评估指标超过1.0,不满足安全性要求。
根据图1所示流程,当大件运输车载下构件满足安全性要求时,应进一步开展正常使用性能评估,具体结果如图12。可见,从正常使用性能角度考虑,图10(a)所示大件运输车辆对12座桥梁的可通行性随着AAT的增加而下降,AAT=50、100时,各桥梁荷载效应比值分析结果均小于临界荷载效应比值,完全满足正常使用性能要求,当AAT=150、200时,PCS20荷载效应比值分析结果超过了与对应的临界值,大件运输车辆直接通行将导致PCS20关键构件正常使用性能无法保障。
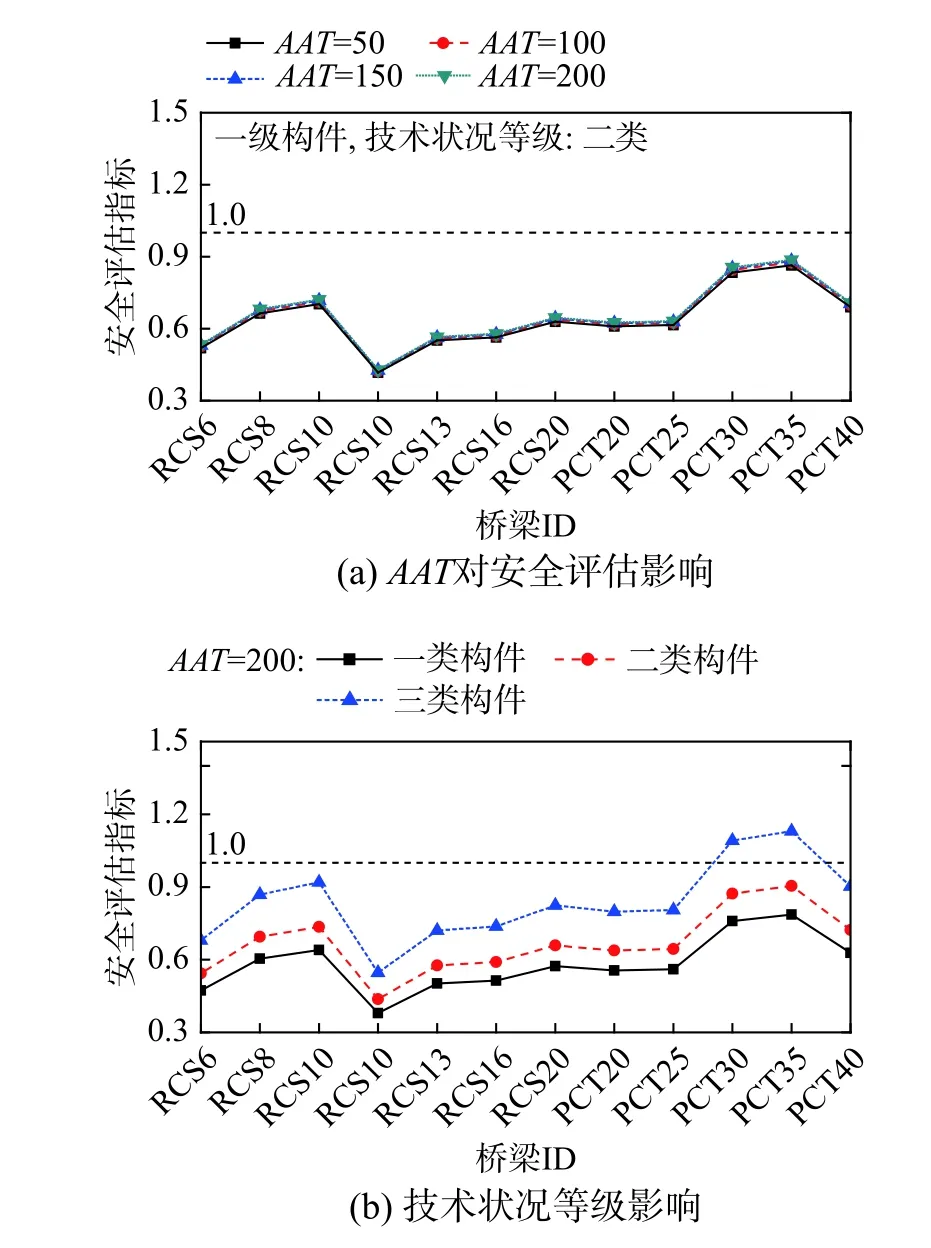
图 11 桥梁关键构件安全性评估Fig.11 Safety assessment of bridge key component
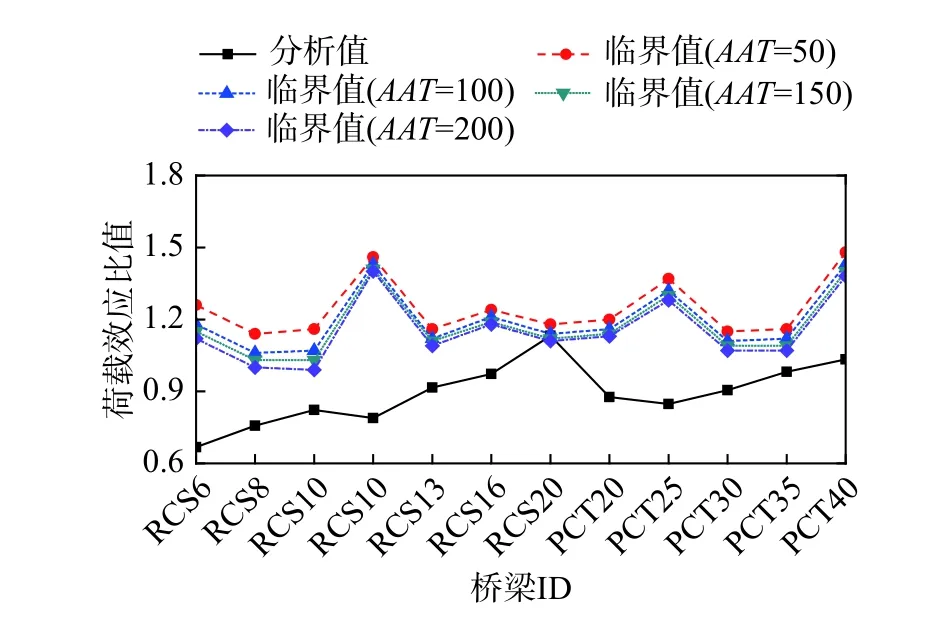
图 12 桥梁关键构件正常使用性能评估Fig.12 Serviceability assessment of bridge key component
5 结论
以可靠度理论为基础,考虑安全性与正常使用性能要求建立了大件运输车辆过桥评估方法,主要得到以下结论:
(1) 随正常运营荷载下构件年目标可靠指标的增大,大件运输车载单次通行下桥梁构件安全评估目标可靠指标快速下降,之后趋于稳定,随着大件运输交通量的增大,评估方法应适当收紧;
(2) 考虑年均大件运输交通量为50辆~200辆时,基于可靠度理论得到的中小跨径梁式桥恒载效应、大件运输车载效应及抗力分项系数取值范围分别为[1.069, 1.077]、[1.115, 1.131]及[1.165,1.225];
(3) 基于正常使用极限状态可靠度分析及目标可靠指标,可根据不同桥梁构件配筋信息等,可针对大件运输车辆荷载,确定基于正常使用性能的临界荷载效应比值,并用于可通行性快速判定;
(4) 大件运输车载下桥梁构件安全性评估结果受构件技术状况等级影响显著,年均大件运输车辆通行量的影响相对较小,但后者对构件正常使用性能评估结果影响显著;
(5) 尽管已经通过对安全性及正常使用性能要求的考虑,建立了大件车辆过桥评估方法,然而,该方法在不同地域特征下的应用及优化仍需进一步研究。
