足尺钢框架结构中楼板火灾行为数值分析

2021-07-24郭文轩李凌志简晓红张耕源赵行行

工程力学 2021年7期

王勇，郭文轩，李凌志,2，简晓红，马帅，张耕源，赵行行

(1. 中国矿业大学/中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，江苏，徐州 221008；2. 同济大学土木工程学院，上海 200092；3. 浙江瑞邦科特检测有限公司，浙江，杭州 310000；4. 中国建筑科学研究院有限公司，北京 100013)

目前，国内外学者对混凝土双向板火灾行为进行了大量试验和数值分析，取得了较多的研究成果[1−7]。值得指出的是，上述研究多针对简支板或连续板火灾行为方面[8−10]，对结构中混凝土双向板火灾行为数值方面相对较少。事实上，由于受火构件和相邻未升温结构单元的相互作用，结构中楼板火灾行为与单一板构件火灾行为不同，为了准确理解和掌握楼板及构件在结构中火灾行为，有必要对其力学机理进行深入分析。

近年来，国内外学者进行了一系列整体结构火灾试验。例如，1995年−1996年，英国Cardington的BRE火灾研究实验室对一足尺多层组合结构进行6次大型火灾试验[11]，研究表明，由于梁柱约束作用，火灾下楼板大变形阶段出现受拉薄膜效应，其有助于提高结构抗火性能。然而，上述研究主要侧重于火灾下压型钢板组合楼板力学行为，其相关研究结果无法完全用于指导钢筋混凝土楼板抗火设计。因此，2013年−2015年，董毓利课题组[12−14]对一足尺3层钢框架结构中楼板进行4次大型火灾试验，具体为顶层中区格和角区格两次火灾试验(钢梁未受火)、第二层四区格火灾试验(内部钢梁受火)和一层六区格火灾试验(内部钢梁受火)，研究表明受火跨位置、数量及钢梁是否受火对结构中楼板变形、裂缝和破坏模式等有重要影响。然而，安全起见，上述试验钢柱均未直接受火。Nguyen和Tan[15−17]开展了结构中组合板(缩尺)抗火性能试验，重点研究了(无)防火保护次梁和边界转动约束对火灾下组合楼板变形和破坏模式等影响规律。研究表明：次梁能够降低组合楼板跨中变形和提高其承载力(受拉薄膜效应)，转动约束易导致板角压碎和边梁出现较宽裂缝；当楼板跨中位移达到板厚时，开始出现受拉薄膜效应。然而，上述试验板均为缩尺板，致使组合板截面温度分布与实际结构不符。总之，上述结构或构件火灾试验复杂、周期长和费用高，进而在试验基础上，有必要对火灾下楼板温度、变形、薄膜机理和各构件内力发展规律开展深入数值分析。

目前，国内外学者对火灾下简支双向(组合)板温度、变形和薄膜机理等进行数值分析，指出火灾下简支双向(组合)板受拉薄膜效应有利于提高其耐火性能[18]。然而，上述研究主要针对简支双向(组合)板，未考虑不同边界条件对其薄膜机理影响，即忽略结构连续性和结构中其他构件约束作用。因此，王勇等[19]对火灾下单(双)向面内约束双向板力学性能开展数值分析，研究表明约束力水平、约束方向、配筋率和长宽比等对双向板裂缝间距、裂缝样式和板底爆裂等破坏模式有重要影响。此外，文献[10]研究了受火跨数量、位置、受火跨顺序、蔓延间隔时间、板厚和配筋率等对火灾下三跨连续双向板温度、变形、裂缝和破坏样式等影响规律。上述数值研究主要侧重于板构件，未考虑梁柱约束作用。实际上，Huang等[20]发展Vulcan软件，对火灾下足尺组合结构中楼板变形和薄膜机理等结构行为进行数值分析，重点研究了几何(非)线性对火灾下组合楼板变形行为和薄膜机理的影响规律，并指出单(双)向曲率变形对薄膜拉力产生及楼板抗火性能的影响规律。Ellobody和Bailey[21]采用ABAQUS软件，研究了不同火灾蔓延工况(不同火灾区域和火灾蔓延时间间隔)对结构中后张拉混凝土楼板变形行为的影响规律，研究表明楼板最大变形可能发生在火灾蔓延工况或多房间同时受火工况，结构设计时应考虑火灾蔓延工况。然而，不同火灾工况下楼板薄膜机理和梁柱构件内力发展规律并未给出。Nguyen和Tan等[15−16]采用ABAQUS软件，结合热弹塑性损伤本构和S4R壳单元，对结构中组合楼板温度、变形和梁板主应力分布等进行数值分析，数值表明次梁对组合楼板内钢筋应力分布和幅值及最终破坏模式(钢筋断裂位置)有重要影响，即跨中钢筋断裂(无次梁时)和边梁附近钢筋断裂(有次梁时)。Gernay和Khorasani[22]采用SAFIR软件，结合结构性能化抗火设计目标，对不同火灾工况下(单个房间受火、火灾蔓延和钢柱倒塌后受火)钢框架结构中组合楼板变形、薄膜机理、钢梁轴力和弯矩等进行分析；研究表明在性能化抗火设计时，应充分发挥受拉薄膜效应对提高结构抗火性能的有利作用，特别是钢柱破坏后的结构整体稳定性方面。然而，上述研究主要侧重于火灾下组合(预应力)楼板力学行为，所得结论能否用于指导钢筋混凝土楼板抗火设计还有待于深入研究。同时，有必要研究受火板格位置和数量以及钢梁是否受火对结构中各(未)受火板格薄膜效应发展及分布规律。

基于上述研究，本文采用Vulcan程序，对董毓利课题组[12−13]顶层和第二层楼板火灾试验进行数值分析；研究混凝土膨胀应变对火灾下结构中构件变形的影响规律；分析受火跨数量和位置对结构中楼板裂缝、薄膜机理和弯矩分布等影响规律；研究结构中钢梁和钢柱的内力发展趋势。本研究有助于理解火灾下结构构件间相互作用、传力路径及内力重分布行为，为结构性能化抗火设计提供数值参考。

1 试验板简述

1.1 试件板

文献[12 − 13]对一足尺3层钢框架结构中的顶层(中区格和角区格)和第2层楼板(2×2区格)进行火灾试验研究，试验楼为典型钢框架结构，由楼板、钢梁、钢柱以及填充墙组成，如图1(a)所示。如图1(b)所示，每层均为3×3跨，每跨为4500 mm×4500 mm，图中给出每个板格(A～I)、钢梁名称(L1～L12)和钢柱名称(如A1～A4)。

对于顶层，分别开展两次试验，即角区格(A)和中区格(E)，所有钢梁均未受火[12]；对于第二层楼板，受火区格为A、B、D和E四个区格，内部四个钢梁受火[13]。为便于表述，分别定义为试验I、II和III。所有试验柱和节点均未直接受火。

1.2 试验方案

对于试验I、II和III，均为自行设计火灾试验炉，试验炉外围钢梁、所有钢柱及梁柱节点均不受火；对于试验III，炉内4个钢梁均受火。试验前，楼板放置砂袋模拟2.0 kPa活荷载。

对于每试验，沿炉墙均匀布置若干K型热电偶测量炉温，数值分析时采用炉温平均值；沿板厚布置K型热电偶，用于测量混凝土及钢筋温度。采用差动式位移传感器测量变形。所有数据采用安捷伦数据仪进行采集，采集时间间隔15 s。

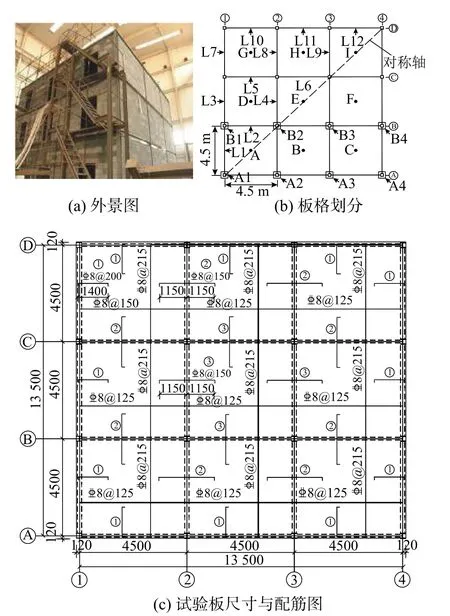
图 1 钢框架结构Fig.1 Steel-framed building

1.3 试验结果

1)平均炉温-时间曲线

三试验平均炉温-时间曲线如图2所示。可知，三炉温曲线均低于ISO834标准升温曲线，试验I、II和III停火时间分别为270 min、300 min和290 min，且平均最大炉温分别为881 ℃、890 ℃和787 ℃。

2)构件温度-时间曲线

图3为距板底(0 mm)不同位置处混凝土试验温度-时间曲线。可知，对于试验I、II和III，停火时，板底(板顶)最大温度分别为732.9 ℃(192.6 ℃)、733.7 ℃(231.1 ℃)和670.2 ℃(214.5 ℃)。明显地，由于较高炉温，试验I和II板温度梯度大于试验III。

图4(a)～图4(c)为试验I、II和III板底(顶)钢筋平均温度-时间试验关系曲线和计算曲线对比，图4(d)为试验III内受火钢梁L2上翼缘、腹板和下翼缘温度-时间试验曲线和计算曲线对比。可知，停火时，试验I、II和III中板底(顶)钢筋最大平均温度分别为632.1 ℃(231.8 ℃)、645.7 ℃(281.8 ℃)和585.3 ℃(179.1 ℃)。此外，停火时，试验III中钢梁L2截面平均温度为698.6 ℃。

图 2 三试验平均炉温-时间曲线Fig.2 Average furnace temperature-time curves of three tests

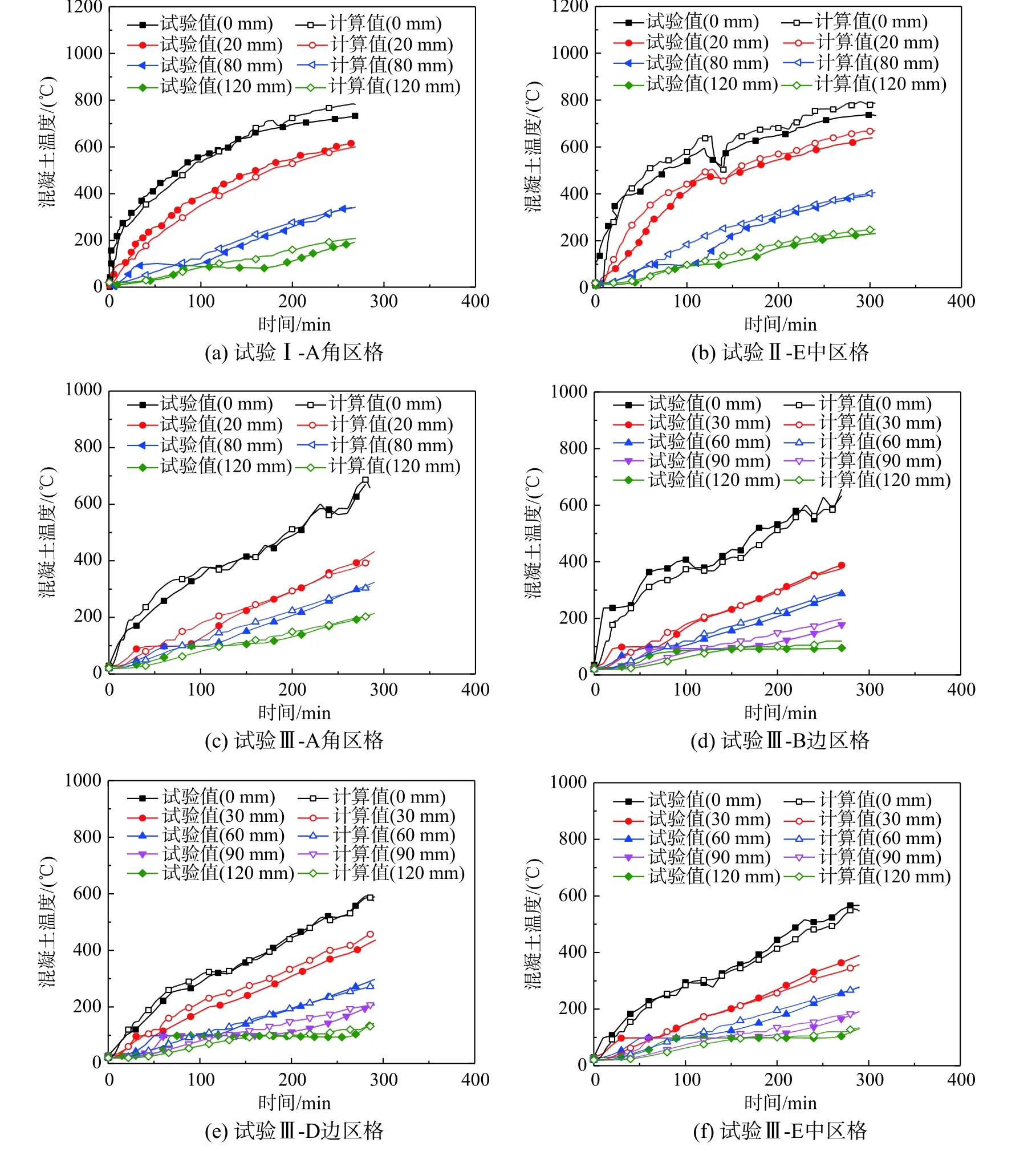
图 3 试验板混凝土温度场计算结果与试验结果对比Fig.3 Comparison of predicted and tested temperatures of concrete tested slabs

3)跨中挠度-时间曲线

图5为三试验中各受火板格跨中挠度(平面外位移)-时间试验曲线和计算曲线对比。

一方面，对比可知受火位置和数量对楼板变形趋势有重要影响，如试验III中，四区格跨中变形出现不同时长的变形平台，如A区格(50 min～80 min)、B区格(100 min～160 min)、D区格(66 min～155 min)和E区格(35 min～130 min)。而试验I和II中两板格跨中变形未出现变形平台。另一方面，停火时，试验I和II跨中变形为−137.8 mm和−113.4 mm，而试验III中A、B、D和E四区格跨中变形分别为−177.7 mm、−110.8 mm、−137.8 mm和−126.9 mm，均未达到变形破坏准则(l/20)。

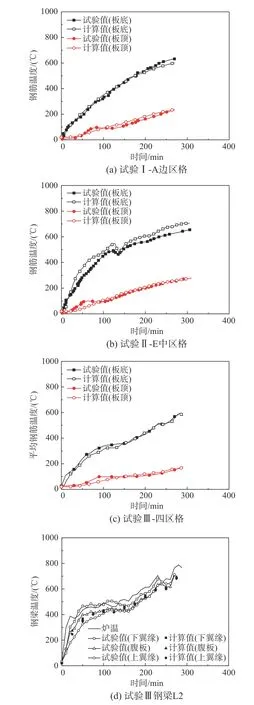
图 4 试验板温度场钢筋(梁)计算结果与试验结果对比Fig.4 Comparison of predicted and tested temperatures of concrete tested slabs

此外，图5(b)计算结果和试验结果有一定差别，原因可能在于分开进行角区格和中区格火灾试验，角区格试验后，中区格出现少许裂缝[12]，上述裂缝可能对板温及变形有一定影响。由于模型限制，分析时未考虑上述行为影响，这一点有待研究。

2 数值模型

采用Vulcan程序，对框架结构中楼板进行温度场模拟、变形和力学机理分析。温度场分析时，沿板厚划分24个矩形单元，如图6(a)所示；其中，混凝土表面辐射系数取值为0.8，火焰辐射系数取值为0.75，表面吸收系数为1.0。混凝土热工性能采用EC2模型[23]。

如图6(b)～图6(f)所示，结构分析时采用9节点厚板单元(几何非线性)，每单元9个高斯点G1～G9，楼板划分225单元(如编号17～21)，沿板厚划分16层；钢梁采用杆单元，且每个钢梁沿跨度方向划分为5个单元(如单元编号1～5)，沿其截面方向划分为26单元；每钢柱沿高度方向划分为4单元。除特殊说明外，高温混凝土和钢筋(钢材)力学性能均采用EC2模型，两者粘结性能良好[23]。此外，不考虑楼板和钢梁两者粘结滑移。计算时，采用经典弥散裂缝模型模拟混凝土开裂，即采用混凝土最大拉应变破坏准则，即当任一高斯点上主应变超过最大拉应变则发生开裂。当一个方向开裂后，认为混凝土是正交各向异性材料。在单向开裂混凝土继续加载，如果在垂直于裂缝方向上的拉应变超过最大拉应变，则发生双向裂缝形式[20]。

对于试验III，数值分析时，中柱所受初始集中荷载为125 kN，边柱初始集中荷载为62.5 kN，角柱初始集中荷载为31.25 kN。此外，如图6(g)所示，采用两混凝土热膨胀应变[23−24]，重点研究其对结构中楼板变形行为的影响规律。

3 计算结果

3.1 温度分析

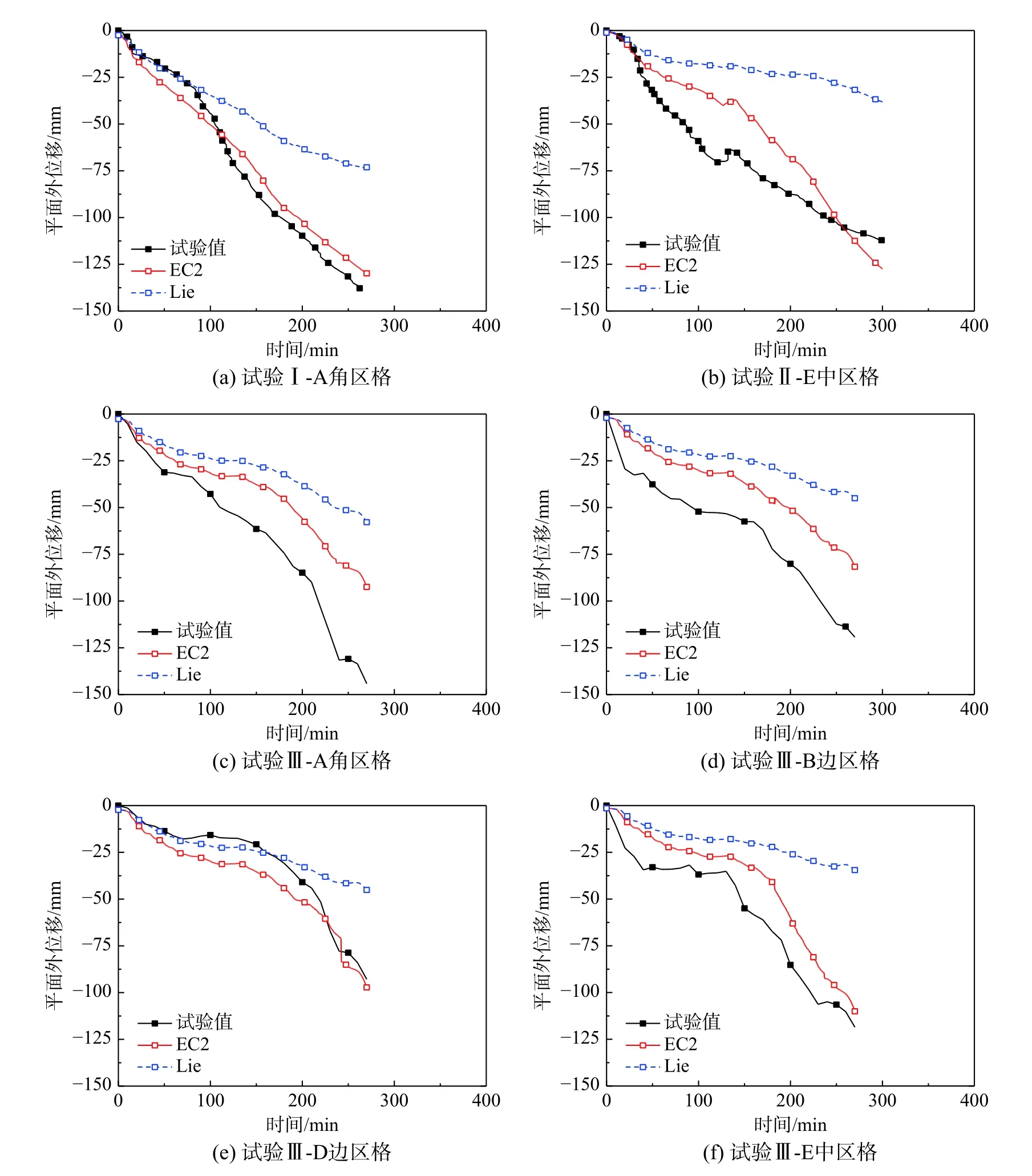
图 5 试验板变形计算结果与试验变形对比Fig.5 Comparison of predicted and tested deflections of concrete tested slabs

图3和图4为混凝土、钢筋和钢梁温度场计算结果和试验结果对比情况。可知，有限元模拟结果与试验结果吻合较好，变化趋势较为一致，温度分析较为合理。

3.2 裂缝分析

图7(a)～图7(c)为试验I、II和III板顶试验裂缝与数值分析所得弥散裂缝对比情况。可知，对于每个试验工况，弥散裂缝与试验板裂缝形式较为一致。

对于试验I，A角区格整体表现为对角U型裂缝，即靠近两内边梁位置裂缝较多(负弯矩作用)，临近角柱位置多为短小斜裂缝，板中区域裂缝较少。对于其他未受火板格，文献[12]未给出；计算表明两相邻边区格(D和B)和中区格(E)会产生较多裂缝，原因在于受拉薄膜效应和热膨胀作用，具体见下述。同时，对于其他较远板格，基本没有裂缝。数值分析表明，受火板格A板边区域(高斯点)出现双向弥散裂缝，板中区域未开裂，且非受火D和B板格多为单向弥散裂缝，可见模拟结果能够反映试验板整体裂缝分布。此外，可见在灾后修复时，除了对受火跨进行加固，也要对相邻非受火区格裂缝采取措施，特别是耐久性方面。

图 6 试验板温度和结构分析单元模型 /mmFig.6 Element models used in the temperature and structural analysis of tested slabs

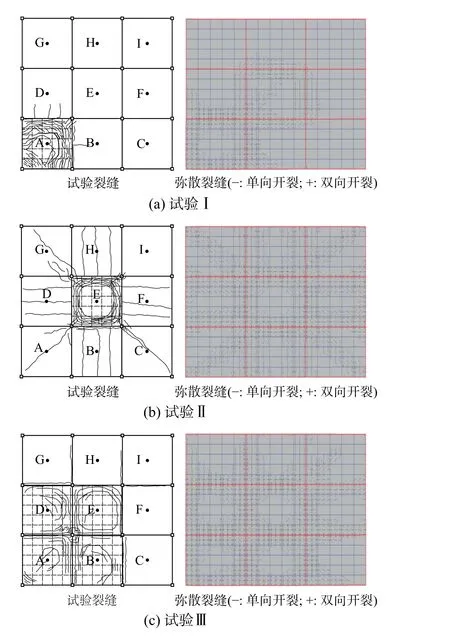
图 7 三试验裂缝与弥散裂缝对比Fig.7 Comparison between the experimental cracks and predicted smeared cracks of three tests

对于试验板II，弥散裂缝样式和试验结果基本吻合(见图7(b))。具体地，中区格板顶为环形裂缝(负弯矩)，且跨中区域裂缝较少(正弯矩)；此外，非受火角区格(A、C、G和I)出现45°对角线裂缝，且边区格(B、D、F和H)出现若干条平行裂缝。数值表明，受火板格E周边出现较多双向弥散裂缝，跨中区域无弥散裂缝，其余非受火板格为单向弥散裂缝，最终形成沿板跨方向或45°方向通长裂缝。主要原因在于中区格温度较高，向外膨胀；其他板格温度较低，对中区格产生较强约束作用，进而非受火板格产生拉应力而开裂，后续薄膜机理分析也证明了这一点。

对于试验III，弥散裂缝样式基本较为合理(见图7(c))，受火跨基本上表现为三种裂缝样式，即对角裂缝(角区格)、对边U型裂缝(边区格)和环形裂缝(中区格)，且裂缝集中在内支座位置(负弯矩)，数值结果表现为双向弥散裂缝。一方面，跨中区域裂缝相对较少，原因在于受拉薄膜效应相对较小(见下述)。另一方面，对于非受火区格，裂缝集中在钢梁上部楼板区域和板格内部，数值分析表现为少许双向弥散裂缝(钢梁顶部楼板)和较多单向弥散裂缝(板格内部)。

总之，在结构抗火设计中，应考虑受火跨数量和位置对各板格裂缝分布影响，且灾后对各板格采用相应加固方法。

3.3 变形分析

各受火板格变形计算结果与试验结果对比如图5(a)～图5(f)所示。可知，计算变形和试验结果总体吻合较好。对于试验III，与试验变形相比，计算变形总体偏小，原因可能在于膨胀应变取值。对比可知，混凝土热膨胀应变对受火板格变形有决定性影响，即较大膨胀应变引起较大跨中变形，特别是约束作用较强中区格。例如，对于试验II(III)的中区格，停火时，EC2和Lie两模型所得计算变形值分别为−127.5 mm(−38.2 mm)和−110.1 mm(−34.5 mm)。可见，降低混凝土热膨胀性能或采用热膨胀性能较小混凝土，有助于降低构件变形和提高其抗火性能。

图8(a)～图8(d)为试验III三钢梁平面外水平和竖向变形计算值和试验值对比情况。对于未受火边梁L1，计算值和试验值吻合较好。由图8(c)和图8(d)可知，两钢梁位移-时间计算曲线与试验曲线差异较大，主要原因在于钢梁采用杆件单元模型，无法准确模拟钢梁局部屈曲行为、节点上下翼缘断裂行为和节点处螺栓滑移等，模型有待于改进和细化(如壳单元)。值得指出的是，钢梁变形准确模拟(塑性铰)对楼板薄膜机理及破坏模式产生有重要影响，且涉及钢梁和楼板破坏顺序。具体地，钢梁过早破坏，楼板失去有效支撑，其不会产生薄膜效应，否则其会产生薄膜效应[25]。

此外，对比可知，混凝土膨胀应变(EC2和Lie)对钢梁变形有一定影响，但相对较小。

3.4 楼板薄膜机理

在变形分析基础上，对三试验中(非)受火区格薄膜机理进行对比分析，如图9(a)～图11(d)所示。值得指出的是，对于每板格中薄膜效应(单位：N/mm)，红(蓝)色代表受拉(压)薄膜效应，线长度表示薄膜大小。清晰可见，图中0 min薄膜效应图数据缩小10倍，其余图中数据缩小100倍。

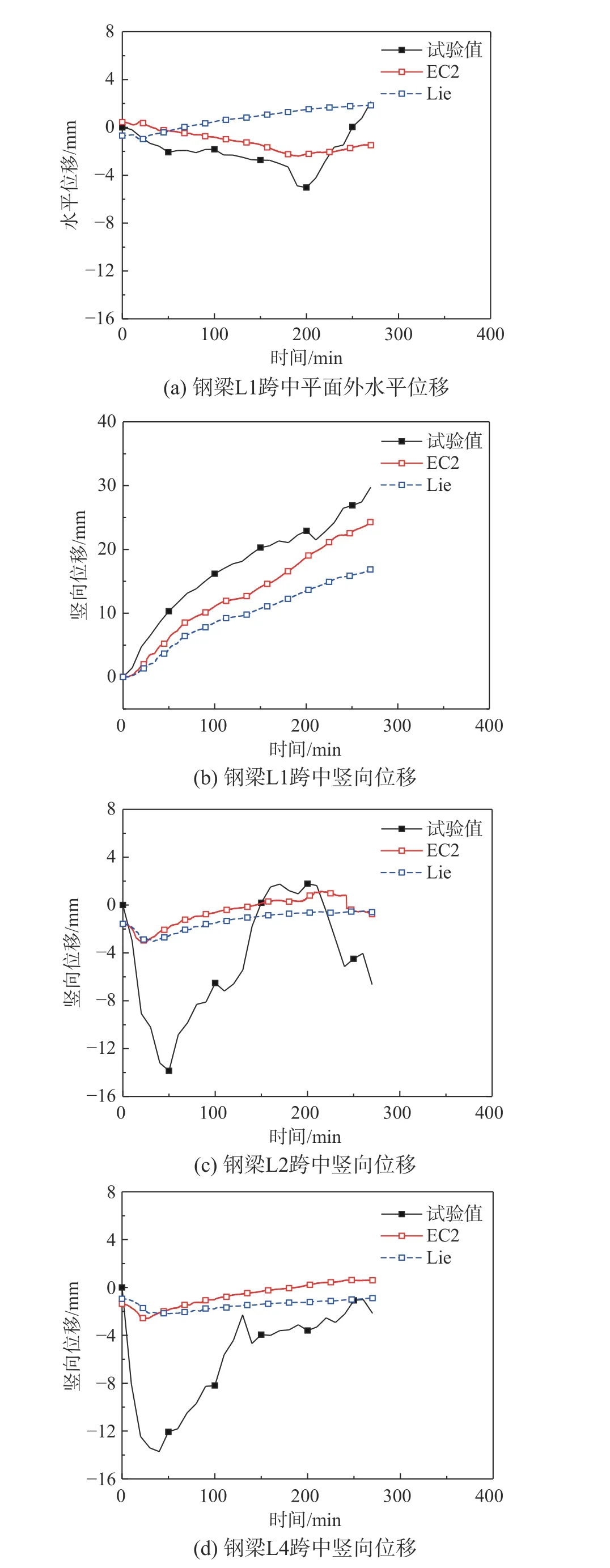
图 8 钢梁位移-时间计算曲线与试验曲线对比Fig.8 Comparisons of the predicted and experimental deflections of the steel beams

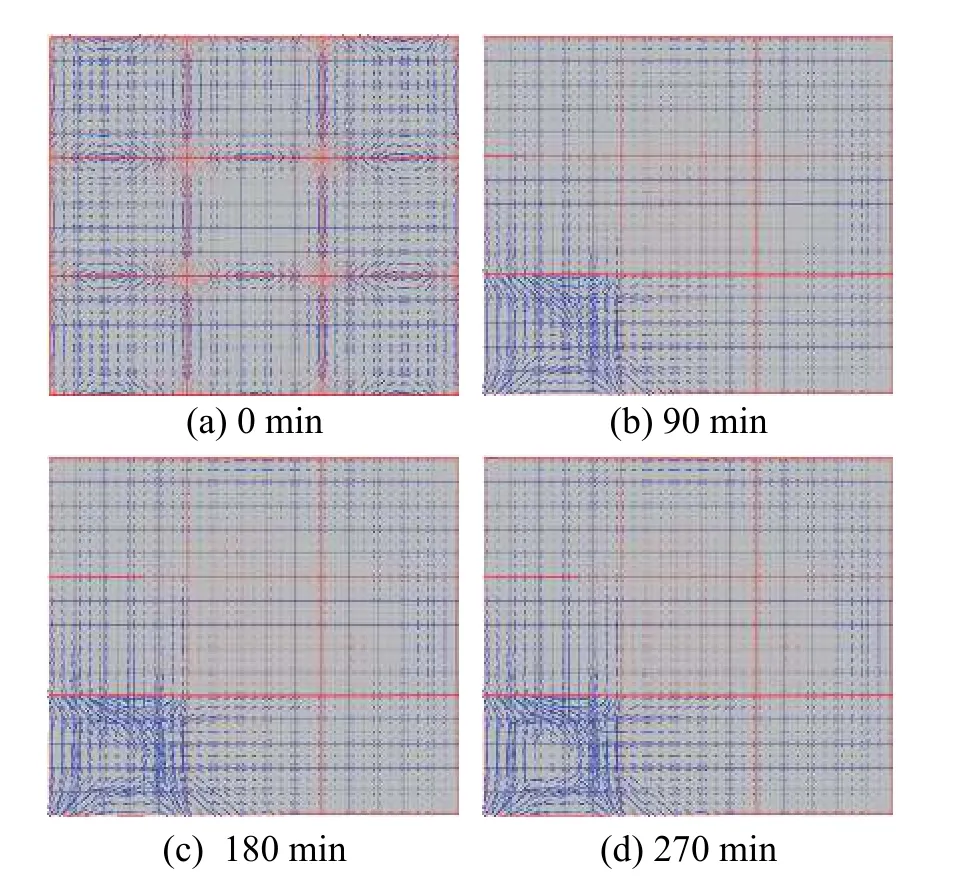
图 9 试验I楼板不同时刻薄膜效应分布Fig.9 Membrane action distributions of Test I at different time

3.4.1 试验I

图9(a)～图9(d)为不同时刻试验I楼板薄膜效应图。可知，边界条件对受火板格薄膜效应分布有决定性影响，具体见下述。

0 min时，根据各板格薄膜力平均值来看，角区格薄膜压力最大，其次是边区格，中区格薄膜力最小。例如，对于角区格，两方向均以受压薄膜效应为主，且受压薄膜力平均值为−11.5。对于中区格，薄膜效应相对较小，平均值为−0.66；对于边区格，受压薄膜效应主要平行与钢梁方向，而另一方向薄膜效应相对较小。此外，与板格内受压薄膜效应不同，各柱顶附近区域板格以受拉薄膜效应为主，且中柱附近薄膜力相对较大，平均值为65.5，其次是外边柱板格区域，平均薄膜力为61.5，而角柱附近板区域，薄膜力最小，平均值为31.8。

一方面，随着温度升高，受火角区格受压薄膜效应快速增大，特别是角柱和内部钢梁附近位置；同时，该板格中心区域薄膜压力逐渐降低，原因在于较大变形，受拉薄膜效应逐渐增加。例如，90 min(180 min和270 min)时，角区格A中心区域薄膜平均值为−311.5(−120.2和−29.6)。最终，受火角区格形成对角U型薄膜机制。另一方面，对于其他非受火板格，受拉薄膜效应区域有所扩大，如270 min，中区格平均受拉薄膜力为114.3；边区格和角区格以受压薄膜力为主，平均薄膜压力分别为−78.1和−48.2。总之，随着温度升高，薄膜效应发展主要集中于受火角板格，而其余非受火板格拉压薄膜效应机制基本变化较小。

3.4.2 试验II

图10(a)～图10(c)为EC2模型所得中区格受火时楼板不同时刻(90 min、180 min和270 min)薄膜效应分布图。值得指出的是，其0 min薄膜效应图与图9(a)一致，不再给出。

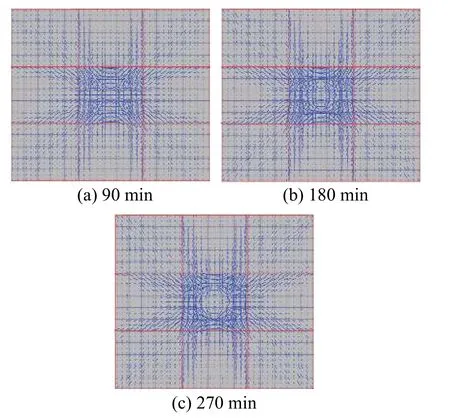
图 10 试验II楼板不同时刻薄膜效应分布Fig.10 Membrane action distributions of Test II at different time

由图10(a)可知，楼板薄膜机理与图9(b)薄膜分布明显不同，进一步表明受火跨位置及其自身边界条件对各板格薄膜效应分布有决定性影响。

一方面，薄膜效应图基本对称，即相同边界条件板格薄膜机理基本相同，且存在三种薄膜分布样式。另一方面，随着温度升高，薄膜样式基本不变，但温度(变形)对薄膜效应值大小和拉压薄膜分布有重要影响。例如，对于中区格，90 min时以受压薄膜效应为主，该板格受压薄膜力变化范围为−31.2～−1634.4，平均值为−430.6；对于四个边区格，靠近受火板格位置，受压薄膜力相对较大(−369.6)，而边缘位置为受拉薄膜力(193.6)，因此该位置出现裂缝(平行内梁方向)；对于四个角区格，45°方向拉压薄膜力较大，其他位置薄膜力较小，进而出现45°方向裂缝(见图7(b))。

与试验I类似(见图9(a)～图9(d))，随着温度升高，薄膜效应分布样式基本维持不变，仅仅相应拉压薄膜效应区域和大小发生变化，特别是受火中区格。如图10(c)所示，由于变形增大，中区格跨中区域受压薄膜力平均值为−349.1，而其边缘薄膜压力值为−858.6。

3.4.3 试验III

图11(a)～图11(d)为EC2模型所得第二层楼板不同时刻薄膜效应分布图。值得指出的是，该四区格内部钢梁受火，而内部柱未受火。可见薄膜效应分布基本沿45°对角线对称分布(见图11(d))。

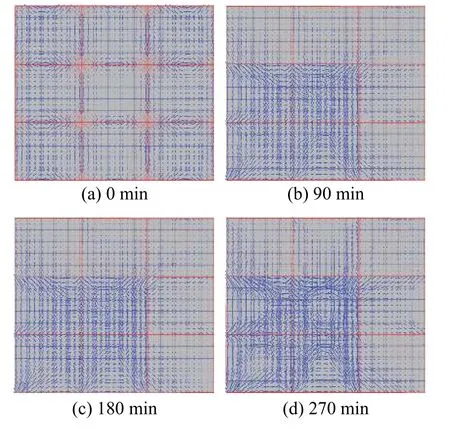
图 11 试验III楼板不同时刻薄膜效应分布Fig.11 Membrane action distributions of Test III at different time

图11(a)薄膜效应分布样式和数值基本与图9(a)相同，可见柱轴力对楼板薄膜效应影响可忽略。一方面，由图11(b)～图11(d)可知，对于受火跨，存在三种薄膜效应分布样式(见图11(c))，即对角U型(角区格)、对边U型(边区格)和环形(中区格)。值得指出的是，90 min(180 min和270 min)时，中区格、边区格和角区格跨中区域平均薄膜压力为−354.1(−233.1和−190.5)、−448.2(−270.6和−222.7)和−210.7(−172.2和−110.9)。可见，板中受拉薄膜效应尚不明显。

另一方面，对于非受火板格，两个边区格薄膜分布基本类似，而三个角区格薄膜分布存在较大差别。此外，值得指出的是，非受火板格钢梁板顶附近区域存在受拉薄膜效应，进而该位置出现沿梁跨方向裂缝(见图7(c))。

3.4.4 对比分析

由上可知，受火板格位置和数量对整体结构中楼板各板格薄膜效应分布有显著影响。一方面，对于受火板格，其薄膜机理主要取决于自身边界条件，进而包括三种薄膜机理，即环型薄膜效应(中区格)、对角U型薄膜效应(角区格)和对边U型薄膜效应(边区格)。

对于受火角板格(见图9)，其两外边(垂直边梁方向)无法提供较强的面内和转动约束作用，该板格拉压薄膜效应需要自相平衡，进而受压薄膜效应(垂直边梁方向)较弱，而平行边梁方向受压薄膜效应较强；对于该角板格两内边区域，周围未升温结构提供较强约束作用，该位置受压薄膜力(双向)相对较大，且受拉薄膜效应相对较大，进而主裂缝出现在该区域[12]。

对于受火中区格(见图10)，周围未升温结构提供较强面内和转动约束，且各方向不能自由膨胀，进而该板格边缘出现较强双向薄膜压力；随着变形增加，该板格中心区域逐渐出现受拉薄膜效应。对于受火边区格(见图11)，其仅一边受面内约束作用较弱，进而该区域出现平行外边缘受压薄膜力；而其余三边约束作用较强，表现为双向受压薄膜效应。

总之，一方面，在火灾下楼板承载力或耐火极限分析时，应考虑边界条件影响，而不能仅仅采用简支板(环型)薄膜效应机制[25]。另一方面，对于非受火板格，其具体分布样式明显取决于受火跨位置和数量，薄膜效应值总体较小，但会引起混凝土开裂，且表现为不同裂缝分布。值得指出的是，若此时结构发生火灾蔓延，上述裂缝会对结构抗火性能有重要影响，特别是隔热性和完整性方面[9−10]，这一点有待深入研究。

3.5 钢梁内力

3.5.1 跨中轴力

图12(a)～图12(c)为试验I、II和III中钢梁轴力-时间关系计算曲线。可知，钢梁轴力随时间逐渐增大，后期曲线较为平缓(平台)。主要原因在于楼板受热膨胀，钢梁产生轴向变形，但其受到柱约束作用，致使梁轴力逐渐增大；随着温度增加，混凝土材料劣化和板跨中出现较大竖向变形，进而膨胀作用减弱，钢梁轴力发展缓慢而出现平台。相比受火跨区域钢梁，非受火区域远端位置钢梁轴力相对较小，基本可以忽略。

例如，试验I中非受火钢梁L1和L2峰值轴力分别为1172.3 kN和917.9 kN，而其余钢梁轴力很小，且火灾过程中轴力基本不变。试验II梁L4峰值轴力最大，其为925.9 kN，而L3、L5和L11峰值轴力相对较小，其分别为98.7 kN、115.1 kN和60.9 kN(平均值为91.6 kN)。

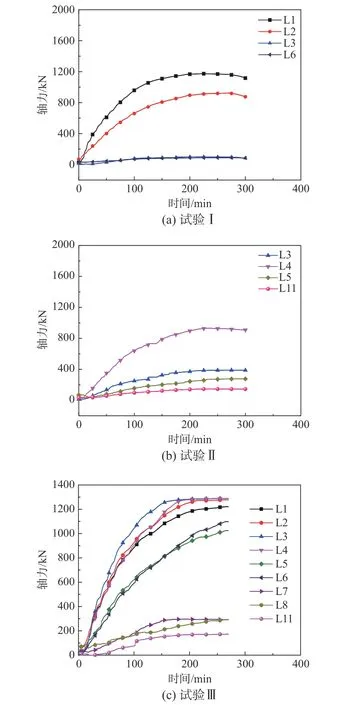
图 12 试验I～试验III钢梁轴力-时间关系曲线Fig.12 Beam axial force-time curve of Tests I, II, and III

对于试验III，与上述两试验类似，试验III中受火板格内部和周边钢梁峰值轴力早期逐渐增大后期逐渐平缓，平缓阶段出现时间为161 min～270 min；停火时，L1、L2、L3、L4、L5和L6峰值轴力分别为1219.9 kN、1276.6 kN、1287.1 kN、1289.7 kN、1023.1 kN和1096.6 kN。四板格同时受火，钢梁峰值轴力明显高于前两个试验受火板格钢梁轴力，相比试验I梁L4，轴力峰值增幅达363.8 kN。对于非受火跨钢梁轴力明显较小，梁L8峰值轴力为293.4 kN。

总之，由于钢梁膨胀作用受到周围构件约束，进而钢梁产生较大轴力，即出现反拱行为，其有助于降低钢梁变形(见图8(a)～图8(d))和提高其抗火性能(见图4(d))。不容置疑，上述力学行为可能导致火灾下钢梁出现过早屈曲破坏，特别是节点位置。因此，近年来，文献[26]提出新的梁柱节点样式，可大大降低升温阶段峰值轴力(即拱效应)，然而，这一点有必要开展深入研究，是否能够在各火灾阶段(升温、降温及灾后阶段等)提高钢梁在结构中抗火性能。另外，在结构中特别关键位置，对节点连接方式进行抗火性能优化设计，进而发挥不同节点在结构整体抗火性能方面(稳定性和结构倒塌)有利作用。

对于试验I和II，边梁L1和中梁L4达到峰值轴力时刻分别约为200 min和210 min，两者峰值出现时刻基本相近；对于试验III，边梁和中梁轴力一直增加，直至试验结束；可见火灾工况对结构中钢梁峰值轴力发展有重要影响。值得指出的是，这一行为与文献[27]对火灾下混凝土框架梁轴力分析结果较为一致。

由上可知，对于结构中钢梁，需要进行大量火灾工况分析(包括火灾蔓延工况)，才可确定其最不利火灾工况。值得指出的是，对于传统结构设计方法，通过忽略约束作用进行构件承载力设计；然而，对于火灾工况下，忽略热膨胀行为和约束作用，基于传统方法或单个构件火灾试验结果，可能过高或过低估计其在结构中抗火性能，有必要采用性能化设计方法[22]。

3.5.2 梁端弯矩

图13(a)～图13(c)为受火钢梁梁端弯矩随时间变化情况。其中，L1-D和L1-U代表L1钢梁的下端和上端；L2-L和L2-R代表L2钢梁的左端和右端。由图可知，梁端弯矩均先增大至峰值，随后逐渐趋于平缓。

对于试验I，停火时，钢梁L1上(下)端和L2钢梁左(右)端弯矩达到峰值176.2 kN·m(−113.6 kN·m)和56.4 kN·m(−125.3 kN·m)，其他钢梁梁端弯矩相对较小。对于试验II，停火时，周边钢梁L4上(下)段和L6左(右)端弯矩分别为−118.8 kN·m(118.8 kN·m)和−116.3 kN·m(116.3 kN·m)，其余钢梁梁端弯矩较小。

图 13 试验I～试验III钢梁梁端弯矩-时间关系曲线Fig.13 Beam-end moment-time curve of Tests I, II, and III

对于试验III，停火时，受火钢梁L2左(右)端和L4上(下)端弯矩分别为88.5 kN·m(−229.8 kN·m)和150.5 kN·m(−205.4 kN·m)。此外，钢梁L1和L3上(下)端分别为−99.8 kN·m(220.3 kN·m)和184.4 kN·m(−210.7 kN·m)；钢梁L5左(右)端分别为61.1 kN·m(−170.1 kN·m)。其他远端钢梁弯矩相对较小。明显地，受火钢梁两梁端弯矩存在较大差别。

3.5.3 跨中弯矩

图14(a)～图14(c)为试验I、II和III钢梁跨中弯矩-时间计算曲线，即为钢梁跨中单元节点弯矩值。由图可知，一方面，受火跨板格钢梁弯矩相对较大，非受火板格钢梁弯矩相对较小。另一方面，对称位置钢梁跨中弯矩基本呈现对称分布，且随着温度升高，跨中弯矩值逐渐增大，但后期增速明显变缓，接近水平。明显地，这一点与文献[28]所得结论(弯矩先增大后减小)略有不同。

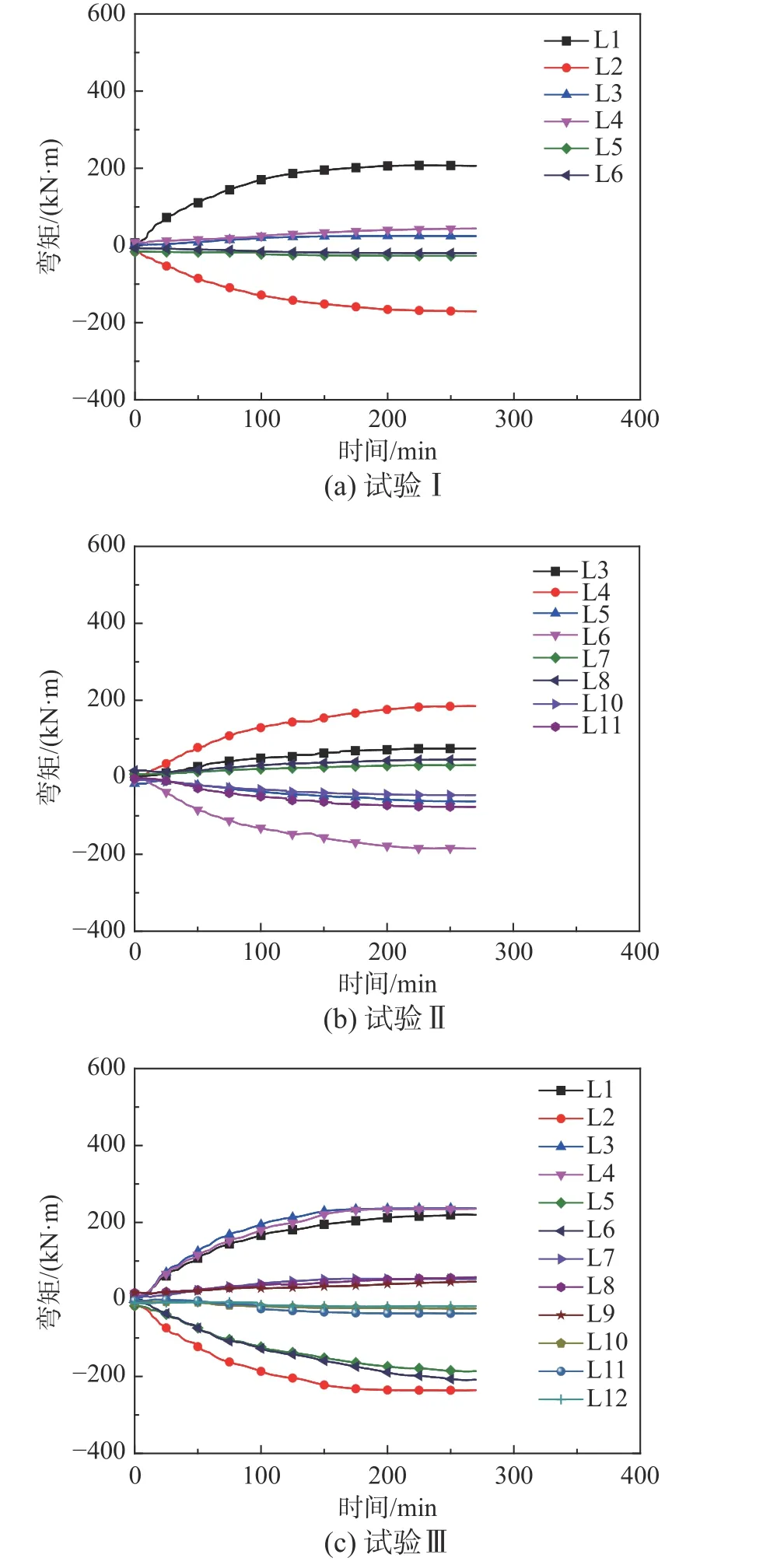
图 14 试验I～试验III钢梁跨中弯矩-时间关系曲线Fig.14 Beam moment-time curve of Tests I, II, and III

上述发展趋势原因在于早期阶段钢梁升温膨胀，但其受到周围未升温结构约束而产生较大轴力，且截面存在温度梯度，产生附加弯矩，即弯矩逐渐增加；后期阶段截面温度一致，且强度和刚度损伤比膨胀作用影响更为显著，跨中弯矩不再增加。值得指出的是，由于杆单元模型局限性，不能有效模拟钢梁局部屈曲或反映节点性能等[29−30]，这一点有待深入研究。

对于试验I，停火时，板格A两未受火梁L1和L2，跨中最大弯矩分别为207.6 kN·m和−169.6 kN·m，明显大于其他梁跨中弯矩，例如钢梁L3(24.6 kN·m)和L5(27.1 kN·m)。同样，试验II和试验III也存在类似规律，即受火板格钢梁弯矩相对较大，例如受火梁L4相应峰值弯矩分别为185.2 kN·m和237.3 kN·m；相比受火跨板格钢梁，非受火跨板格附近钢梁弯矩相对较小，试验III梁L8最大值约为58.2 kN·m。对比常温状态，可见钢梁弯矩增加幅度约为14.3倍。