UHPC-NC叠层梁界面黏结性能的试验研究与数值模拟

许建明，陈 勇，刘骁繁，许 奇

(国网江苏省电力有限公司建设分公司，江苏 南京 210036)

0 引 言

超高性能混凝土材料(Ultra-high Performance Concrete，UHPC)由于其优异的材料强度、延性与耐久性表现，在土木工程领域得到了广泛的研究[1-4]。目前，UHPC材料的工程应用主要局限在既有结构的维修加固[5-7]与结构局部构造的快速施工[8-9]。这主要是因为当前UHPC材料的成本高昂，且制备与养护条件要求较高。为了更加经济、高效地利用UHPC优异的材料性质，将其与普通混凝土(Normal Concrete，NC)形成组合构件的想法应运而生。

UHPC与NC两种材料在弹性模量、收缩徐变、热膨胀等物理性质上均存在明显的差别。因此，在外部荷载作用下，两者之间的界面会发现黏结失效，从而影响构件的服役能力[10]。与NC-NC界面相比，UHPC与NC之间展现出更好的黏结性能[11]。目前有多种试验方法用以评估2种材料间的黏结强度：推出试验与直拉试验可以用于Ⅰ型破坏强度；直剪试验与斜剪试验则可以体现Ⅱ型破坏强度[12]。

对于UHPC-NC组合构件，目前已有学者进行了试验研究。Habel等[13]对12个利用UHPC加固的梁构件进行了弯曲试验，发现UHPC优异的材料特性能显著改善加固后构件的结构响应。Al-Osta等[14]研究了利用UHPC材料的不同加固方式，其研究发现采用UHPC三面U型加固试验梁加固效果最为显著。王春生等[7]、孔小芳[15]、刘超等[16]也对利用UHPC加固的梁构件进行了试验研究。

相较于试验研究，UHPC-NC叠层梁的数值模拟研究尚未得到完美的解决。Sadouki等[17]利用弥散裂缝的方法在DIANA软件中模拟了Noshiravani等[18]进行的UHPC-NC悬臂梁试验，但是其研究并没有体现出界面黏结的作用，该有限元模型是基于2种材料间完美黏结的假设。Al-Osta等[14]和Safdar等[19]的模拟研究也是采用了界面完美黏结的假设，这可能会导致模拟所得的UHPC-NC构件承载能力偏高。Lampropoulos等[6]则采用ATENA软件模拟界面对UHPC-NC构件行为的影响，其假设界面的摩擦因数为1.5，黏结强度为1.9 MPa，然而这一假设并没有试验数据佐证。这些数值模拟离UHPC-NC叠层构件的真实受力行为还有明显差距。

为了更好地模拟UHPC-NC的受力行为，本文采用非局部的方法来模拟UHPC与NC层，通过合并高阶变形量形成梯度损伤模型[20]。这种梯度损伤模型可以模拟损伤的产生与发展，且具有更稳定的显性算法。对于2种材料之间的界面，本文将不再采用完美黏结假设，充分考虑界面的黏结破坏以及其对UHPC-NC组合构件受力行为的影响。

1 叠层梁静载试验

1.1 叠层梁试件

为了研究UHPC-NC叠层梁中界面黏结强度对受力行为的影响，本研究浇筑了3个UHPC-NC叠层梁试件UN50，UN60，UN70，其矩形横截面宽250 mm，高150 mm；试件全长1 200 mm，加载净跨径为1 000 mm。试件UN50，UN60，UN70的下层UHPC厚度分别为50，60，70 mm，如表1所示。

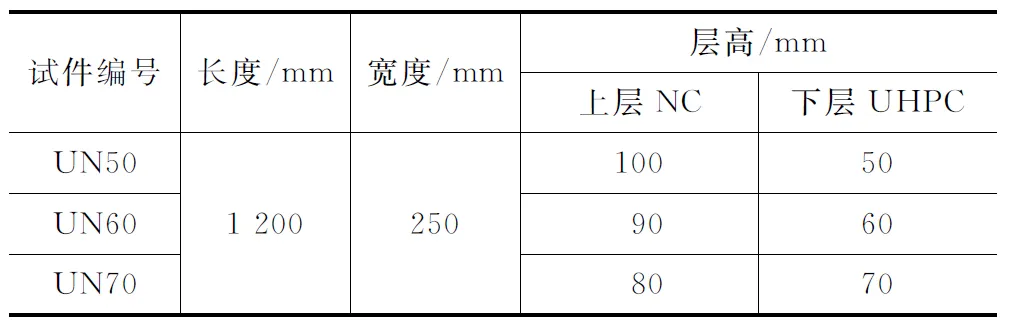
表1 试件的尺寸Tab.1 Dimensions Details of Specimens

UHPC-NC叠层试件示意如图1所示。为了更好地体现界面黏结性能对UHPC-NC叠层梁力学行为的影响，本研究浇筑的3个试件中均没有布置任何抗弯钢筋在UHPC或NC层中，也没有布置任何钢筋穿过试件的界面。所有的试件均采用分次浇筑的方式。首先，浇筑下层UHPC并自然养护28 d，养护期间使用防雨布覆盖并定期进行湿润处理。为了保证界面拥有足够的黏结强度，在浇筑表层NC之前将UHPC底层浸泡在水中超过10 h。值得一提的是，本研究中的UHPC-NC界面为自然表面，没有采用任何人工表面处理措施。

所有试件在浇筑完成后均采用力控制的四点弯曲加载方式(图2)，试验所采用的液压加载装置能够准确控制其施加的荷载与行程。除了采用传统的位移计监测试件的跨中挠度外，本试验还采用数字图像相关技术(Digital Image Correlation，DIC)记录加载过程中试件的裂缝发展与应变场变化。

1.2 改进的斜剪试验

对于2种材料间界面的黏结强度，目前已有多种试验方法进行测量确定，例如：直拉试验、推出试验、劈裂试验和斜剪试验等。斜剪试验能够体现界面同时受正应力与剪应力作用的真实服役状态，因此可以更准确地评估UHPC-NC之间的界面抗剪强度[21]。

本研究共浇筑了9个界面斜剪试件，采用与上述叠层梁同批次的UHPC与NC材料，界面处理方式也与叠层梁的界面完全一致。所有斜剪试件总高度均为400 mm，界面的水平角度分为50°，60°和70°三组。试验采用1 000 kN级电液伺服加载装置进行位移控制加载。

在常规的斜剪试验中，通常会出现NC局部受压破坏而非界面破坏的现象[10,22]。因此，本研究对常规斜剪试验进行了改进(图3)。本文中斜剪试件的下半部分截面尺寸(150 mm×100 mm)大于上半部分截面尺寸(100 mm×100 mm)，并且NC部分采用FRP布进行了包裹加固。这2个措施都是为了使试件在加载过程中避免发生NC局部受压破坏，确保最终破坏发生在界面处，从而较为准确地获得本研究的UHPC-NC界面抗剪强度。

2 模型所采用的本构关系

2.1 UHPC与NC所采用的局部损伤梯度模型

(1)

式中：ε为应变；E为四阶弹性张量；h为耦合模量；c为梯度参数；g为一个交换方程；为那勃勒算子；Ω为积分区域。

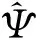
(2)

根据Coleman-Noll理论，可得其本构关系为

(3)

(4)

(5)

(6)

基于上述公式，可以获得以下局部损伤梯度模型的控制方程

(7)

(8)

式中：b为构件的内力。

(9)

如上所述，局部损伤梯度模型假设区域的失效发展区域随着累积损伤因子d的增长而减小。因此，交互函数g(d)满足g(0)=1且g(1)→0，为

(10)

式中：R和n均为材料参数。

根据修正Von Mises理论[25]可得等效应变标量εeq为

(11)

式中：ν为泊松比；k为材料抗压强度fc与抗拉强度ft的比值；I1为应变张量的第一不变量；J2为偏应变张量的第二不变量。

损伤参数采用损伤因子d的指数形式进行表达，从而体现出最大荷载后较长的软化阶段，即

(12)

式中：κ为不可逆的损伤因子；κ0为损伤阈值；γ为材料完全损伤后的剩余强度；β为软化阶段的斜率参数。

κ可以定义为非局部等效应变的最大值，即

(13)

局部损伤梯度模型的优点就在于能够识别出：①最大荷载前微裂缝的形成；②随着加载过程的微裂缝发展；③最终微裂缝聚集形成宏观裂缝。从而实现对准脆性材料损伤的数值模拟[23]。

2.2 考虑黏结与摩擦的界面模型本构

根据Xu等[26]的研究，界面的破坏作用力向量T=(Tn，Tt+Tf)T(Tn和Tt分别为界面法向与切向的作用力，Tf为切向摩擦作用力)可以由界面的开裂势能φ对位移向量Δ=(Δn，Δt)T(Δn和Δt分别为法向与切向变形)求导所得

(14)

对式(14)进行正则化[27]可得

(15)

(16)

式中：σmax为无切向位移下的最大法向应力；τmax为无法向位移下的最大切向应力；δn，δt分别为法向和切向位移；ξn和ξt分别为描述界面损伤过程中法向与切向耗能的参数。

界面单元的法向与切向应力-应变关系如图4所示。

(17)

式中：φn和φt分别为界面的法向与切向的损伤势能。

(18)

(19)

式中：Δn,max和Δt,max分别为加载过程中界面在法向和切向的最大变形。

当界面法向变形量为0(Δn=0)时，界面发生接触作用，法向作用力可表达为

(20)

式中：α为惩罚因子，其数值可取10，从而同时保证模型预测的准确性与计算过程的稳定性[29]。

界面的法向与切向应力在往复加载过程中的发展规律如图5所示。

界面的胶结与摩擦耦合作用如图6所示[30]，界面可以划分为未损伤区Au和损伤区Ad，即

(21)

式中：D为损伤参数。

UHPC-NC界面研究假设在未损伤区Au仅存在胶结力作用，而在损伤区Ad则存在摩擦力作用。因此，界面的切向作用力由胶结力Tt(Δn,Δt)和摩擦力Tf(Δn,Δt)两部分组成，即

(22)

(23)

式中：Et为界面切向初始刚度；μ为摩擦因数。

损伤参数D则取决于界面法向与切向的变形Δn和Δt。损伤参数D(Δn,Δt)可由下式计算

(24)

公式(22)，(23)中的参数Et为Δn=0时的界面切向初始刚度

(25)

综上所述，公式(14)中包含黏结力和摩擦力作用的界面作用力向量为

(26)

3 有限元模型建立

3.1 材料参数的选取

表2 NC与UHPC的材料性质Tab.2 Material Properties for NC and UHPC

本研究所采用的UHPC为商业产品，其每立方米的配合比为：2 095 kg的细骨料、156 kg的钢纤维(占体积的2%)、22.1 kg的外加剂和182.4 kg的水。通过9个UHPC立方体试件(100 mm×100 mm×100 mm)试验，测得其28 d立方体抗压强度为129.7 MPa。根据3个尺寸为100 mm×100 mm×300 mm的棱柱体试验，测得UHPC的弹性模量 为55.5 GPa。另外，本试验还浇筑了2个总长500 mm、中间矩形截面为100 mm×50 mm的骨棒形试件以测量UHPC材料的抗拉强度，其试验应力-应变曲线如图7所示。

3.2 UHPC-NC界面斜剪试验

本研究改进了现有的标准界面斜剪试验，扩大基座的截面尺寸并用FRP布包裹加固NC部分。这些优化措施能够确保构件在加载试验中破坏发生在界面而非NC局部。试验中测得的界面抗剪强度τtest为

(27)

式中：P为极限荷载；A0为垂直于荷载的接触面投影面积，本研究中A0=100 mm×100 mm。

本研究进行的界面斜剪试验结果如表3所示。斜剪试验所测结果τtest可以利用第2.2节所述的有限元模型进行验证，其拟合所得的界面黏结力为1.04 MPa，摩擦因数μ为1.60。对于破坏势能，本文采用Shah等(2010)对于NC-NC界面的研究成果，取φn=φt=50 m-1。图8为斜剪试验的有限元模型验证。

表3 斜剪强度测试结果Tab.3 Results of Slant Shear Strength Test

3.3 基于ABAQUS的随机有限元模型

以试件UN60为例，本文所建的有限元模型如图9所示，该模型为二维平面模型，单元网格尺寸为10 mm×10 mm。UHPC和NC材料采用8节点矩形单元来模拟，而界面则采用零厚度的6节点单元来模拟。单元的本构关系如第2节中所述，采用UEL子程序在通用有限元软件ABAQUS中实现分析计算。

混凝土材料本质上是各组分组成的各向异性材料。因此，对于本研究中的无配筋混凝土梁试件，有必要考虑材料性质随机分布对其受力行为的影响。因此，采用随机有限元理论能够更加准确地模拟UHPC-NC叠层梁的加载破坏过程。根据已有研究成果[31-32]，威布尔分布能够有效描述混凝土中的累积开裂概率Pf

(28)

式中：m为威布尔分布系数；σu为特征强度；σw为失效概率接近0时对应的威布尔应力；参数m和σu均由材料自身性质所决定，其中参数m数值越大代表材料参数的性质越趋向于各向同性。

4 试验结果与有限元结果对比

4.1 试件UN50

试件UN50呈现出典型的弯曲破坏，在2个加载点之间的纯弯区域出现了1条贯穿两层的竖直主裂缝(图11)。在该试件中，没有观测到UHPC-NC界面出现任何裂缝或脱落。由于试件中没有布置任何钢筋，试件在70.7 kN荷载作用下发生较为脆性的破坏。

本研究建立的3个基于威布尔分布的随机有限元模型所得到的最大荷载损伤情况如图12(a)所示。与试验观测结果相同，数值模拟结果的主要损伤为弯曲裂缝，且没有出现任何界面的失效。有限元模型所得的荷载-跨中挠度曲线与试验实测结果的比较如图12(b)所示。由图12(b)可以看出，有限元模型所得的试件刚度与极限承载能力均与实测结果接近。所建立的3个有限元模型的最大承载力分别为70.2，69.3，71.2kN，与实测值70.7kN接近。

对于UHPC-NC界面的应力水平，选取2个典型加载状态进行展示：跨中挠度为1 mm时，试件尚处于弹性阶段；施加极限荷载时，能够体现出试件的最不利状态。试件UN50的界面法向与切向应力如图13，14所示。模拟结果表明，尽管界面的切向应力随着荷载不断增加，但始终低于胶结强度。类似地，在跨中挠度为1 mm时仅在支座与加载点附近存在明显的法向界面应力。随着荷载的增加，混凝土发生开裂，试件在纯弯段也出现界面法向应力，但其数值也小于胶结强度。因此，该试件的界面在加载过程中能够保持完好无损。

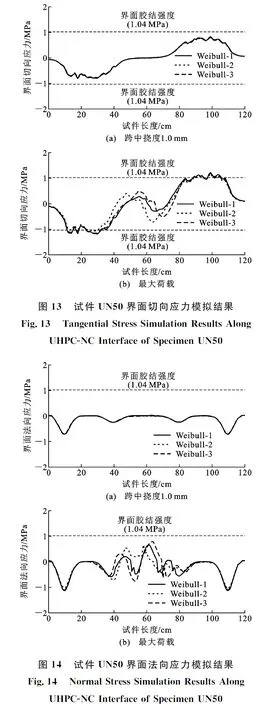
借助于DIC技术，本研究记录了加载过程中肉眼难以观测的裂缝发展过程。当施加的荷载为63.8 kN时，UHPC底层开始出现弯曲微裂缝；荷载达到67.0 kN时，上层NC开始开裂，此时UHPC底层的裂缝已经相对稳定；当荷载增加到68.2 kN时，上下层的裂缝交汇，产生贯穿试件的受弯主裂缝。图15给出了模型Weibull-1模拟结果与DIC记录结果的对比。可以看出，有限元模型的损伤发展过程与试验现象较吻合。

4.2 试件UN60

不同于试件UN50，试件UN60虽然在UHPC下层出现弯曲裂缝，但是最终的弯曲断裂仅发生在上层NC中，且从NC弯曲裂缝到梁端的UHPC-NC界面出现失效脱落(图16)。

图17(a)给出了UN60的有限元模拟损伤示意图。在最大荷载作用下，UHPC底层中存在弯曲裂缝但未发展到上层NC中，最终的破坏断裂发生在上层NC中。这些现象均与试验观察到的一致。由图17(b)所示的荷载-跨中挠度曲线可以看出，该有限元模拟得到的试件刚度与试验结果较吻合。3个有限元模型得到的最大承载能力分别为72.1，71.9，72.5 kN，均与实测的76.9 kN接近。

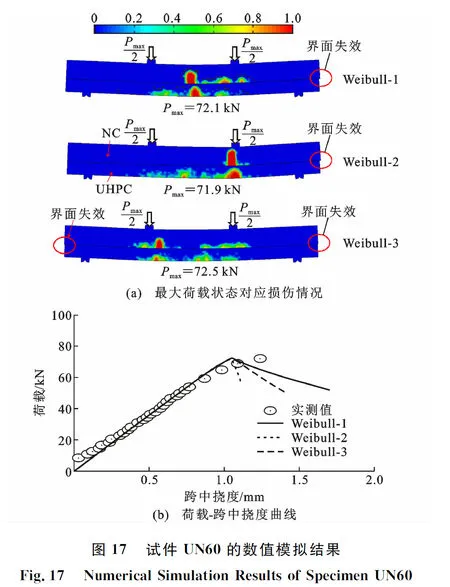
如图18所示，对于所建立的模型Weibull-1和Weibull-2，在最大荷载作用下，400～1 200 mm长度范围内的界面切向胶结力失效，存在摩擦力作用在界面现象，表现在右侧的上层NC失效脱落。另一个模型Weibull-3则在试件的左右两侧均界面失效。试件UN60的法向界面应力有限元分析结果如图19所示，可以看出混凝土的开裂与裂缝发展会对界面的法向应力分布情况产生显著影响。

根据DIC的记录结果，UHPC下层在荷载为72.0 kN时出现了第一条弯曲裂缝，此时上层NC还保持完好。当外荷载达到74.0 kN时，上层NC中开始出现弯曲裂缝。随后，当外荷载达到76.9 kN时，上层NC中的裂缝贯穿。如图20所示，有限元模型Weibull-2的损伤发展过程与试验观测结果较为接近。

4.3 试件UN70

与其他2个试件明显不同，随着下层UHPC厚度的继续增加，试件UN70最终呈现出上层NC的斜剪破坏，并伴随有界面的失效与脱落(图21)。根据3个随机有限元模型得到的极限荷载分别为107.2，106.7，104.5 kN，与试验测得的100.5 kN较为接近。

试件UN70的模拟结果如图22～24所示，损伤发展过程如图25所示。由此可见，模拟结果与观测到的试验现象相一致。有限元的界面切向应力分析结果显示，试件的右侧会出现界面胶结力失效并脱落的现象。在发生最终破坏时，跨中纯弯段也有明显的界面切向应力存在。

DIC的记录显示，在84.1 kN的外荷载作用下，下层UHPC出现了初始弯曲裂缝；当外荷载增加至91.5 kN时，上层NC出现斜剪裂缝；当荷载到达100.0 kN时，界面黏结失效并沿斜剪裂缝脱落。有限元模型Weibull-1的损伤演化过程与试验观测接近。

5 结 语

(1)对UHPC-NC叠层梁的受力结构特性进行了试验研究。试验所浇筑的3个不同厚度比的UHPC-NC叠层梁试件呈现出不同的破坏模式，说明界面的黏结性能对叠层梁的受力行为表现具有显著影响。此外，本研究还改进了现有的界面斜剪试验，以获得更加准确的UHPC-NC界面性能。

(2)构造了UHPC-NC叠层梁的有限元模型，集成了UHPC和NC的局部损伤梯度模型，耦合了胶结与摩擦作用的界面模型。通过考虑材料性能的威布尔分布，以使有限元模拟结果更加真实可靠。结果表明，有限元模型可以较好地体现UHPC-NC叠层梁的真实受力行为。此外，有限元模型的分析计算结果还体现了界面法向与切向应力的变化，为相关的界面行为研究提供了一定的见解。研究表明，UHPC-NC的界面强度性能至关重要，并且在某种程度上将决定叠层构件的受力行为。