一种LCL型并网逆变器双闭环参数设计方案
2021-07-24李亚洲孙志伟迟殿委
李亚洲,孙志伟,迟殿委
(山东外事职业大学信息与控制工程学院,山东 威海 264504)
0 引言
随着全球变暖环境问题日益突出,可再生能源如风能、太阳能和水电被视为可靠地替代传统能源(石油、天然气或煤)。基于可再生能源的分布式发电系统DPGSs(Distributed Power Genera-tion Systems)在全球大发展[1-2]。微电网是一种利用可再生能源发电的小型发配电系统[3-6],它既可以实现孤网运行,也可以与大电网并网运行,在并网过程中微电网接入点的电压、线路潮流、线路电流、电能质量、继电保护以及网络可靠性等都将产生影响[7],而并网的目的就在于消除此影响,使微网在并网运行模式下更为安全稳定。通常采用LCL型逆变器作为输出滤波器,与采用L滤波器相比,LCL滤波器是三阶系统,具有更好的高频谐波衰减能力,可实现总电感值更小的条件下,具有相同的滤波效果,在直流逆变电力系统中被广泛应用[8-9]。
LCL滤波器传递函数特征方程中缺少一次项,是不稳定的,若不加以改进或控制不当,会破坏系统稳定性。其传统解决方法是在LCL滤波器的电容支路中串入阻尼电阻,这种无源阻尼方式解决了系统的稳定性问题,但电阻会带来额外的有功功率损耗,从而使系统效率下降[10-13]。针对无源阻尼存在的不足,许多文献提出了有源阻尼方法,有源阻尼是通过增加系统的反馈环节来抑制谐振峰[14-15],但这会增加系统的复杂性和额外的成本。针对电流反馈有源阻尼数字控制下的一拍滞后延时会降低系统稳定裕度,限制并网电流环的环路增益和带宽的提高,文献[16-17]提出了并网电流二重采样法,消除了采样计算引入的一拍滞后,但在一个开关周期内装载两次调制信号,容易产生开关纹波。文献[18]采用电容电流反馈有源阻尼方法,分析PI调节器参数和电容电流反馈系数等闭环参数对并网电流稳态误差、系统相位裕度和幅值裕度的影响,确定满足要求PI调节器参数和电容电流反馈系数,但是仍然需要反复试凑。
本文通过分析 LCL型双闭环并网逆变器模型,建立了LCL型双闭环控制器的空间矢量数学模型;其中内环采用电容电流比例环节,可有效抑制LCL滤波器的谐振峰,外环采用比例积分环节,实现网侧电流控制;依据主导零点、主导极点法理论,提出了3条闭环系统零极点配置原则。以配置原则为依据,讨论了不同开环零极点下根轨迹在 s域左半平面的分布,推导出控制器内外环参数对系统稳定性和动态特性的影响,得出控制器参数的限定范围。最后,结合根轨迹对控制器参数进行寻优,同时利用频率分析法,通过幅相图验证系统的对数频率特性曲线是否满足控制系统要求。仿真实验表明所提出的算法可获得较好的系统稳定性和高频谐波抑制能力。
1 系统拓扑结构及数学模型
单相并网逆变器拓扑结构,如图1所示。其中:L1,L2为滤波器电感;C为滤波器电容;电感L1、电感L2和电容C构成LCL型滤波器。i1为逆变器输出电流,Udc为逆变器直流输入电压;Vi为逆变器输出电压;i2为并网电流;R1为电感L1的内阻以及继电器开关、死区效应、线路损耗等各种阻尼因素产生的逆变器侧等效电阻,R2为网侧等效电阻;VC为电容电压,US为电网电压。
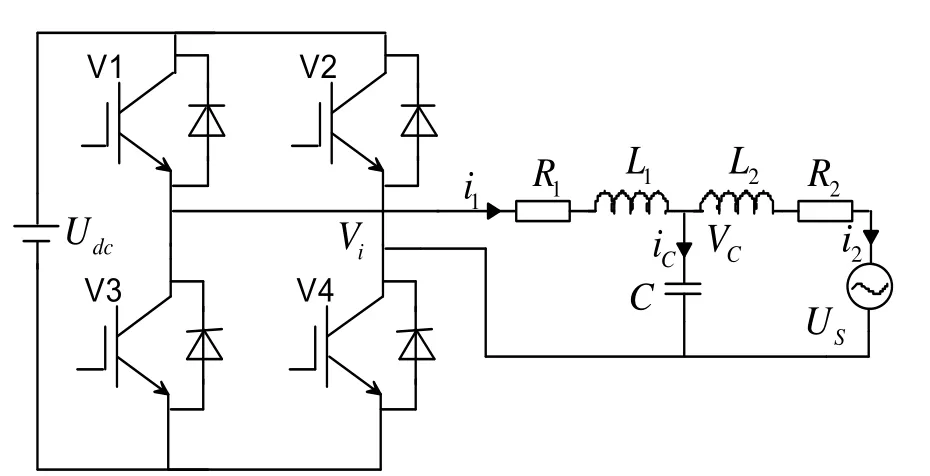
图1 单相并网逆变器拓扑结构Fig.1 Single-phase grid-connected inverter topology
根据图1系统的拓扑机构,图2建立了系统数学模型结构图。
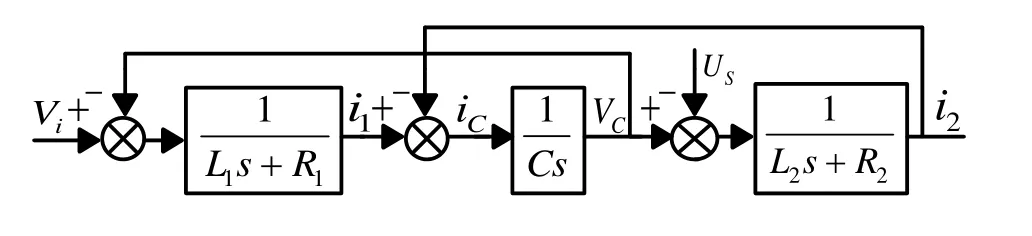
图2 系统数学模型结构图Fig.2 Math ematical model structure diagram of the system
由于电阻R1,R2很小,分析系统模型时可忽略,故由图 2得到并网电流i2的传递函数数学模型,如式(1)所示。
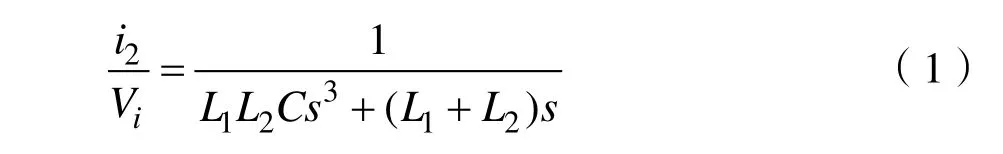
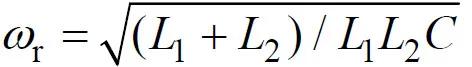
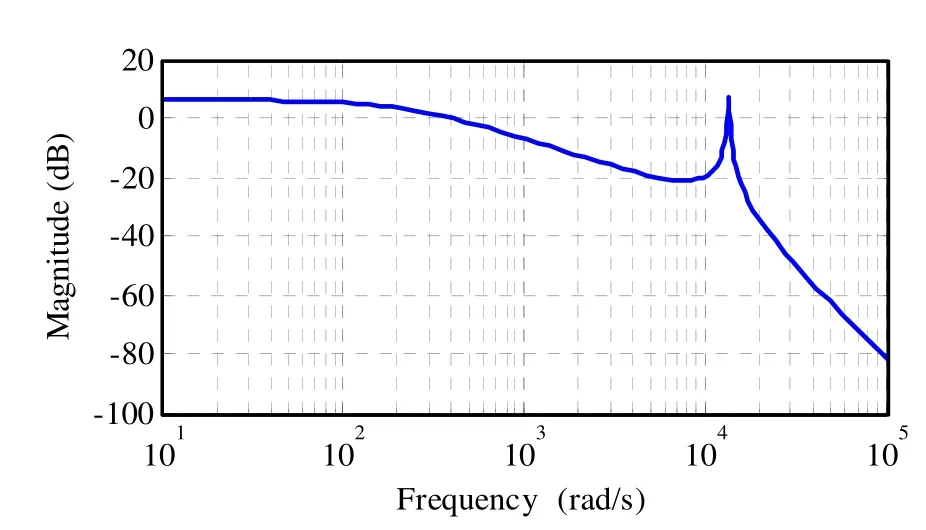
图3 LCL 滤波器Bode图Fig.3 Bode diagram of LCL filter
2 控制器参数设计与优化
2.1 控制器参数的设计
LCL型单相逆变器双电流环系统控制框图如图4所示。内环采用电容电流比例环节、外环采用并网电流PI环节。图中KC为内环电容电流比例系数;KP和KI分别是外环PI控制器的比例系数和积分系数;i2ref为并网指令电流。
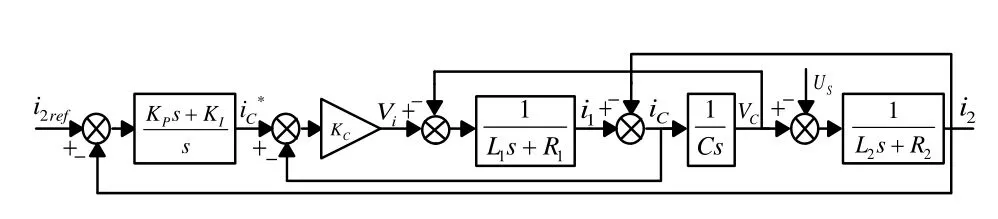
图4 电流双闭环控制系统框图Fig.4 Block diagram of current double closed-loop control system
由图4可得到网侧电流i2,如式(2)所示。
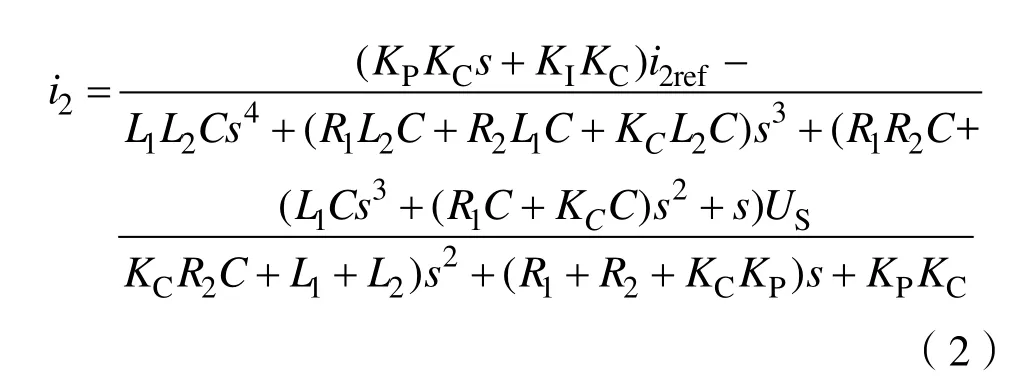
不考虑电网电压US对电网的影响,得到系统开环传递函数,如式(3)所示。
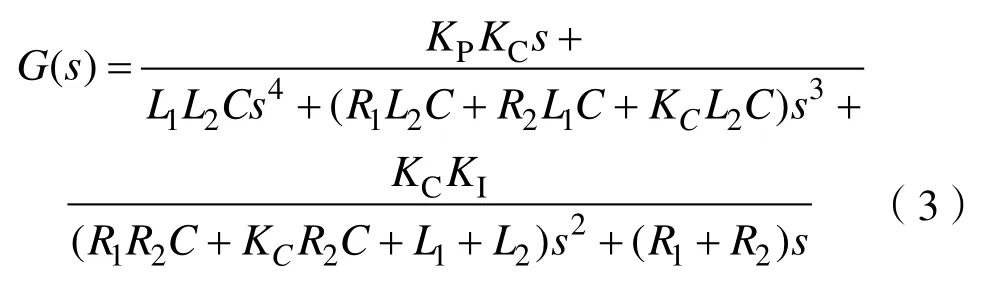
R1、R2很小,分析系统特征时将其忽略,得到系统的开环传递函数,如式(4)所示。
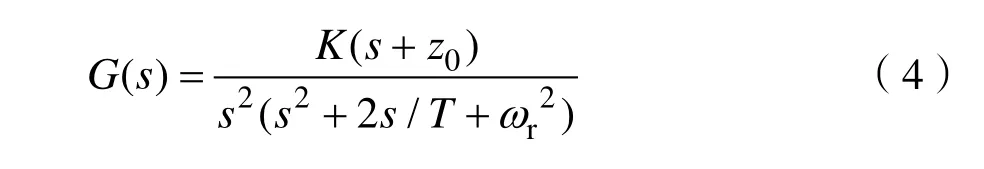
式(4)中:K为根轨迹增益;z0为开环零点;T为开环非主导极点时间常数;rω为LCL滤波器谐振频率。各个参数如式(5)所示。
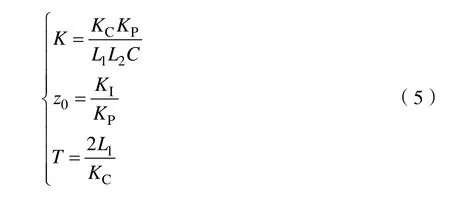
由系统开环传递函数可知,由于z0和T是未知的,故无法画出系统的根轨迹图。本文研究的重点就在于对闭环系统传递函数的零极点进行配置,其配置原则是使闭环系统存在一对互为共轭的主导极点和一对互为共轭的非主导极点。由自控原理[28]可知,在实际工程应用中,闭环主导零、极点距离虚轴较近,对系统的性能影响起主导作用;比主导极点距离虚轴2~3倍的闭环非主导零、极点可放在略去之列。由此可得:一方面应使非主导极点远离虚轴,另一方面应保证附加开环零点改善系统稳定性和提高系统动态特性的作用,故z0不可远离开环主导极点,保持z0对闭环主导极点根轨迹图的吸引力,使其发生向 s域左半平面方向的弯曲。
由以上分析,对闭环系统零、极点及根轨迹做出如下配置原则:
(1)主导极点为接近虚轴的一对共轭复根;
(2)非主导极点为一对共轭复根,且比主导极点距离虚轴2~3倍以上,且非主导极点的根轨迹在s域左半平面的实轴上存在分离点(d,0);
(3)开环零点z0在非主导极点距离虚轴 1/3处,且能吸引主导极点的根轨迹图发生向s域左半平面方向一定程度的弯曲。
由配置原则(2)及根轨迹在实轴的分布可知,随着根轨迹增益K的增大,非主导极点在分离点(d,0)处进入 s域左半平面的实轴,一支趋向于(-z0,0),另一支趋向于无穷远处。故非主导极点共轭复根实部α的限定范围为:

为优化系统的整体性能,可加强非主导极点对系统作用。基于本文的控制器,在不违背原则(2)的思想下,容许非主导极点在一定范围内其进入实轴,本文将在2.2节具体讨论。
假定在最坏的情况下,为满足系统的性能指标,非主导极点随着根轨迹增益K的增大将趋于分离点(d,0)处。由以上配置原则及式(4),可得如下式(7)。
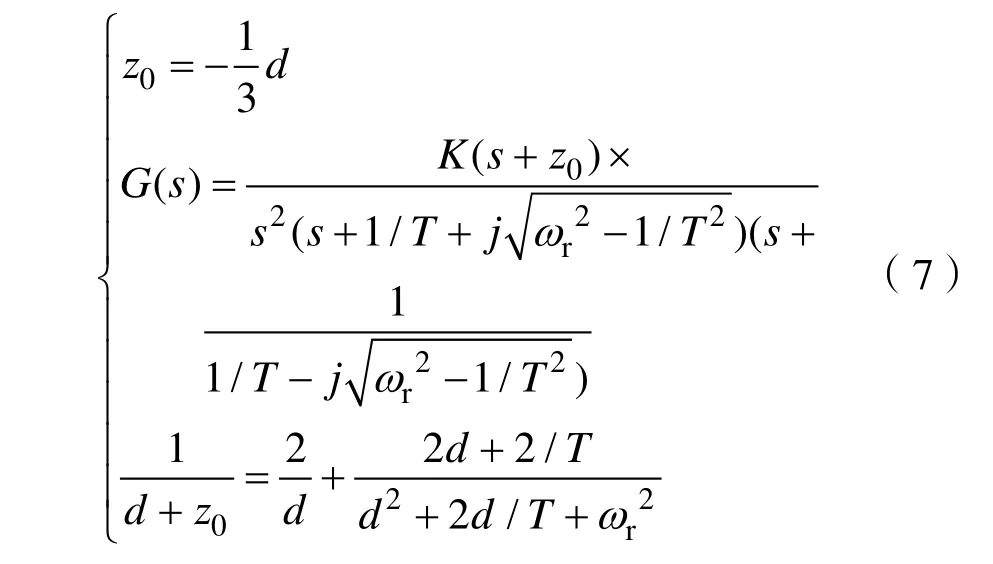
由式(7)及配置原则(2),得到分离点d,如式(8)所示。
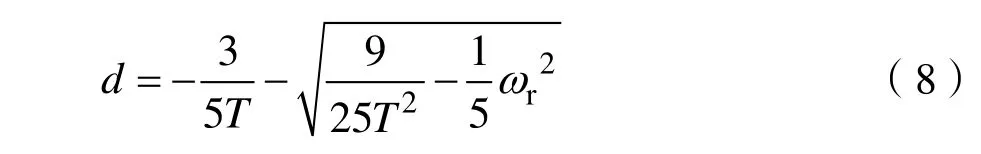
由式(8)可知,1/T越大,分离点d距离虚轴越远,非主导极点对系统的影响越小;但由式6可得,此时零点也将远离虚轴,违背配置原则(3)。故应对参数T合理配置,而式(7)、式(8)中含有1/T的约束条件,由此,可得1/T的限定范围,如式(9)所示。

由式(9)可知,1/T限定在约 0 .75ωr~ωr区间内。为验证配置原则的正确性,选取参数1/T=0.9ωr,由式(7)、式(8)联立得到参数z0=3.8032× 103。由此,画出初步整定参数后闭环系统的根轨迹图,如图5所示。
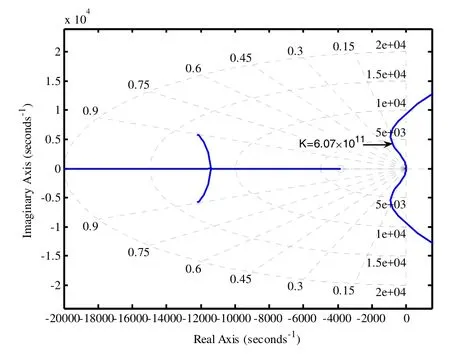
图5 参数初步整定闭环系统根轨迹Fig.5 Root locus of closed-loop system after initial setting parameter
由图 5可知,即使非主导极点的根轨迹越过分离点进入实轴,也将远离虚轴和主导极点的根轨迹图;开环零点在分离点的 1/3处;主导极点的根轨迹接近虚轴。综上所述,验证了系统根轨迹图基本符合上文提出的3条配置原则。然而,从图5中同时可得到,零点虽远离了非主导极点,但距离开环主导极点的距离依然过大,导致主导极点根轨迹图趋向s域左半平面的弯曲程度不足,使得阻尼比ζ过小,系统稳定性下降。在根轨迹增益K= 6 .07× 1 011处,ζ取得最大值0.2,画出闭环系统的Bode图,如图6所示。
由图6可知,LCL谐振峰虽得到一定程度的抑制,但系统的相角裕度γ=22.7°,不足以满足稳定性要求,经此验证,故还需对控制器参数进行优化。
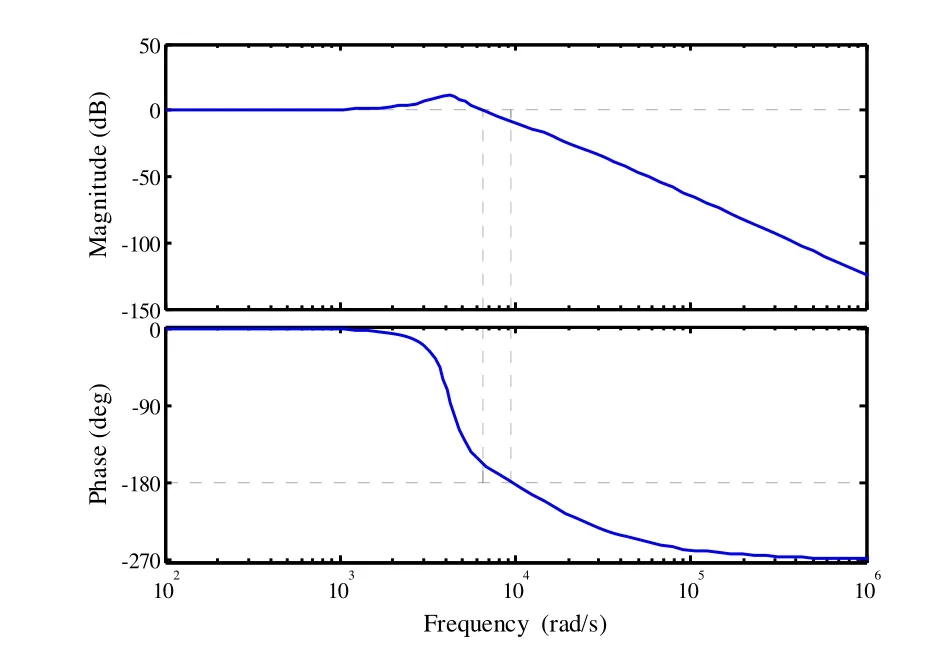
图6 闭环系统Bode图Fig.6 Bode diagram of closed-loop system
2.2 控制器参数的优化
根据上节的分析,需要进一步优化控制器参数T和z0,基于此,本文采用根轨迹对控制器参数T和z0进行寻优,并分析各参数对系统稳态、动态特性的影响,通过幅相图进一步分析系统的对数频率特性曲线,以此验证所优化参数的可行性。
由上节分析可得:在控制器参数z0= 3 803,1/T= 1 .21× 1 04处,由于z0距离开环主导极点太远,违背配置原则(3),造成阻尼比ζ小于0.2,在根轨迹中无法找到满意的闭环系统特征根,故需加强附加闭环零点的作用,使主导极点的根轨迹图进一步趋向 s域左半平面方向弯曲,提高系统的稳定裕度。由此,分别取z0= 3 400,z0=3000,z0= 2 600,得到图7所示,闭环系统的根轨迹图。
会计故意性信息失真是指会计活动当事人(包括国有企事业、非公有制企业、上市公司、中介服务机构)出于各种目的,利用会计规范给会计活动当事人的灵活性,事先经过周密安排而从主观上故意有偏向性或诱导性的提供信息或者违背会计规范,制造假账,而造成的信息失真。[1]会计故意性信息失真分为二类:第一类如银广厦、琼民源的财务报告完全是无中生有、恶意编造,违背社会道德和法律;第二类是利用内外串通,共同操纵、利用信息不对称和财务技能的优势共同作弊。
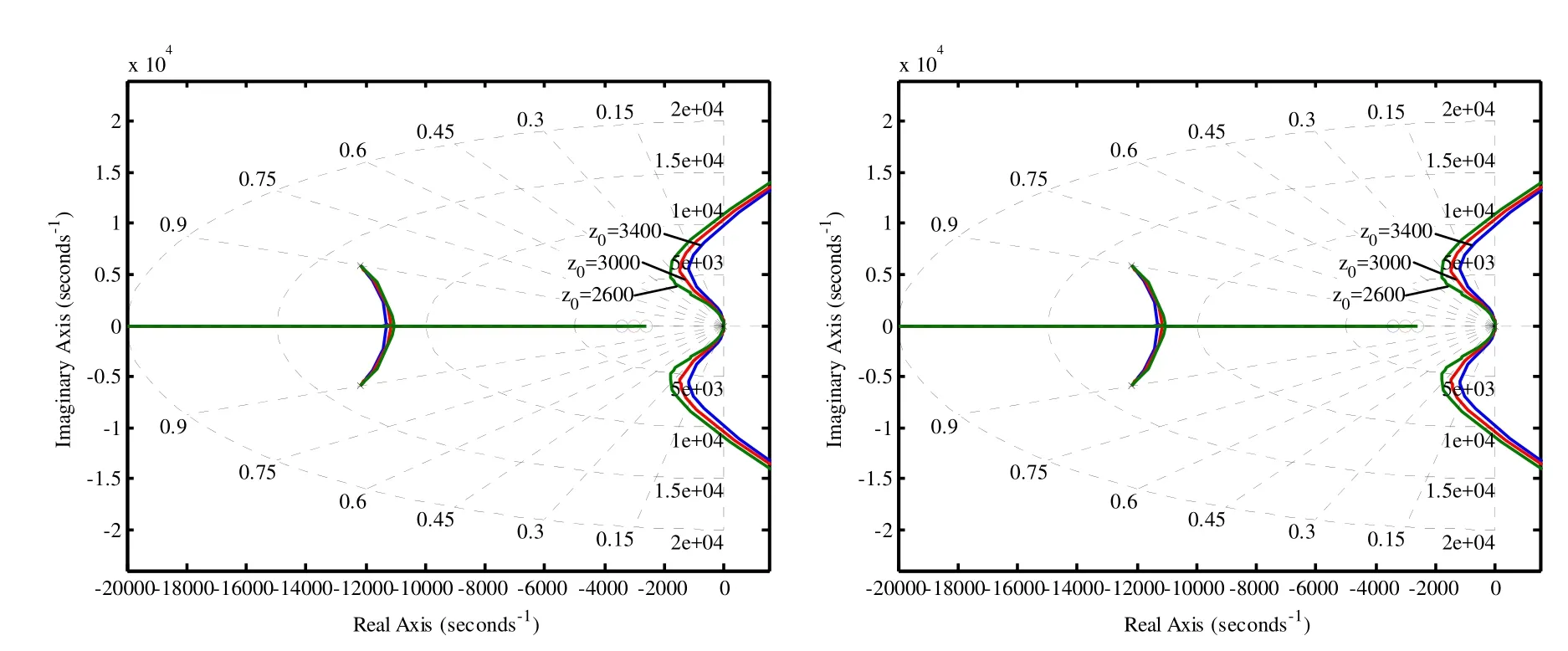
图7 不同开环零点z0下的根轨迹Fig.7 The system root locus with different parameters for z0
由图7可知,减少z0后,主导极点的根轨迹图明显趋向s域左半平面方向弯曲;由于z0距离开环非主导极点相对较远,难以对其根轨迹图有所影响,故非主导极点的根轨迹图没有太大的变化。由图7可知,随着z0的递减阻尼比ζ增大,系统稳定裕度提高。图10中闭环系统Bode图的相角裕度、幅值裕度可验证上文分析的正确性。
为优化1/T参数,选取图 7中ζ取得最大值时的z0,即当z0= 2 600时,分别取 1 /T= 0 .9ωr、0.84ωr、 0 .78ωr。得到如图8所示,闭环系统的根轨迹图。
由图8可知,正如式(7)、式(8)中的描述,随着1/T的递减,非主导极点的根轨迹图将快速地趋向虚轴方向;同时,主导极点的根轨迹图趋向 s域左半平面的零点方向;相对于前者,这种影响似乎过小,但对于提高系统的稳定裕度是不可或缺的,如图7所示,在优化参数z0时其值并没有大幅度改变,因为过度的减小z0虽可增强系统的阻尼效果,提高系统稳定裕度,但此时系统在基波频率处的相角会下降,导致并网电流的相位落后网侧电压。故在不违背配置原则(2)的思想下,可适宜减小1/T,加强非主导极点对系统的影响,或允许在一定的范围内非主导极点过分离点内进入实轴。
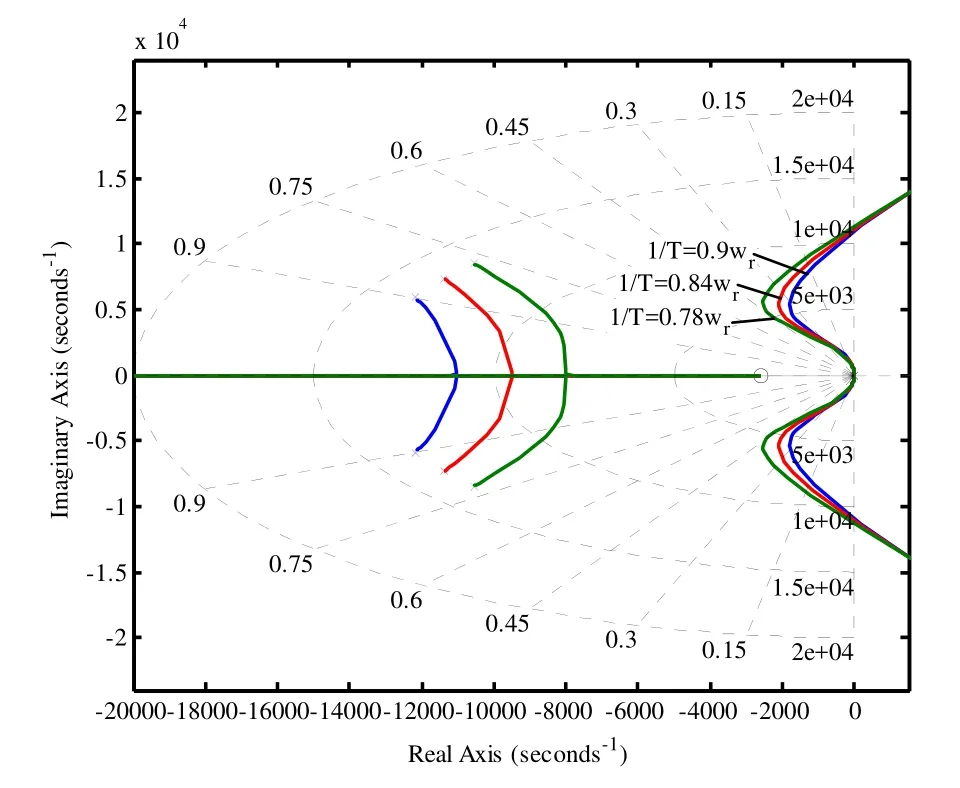
图8 1/T参数不同下的系统根轨迹Fig.8 The system root locus with different parameters for 8 1/T
由图 7、图 8及对系统频率特性曲线地分析可知:z0和1/T共同作用于系统的幅值裕度、相角裕度,影响系统的动态特性和稳定性。减小z0可加强附加零点的作用,即提高系统的稳态和动态特性,但会使并网电流在基波频率处的幅值增益和相角偏离1和0,无法与电网电压保持同相位;而z0取得过大,将减小系统的稳定裕度。为兼顾系统的稳态和动态特性,应合理地选择z0使系统获得良好的动态特性和一定的稳定性,同时减小1/T补偿系统的稳定裕度。
综合所述,按照上文提出的3条配置原则,结合根轨迹图即可整定和优化参数z0和1/T,在根轨迹图中选择K的值,再由公式(4)即可得到双闭环控制器参数。
由自控原理可知[28],二阶系统的相角裕度γ只与阻尼比ζ有关,且为ζ的增函数,通常要求相角裕度达到30°~60°,阻尼比ζ= 0 .4~0.8为宜。此时超调量适度,调节时间较短,相角裕度满足要求。按照以上步骤,要求系统的阻尼比ζ= 0 .51,选取最终优化参数:1/T= 0 .78wr,z0= 2 400。加入网侧电阻R1、R2后,最后得出参数优化后实际系统的根轨迹,如图9所示。
图 9中,在根轨迹与阻尼比ζ= 0 .51的交点处,根轨迹增益K= 8 .34× 1 011,此时,非主导极点虽越过分离点,但与主导极点复实部的比值分别为2.3和3.1;主导极点的根轨迹图趋向零点方向的变形程度增大,阻尼比ζ最大可取得0.55;综上所述,系统根轨迹图均满足上文提出3条配置原则。由公式(4)分别求得控制器内外环参数:KC= 2 5.347,KI= 9 47.62,KP= 0 .395;由此,画出优化后实际系统的Bode图,如图10所示。
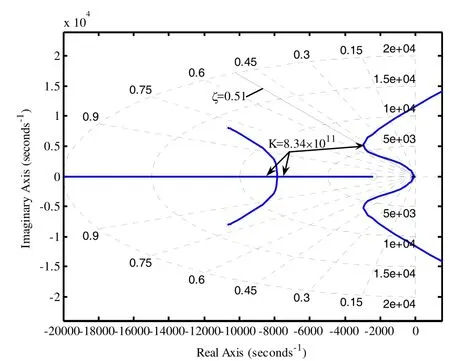
图9 参数优化后的实际系统根轨迹Fig.9 The actual system root locus after parameters optimization
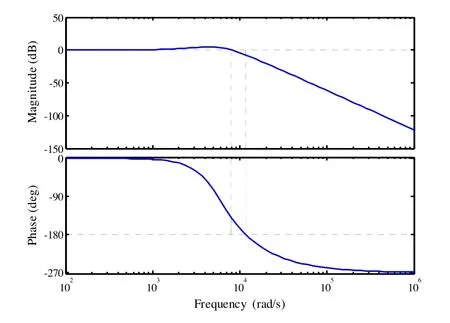
图10 优化后的系统Bode图Fig.10 Bode diagram of the system after optimization
由图10可知,系统在基波频率处的幅值和相角接近于1和0,并网电流具有较好的跟随性能,且系统的带宽较大;LCL滤波器谐振峰得到有效抑制;系统的相角裕度γ=39°,幅值裕度h=7.7dB,满足二阶系统稳定性要求;由此,验证了上文分析的正确性。
3 仿真实验
为验证本文控制器优化的参数是否合理,选取了一台实验样机,参数如表1所示,并对其进行仿真实验。
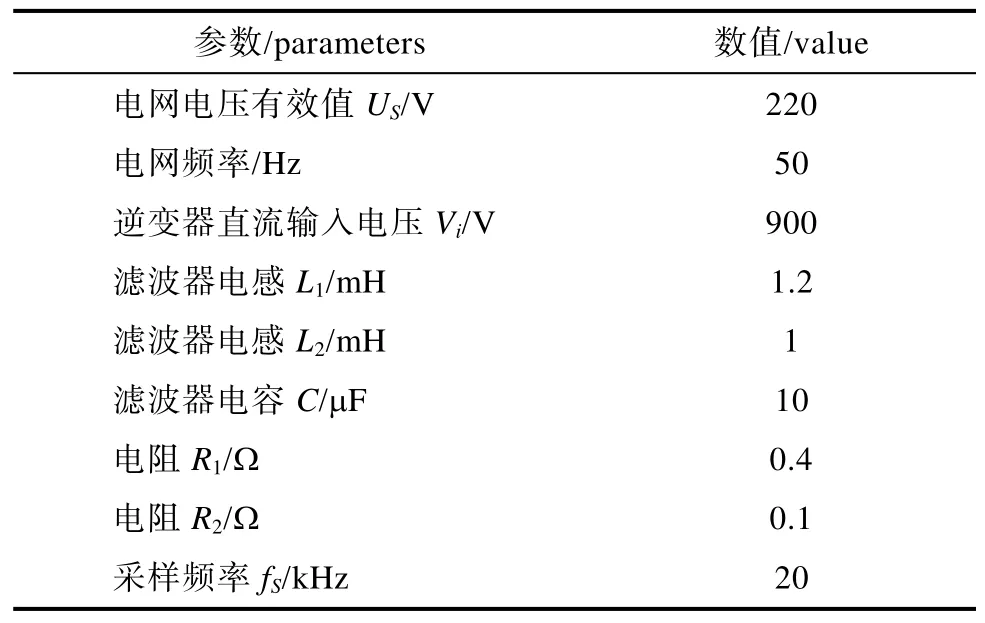
表1 并网逆变器实验样机参数Tab.1 The experimental prototype parameters of grid-connected inverter
在电网电压无有谐波的状态下,仿真实验表明,并网电流的THD不足2%。为验证控制器对谐波的抑制能力,参照文献[29],电网电压US共同注入 3、5、7、9、11、13、21、33、41次谐波,相对于基波幅值分别为10%、5%、3%、3%、2%、2%、1%、1%、0.25%,得到含有多次谐波、THD为 11.25%的网侧电压US;当指令电流有效值为25A时,得到并网电流i2的波形。如图11所示。
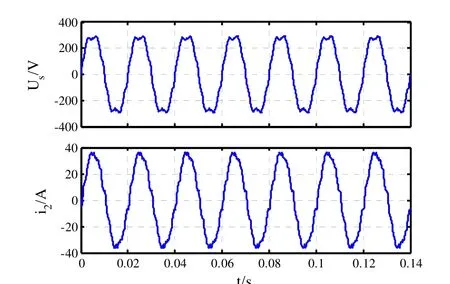
图11 含有多次谐波的电网电压US波形及并网输出电流i2波形Fig.11 voltage waveform of USwith multiple harmonics and waveform of grid-connected current i2
对并网输出电流i2进行快速傅里叶分析(FFT),得到各次谐波含量的百分比,如图12所示;其并网电流i2总谐波抑制比(THD)为7.26%。
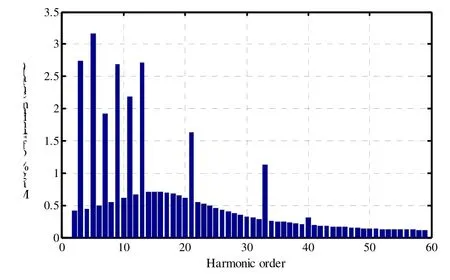
图12 并网电流i2谐波含量百分比Fig.12 Harmonic content percentage of grid-connected current i2
为验证并网电流突变时对网侧电压的敏感程度,在上述网侧谐波下,指令电流在峰值处由有效值20A突变到40A得到并网电流的动态响应波形,如图13所示。
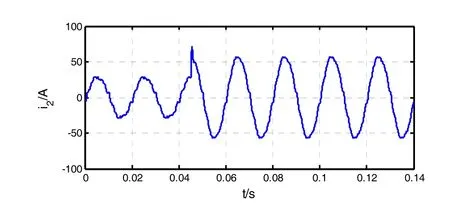
图13 并网电流的突变波形Fig.13 Mutation waveform of grid-connected current
由图13可知,并网电流突变过程的超调量仅为14%,动态调节时间小于2 ms,由此验证了并网电流的快速响应能力。对其进行其傅里叶分析,如图14所示,可得并网电流的THD仅为8.99%。
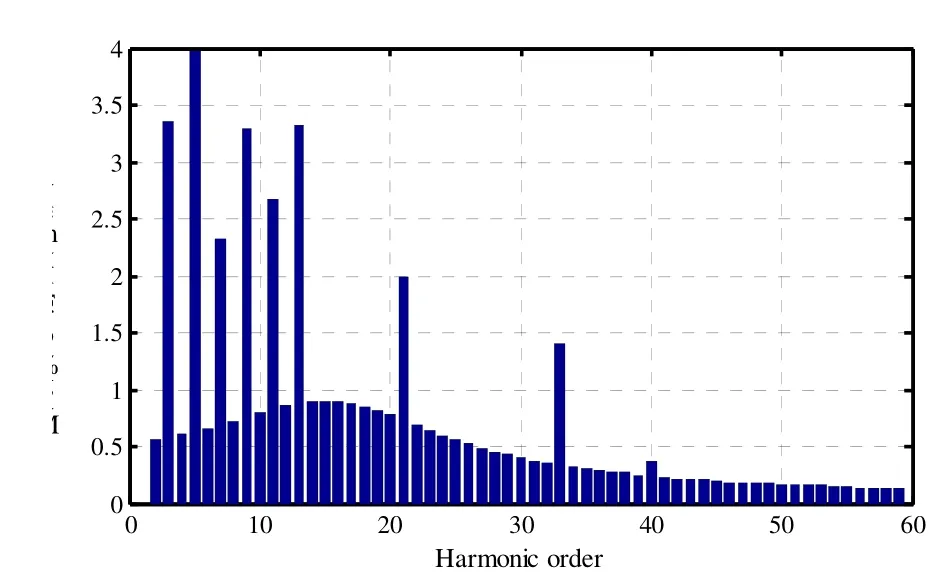
图14 并网电流i2突变时谐波含量百分比Fig.14 Harmonic content percentage for mutation waveform of grid-connected current i2
4 结论
本文通过分析系统根轨迹,应用频域法对逆变器双闭环控制的参数进行了设计和优化,得出以下结论:
(1)建立了逆变器控制系统模型。
(2)从工程实际出发,根据主导极点法提出3条闭环系统零极点配置原则,由此原则画出系统根轨迹图;通过根轨迹和频域分析法整定和优化控制器参数,分析了控制器参数对系统稳态和动态特性的影响。
(3)选择了一台样机进行仿真实验,仿真实验结果表明,本文所优化的控制器参数对于控制系统具有较好的鲁棒性、系统稳定性以及抑制谐波的能力。
