基于OFDM系统的Simulink仿真过程研究

季钰林，刘家威，傅俊杰

(成都信息工程大学，四川 成都 610103)

0 引言

随着人们对手机等其他无线终端网络设备要求的不断提高，通信质量和频谱利用率成为未来无线通信网络的主要目标和挑战。而正交频分复用系统（Orthogonal Frequency Division Multiplexing，OFDM）将多个信道分成若干正交子信道，提高信道利用率、对抗频率选择性衰落和噪声提高传输质量，因此他被认为是未来无线系统的最佳选择。为进一步提高信道利用率和传输速率，许多高性能的传输方案被引入到无线通信系统中，比如信道估计、MIMO技术等。

近些年来，国外很多公司企业都将OFDM技术应用于短波通信，并且开展了多载波传输技术，实验表明，短波通信中应用多载波传输技术可以极大提升通信质量。随着多载波技术的深入发展，国内很多企业也陆续研究基于OFDM技术的短波通信电台，以提高短波通信的抗截获性和传输可靠性[1]。本文通过仿真实验，主要探究了OFDM系统在不同条件下对系统性能的影响，通过对系统性能的分析，得出系统在什么条件下性能最好，对OFDM技术应用于短波通信具有积极作用。

1 OFDM系统的基本原理

OFDM（Orthogonal Frequency Division Multiplexing）即正交频分复用技术，实际上 OFDM是MCM（Multi Carrier Modulation）多载波调制的一种。其主要思想是：将信道分成若干正交子信道，将数据流分解成若干个独立的低速比特流，从频域上说就是分解成多个子载波，然后调制到每个子信道上进行并行传输。正交信道在接收端采用相关技术进行区分，可以减少子信道之间的相互干扰。每个子信道上的信号带宽小于信道的相干带宽，因此每个子信道可以看成平坦衰落，从而消除码间干扰[2]。而且由于每个子信道的带宽仅仅是原信道带宽的小部分，信道均衡变得相对容易。图1为OFDM（正交频分复用技术）系统的原理图。

图1 OFDM（正交频分复用技术）系统原理图Fig.1 OFDM (Orthogonal Frequency Division Multiplexing Technology) system schematic diagram

2 Simulink仿真过程

在仿真模型中首先随机产生整数序列，然后进行串并转换、进行QPSK调制、插入导频、进行IFFT运算、插入保护间隔，然后经过信道，移除保护间隔、进行FFT运算、加入信道估计、进行QPSK解调，在进行并串转换，最后进行判决输出[3]。

2.1 OFDM的循环保护间隔

OFDM的优势之一可以有效地对抗信号波形间的干扰，适用于多径环境和衰落信道中的高速数据传输。在OFDM系统中，为了最大限度的消除符号间干扰，在每个符号之间插入保护间隔（GI），如图2所示，将N-Ncp之后的数据复制到前端形成循环前缀，该循环前缀就是保护间隔，其长度一般要大于无线信道的最大时延拓展，这就使每一个符号的多径分量不会对下一符号造成干扰。

图2 循环前缀原理图Fig.2 Schematic diagram of cyclic prefix

在实际应用中，首先要加入循环前缀形成保护间隔再送入信道中进行传输，这可以有效的对抗码间串扰[4]，即在OFDM符号开始部分插入其后部分，形成循环前缀。在接收端，首先将接收到信号的前缀丢弃，然后对剩余的部分进行傅里叶变换。

2.2 信道估计

在 OFDM 系统的相干检测中需要对信道进行估计，信道估计的进度将直接影响整个系统的性能。信道预测方法可分为线性预测和非线性预测[5]。非线性预测算法是将样值序列分解为信号子空间和噪声子空间，对信道系数进行预测，此类算法复杂度高、计算量大且不易实现；线性预测算法抽样速率低，预测距离较长，但要求信道的统计特性已知[6]。如图 3所示的信道估计仿真图所示，本次研究以 LS信道估计方法对未来时刻进行预测。

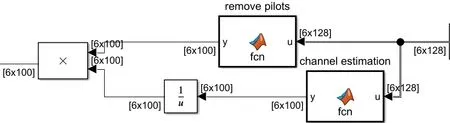
图3 信道估计仿真图Fig.3 Channel estimation simulation diagram

2.3 信道

在通信理论中，常用的仿真信道模型为AWGN和RAYLEIGH。AWGN即为仅含高斯白噪声的信道，这是在通信理论中无法避免的噪声，其功率谱密度为均匀函数，概率密度函数呈正态分布[7]。RAYLEIGH信道是一种无线电信号传播环境的统计模型。从基站发出的信号经过反射、折射、散射等多条路径传播到达接收机后，总信号的强度服从瑞利分布。同时由于接收机的移动及其他原因，信号强度和相位等特性又在起伏变化，故称为瑞利衰落，这就使得接收信号的误码率大大增加。

3 仿真结果与分析

本次实验基于Simulink仿真，得到不同参数下的仿真数据（如下系统参数值和仿真数据）。其中参数选择有子载波数、循环前缀长度、导频长度、信道，本次实验的目的就是对比在不同循环前缀长度、不同导频长度、不同信道下对误码率的影响[8]。（snr表示信噪比；err表示误码率）。

表1和表2表示在高斯信道下循环前缀长度为8，导频长度为16下的实验数据，信噪比取0到15，共16组数据。

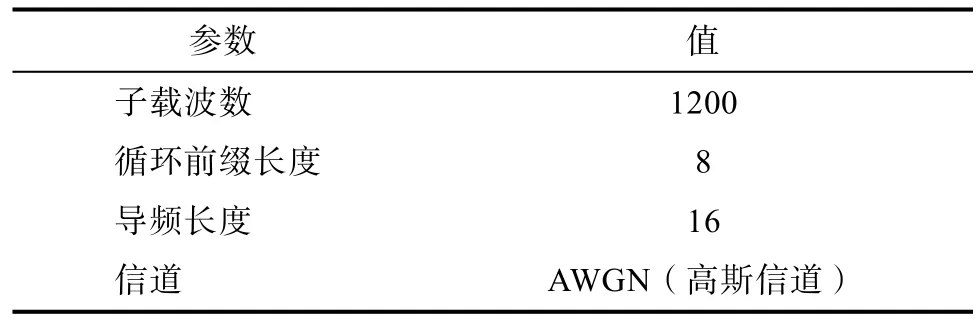
表1 高斯信道系统参数值Tab.1 Gaussian channel system parameter values

表2 高斯信道系统仿真数据Tab.2 Gaussian channel system simulation data

表3和表4表示在瑞利信道下循环前缀长度为8，导频长度为16下的实验数据，信噪比取0到15，共16组数据。

表3 瑞利信道系统参数值Tab.3 Rayleigh channel system parameter values

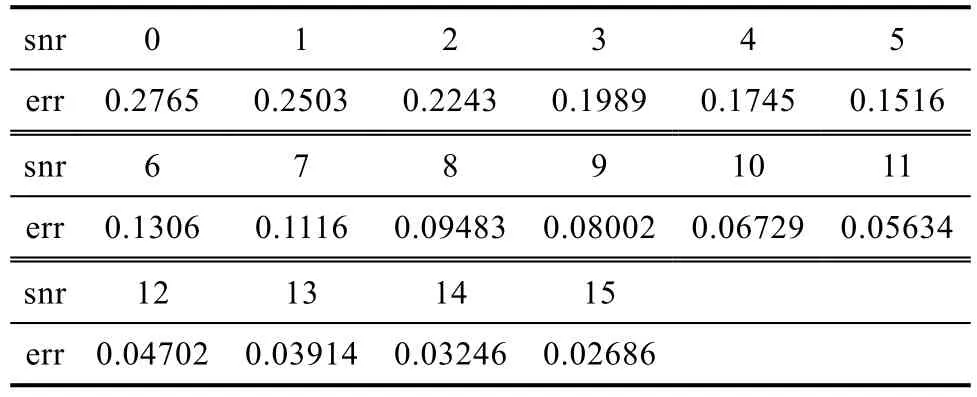
表4 瑞利信道系统仿真数据Tab.4 Rayleigh channel system simulation data

表5和表6表示在瑞利信道下不添加循环前缀，导频长度为16下的实验数据，信噪比取0到15，共16组数据。

表5 不加循环前缀瑞利信道系统参数值Tab.5 Rayleigh channel system parameter values without cyclic prefix

表6 不加循环前缀瑞利信道系统仿真数据Tab.6 Simulation data of Ruili channel system without cyclic prefix

表7和表8表示在高斯信道下循环前缀长度为 8，不添加导频长度、不采用信道估计下的实验数据，信噪比取0到15，共16组数据。

表7 循环前缀为8时瑞利信道系统参数值Tab.7 Rayleigh channel system parameter values when the cyclic prefix is 8

表8 循环前缀为8时瑞利信道系统仿真数据Tab.8 Rayleigh channel system simulation data when the cyclic prefix is 8

由上实验数据在MATLAB中得到如图4的性能图，横坐标信噪比（SNR）和纵坐标误码率（BER），其中黑色线表示在不采用信道估计时瑞利信道的实验数据；绿色线表示在不采用循环前缀时瑞利信道的实验数据；蓝色线表示既采用信道估计也采用循环前缀下的瑞利信道的实验数据；红色线表示仅在高斯信道下的实验数据。

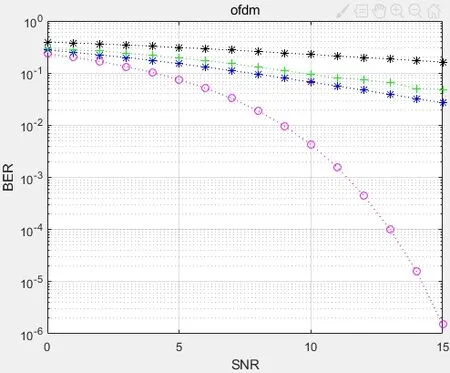
图4 仿真结果Fig.4 Simulation results

4 结论

通过本次对OFDM系统进行Simulink仿真研究，对OFDM系统中信号的产生、调制和解调模块，在高斯和瑞利信道下进行仿真，得到相应的数据，并针对得到的数据仔细研究了误码率。通过一系列仿真和分析证实了：（1）对高速数据流进行串并转换，增加数据符号的比特信噪比，提高对抗多径时延能力，降低信号在传输过程中的误码率；（2）采用循环前缀来填充保护间隔，可以提高对抗多径传播带来的影响，降低信号在传输过程中的误码率；（3）利用 LS算法对信道进行估计，可以降低信号在传输过程中的误码率；（4）信号只在高斯信道下传输性能是最优的。当然OFDM系统也存在一定的缺陷，对相位噪声和载波频偏非常敏感和存在均峰值过大。这对于我们以后的研究指明了方向。