基于联合子空间对齐与极限学习机的无监督领域自适应平台研究

陶 洋，胡 昊，鲍灵浪

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引言

传统分类方法一般是从训练样本中学习分类模型，然后直接将其应用于测试样本分类。当训练样本和测试样本满足独立同分布基本假设时，分类模型可以获得很好的分类效果[1]。但是，在实际应用中，由于各种因素（例如不同的视觉分辨率和照度）不可能保证训练样本始终与测试样本具有相同的分布。当它们具有不同的分布时，获得的模型通常会失效[2]。如图 2显示了不同领域下图像之间的差异。

本文重点研究无监督领域自适应学习，更符合现实场景应用。在解决源数据与目标数据分布不均的问题方面，具体分为更改数据表示形式和修改训练分类器方式。这两类方式的迁移学习单独执行的效果并不是非常理想，这是因为数据分布不同而导致的。同时在现实应用过程中的噪声会影响分类器和迁移学习算法的稳定性，导致分类器鲁棒性不佳。而且传统的迁移学习算法仅仅是从单纯的改变数据表示进行迁移进行的，而忽略了结合分类器设计，不能使得分类器参数适合领域自适应，提升迁移学习的效果。

为了克服传统领域自适应方法的弊端，提出了一种分类器联合子空间学习方法，该方法将数据表示迁移方法和分类器设计相结合。具体来说，首先分解极限学习机分类器输出层权重，设计一个灵活的极限学习机分类器。然后使得输入层具备提取共有特征的能力，在分类器的隐含层中利用子空间对齐方法将源数据和目标数据被转换为一个公共子空间，其中每个目标数据都可以通过源域中的数据线性地重构。本文在重建矩阵上施加低秩约束，以便可以保留数据的全局结构。低秩约束的设计还确保了来自不同域的数据可以很好地交织，这有助于显着减小域分布的差异[3]。本文同时对噪声进行建模，用来消除噪声对模型产生的负面影响，过滤噪声信息[4]。所提出的方法如图1所示。该方法称为联合子空间对齐与极限学习机无监督领域自适应（Joint Suspace Alignment and Extreme Learning Machine，JSAELM）。

1 极限学习机

式（1）中H∈R，g(·)为激活函数。根据最小二乘法求解极限学习机输出层权重β的目标函数为：

式（2）中C为预测误差项的惩罚系数，同时为避免参数过拟合对参数β施加正则项，式（3）是经典的岭回归正则化最小二乘优化问题，令目标函数对β的梯度为0，可得：

式（4）中的β可以根据Moore-Penrose广义逆矩阵的方法得到最优解。当训练样本数n与隐含层神经元个数L大小不同时，求解β存在两种情况：

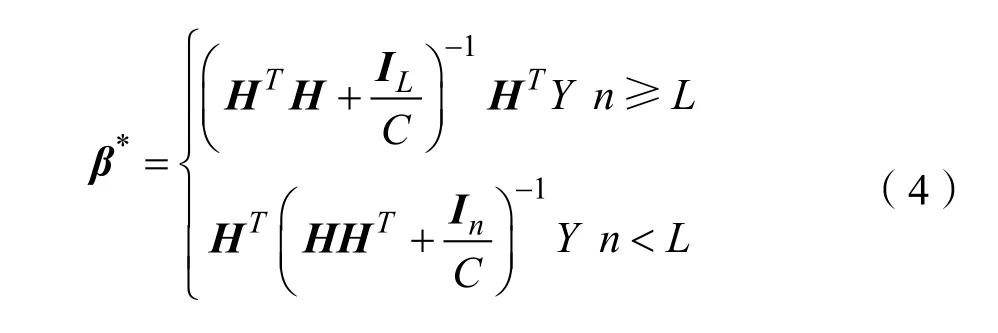
2 联合子空间对齐与极限学习机无监督领域自适应

2.1 模型结构

图1 JSA-ELM模型结构图Fig.1 Structure of JSA-ELM mode

2.2 ELM的领域不变隐含层权重学习

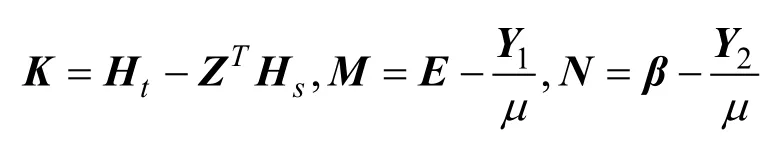
2.3 具有迁移能力的 ELM 输出层权重学习

根据第2.2节求得的ELM的领域不变隐含层权重W可计算出源域和目标域相应的隐含层特征：

其中，g(·)表示隐含层激活函数。为进一步提升 ELM 分类器的跨领域知识迁移能力，JSA-ELM 将输出层权重的学习过程中联合子空间对齐方法，使得输出层权重具有较好的迁移能力。

2.3.1 极限学习机源域分类损失

在极限学习机源域分类器学习过程中，仅有源域样本包含标签信息。因此，跨领域分类器参数通过带标签的源域样本进行训练。定义源域样本数据与数据标签为{xs, ys} ，根据第1节中的极限学习机算法，分类器输出层权重的损失函数可表示为：

其中，Hs为源域的隐含层特征表达。为了有效的联合子空间学习，本文采用一种更灵活方法，将输出权重矩阵β分解为两个矩阵β和R。因此，将式（7）转换得到优化模型：

2.3.2 子空间领域对齐

本文使用低秩约束来强制 Z具有这样的结构。因此本文可以得到：

式（9）有利于获得xs和xt的一致表示，以便源数据和目标数据很好地对齐。由于秩最小化问题是非凸问题，因此式（9）中的问题是 NP-难问题。如果Z的秩不太大，则式（9）等效于：

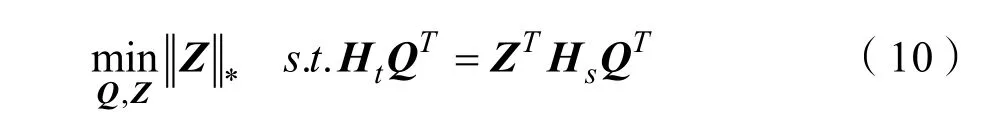
其中Z*是矩阵的核范数。为了减轻噪声的影响，本文引入矩阵E对噪声进行建模，并对E施加稀疏约束，然后将式（10）更改为：

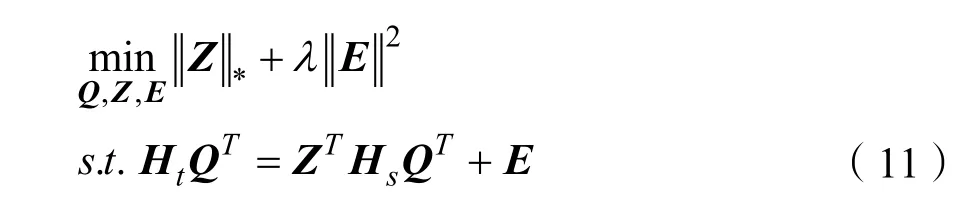
2.3.3 目标函数求解优化

联合分类器式（8）和子空间对齐式（11），得到求解跨领域分类器输出层权重的目标函数：

其中α,C,λ为惩罚系数。解决式（12）需要通过固定其他变量来迭代更新每个变量。对目标函数式（12）加入辅助变量Z1转换为：

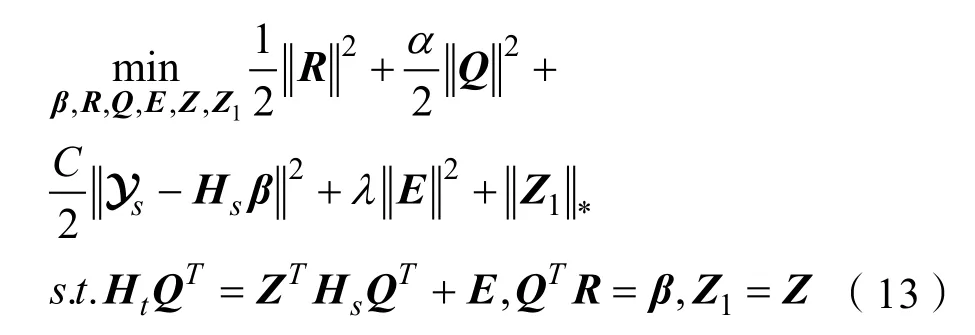
式（13）的增广拉格朗日函数L为：

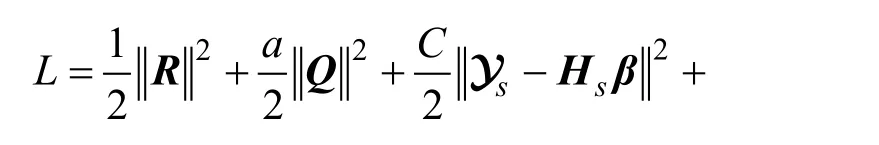
其中Y1，Y2和Y3是拉格朗日乘数，而μ＞0是惩罚参数。通过交替更新变量，并固定其他变量来最小化拉格朗日函数L。满足收敛条件后，迭代将停止。解决式（14）的主要步骤如下：

Step.1更新Q，解决式（15）更新参数Q：

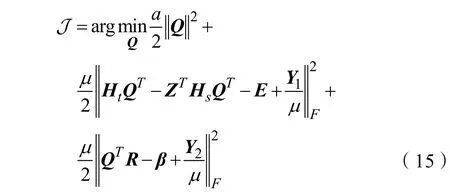
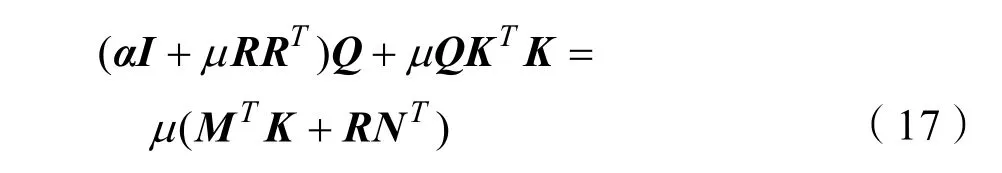
式（17）为西尔维斯特方程（Sylvester Equation），可以采用文献[7]中的求解方式对式（17）进行求解获得Q。

Step.2更新Z，解决式（18）更新参数Z

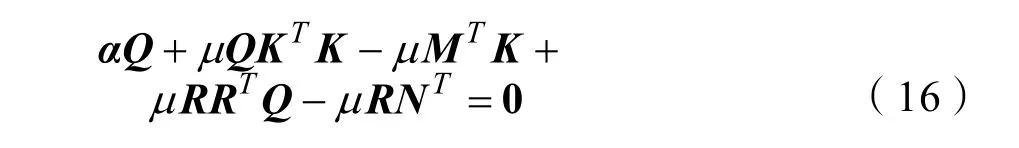
式（16）可进一步转化为：

则：

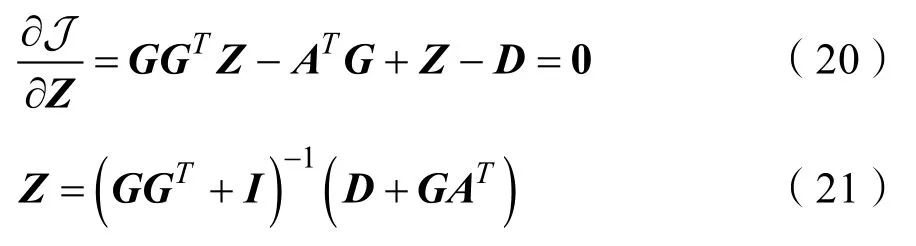
Step.3更新Z1，解决式（22）更新参数Z1：

式（22）的闭式解为：

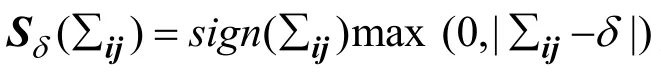
Step.4更新E，解决式（24）更新参数E：

Step.5更新R，解决式（27）更新参数R：

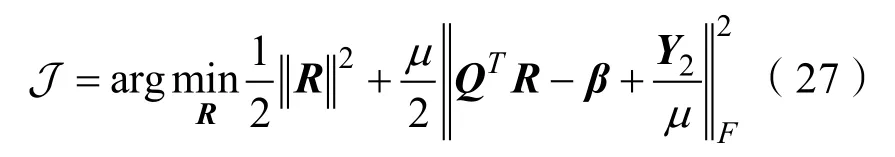
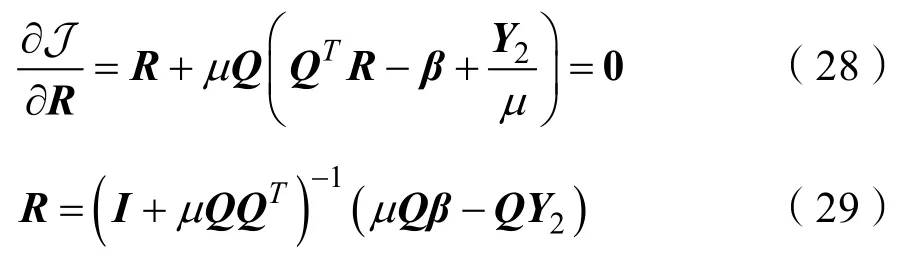
Step.6更新β，解决式（30）更新参数β：

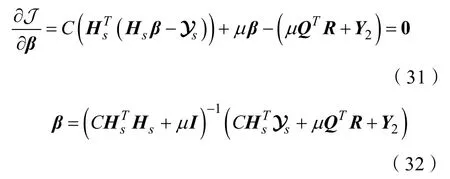
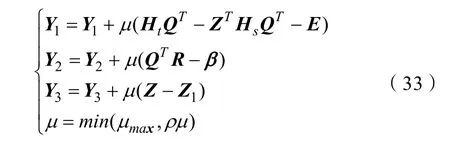
联合子空间对齐与极限学习机无监督领域自适应算法如算法1所示。

算法1 JSA-ELM执行流程

输入：

隐藏层输出矩阵Hs,Ht；标签矩阵 ys；

平衡参数α,λ,C,； 隐藏子空间푑 的尺寸。

初始化：

循环执行：

更新参数Q，根据式（17）

更新参数Z，根据式（21）

更新参数Z1，根据式（23）

更新参数E，根据式（26）

更新参数R，根据式（29）

更新参数β，根据式（32）

收敛则停止

输出：

输出具有迁移能力的权重矩阵β

3 实验结果与分析

3.1 实验数据集及设置

为了验证 JSA-ELM 方法的性能及其泛化能力，在4个公开数据集上对JSA-ELM进行验证。这些数据集已被大多数领域自适应研究学者广泛采用。表1列出了各个基准数据集的统计数据。

表1 JSA-ELM实验数据集Tab.1 Experimental dataset

Office数据集是视觉自适应领域中通用的基准数据集，由三个不同对象域组成：Amazon在线商家下载的图像，Webcam网络摄像头拍摄的低分辨率图像和DSLR高分辨率图像，共包含31个类，4,652张图像[8]。

Caltech-256是用于对象识别的标准数据集，包含256个类别的30,607张图像[9]。在实验中，本章使用了Gong等人提供的Office和Caltech数据集，该数据集是由三个 Office数据集和一个Caltech数据集中相同的十个对象类别组成的[8]。将四个不同的域命名为 C(Caltech-256)，A(Amazon)，W(Webcam)和 D(DSLR)。通过源域和目标域的组合，构造了4×3=12个跨域对象数据集C→A，C→W，C→D，A→C，……，D→W。

USPS数据集包含7,291个训练样本和2,007个测试样本，大小为16×16像素。MNIST数据集由 60,000个训练样本和 10,000个测试样本组成，大小为28×28像素[10]。从图3可以看出USPS和MNIST数据集中样本之间的分布不同，它们共享10种类型的数字样本。按照文献[11]的实验设置，我们通过随机选择 1,800个样本作为 USPS中的源数据并随机选择2,000个样本作为MNIST中的目标数据来构建 USPS(U)→MNIST(M)数据集。并通过切换源/目标对获得另一个数据集MNIST(M)→USPS(U)。为了在源数据和目标数据之间共享相同的特征空间，我们将 USPS和MNIST数据集的所有图像缩放为16×16大小，并且每个图像都由一个256维特征向量表示，该向量对灰度像素值进行编码。数据集的示例样本如图3所示。

图2 数据集示例图Fig.2 Example samples of datasets

3.2 实验结果分析

3.2.1 物体目标识别

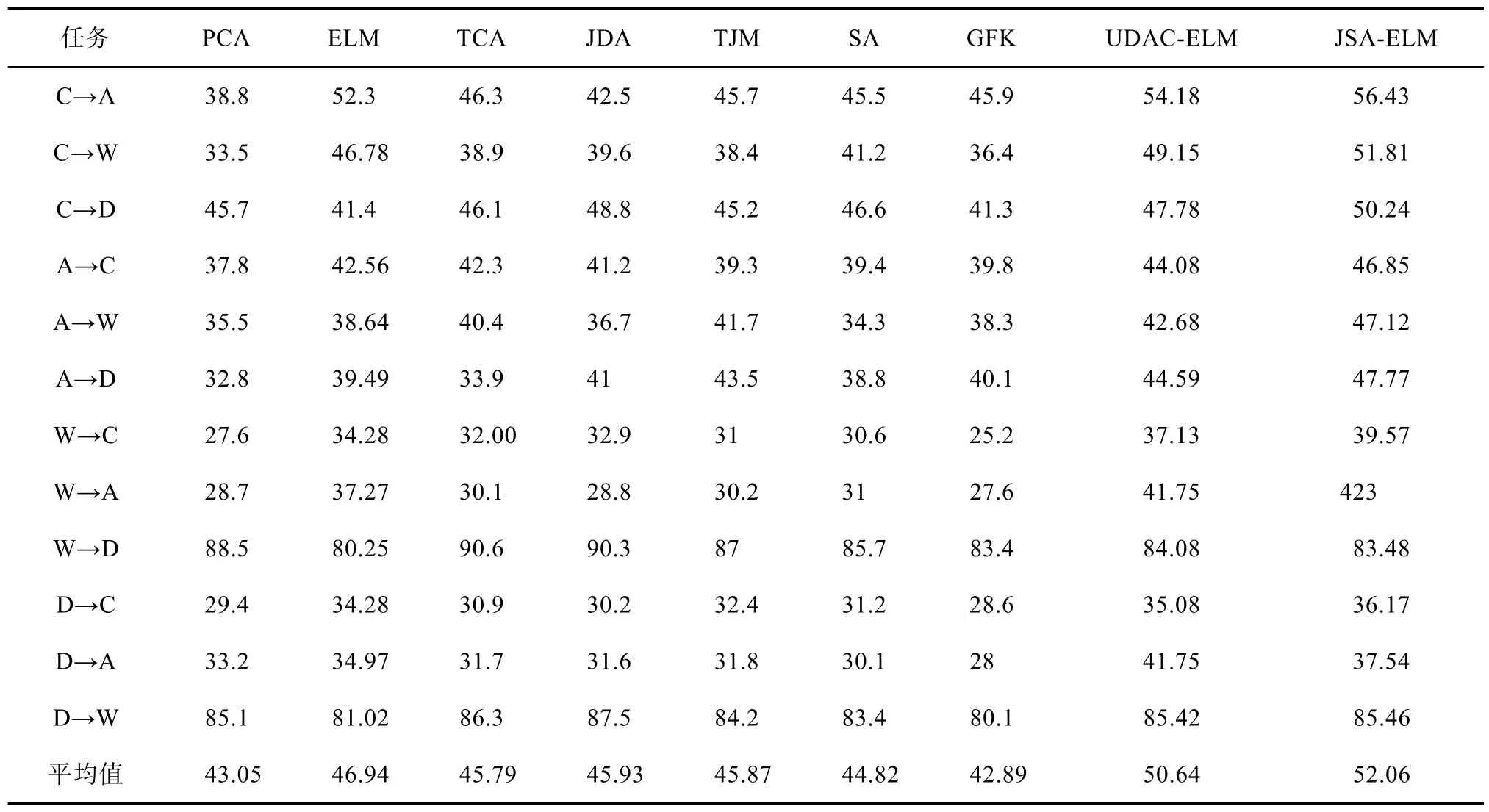
表2 Offce+Caltech10数据集的分类准确率（%）Tab.2 Classification accuracy of Offce+Caltech10 datasets

图3 JSA-ELM参数敏感度分析Fig.3 Parameter sensitivity analysis of JSA-ELM

为了验证本章提出方法的有效性，本文在物体图像数据集上做了9个自适应分类实验。包括经典的主成分分析算法（PCA）；迁移成分分析算法（TCA）和联合分布适配法（JDA）的概率分布适配法；迁移联合匹配算法（TJM）为代表的特征选择的方法；子空间学习法则选择子空间对齐法（SA）和测地线流式核算法（GFK）算法进行实验；同时还对比了基础的极限学习机（ELM）和最新的极限学习机领域自适应模型（UDACELM）[12]。

实验中所有比较方法的最佳参数都是根据其原始论文来设置。对于本章提出的方法，本文设置了隐含层维度为 256，C为 0.1，μ为 0.1。选择全部源域作为训练数据，在训练前做相应归一化处理。选择所有目标域样本作为测试数据，重复进行10次实验并取平均值，实验结果如表3所示。

从表3可以看出，本章提出的联合子空间对齐与极限学习机方法（JSA-ELM）平均分类准确率优于其他对比方法。JSA-ELM 的平均分类准确率为52.06%，与其基本的ELM和SA相比平均精度提高了5.12%和7.24%。单纯的ELM分类器算法、分布对齐方法（TCA、JDA和TJM）和子空间学习方法（SA和GFK）的性能普遍比JSA-ELM差。这表明参与对比的传统分类器和领域自适应方法都有一定的局限性，导致领域偏差对分类器影响较大。UDAC-ELM在流形学习之后，仍然存在较大的域偏移。在不同图像数据集上进行验证表明 JSA-ELM 能够显着减少领域自适应问题中的分布差异。

3.2.2 手写数字识别

在手写体数字识别实验中，本文选择极限学习机（ELM）、迁移成分分析算法（TCA）、联合匹配算法（TJM）、子空间对齐法（SA）、测地线流式核算法（GFK）和无监督域自适应极限学习机（UDAC-ELM）作为对比方法。所有对比算法都是根据其原始论文来设置的最佳参数。对于本章提出的方法，设置隐含层维度为32，C为0.1，μ为0.1，选择全部源域图像作为训练数据，并做相应归一化处理。选择所有目标域样本作为测试数据，重复进行10次实验并取平均值，实验结果如表3所示。

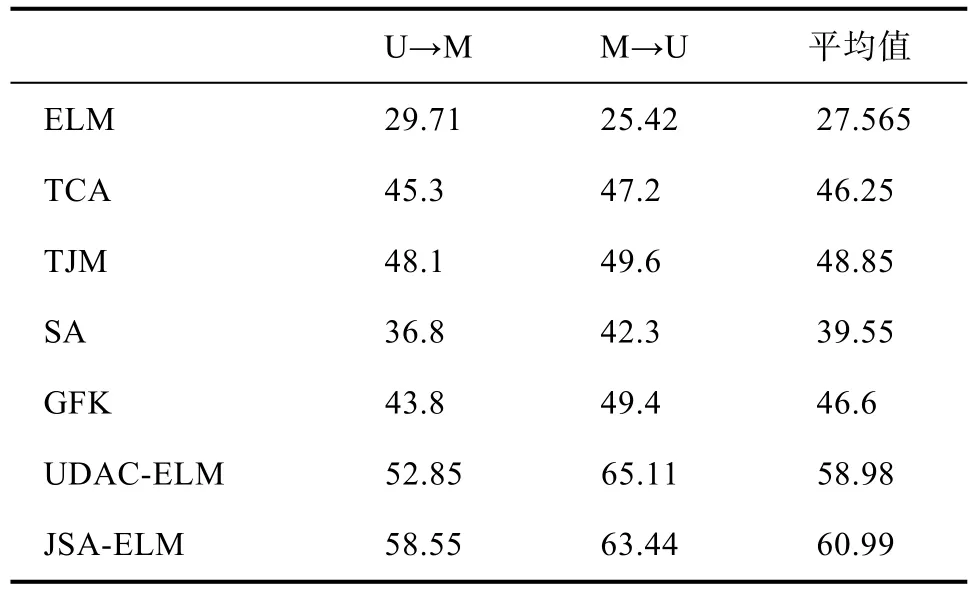
表3 USPS和MNIST数据集的分类准确率（%）Tab.3 Classification accuracy of digital datasets

从表 2中可以看出，本章提出联合极限学习机和子空间对齐（JSA-ELM）在平均分类准确率上优于其他对比方法。JSA-ELM在分类性能上远远高于SA和ELM算法，比最新的UDAC-ELM提高了2.01%。这表明SA-ELM能充分利用子空间对齐方法提升分类器对领域偏差的鲁棒性，有效地减小领域间的分布差异，提高算法的分类性能。

3.3 参数分析

本节分析 JSA-ELM 在不同类型数据集上的参数敏感性。在不同类型的数据集上的结果已证实，固定的C=0.1和μ=0.1并将所有学习率设置为0.001，对于所有任务都是足够的。因此，我们仅评估其他三个参数α，λ和隐藏层数。我们在USPS→MNIST和 A→D数据集上进行实验，如图3所示。实线是使用不同参数在JSA-ELM上的准确度，虚线表示在每个数据集上通过最佳基线方法获得的结果。在其他数据集上也观察到类似趋势。从图 3（a）和（b）可以看出，与最佳基准方法相比，可以选择大范围的α和λ获得更好的结果。图 3（c）显示出了隐藏层参数h与精度之间的关系，可以看出本模型仅需较少的隐藏层数就可以达到较好的效果，表示只需较少的计算资源消耗。

4 总结

本文主要针对领域自适应问题进行了深入研究，并结合子空间学习、极限学习机提出了联合极限学习机和子空间对齐的无监督领域自适应方法。该方法将更改数据表示方法和分类器设计相结合。针对 ELM 的输出层参数进行了自适应学习，进一步增强其迁移能力。首先通过利用ELM-AE获取用于提取域不变性特征权重替代ELM初始化随机权重；然后拆分ELM输出层权重使其更加的灵活；联合极限学习机分类器拆分后的输出层中利用子空间对齐方法将源数据和目标数据转换为一个公共子空间，其中每个目标数据都可以通过源域中的数据线性地重构。在重建矩阵上施加低秩约束，以便可以保留数据的全局结构，同时低秩约束的设计还确保了来自不同域的数据可以很好相互表示，这有助于显着减小域分布的差异。并且在公开数据集上的实验验证了该算法的可行性。