东北亚五国货币汇率联动的实证研究——基于VAR-GARCH-BEKK方法的分析

陈天宇 杨懿靖 王雅杰

（1.南京大学，江苏 南京 210093；2.哈尔滨工业大学，黑龙江 哈尔滨 150001）

一、引言

在当前经济全球化不可逆转的国际环境下，中国与世界各国的经贸往来日趋紧密，在整个世界经济中的作用愈发凸显。2013 年，中国提出“一带一路”倡议，既利于促进相关国家贸易一体化，同时也对与中国相关的区域经济一体化和以地缘为基础的区域经济合作提出更高的要求。东北亚区域是共建“一带一路”倡议中的重要一环，其经济往来和贸易合作倍受重视。2018 年，习近平总书记发出构建东北亚经济圈的倡议，2019 年又强调加快形成以国内大循环为主体、国内国际双循环相互促进的新发展格局。在此背景下，中国积极参与东北亚各国经贸合作，与东北亚各国的贸易呈现快速发展的势头。2019 年，中国与东北亚经济体之间的进出口贸易总额达7219.86亿美元，占我国出口贸易总额的15.81%，而中国与东北亚各国的投资总量和数目也在稳步增长中。随着东北亚国家间的经济与贸易联系日趋紧密，各国货币汇率的波动及其之间的相关性也会越来越显著，非常具有研究价值。事实上，随着“一带一路”建设的不断深化，人民币的国际化进程也不断推进，有关人民币与其他国家货币汇率之间关系的研究正在日益得到关注。已有研究大多关注人民币与欧元、日元等发达市场货币的联动关系（郭珺和滕柏华，2011），人民币与周边国家和地区（韩国、东盟、两岸四地）的汇率波动关系（王中昭和杨文，2014），人民币与俄罗斯、中亚地区货币传导溢出效应（张钰和张栋，2020），人民币与RCEP 主要成员国货币汇率动态联动性研究（万正晓和倪阳，2020），那么，东北亚区域国家货币汇率是否具有联动性？本文首次构建五元VAR-MGARCHBEKK模型，研究中国、日本、俄罗斯、韩国、蒙古等东北亚五国之间的汇率联动机制，考察东北亚五国货币汇率是否存在均值溢出和波动溢出，分析研究成果并提出相应的政策建议。

二、文献综述

有关汇率波动联动性的研究方法经历了一个发展阶段。Granger（1986）提出协整分析方法，Engle（1982）提出自回归条件异方差模型（ARCH），Engle& Granger（1987）建立向量误差修正模型。此后，学者大多在此基础上进行汇率波动研究。Baillie &Bollerslev（1989）首次将协整理论应用于对汇率的研究，证明七种汇率存在长期的协整关系。对于汇率的波动效应，Harvey et al.（1994）首先提出随机波动模型（SV）并用于分析美元、英镑、法郎、马克的波动溢出效应。国内学者丁建平和杨飞（2007）也在GARCH模型的基础上利用随机波动模型总结出主要货币的汇率波动特征和人民币与主要货币联动的权重变化。此后，有关学者利用向量自回归（VAR）模型中的方差分解（VDC）和脉冲响应函数揭示不同货币汇率之间的波动传递（Hurley & Santos，2001；Nikkinen et al.，2006），并在此基础上构造溢出指数衡量汇率的波动溢出效应（McMillan & Speight，2010；尹力博和李勍，2017）。近几年国内外学者大多采用改进的多元GARCH模型对不同时间序列的汇率动态联系进行分析，如VC-MVgarch 模型（Kitamura，2010）、多变量非对称DCC-GARCH 模型（Tamakoshi & Hamori，2014）、Copula-GARCH 模型（Sehgal et al.，2017）、VAR-DCC-MVGARCH 模型（叶芳童和童星宇，2020）等，也有学者采用DCC-BEKK 模型和MVGARCHBEKK 的方法进行分析（Alvarez-Diez et al.，2019；裴斌等，2021）；也有学者利用马尔可夫转换模型进行汇率联动研究（Keddad，2019）；还有学者基于构造汇率动态网络结构的思想，利用最小生成树（Mizuno et al，2006）和基于多元互相关方法的汇率联动网络模型（麦勇和陈欢，2016），总结全球汇率波动的特点并发现货币联动的地理邻近属性和溢出效应。

国外学者对汇率联动的研究对象主要是欧美货币，比如美元、欧元、英镑、法郎、马克、瑞士法郎等，也有涉及南亚和东南亚国家货币汇率之间的联动关系研究，但对人民币与其他货币联动性的研究较少。国内学者在该方面已进行丰富的探索，有探究人民币与美元等发达市场货币、周边国家货币（韩国、东盟、两岸四地）的联动关系，也有研究人民币在岸、离岸市场内部及其与其他货币的溢出效应（周先平和李标，2013；阙澄宁和马斌，2015）。现有文献中缺乏对东北亚各国货币汇率联动的研究，而东北亚地区是世界重要的经贸区，经济贸易往来日趋紧密，各国货币汇率的波动及相关性日趋显著，具有很大的研究价值。

三、东北亚五国货币汇率联动的经济基础

（一）经济总量增长态势趋同是汇率联动的环境基础

就经济总量来看，近年来，东北亚五国经济体总量不容小觑，在世界经济格局中占有重要地位。东北亚经济总量格局呈现两强引领下的“2+3”模式，即两个经济强国：中国和日本，三指韩国、蒙古和俄罗斯。同时，东北亚经济体总量保持中高速增长，仅有少量年份呈现负增长。

如图1所示，中国自2010年超过日本成为东北亚经济总量最大的国家后，一直遥遥领先，且保持中高速增长；日本则在2010年后稳定在第二位，总量呈略微下降趋势。俄罗斯与韩国经济总量位于第二梯队，俄罗斯2015年总量衰退被韩国赶超，随着经济复苏，2019 年超越韩国，两者总量相差不大。第三梯队为蒙古国。蒙古国在2011～2013 年经历一轮超过10%的经济增长，2015开始回降至5%以下。东北亚各国经济在总体上受到2008 年全球金融危机的影响，于2009 年跌到谷底，此后几年逐渐回升，并保持稳定。近五年来，从人均GDP 上看，东北亚各国排名变化不大，经济总量稳步增长，给各国经济进一步合作创造很好的外部条件，也为货币汇率的联动提供可能。

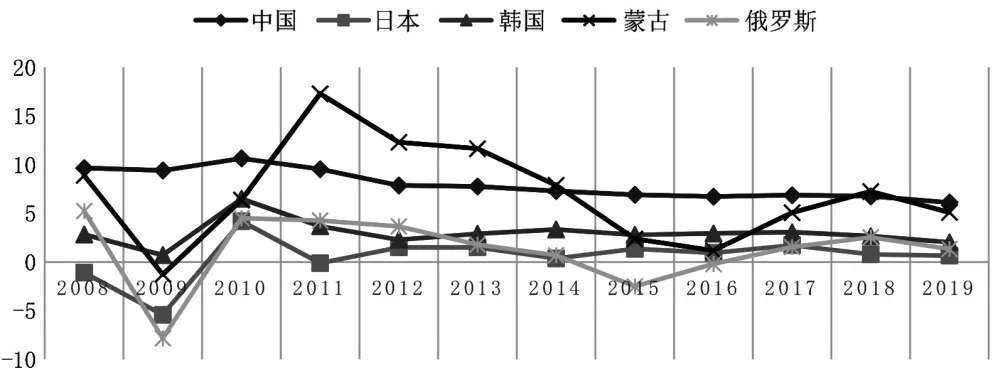
图1 2008～2019年东北亚五国GDP增长走势

（二）东北亚五国之间的贸易投资联系增强是汇率联动的现实条件

1.东北亚五国的贸易往来日益密切。2013年“一带一路”倡议提出以来，中国与东北亚的贸易合作发展速度加快。一方面，2014～2019 年间，中国成为东北亚其他四国的第一大贸易伙伴国。其中，占日本进出口总额维持在20%左右，占韩国进出口总额的23%左右，占俄罗斯进出口总额的20%左右，占蒙古进出口总额达65%。另一方面，东北亚其他四国在中国的贸易地位也不断攀升。日本作为中国的重要贸易伙伴国，地位从2014 年的第5 位升至2019 年的第4 位，占中国进出口总量比例维持在7%左右；而韩国则成为中国的第6大贸易伙伴，占中国进出口总量约6%；俄罗斯也进入中国前十位贸易伙伴，占中国进出口总量的2.42%；蒙古国在中国的贸易总量也稳步提升。

2014～2019 年间，东北亚其他四国的贸易合作也不断加强。韩国是日本的第三大贸易伙伴，日本是韩国进口排名前三位的国家；日本、韩国成为俄罗斯第七、八大贸易伙伴，占俄罗斯进出口总量分别是3.7%和2.9%左右；俄罗斯仅次于中国成为蒙古的第二大贸易伙伴，占蒙古进出口总量约13.15%，日本则成为蒙古第三大贸易伙伴，占蒙古进出口总量的4.38%；韩国是蒙古国第六大贸易伙伴。

2.东北亚五国的直接投资总量稳中有升。近5年来，东北亚五国间的直接投资总量偏少，但是呈稳步增长态势。2018年，日本对华直接投资数量达828家，同比增长40%。2019 年，中国在俄罗斯经济最活跃的投资者排名中位居第二。2019年中国实际使用韩资55.4 亿美元，同比增长18.7%。2019 年，中国对蒙古投资2.7 亿美元，同比增长132.0%。2019 年，蒙古对中国投资79万美元，同比增长92.7%。中国成为对蒙古投资最大的国家，占蒙古引入外资总量的40%。

（三）东北亚五国货币汇率近10年表现出动态稳定的走势

经济贸易联系日益增强，必然带动各国货币汇率之间的联系。东北亚五国汇率变动特征如图2所示，2009 年以来，东北亚各国汇率变化各不相同。以2014年为拐点，人民币在2014年之前不断升值，之后不断贬值，2018年后小幅升值；日元在2012年之前升值，2012年之后开始贬值，2016年以后由波动趋于稳定；韩元在2009～2014 年经历小幅升值，之后处于小幅波动中；蒙古图格里克和俄罗斯卢布在2010 年和2011年有小幅升值，此后均不断贬值，且有些年份贬值幅度较大。东北亚各国汇率的变化反映了各国货币价值的相对变化，人民币在近些年来有所升值，也推动了东北亚地区更多的货物往来和经贸交流使用人民币结算。东北亚各国的汇率保持着动态稳定和平衡，有利于东北亚各国更好地进行货币结算和金融合作。

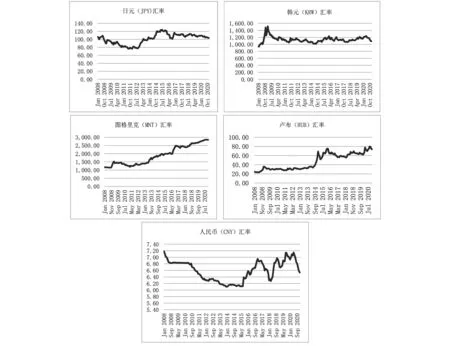
图2 2008～2020年东北亚五国货币汇率走势

四、东北五国货币汇率联动的实证分析

（一）模型设定

由于单个时间序列模型无法解决多元时间序列的问题，Sims（1980）提出向量自回归（VAR）模型，对于研究相互联系的时间序列的动态传递问题具有重要的意义。金融时间序列还需对波动率进行研究，对此，早期学者Engle（1982）和Bollerslev（1986）分别提出自回归条件异方差（ARCH）模型和广义自回归条件异方差（GARCH）模型。由于单变量ARCH 和GARCH 模型的使用只能考察单个市场的波动特征，为进一步研究不同市场间的波动关系，必须使用多元GARCH 模型。运用多元GARCH 模型考察某个市场价格发生波动时，既要考察该价格自身的变化，还要考察该价格对其他市场价格的联动，这通常被认为是价格波动的传导功能。Bauwens（2006）对一元GARCH模型进行直接扩展，首先提出VEC模型，后来又为了减少待估计参数提出对角VEC 模型，该模型的形式如公式（1）所示。

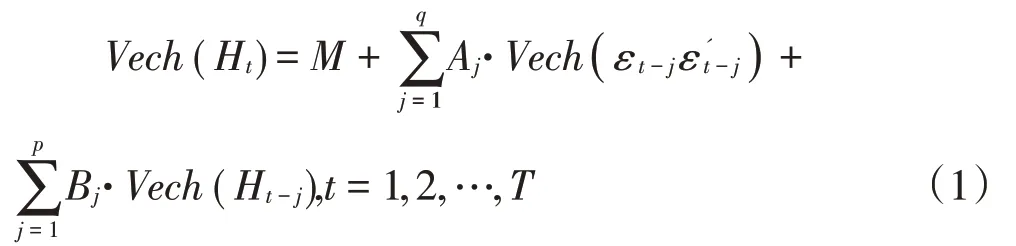
其中，Ht为n维的条件方差和协方差矩阵；εt-j为n 维随机扰动项列向量；Vech（）是误差修正算子，按列堆积下三角矩阵，堆积成维向量；M为维的方程截距项；Aj为维的ARCH 项参数方阵，是对角矩阵；Bj为维的GARCH项参数方阵，是对角矩阵。

但对角VEC 模型仍然存在VEC 模型固有的缺陷，即无法保证Ht的正定性，且在处理多维数据时，估计参数量依然非常巨大。对此，参考BEKK 模型，保证条件方差和协方差矩阵的正定性，BEKK 模型表述如公式（2）所示。

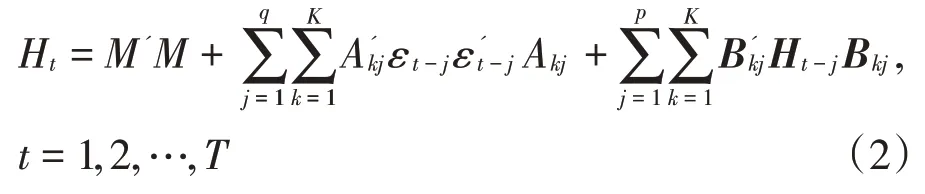
其中，Ht为n 维条件方差和协方差矩阵；εt-j为n维扰动项列向量；M 为n 维的方程截距项，是上三角阵；Akj为n 维的ARCH 项参数方阵；Bj为n 维的GARCH项参数方阵。

为了研究中国、日本、韩国、蒙古、俄罗斯五国之间的汇率联动性，本文将均值模型设定为VAR模型，一般来说GARCH（1，1）足够用来描述外汇市场的波动状况，且BEKK模型K一般取值为1，故本文的方差模型设定为GARCH（1，1）-BEKK 模型，如公式（3）、公式（4）所示。

均值方程：

方差方程：

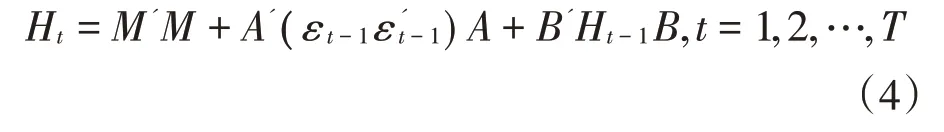
均值方程中，Y代表五个国家汇率时间序列的集合(y1、y2、y3、y4、y5)'；X 代表五个方程内生向量的集合；Δ代表五个参数向量集合(δ1、δ2、δ3、δ4、δ5)'；ε代表五个扰动项向量的集合(ε1、ε2、ε3、ε4、ε5)'。方差方程中，Ht是5×5 的方差协方差矩阵，代表各国汇率波动的方差和协方差；M是上三角矩阵；A的主对角线元素体现汇率波动的集中程度；B的主对角线元素体现汇率波动的持续程度；A 和B 的非对角线元素体现汇率之间的相互作用，即汇率的联动程度。

对于该模型，本文利用对数极大似然法估计参数，如公式（5）所示。

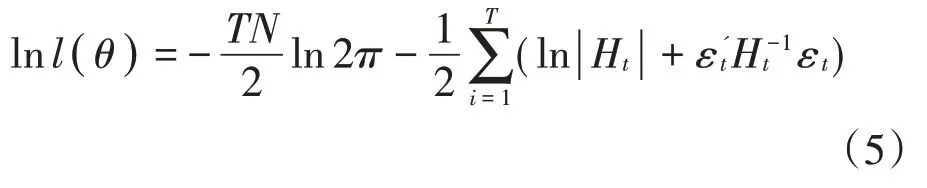
其中，θ表示要估计的参数，T为观测值数量，N为估计的变量数目（本文N=5），Ht表示汇率的方差协方差矩阵，εt表示残差向量，其服从条件正态分布。

检验均值方程系数能够判断各国货币汇率是否存在均值溢出，检验矩阵A 和B 中的系数是否为0 就能判断各国货币汇率是否存在波动溢出。对于波动溢出，本文提出以下假设。

假设1：i货币汇率对j货币汇率不存在波动溢出，即H0:aij=bij=0。

假设2：j货币汇率对i货币汇率不存在波动溢出，即H0:aji=bji=0。

（二）样本数据描述

本文使用东北亚五国货币兑美元的汇率数据，即分别为人民币（CNY）、日元（JPY）、韩元（KRW）、图格里克（MNT）、卢布（RUB）对美元的汇率。样本范围为2014 年2 月28 日至2019 年2 月26 日5 年的汇率日数据，数据来源于OANDA。对数据进行预处理，计算各货币汇率的日波动率表示为ln( )Pt-ln(Pt-1)，为了使估计结果更利于观察，将各货币汇率的日波动率同乘100，即Rt=100×[ln( Pt)-ln(Pt-1)]

表1 给出五种货币汇率日波动率的描述性统计量。从均值和标准差可以看出图格里克和卢布汇率的日波动率远高于人民币、日元和韩元汇率，卢布汇率波动最大，人民币汇率波动最小。从峰度和偏度可以看出五国汇率日波动率的分布具有“尖峰厚尾”的特征。本文利用EVIEWS 软件对样本数据进行Jacque-Bera 检验和ADF 检验，表1 的结果表明，五国货币汇率日波动率序列均不存在正态分布，且都为平稳时间序列。

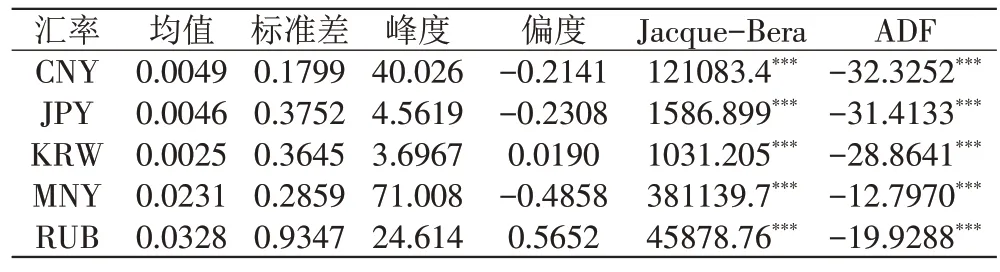
表1 2014～2019年东北亚五国货币汇率波动率描述性统计

（三）均值方程结果分析

本文首先对五国货币日波动率建立VAR 模型，综合LR、FPE、AIC、SC、HQ 准则的检验结果，确定VAR 模型的滞后阶数为2 阶，因此建立VAR（2）-GARCH（1，1）-BEKK（1）模型，模型估计结果通过Rats软件计算得到。

均值方程的估计结果如表2 和表3 所示，结果表明：t 时刻人民币汇率波动率除受自身滞后一期（t-1）、滞后二期（t-2）波动率影响外，还受滞后一期的日元和韩元波动率影响；t 时刻日元汇率波动率除受自身滞后一期和滞后二期的波动率影响外，还受滞后一期、滞后二期韩元汇率波动率影响；t时刻韩元汇率波动率除受自身滞后一期，滞后二期波动率影响外，还受滞后一期人民币、日元、卢布汇率波动率影响；t 时刻图格里克汇率波动率除受自身滞后一期、滞后二期波动率影响外，也受滞后二期卢布汇率波动率影响；t时刻卢布汇率波动率除受自身滞后一期、滞后二期波动率影响外，还受滞后一期日元汇率波动率影响。根据实证情况，可以总结为：人民币汇率和韩元汇率波动率存在双向均值溢出，日元汇率和韩元汇率波动率存在双向均值溢出，日元汇率对人民币汇率和卢布汇率波动率存在单向均值溢出，卢布汇率对韩元汇率和图格里克汇率存在单向均值溢出，图格里克汇率不存在对其他货币汇率波动率的单向均值溢出。由此可见，人民币、日元、韩元汇率之间的关系非常密切，图格里克汇率与其他货币汇率之间相互影响很小。

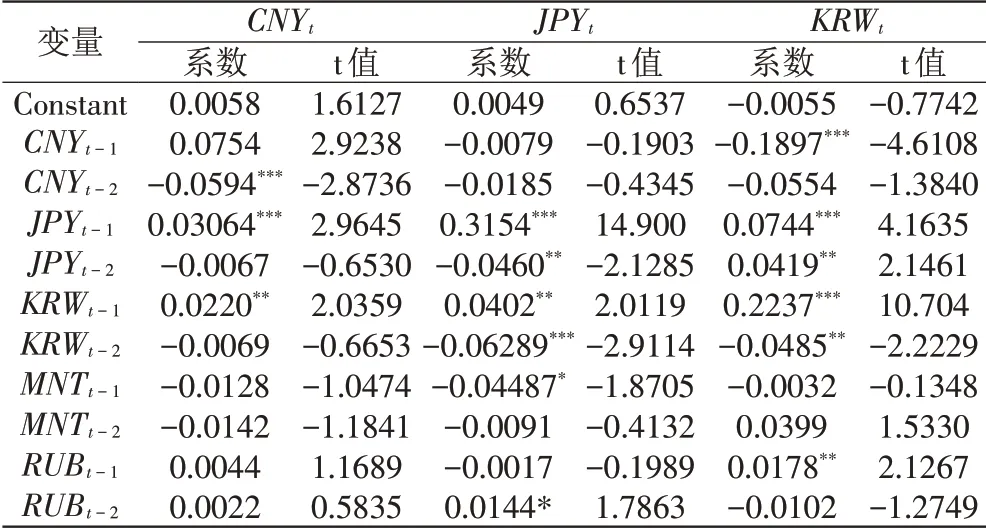
表2 人民币、日元、韩元汇率均值方程估计结果

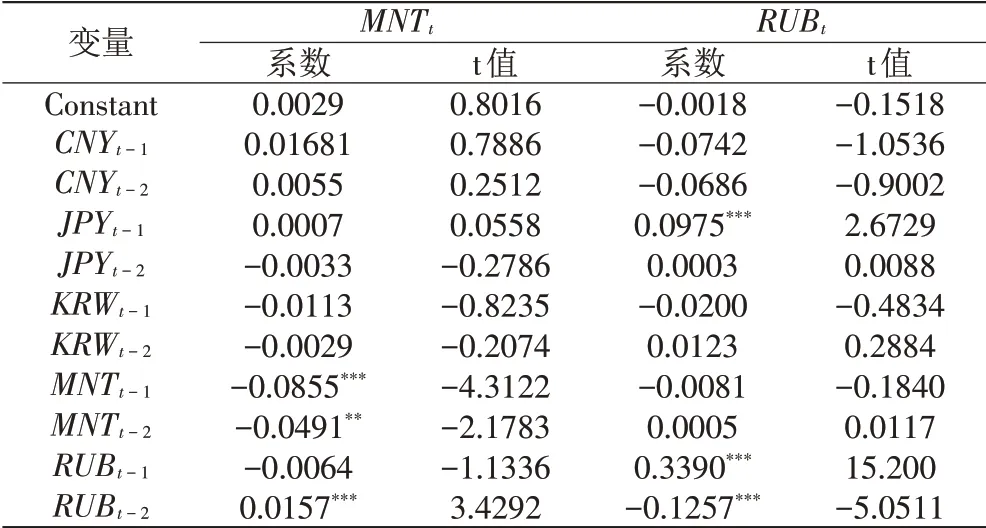
表3 图格里克、卢布汇率均值方程估计结果

人民币、日元、韩元汇率之间联动关系明显，三国之间贸易交往与合作比较频繁。卢布汇率对图格里克汇率的影响也离不开两国广泛开展的国际贸易往来。蒙古由于经济体量较小，虽然与中日俄存在密切的贸易关系，但对汇率的影响较小。

（四）方差方程结果分析

本文进一步用极大似然法估计VAR（2）-GARCH（1，1）-BEKK（1）模型，用BHHH 算法，估计结果如表4 和表5 所示，可以发现部分货币汇率波动率之间存在波动溢出。

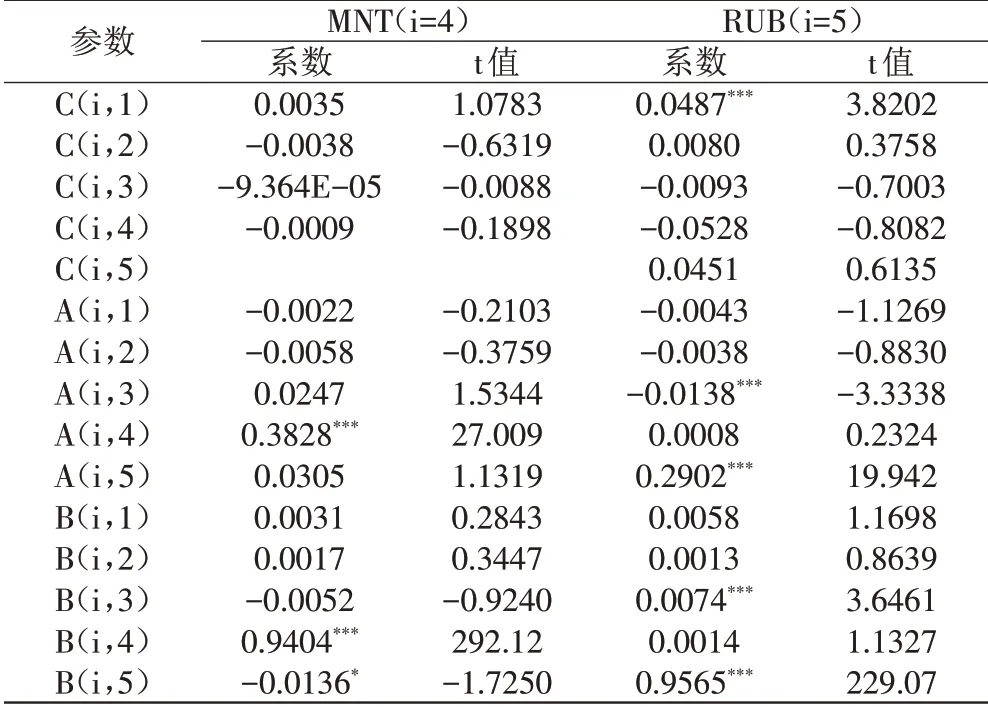
表5 图格里克、卢布汇率方差方程估计结果

为了更直观地判断各货币汇率波动率之间波动溢出的程度，对模型估计结果进行Wald检验，结果如表4所示，横轴所在货币汇率对纵轴所在货币汇率存在明显的波动溢出。可以得到，人民币汇率对日元、韩元、图格里克、卢布都具有汇率波动率的波动溢出表现，日元汇率对人民币汇率也具有汇率的波动溢出，韩元对人民币、日元、图格里克具有汇率的波动溢出，卢布对韩元具有汇率的波动溢出，其中人民币和日元、人民币和韩元具有双向波动溢出，其他货币汇率的波动溢出则为单向。

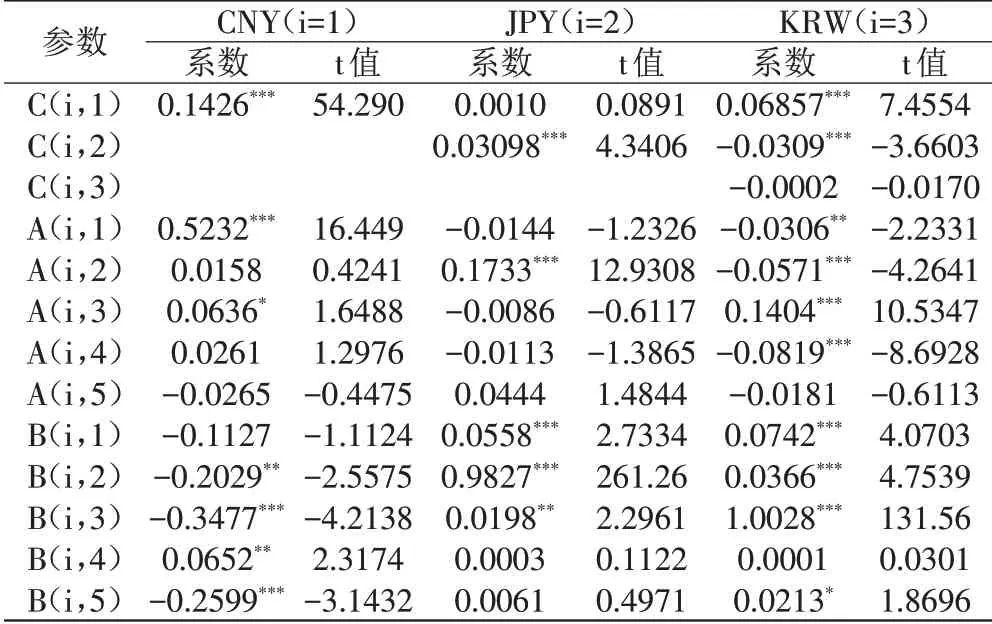
表4 人民币、日元、韩元汇率方差方程估计结果

人民币对东北亚其余国家的货币都存在波动溢出，这是因为中国经济体量大，是东北亚其他国家的第一大出口国，也是东北亚国家（除日本外）的第一大进口国。人民币和日元、人民币和韩元存在双向波动溢出，韩元对日元存在波动溢出效应，反映中日韩三国密切的贸易联系。

五、实证结论及政策建议

（一）实证结论

本文对东北亚五国货币汇率联动关系进行实证分析，基于2014 年2 月28 日至2019 年2 月26 日人民币、日元、韩元、图格里克、卢布的汇率日数据，运用VAR-MGARCH-BEKK模型进行研究，得到如下结论。

1.针对人民币、日元和韩元汇率。日元对人民币存在单向均值溢出，两者存在双向波动溢出；人民币和韩元存在双向的均值溢出和波动溢出；日元和韩元存在双向的均值溢出，韩元对日元存在单向波动溢出。可见东北亚国家中，中日韩三国汇率联系密切，任何一国货币汇率发生变动都会影响其他两国货币汇率。

2.针对图格里克汇率和其他货币汇率的关系。图格里克对东北亚其他国家货币都不存在均值溢出和波动溢出，其汇率变化对人民币、日元、韩元、卢布汇率基本没有影响。但图格里克会受到人民币和韩元的均值溢出和卢布的波动溢出的影响，这可能与蒙古和中国、韩国以及俄罗斯国际贸易联系较为紧密有关。

3.针对卢布汇率和其他货币汇率。卢布对韩元存在均值溢出和波动溢出，说明卢布汇率的变化能显著影响韩元汇率，卢布对图格里克存在波动溢出，表明俄罗斯与蒙古贸易联系较为紧密。此外，卢布受到人民币均值溢出和日元波动溢出的影响。

随着“一带一路”倡议的深入推进，未来东北亚区域经济贸易往来将更加频繁，以地缘为基础的东北亚区域经济合作也将加速推进，卢布、图格里克与人民币、日元和韩元五国货币的汇率联动机制将更为突出，均值溢出和波动溢出的程度将更为显著。

（二）对策及建议

1.稳步增加人民币与东北亚各国货币互换。上述实证分析可以看到，我国和东北亚各国之间的经济、贸易与货币联系日益增强，为在东北亚各国扩大人民币使用提供了环境和条件。我国中央银行目前与日本、韩国、俄罗斯和蒙古均签订货币互换协议，各国应在此基础上，进一步巩固协议关系，增强政治互信，加强多边合作，积极推进货币互换和货币合作进程。落实货币互换协议，推动货币互换实际使用，有助于推动人民币国际化进程，同时，也有利于规避各国贸易投资往来中的汇率风险。

2.加快政策性银行体系建设，促进东北亚货币合作。“一带一路”背景下，进一步促进亚投行和东北亚其他国家的基础设施建设，加强政策性银行，如亚洲开发银行等，以及商业银行的货币金融合作，提高人民币在东北亚区域的认可度，以中国在东北亚其他国家建立的银行分支机构为中介，进一步推进东北亚国家间的银行合作，提高货币流动性，更好地促进东北亚地区经济金融合作。

3.推动人民币在东北亚的区域化进程。根据各国实际，有序增加人民币在东北亚国家贸易往来中的计价结算规模，加大对东北亚国家跨境人民币政策产品的推介力度，努力消除人民币跨境使用障碍，鼓励和支持东北亚国家持有以人民币计价结算的资产，推动人民币东北亚区域化进程。