煤炭行业风险预控管理体系干预效应实证研究

法子薇，李新春

（中国矿业大学 经济与管理学院，江苏 徐州 221116）

我国煤炭行业长期处于“劳动强度高、从业危险高、事故发生率高”的状况[1]，近年来，煤炭行业每百万吨死亡率在逐年下降，但重特大安全事故仍时有发生，与世界主要产煤国家相比差距依然较大。在此背景下，国家煤监局组织神华集团和多所安全生产研究机构，耗时2年研发出了一套结合中国煤炭发展特色的安全管理体系—风险预控管理体系，目前已在全国的河南、陕西、山西、山东和新疆[2]等省份约500多个煤矿推行使用。体系建设之后，从每年的死亡人数和事故发生频率等安全状况指标数据来看，我国煤矿安全管理水平有一定程度的提高。然而，从国家督促各企业建设煤矿安全风险预控管理体系以来，对于全国煤矿安全记录的改善，该体系的具体贡献程度是多少，影响程度有多大，目前还未有相关研究。因此，将结合定量与定性分析，对因体系建设为煤矿安全管理水平带来的变化进行实证研究。

1 文献综述

随着“安全发展”理念的深入贯彻，煤炭安全管理研究已成为许多学者的重要研究课题。很多学者从政策分析的角度，指出煤矿安全管理体制存在诸多问题，如Thomson[3]对一些成功与失败的政策进行了评价，认为中国政府不愿让市场力量不受限制的运作是主要原因；李新娟[4]通过对比中美煤矿安全管理体制机制的特点，指出了中国煤矿安全管理体制存在的问题并给出了具体的应对措施；颜烨[5]梳理了自新中国成立后中国政府对煤矿安全生产监督管理的3个阶段，认为煤矿安全监管过程不仅需要政府，也需要公民社会的力量。此外，还有少量学者选择从定量的角度分析某项煤矿体制改革带来的实际影响，其中，白重恩[6]利用双重差分法检验了煤炭行业关井政策对乡镇煤矿安全生产的影响，并认为其在一定程度上导致了死亡率的显著上升；刘全龙[7]构建了时间序列模型以评估1999年煤矿安全监管体制改革的效应，实证结果显示这一改革有助于我国煤矿安全记录的长期改善。

从文献回顾的情况来看，现有研究已从不同的角度对中国煤矿安全管理的现状、方法和评价等方面进行了研究，且不同的角度之间正在融合，但是通过分析前人的研究，发现有关煤炭行业风险预控管理体系建设效果的定量研究却很少涉及。

2 干预模型构建

2.1 指标选取和数据来源

衡量煤矿安全生产管理水平的指标有很多，包括每年的受伤人数、死亡人数和财产损失等，但这些指标数据会因每年开采的原煤数量不同而上下波动，继而影响政策干预效应评价的客观性，因此选用每百万吨死亡率这一安全数据作为研究对象，可以综合且全面地反映不同政策对中国煤炭安全生产水平的干预程度；选取2000—2019年的样本数据作为实证研究区间，所有数据均来自《中国煤炭工业统计年鉴》，并以2011年作为风险预控管理体系干预的起点，通过分析该时间节点之后政策带来的具体干预值，从数据挖掘角度分析推行该体系对我国煤炭行业管理水平的有效性程度。

2.2 干预分析模型

干预分析模型[8]由国外学者Box和Tiao于1975年提出，干预模型最初来源于工业生产过程中的传递函数模型[9]，干预分析模型的作用机制如图1。

图1 干预分析模型作用机制图Fig.1 Mechanism diagram of intervention analysis model

在此传递函数模型中，X为量化系统输入的水平，Y为系统输出的水平，当某一时刻X的水平发生了变化，由于时间滞后效应，Y的输出值并不会立即改变，而是随着时间的变化逐渐达到一种新的均衡状态，这种描述系统之间动态影响的模型被称为传递函数模型。但系统实际作用时，除输入变量X之外，其他的影响也会一定程度上干扰Y的输出效果，因此将此类干扰定义为噪声N（假设N与X的水平独立），干预分析模型正是在识别传递函数模型和噪声模型的基础上，将2种模型组合起来，用以分析干预事件对时间序列Y的影响程度。

根据干预事件的持续时间，可将干预变量分为脉冲式干预变量PtT和持续性干预变量StT（t为时间变量，T为干预事件介入的时间)，具体可表示为：

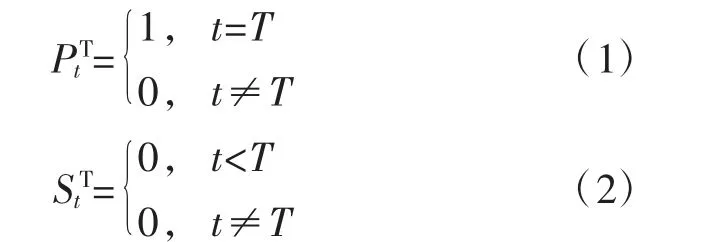
由于分析的是风险预控管理体系建设带来的有效性程度，而体系的建设并不是一蹴而就的，企业需要一定时间建立和完善，可认为干预效果是逐渐增加的，即干预类型为阶跃式[10]，传递函数Zt模型为：

式中：ω0为干预因素初期的干预效果；δ为此后每期的干预变化速率；B为后移算子。

而对于噪声模型部分Nt而言，决定采用灰色系统方法，利用数据本身寻找数据间的规律，而不是找概率分布、统计规律，即使有效样本观测值过少对其预测结果也无太大影响。整体干预分析模型Yt为：

2.3 干预分析具体步骤

干预分析步骤为：①利用政策干预之前的时间序列，建立噪声部分Nt的灰色模型，利用此模型进行外推预测，得到干预未介入时序列的原始数值X′t；②用干预后序列的实际数值减去预测值，得到干预事件的初步影响值Zt，求得事先根据干预性质决定的传递函数模型中的各参数；③根据传递函数模型求出干预影响的拟合值，再用实际观察值减去拟合值，得到消除了干预影响的净化序列；④结合对净化序列的数据趋势图建立合适的时间序列模型，并拟合干预事件后各年份的数值，最后用实际值减去拟合值，得到修正后政策干预带来的实际影响值。

3 实证分析

3.1 干预前的GM（1，1）灰色模型

利用2000—2010年煤炭行业每百万吨死亡率的原始数据Xt，按照灰色系统理论的建模步骤，建立煤炭行业风险预控管理体系干预效果的灰色模型：

式中：k为数据值，k＝1，2，3，…，n。

分别对该模型进行残差检验、关联度检验和后验差检验，得到该模型的平均相对残差值为0.096 8，在α=0.1水平上勉强合格；关联度为0.619＞0.600，表明模型值曲线与建模序列曲线的相似程度较高；方差比C为0.091 5＜0.350 0，且小误差概率P=1.00＞0.95，故模型比较合适。比较上述3个检验结果，关联度检验和后验差检验的结果为优，只有残差检验的结果为勉强合格，因此对原模型进行残差均值修正，在模型预测值X(0)（k）的基础上加上残差均值E，以提高新模型的预测精度。修正前后模型的预测值见表1。

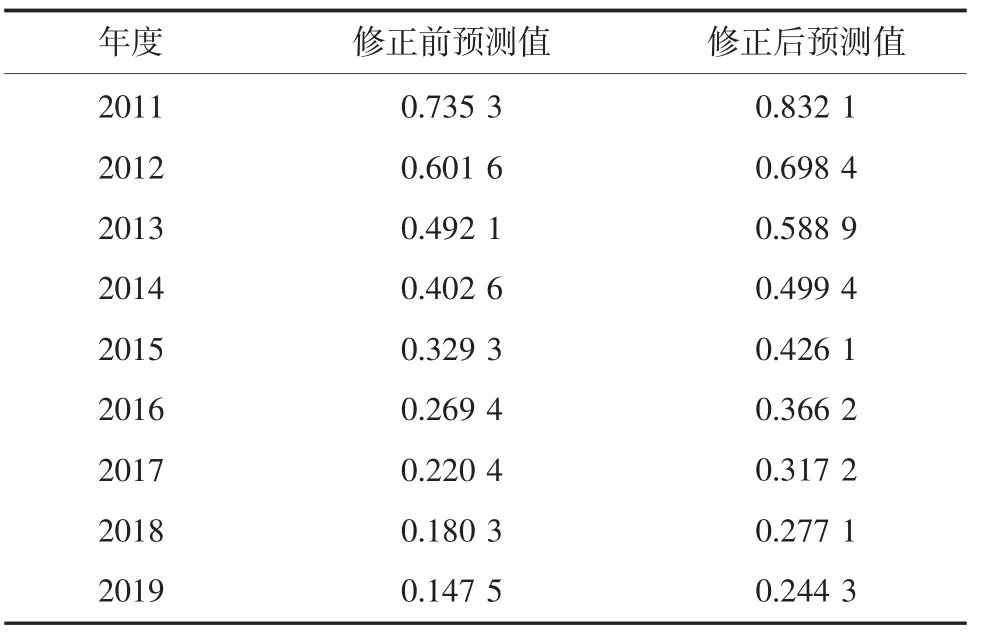
表1 GM（1，1）模型预测值Table 1 Predicted values of GM（1，1）model

3.2 干预模型

考虑到每百万吨死亡率这一安全指标数据在2011年之后的绝对值变化幅度已较小，此时每一期变化差异的意义不同，单从数据本身实际值和预测值的差值来评估干预效应并不客观，可通过计算数据每一期的变动百分比来分析政策的干预效应，因此将实际数据和修正后的预测数据分别取对数，利用二者差值作为衡量干预效果的初步干预值，根据已确定的干预模型具体形式，求得模型中的各参数，干预模型参数输出结果见表2。

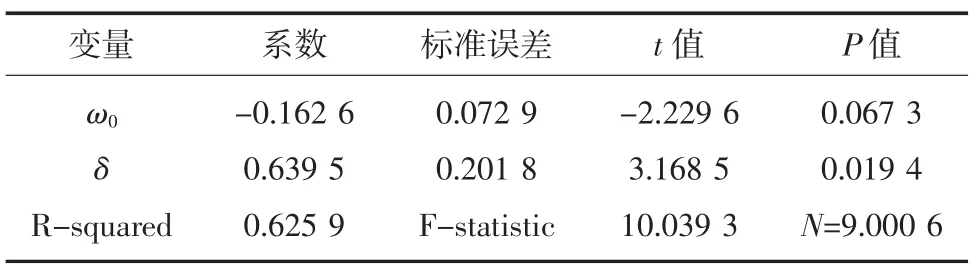
表2 干预模型参数输出结果Table 2 Output results of intervention model parameters

具体干预模型为：

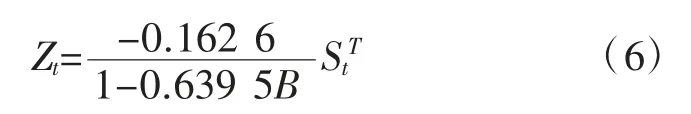
通过该模型可知在风险预控管理体系建设初期，煤炭行业每百万吨死亡率下降幅度约为16.26%，在接下来的时间内，按照模型所示，体系建设的干预效果会持续增加，每一期的百万吨死亡率下降百分比约增加10.40%（ω0×δ），长期内最终可使百万吨死亡率下降约45.10%（ω0/（1－δ）），但这些数值只是根据干预模型初步推断的结果，最终的干预效应值还需用净化后的时间序列模型进行修正得到。

3.3 净化后的时间序列模型

根据上述传递函数模型求出干预影响的拟合值序列g′t，则净化序列yt可由干预后的实际值减去干预影响的拟合值得到，具体表示为：

由于净化后的时间序列yt具有明显的线性趋势，因此建立相应线性回归模型对其进行拟合，得到线性模型：

其中R2=0.981 0，F=930.146 0，P=0，表明模型拟合效果较好。计算yt于2011—2019年的拟合值，最后利用实际值减去回归拟合值，风险预控管理体系建设对百万吨死亡率的干预影响见表3。

表3 风险预控管理体系对百万吨死亡率的干预影响Table 3 Intervention effect of risk precontrol management system on mortality of milliontons %

3.4 讨论分析

煤炭安全风险预控管理体系的建设对我国安全数据的干预影响是逐渐开始且持续下去的，并且随着企业对风险预控管理体系的深入学习和进一步完善，政策干预的效果越来越明显，从初步干预影响值和最终干预影响值来看，2017年为风险预控管理体系建设对我国煤炭行业安全状况改善力度最大的一年。但值得注意的是，2017年之后，体系建设的干预效应有微弱的下降趋势，这种趋势在最终干预影响中更为明显，且干预模型的拟合优度不是很好。

造成这种现象的原因主要有3点：①企业员工执行力度不够，随着时间的推移，员工可能会出现意识上的“松懈”，即在有规定和标准的前提条件下，执行力度慢慢减弱；②照搬现有体系，并未充分结合自身安全生产的现状；③缺乏对体系实施有效性的评估和提升研究，体系得不到改善，问题得不到解决，安全隐患慢慢累积，安全事故发生的可能性极大地提高，企业整体的安全管理效率反倒被制约。

结合上述分析，认为政府首先应强化实施力度，进一步完善督查审核体系；企业内部也应重视安全管理责任的落实，确保每个安全生产环节都有专人负责；同时结合自身生产情况，建设企业特色安全风险预控管理体系；最后定期开展风险预控管理体系有效性评估工作，在系统化管理的基础上，建立一套科学的安全管理有效性评价体系。

4 结语

建立干预分析模型，对我国煤炭行业风险预控管理体系的干预效果进行了实证研究。整体来看，该体系显著的提高了我国煤炭行业的安全管理水平，但近几年其干预效果略有下滑，可能是企业内部员工执行力度不够、体系建设缺乏自身特色或体系效果的评估与提升工作不到位所致。基于灰色系统和传递函数的干预模型，实现了对体系贡献程度的定量分析，同时提高体系评价的客观性。