基于SSA-RBF 网络的日光温室温湿度预测模型研究

张永芳，王 芳

（1.河北农业大学 信息科学与技术学院/河北省农业大数据重点实验室，河北 保定 071000）

日光温室通常是指温室内的热量来源主要是靠太阳辐射的温室，由于其取材方便、造价低、保温性强、不加温也可在冬季进行作物生产等特性，逐渐成为我国北方普遍采用的温室类型。通过建立日光温室温湿度模型，综合各个环境因子变化规律，有效预测日光温室内温湿度的变化，并以此为依据进行温室的调节控制，可以帮助日光温室内的作物获得良好的生长环境，降低病害发生几率，从而实现早熟、优质和高产，获得更高的经济效益，无论在温室设计和环境控制中都具有一定的现实意义。

日光温室温湿度模型涉及多个环境因子，具有非线性、时变、耦合、滞后等特性［1-3］，模型主要分为2 类：基于流体动力学和能量平衡的机理模型以及基于系统辨识方法的辨识模型。尽管机理模型可以解释系统本质，与实际过程吻合程度较高，但是，这类模型存在结构复杂、测量仪器昂贵、不易推广、参数时变因素多且部分参数只能凭经验获得［4］等缺点，一般较少在实际中使用［5］。辨识模型往往不需要关心具体的物理过程或数学模型，结构相对简单，易操作，预测曲线拟合度较好，不仅可以提高研究效率，减少成本，而且也更方便对温室环境控制系统进行控制。

在辨识模型方面，国内外学者已进行了很多探索，不断改进创新。早在2012 年C.X.Zhu 等［6］就提出了采用误差反向传播神经网络建立温室湿度预测模型；同年，郭正昊［7］提出利用支持向量机的方法建立土壤湿度预测模型。但由于误差反向传播神经网络学习速度较慢、网络训练失败的可能性较大等缺点，一些学者开始将目光转移到径向基神经网络，通过算法的优化逐渐提高其预测效果。2014 年许童羽等［8］通过分析比较误差反向传播和径向基神经网络，选择径向基网络作为预测网络，并采用高斯径向基函数作为网络激活函数，提出了1 种适用于北方日光温室空气相对湿度环境因子的模拟预测模型。2017 年Castaneda-Miranda,A 等［9］提出利用LM算法训练神经网络对温室温湿度建立预测模型，实现了墨西哥中部温室的智能霜冻控制；同年S.Xia等［10］提出了1 种基于PSO-RBF 神经网络的温室温度长期预测模型，将最大相对误差控制在1.5%以内；2018 年Youjun Yue 等［11］利用列文伯格—马夸尔特算法优化径向基网络，提出基于改进的LM-RBF 神经网络的温室温湿度预测模型，成功指导了温室温湿度控制；2019 年岳有军［12］等人进一步提出基于PSO-LM-RBF 的温室温湿度预测模型，提高了预测精度。

本研究在前人研究基础上，采用径向基网络作为预测网络，利用SSA 算法进行优化，用优化后的SSA-RBF 模型对日光温室温湿度进行仿真研究，进一步提高RBF 神经网络模型的预测精度，为接下来温室控制系统提供技术支持，在减少日光温室内对作物不利的环境因素、保障日光温室生产效益等方面具有重要意义。

1 数据的采集与处理

为研究日光温室温湿度模型，选取河北省沧州市青县某日光温室作为实验温室。该温室位于东经116°49'24"，北纬38°36'47"，南北跨度8 m，东西长85 m，高度约4.5 m，下挖深度0.5 m，前坡倾角30°，后坡仰角40°，室外设有保温被及卷帘机，室内设有通风装置和滴水灌溉装置，属于典型的北方日光温室。图1 是试验日光温室侧面示意图。

图1 试验温室示意图Fig.1 Schematic diagram of test greenhouse

日光温室温湿度模型涉及多个影响因子，作物光合作用及蒸腾作用、灌溉状况、室内温度、通风情况等因素都会对温室内温湿度造成影响。温室外部气象环境因素会在一定程度上影响温室内温湿度的变化。信志红等［13］通过对不同时段、不同天气条件下外部气象环境的温室内温湿度变化进行研究，发现日光温室具有良好的保温与保湿特性，温室内的温度和湿度的变化趋势同室外天气状况、气象条件等因素有着较为明显的相关性。具体表现为：总体上，温室内外湿度变化趋势呈正相关。在自然通风或强制通风情况下，室内外湿度变化趋势差距减小，呈明显的正相关；但在温室密闭时，相对湿度受外界环境因素影响较小，室内湿度大且相对维持稳定。综上，由于研究温室为日光温室，没有加温设备，且绝大部分时间为密闭保温状态，保温主要是依靠外设的保温被（被子卷起时散热放下时保温），通风依靠保温被下的塑料膜和内设窗户进行（塑料膜撑开和窗户关闭都可以减少通风），但通风时间相对较少，室内空气水分主要来源为作物生理作用、土壤蒸发和内设滴灌设备（滴灌设备打开增加空气湿度）。因此选取室外温度、室外湿度、光照强度、土壤湿度、保温被状态、塑料膜状态、窗户状态、滴灌设备状态作为输入，温室内温度和温室内湿度作为输出，其中室内外温湿度、光照强度、土壤湿度分别使用温湿度传感器、光照度传感器、土壤湿度传感器测量，采集设备选用HSTL-102WS温湿度传感器、HSTL-GZD 光照度传感器、HSTL-102STRWS 土壤湿度传感器等，保温被状态、塑料膜状态、窗户状态、滴灌设备状态用0 和1 分别代表关闭和打开。选择600 组样本，随机取其中70%作为训练集，剩余30%为测试集。

为提高模型的收敛速度和精度，在实验前将采集到的数据进行归一化处理。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。本文采取min-max 标准化即Min-Max Normalization 方法，也称为离差标准化，是对原始数据的线性变换，使得结果映射到0 ～1 之间。设minA 和maxA 分别是属性A 的最小值和最大值，将A 的1 个原始值x通过最大-最小标准化映射到区间［0,1］的值x'，那么公式如下所示：

2 构建方法及选择

2.1 径向基网络

径向基（Radial Basis Function）网络是20 世纪80 年代末提出的1 种单隐层、以函数逼近为基础的前馈神经网络。径向基网络可以解决BP 网络的局部极小值问题，且训练时间更短，对函数的逼近较优，可以以任意精度逼近任意连续函数。

径向基网络是1 个三层的网络，其中包括输入、隐含、输出3 层，第1 层为输入层，由信号源节点组成，仅起到数据信息的传递作用，对输入信息不做任何变换；第2 层为隐含层，对输入信息进行空间映射变换；第3 层为输出层，是对输入模式做出响应。总的来说，径向基网络就是用径向基函数作为隐单元的“基”，构成隐含层空间。隐含层对输入向量进行变换，将低维空间的模式变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。径向基函数如下所示：

其中，μt为中心点，σt为径基宽度。径基宽度决定了径向基函数下降的快慢。图2 是本文径向基网络的结构图，输入层包含8 个输入向量，其中x1、x2、x3、x4、x5、x6、x7、x8分别对应室外温度、室外湿度、光照强度、土壤湿度、保温被状态、塑料膜状态、窗户状态、滴灌设备状态，输出层共2个输出向量，其中Y1代表日光温室室内温度，Y2代表日光温室室内湿度。

图2 RBF 网络结构图Fig.2 Schematic diagram of RBF network

2.2 麻雀搜索算法

麻雀搜索算法（Sparrow Search Algorithm）［14］是2020 年由Jiankai Xue 和Bo Shen 根据麻雀觅食并逃避捕食者的行为而提出的1 种最新的群智能优化算法，算法主要模拟了麻雀群觅食的过程。麻雀群觅食过程也是发现者-跟随者模型的1 种，同时还叠加了侦查预警机制。麻雀中找到食物较好的个体作为发现者，其他个体作为跟随者，同时种群中选取一定比例的个体进行侦查预警，如果发现危险则放弃食物，安全第一。麻雀搜索算法的具体实现其实和人工蜂群算法非常相似，基本结构几乎一致，但是搜索算法有一定的差异，可以说是1 种人工蜂群算法的改进算法。该算法虽然全局搜索能力较弱且跳出局部最优的操作较弱，但其局部搜索能力极强，收敛速度较快［15］。整体过程如图3 所示：

图3 麻雀优化算法过程图Fig.3 Process chart of sparrow optimization algorithm

SSA 算法的具体求解过程：

（1）更新发现者的位置

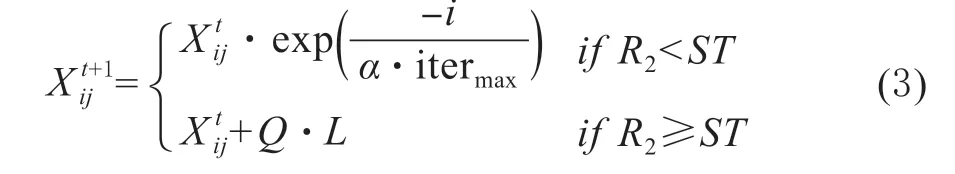
其中，t代表当前迭代数，itermax是1 个常数，表示最大的迭代次数。Xij表示第i个麻雀在第j维中的位置信息。α ∈(0,1］是1 个随机数。R2(R2∈［0,1］) 和ST(ST∈［0.5,1］) 分别表示预警值和安全值。Q是服从正态分布的随机数。L表示1 个1×d的矩阵，其中该矩阵内每个元素全部为1。当R2＜ST时，这意味着此时的觅食环境周围没有捕食者，发现者可以执行广泛的搜索操作。当R2≥ST，这表示种群中的一些麻雀已经发现了捕食者，并向种群中其它麻雀发出了警报，此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。

（2）更新预警者的位置

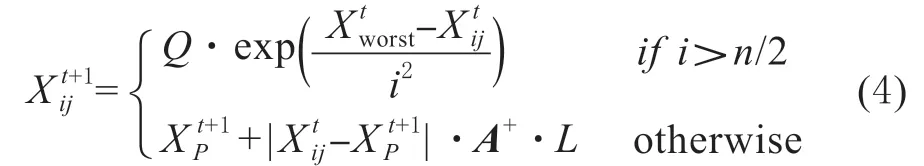
其中，XP是目前发现者所占据的最优位置，Xworst则表示当前全局最差的位置。A表示一个1×d的矩阵，其中每个元素随机赋值为1 或-1，并且A+=AT(AAT)-1。当i＞n/2 时，这表明，适应度值较低的第i个加入者没有获得食物，处于十分饥饿的状态，此时需要飞往其它地方觅食，以获得更多的能量。

（3）侦察预警行为

在麻雀觅食的同时它们中的部分会负责警戒，当危险靠近时，他们会放弃当前的食物，即无论该麻雀是发现者还是跟随者，都将放弃当前的食物而移动到1 个新的位置。每代将从种群中随机选择SD个个体进行预警行为。

当整个麻雀种群受到捕食者威胁时或者意识到危险时，会进行反捕食行为：处在种群外围的麻雀极其容易受到捕食者的攻击，需要不断地调整位置以此来获得更好的位置。与此同时，处在种群中心的麻雀会去接近它们相邻的同伴，这样就可以尽量减少它们的危险区域。

其位置更新公式如下：

其中，其中Xbest是当前的全局最优位置。β作为步长控制参数，是服从均值为0，方差为1 的正态分布的随机数。K∈［-1,1］是1 个随机数，fi则是当前麻雀个体的适应度值。fg和fw分别是当前全局最佳和最差的适应度值。ε是最小的常数，以避免分母出现零。

为简单起见，当fi＞fg表示此时的麻雀正处于种群的边缘，极其容易受到捕食者的攻击。fi=fg时，这表明处于种群中间的麻雀意识到了危险，需要靠近其它的麻雀以此尽量减少它们被捕食的风险。K表示麻雀移动的方向同时也是步长控制参数。

3 基于麻雀搜索算法的径向基网络

在日光温室温湿度预测方面径向基网络优势明显，但径向基网络使用的是1 个局部的激活函数。即在中心点附近有最大的反应，越接近中心点则反应最大，远离反应则成指数递减，就相当于每个神经元都对应不同的感知域，能够逼近任意非线性的函数。因此RBF 网络中所用的非线性函数的形式对网络性能的影响并不是至关重要的，关键因素是基函数中心的选取,中心选取不当构造出来的RBF 网络的性能一般不能令人满意。例如，某些中心靠的太近,会产生近似线性相关，从而带来数值上的病变条件。由于RBF 网络中心选取是该网络预测效果的重要影响因素,为了更好地预测日光温室温湿度，本文将利用上述提到的麻雀优化算法优化径向基网络中心点的选择。

常规径向基网络利用K-means 来选择中心点，但K-means 方法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销也很大。但日光温室温湿度的预测需要大量的样本进行分析，利用K-means选择中心点无疑会带来较大的开销，异常情况存在的可能性也使麻雀搜索算法的存在更加必要。因此本文将利用麻雀优化算法对构建的径向基神经网络的初始聚类中心进行优化，该方法利用进化策略在解空间内对选择路径进行多点随机搜索并找到最优选路径。由于进化策略的随机性所有选择路径都有被搜索的可能使它有可能找到全局最优解。将该方法用于RBF 中心的选取上具有以下特点：1、把RBF 网的结构设计问题归结为寻找最优选择路径问题，然后采用进化策略进行寻找，从而可得到最优的隐层节点数和数据中心。2、该方法简单易行，且能设计出满足精度的最小结构的RBF 网络。

麻雀搜索算法通过各麻雀个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度，径向基网络具有局部逼近性能和最佳逼近性能，利用麻雀搜索算法优化径向基神经网络，不仅可以增加径向基网络的鲁棒性、泛化性，还可以增加径向基网络的学习能力和收敛速度，便于更好地对日光温室温湿度进行预测。

4 模型的建立与结果

基于SSA-RBF 网络的日光温室温湿度预测模型具体建立步骤如下：（1）根据分析确定输入层的8个节点和输出层的2 个节点。（2）将收集到的数据根据第二部分所提到的min-max 标准化方程进行归一化处理。（3）随机选取全部数据的70%作为训练样本，其余30%作为测试样本。（4）按照第三部分所提到的构建方法进行神经网络的构建。（5）利用3.2 节介绍的麻雀搜索算法对构建的径向基神经网络的初始聚类中心进行优化，建立基于SSARBF 的日光温室温湿度预测模型。其中，麻雀搜索算法出于对最优解和运行时间的考虑选择种群数为40，为了增加可预期性和稳定性选择最大迭代次数为500 次，发现者占总规模的比例为20%。将所有归一化的数据代入搭建好的预测模型中分别作为输入因子和输出因子，通过Matlab 进行仿真验证，利用基于RBF 网络的日光温室温湿度预测模型作为对照模型，仿真结果如图4 到图5 所示：

（1）对照组——常规径向基神经网络仿真预测结果：

图4 RBF 湿度预测结果对比图Fig.4 Comparison chart of RBF humidity prediction results

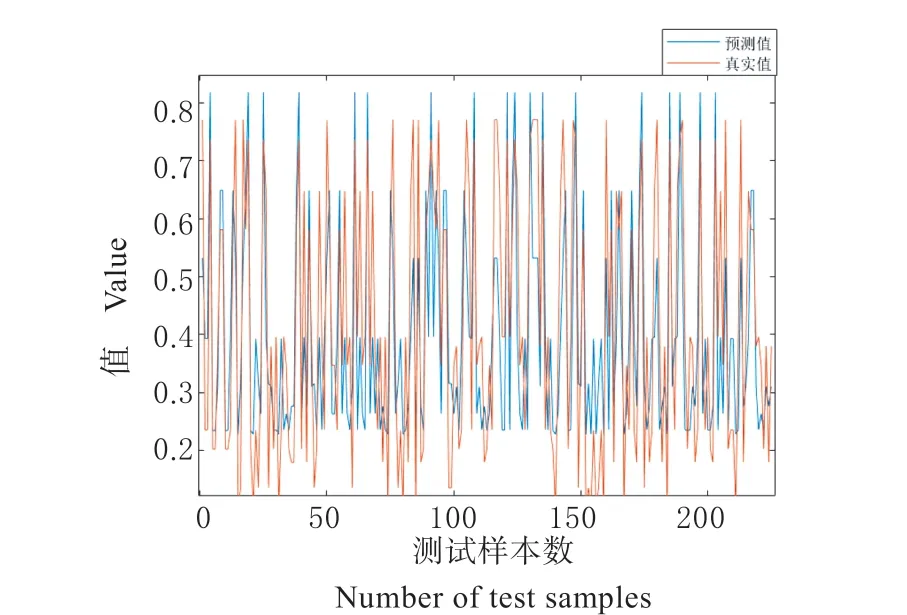
图5 RBF 温度预测结果对比图Fig.5 Comparison chart of RBF temperature prediction results

（2）基于麻雀搜索算法的径向基神经网络仿真结果（见图6 到图7）：

图6 SSA-RBF 湿度预测结果对比图Fig.6 Comparison chart of SSA-RBF humidity prediction results

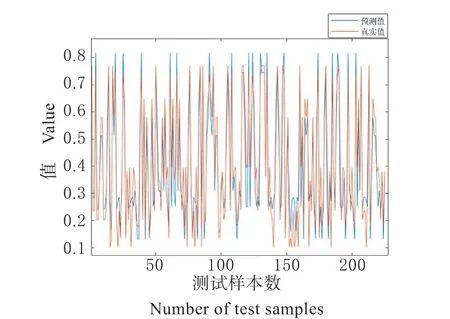
图7 SSA-RBF 温度预测结果对比图Fig.7 Comparison chart of SSA-RBF temperature prediction results

为了更好地衡量预测的准确性，本文将通过根平均误差RMSE（数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10，范围［0,+∞］，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大）、平均绝对误差MAE（当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大）、平均绝对百分误差MAPE（该指标体现出与原始数据相比较的过程，较为公正客观）、R-square 决定系数（此处的R即相关系数，相关系数的平方就是决定系数）以及相关系数（用来衡量2 个变量之间的相关性大小）进行深入地分析评估，计算结果如下表1 所示：

表1 计算结果Table 1 Calculation results

通过以上仿真结果可以看出，使用麻雀搜索算法能在一定程度上优化RBF 网络建模，能够有效提高该系统的预测精度，同时系统的运行速度也得到相应的提高。使用麻雀搜索算法对径向基网络进行优化后各个数据相对于未优化的常规径向基网络都有了不同程度上的改善，由此可以看出采用麻雀搜索算法优化径向基神经网络可以更好地满足日光温室温湿度预测的要求，而且能有效地在实际生产中对日光温室温湿度进行预测，为温室环境控制器设计提供理论支撑。

5 结论

本课题组基于RBF 神经网络并结合了麻雀搜索算法对日光温室温湿度预测模型展开了研究。同时，通过MATLAB 2019a 软件平台，利用采集到的日光温室环境数据进行了预测仿真实验，相比未被优化的常规径向基网络预测结果而言，基于麻雀搜索算法的径向基神经网络对日光温室温湿度的预测结果更好，验证了麻雀搜索算法优化日光温室温湿度径向基网络模型的可行性，可供进一步的研究和实际应用。