基于机器学习的粮食产量预测模型研究

贾梦琦，蔡振江，胡 建，陈浩松，王 楠，刘红星

（1. 河北农业大学 机电工程学院，河北 保定 071000； 2. 河北农业大学 经济管理学院，河北 保定 071000；3. 中央农业广播学校保定分校，河北 保定 071000）

河北省是我国粮食主产区之一［1］，保定市粮食年产量基本占到河北省的1/5。近年来，保障粮食安全在促进国家和社会经济发展方面发挥着重要作用，粮食产量的预测成为了1 个重要的研究课题。由于粮食产量通常受到气象、土地、人类利用活动、制度等因素影响［2-6］，对于粮食产量的准确预测十分困难。因此，利用有针对性的模型和方法预测粮食产量的发展趋势具有很强的现实意义。

近年来，众多学者为了准确掌握和预测全国各地的粮食产量进行了大量的研究。王晓玲，孔思琪［7］利用灰色关联度分析黑龙江省粮食产量的影响因素。赵金霞［8］针对粮食产量影响因素利用层次分析法，得出了粮食增量受社会经济因素影响较大。戎陆庆等［9］采用灰色关联(GRA)方法和BP 神经网络模型对广西粮食产量进行了预测，将预测的相对误差降低到1.5%以下。王春雨［10］利用遥感技术分析了孟印缅3 个地区的气候因素和人类活动因素对粮食产量的影响，提出了相应的管理政策。武单［11］依据计量地理学理论，针对湖南省粮食产量的多个影响因素进行研究，分析得出湖南省粮食产量的主要影响因素是农业机械总动力和化肥施用量的结论。阙斐艳［12］分析湖南省粮食产量变化与农村劳动力投入的相关性发现，湖南省农村劳动力转移对粮食产量没有显著影响。李礼连等［13］对1978—2009 年湖南省粮食产量波动进行分析认为，粮食产量的增加与粮食作物播种面积、化肥使用量和抗灾防灾财政投入相关性较大。

笔者认为，现有的预测方法对于数据量的依赖较大，在实际使用中不太方便。因此，需要找到能够准确预测小数据集的方法对粮食产量进行合理的预测。本研究采用ARIMA 模型、LSTM 模型以及ARIMAGRNN 组合模型对粮食产量进行预测，探究其预测效果，可为粮食产量的监测和控制提供依据。

1 研究数据与方法

1.1 数据来源

本文采用的样本数据为1996—2017 年保定市粮食产量相关数据，样本数据来源于《保定市经济统计年鉴》。收集1996—2017 年保定市粮食产量及影响因子用于模型构建及检验。

1.2 统计学分析

采用Excel 工作表建立保定市粮食产量及粮食产量影响因子数据库，运用Python 软件进行ARIMA 模型、LSTM 模型以及ARIMA-GRNN 组合模型的构建和预测。

1.3 ARIMA 模型的构建

ARIMA 模型是时间序列分析模型中较为常用的1 种，主要用于发现和探索数据随时间变化的规律［14］。1970 年，Box 和Jenkins 基于时间序列分析发表了差分自回归滑动平均模型(Autoregressive Integrated Moving Average model)，简称ARIMA 模型［15-16］。

ARIMA(p,d,q)模型中对于p、d、q的确定最为关键，AR 为自回归模型，p为自回归平均阶数；p阶自回归过程的定义为：

yt为当前值，μ为常数项，p为自回归模型的阶数，γi为自相关系数，εt为误差。

MA 为滑动平均模型，q为滑动平均阶数［17］；q阶自回归过程的定义为：

yt为当前值，μ为常数项，q为滑动平均模型的阶数，θi为自相关系数，εt-i为误差。

d为将非平稳时间序列变为平稳序列的差分运算次数。

ARIMA 建模过程具体分为5 个步骤：特征分析、模型定阶、模型参数优化、模型验证和模型预测，如图1 所示。

（1）特征分析。ARIMA 模型最关键的是需要将非平稳时间序列变为平稳时间序列。平稳时间序列需要均值和方差不发生明显的变化，方差越大，数据波动越明显。方差计算公式如下：

σ2为总体方差，X为变量，μ为总体均值，N为总体个数。方差次数即ARIMA（p,d,q）中d的阶数。

（2）模型识别。ARIMA(p,d,q)模型中p、q的选择，根据自相关函数ACF (Auto correlation function)和偏自相关函数PACF(Partial autocorrelation function)图来确定，其中p和q的取值不唯一。ACF 自相关函数反映了数据在不同时间序列之间的相关性，自相关函数ACF 公式如下：

其中，ρk为自相关函数，t为滞后时间，k为滞后期数；若k=3 时，不仅描述了yt和yt-3 之间的相关性，还描述了yt-1 和yt-2 之间的相关性。自相关函数ACF(k)的取值范围为［-1,1］，1 为正相关，-1为负相关，0 为不相关。

偏自相关函数PACF 描述的是预测值与实际值之间的线性相关性。当k=3 时，描述的是yt和yt-3之间的相关性，剔除了yt-1 和yt-2 的影响。

（3）模型参数估计。ARIMA 模型选择参数时，赤池信息准则(AIC)可以弥补ACF 和PACF 定阶的主观性。AIC的定义为：

其中L为最大似然函数，N为数据个数，k为变量个数。参数的选择需运用赤池信息准则(AIC)进行比较择优，在同样本的模型估计中，AIC值越小模型越好，说明该模型虽然使用的参数较少但拟合度却足够。

（4）模型检验。若要对时间序列进行白噪声检验，需把非平稳序列经过n次差分运算变为平稳序列。若白噪声检验P＞0.05，证明该时间序列拟合效果良好。

（5）模型应用。运用上述得到的最优模型进行预测，将预测值与实际值进行对比，计算平均相对误差。

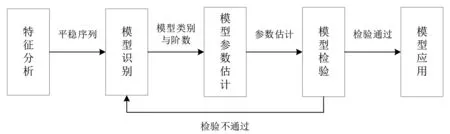
图1 ARIMA 建模过程示意图Fig. 1 Schematic diagram of ARIMA modeling process

1.4 ARIMA—GRNN 组合模型的构建

广义回归神经网络(GRNN)是在1991 年被Specht正式提出的基于非线性回归分析的前馈型神经网络模型。GRNN 针对较少的时间序列数据，具有良好的预测效果，且在处理非线性数据方面优于ARIMA 模型。通过建立ARIMA-GRNN 组合模型既能识别线性数据也能识别非线性数据，理论上可以提高模型的预测精度。ARIMA-GRNN 神经网络在粮食产量预测的运算中，主要有3 个步骤［18］：

（1）归一化处理：农业数据数量级复杂多样，需把数据归至［0,1］之间，避免因数据数量级差别较大导致GRNN 神经网络预测误差增大。归一化公式如下：

x为原始数据，xmin和xmax分别为原始数据的最小值、最大值，xi为归一化处理后的数据值。

（2）确定数据样本，包括输入样本、输出样本、训练样本和预测样本。本研究的输入样本为保定市1996—2014 年粮食产量ARIMA 模型的拟合值，输出样本为该时间段的实际值。

（3）构建GRNN 神经网络模型：在模型构建的过程中，需确定光滑因子spread这个参数。

2 结果与分析

2.1 ARIMA 模型的建立

2.1.1 保定市粮食产量时间序列分布 对保定市

1996—2017 年粮食产量（图2）数据进行单位根检验ADF，结果为ADF=0.025，证明该序列为非平稳序列。

图2 保定市1996—2017 年粮食产量Fig.2 Food production in Baoding city from 1996 to 2017

2.1.2 差分运算 由于时间序列为非平稳序列，需对其进行差分运算使之转换为平稳序列。将原序列进行2 阶差分后（图3），均值围绕0 不断波动，可以看出经过二阶差分的时间序列为平稳序列。

图3 2 阶差分图Fig.3 2nd order difference diagram

2.1.3 模型定阶 根据图4 可以看出，该时间序列的自相关函数(ACF)值在1 阶后均没有超过置信区间（蓝色区域）；偏自相关函数(PACF)值在2 阶后迅速衰减至接近0，可以考虑p=0 或1、q=0、1 或2。

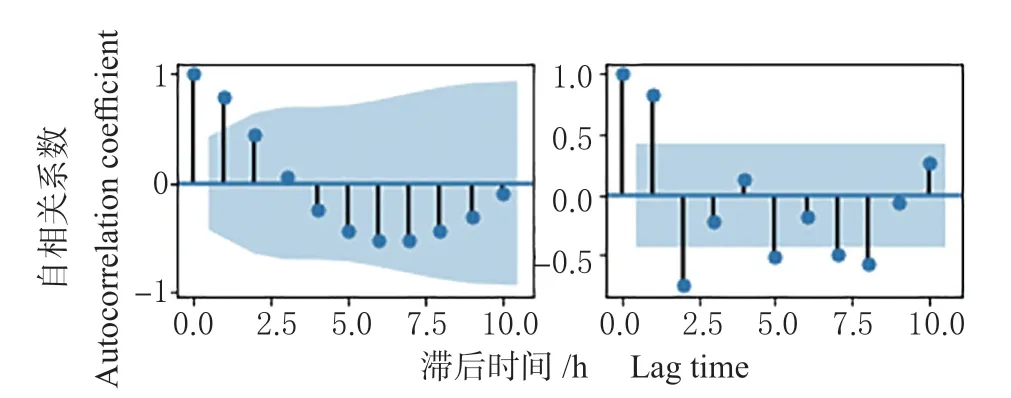
图4 差分后粮食产量数列的ACF 及PACF 图Fig. 4 ACF and PACF of the grain output sequence after difference

2.1.4 模型参数优化 建立ARIMA 模型后，参数根据0、1、2 从低阶到高阶逐个选择，需运用AIC信息准则进行比较择优，当AIC值最小时模型最优。由表1 可以看出，ARIMA(1,2,1)的AIC值小于其余模型，因此ARIMA(1,2,1)为选出的最优模型。

表1 最优模型的选取Table 1 Selection of optimal model

2.1.5 模型验证 将ARIMA(1,2,1)进行白噪声检验后，模型的p值=0.828＞0.05（表2）。

表2 参数检验Table 2 Parameter test

证明ARIMA(1,2,1)模型对该时间序列拟合效果良好。

2.1.6 模型预测 运用上述得到的ARIMA(1,2,1)模型对保定市1996—2014 年粮食产量进行拟合，2015—2017 年粮食产量进行预测，模型的预测结果和相对误差如表3 所示。

表3 保定市粮食产量预测值Table 3 Predicted value of grain output in Baoding City

2.2 粮食产量预测ARIMA-GRNN 组合模型的建立

运用上述ARIMA 模型预测粮食产量各影响因素的变化趋势并结合GRNN 多元回归模型对粮食产量进行预测。

2.2.1 ARIMA-GRNN 模型输入的确定 从《保定市经济统计年鉴》中选取16 个候选输入变量，包括保定市受灾面积、农业机械总动力、农林牧渔业总产值、当年实际机耕地面积、当年机械播种面积、粮食播种面积、粮食播种单产、小麦播种面积、小麦播种单产、小麦总产量、玉米播种面积、玉米播种单产、玉米总产量、农用化肥施用量、农药使用量、有效灌溉面积。因此当年机械播种面积、小麦总产量、玉米播种面积、农用化肥施用量、玉米总产量（图5）为使用皮尔逊相关性分析（图6）筛选出的粮食产量预测的5 个“最佳”输入变量作为GRNN 神经网络的输入。

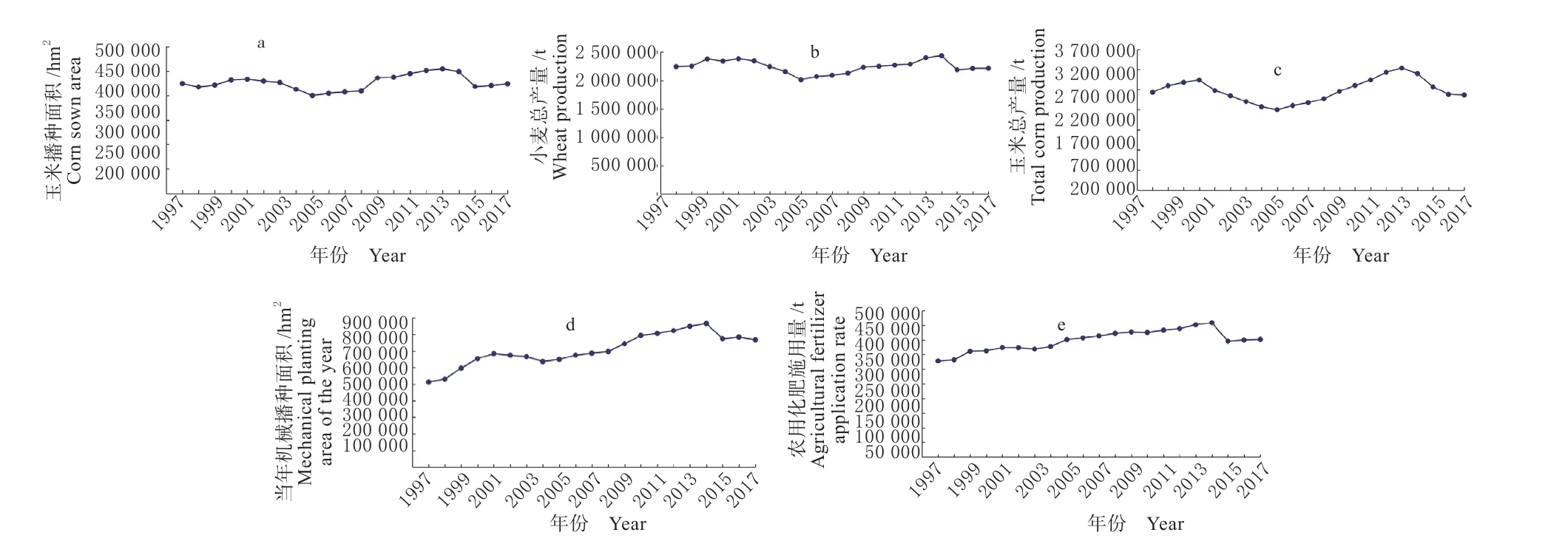
图5 影响因子Fig. 5 Influence factor

图6 变量皮尔逊相关系数矩阵Fig. 6 Variable Pearson correlation coefficient matrix

2.2.2 ARIMA-GRNN 建模 本研究将1996—2014年粮食产量5 个影响因子作为输入样本，将2015—2017 年粮食产量预测值作为输出样本。选择2015—2017 年保定市粮食产量预测值和实际值作为测试样本。通过对GRNN 模型进行训练，确定的最优光滑因子spread=0.02。

2.3 预测模型分析

为了与ARIMA 模型、ARIMA-GRNN 组合模型进行性能比较，将LSTM 模型也应用于相同的训练和测试数据，结果列于表4。结果表明，GRNN 模型预测2015、2016、2017 年保定市粮食产量分别为503.8、505.6、503.7 万t，ARIMA-GRNN 组合模型预测的的平均相对误差为0.47%；ARIMA 模型预测的平均相对误差为0.96%；LSTM 模型预测的平均相对误差为2.20%。相比之下，ARIMA-GRNN 组合模型在预测方面表现优异。

表4 模型拟合及预测误差Table 4 Model fitting and prediction error

3 结论与讨论

本研究使用1 组粮食产量影响因素和3 个机器学习模型分析了数据驱动的粮食作物产量预测方法的性能。预测结果表明，ARIMA-GRNN 组合模型可以作为粮食作物产量预测的有利方法。本研究通过对已有文献的研究发现，在众多学者对粮食产量的预测中，陈鼎玉等人利用ARIMA 模型预测粮食产量，将预测误差控制在4.06%左右［19］。郭亚菲,樊超, 闫洪涛通过主成分分析和粒子群优化神经网络组合模型，预测我国粮食产量的平均相对误差在2%左右［20］。本研究利用Python 对保定市粮食产量预测进行研究发现，ARIMA-GRNN 组合模型在准确性和稳定性方面都优于其他算法，而ARIMA模型和LSTM 模型则没有优势，尤其是对于小特征空间的数据集。ARIMA-GRNN 组合模型较好地拟合了粮食产量的动态发展过程，并预测了保定市近3 年粮食产量的发展趋势。不仅为粮食生产研究提供了准确有效的预测方法，还为其他领域的预测研究提供借鉴。

本研究的不足之处在于，仅选取了16 个影响粮食产量的因子，未考虑到气温、降水、日照时间、土壤湿度等因素对粮食产量的影响，以更准确、全面地反映多种因素对粮食产量的影响。这种方法有助于多尺度全方面地对粮食产量进行准确的预测，可进一步从数据中挖掘经济效益。

在未来的工作中，本课题组将扩展各种数据集，更新气候预测模型和生长阶段模型，并进一步检验所提出模型的有效性和准确性。