一种基于事件触发的分布式卡尔曼一致性滤波算法设计

刘春玉， 孙书利

(黑龙江大学电子工程学院，哈尔滨，150080)

近年来，基于传感器网络的分布式滤波算法由于在自校正，目标监视和跟踪中的广泛应用而倍受关注[1-3]。一方面，应用分布式估计机制，每个传感器只与邻居的传感器之间进行通信，减少通讯过程中的能量耗损；另一方面，传感器可以根据自身的位置自组网络，网络拓扑结构随着传感器节点的变化动态调整，这大大减少了计算量[4]。受信息交换过程中通信带宽和能量消耗的限制，在保证一定的估计性能的同时，优化传感器到估计器的通信速率也变得尤为重要[5]。因此，基于事件触发的分布式卡尔曼滤波算法应运而生.

与传统的时间触发方法不同，事件触发方法在减轻传输压力方面具有巨大优势。在事件触发机制中，仅在超过特定阈值时才触发传输，文献[6～10]已经提出了多种可选择的触发机制。事件触发机制这一概念最早是在文献[11]中提出的,可以分为确定性触发机制和随机触发机制。在确定性触发机制的基础上，文献[7]通过卡方分布设置触发阈值，该卡方分布由当前时刻和最新触发时间的观测值之差建立。当事件触发的决策变量超过给定阈值时，将观测值用于状态估计。文献[12]提出了一种基于事件驱动的新型分布式卡尔曼滤波算法，该事件驱动方案由更新的协方差触发，该协方差通常用于描述真实值与估计值之间的误差。

在传感器网络中，与集中式体系结构相比，分布式体系结构具有更好的鲁棒性和可靠性。每个传感器都充当一个局部的融合中心，从而大大减少了计算负担。文献[13]研究了具有事件触发机制的系统的分布式估计问题。文献[14]提出了基于矩阵加权的分布式卡尔曼滤波算法。为了提高估计性能，提出了一种卡尔曼一致性滤波结构，即在标准卡尔曼滤波器中增加一个共识项[3]，其中增加的共识项由传感器的邻居估计值与自身估计值之差的和组成。结合事件触发机制和卡尔曼一致性滤波结构，文献[15～16]提出了基于事件触发策略的分布式卡尔曼一致性滤波算法。然而，一致性增益被人为设定以保证滤波器稳定。文献[17]虽然设计了最优一致性增益，但是要求满率通信。

基于上述讨论，本文研究了基于传感器网络的事件触发分布式卡尔曼一致性滤波算法。本文采用增量发送传输机制，与其他传输机制相比，该传输触发机制计算简单，易于实现。每个传感器仅在当前观测值与最新触发时刻的观测值之差的平方超过一定阈值时，才将其观测值传输到相应的估值器，同时，估值器将其估计值发送给邻居。基于传感器的观测和邻居节点的估值，在每个估值器处设计基于事件触发分布式卡尔曼一致性算法。这与文献[16]中人为设置一致性增益的方法不同，我们将设计极小化滤波误差方差上界的最优滤波器增益和一致性增益。也不同于文献[17]要求满率通信，我们采用事件触发机制可节省通信负担。本文的主要贡献包括：在每个传感器节点，通过局部最小化滤波误差方差的上界设计了最优卡尔曼滤波增益和一致性增益，提出了事件触发分布式卡尔曼一致性滤波算法。算法避免了传感器节点估值之间估计误差互协方差阵的计算，可减小计算负担。基于李亚普诺夫方法分析了算法在均方意义上的指数有界性。

1 问题描述

考虑多传感器离散时间线性随机系统：

x(t+1)=Ax(t)+Bw(t)

(1)

zi(t)=Hix(t)+vi(t),i=1,2,…,L

(2)

式中：x(t)∈Rn表示系统状态；zi(t)∈Rmi表示传感器i的观测值；L表示传感器的数量；A、B和Hi是适当维数的时不变矩阵。w(t)∈Rr和vi(t)∈Rmi分别是过程噪声和传感器i的观测噪声。

假设1:w(t)和vi(t)是均值为0、方差分别为Q(t) 和Ri(t)的不相关白噪声。

(3)

式中：E表示数学期望；δij是Kronecker函数。

假设2:初值状态x(0)的均值为μ0，方差为P0且与w(t)和vi(t)不相关。

定义G=(V,E)为传感器的网络拓扑结构图，其中V={1,2,…,L}表示网络中节点集合，E⊆V×V为边集合。本文我们考虑无向图。如果节点j与节点i可以通信，那么节点j和节点i的互为邻居节点。定义传感器i的邻居节点集为Ni={j|(j,i)∈E}，则传感器i的邻居节点总数为di=Ni。

在传感器网络中，传感器的能量是有限的。为了节省传感器的通信能量，采用事件触发通信策略来选择有价值的信息进行传输。控制任务是否执行由事先给定的事件触发条件决定，而不是按时间触发。如果在某一时刻满足触发条件，则意味着事件触发。引入一组伯努利分布随机变量γi(t),i=1～L用于描述事件触发的传输策略。定义：

(4)

(5)

对于估值器到估值器的通信信道，我们假设采用时间触发规则，即估值器每次都将其预测估值发送给它的邻居。我们设计如下的一个基于事件触发的分布式一致性滤波器：

(6)

我们的目标是求出局部最优卡尔曼滤波增益和最优共识增益，以最小化滤波器的滤波误差方差的一个上界。

2 分布式滤波设计

定义I(t,i)为估值器i在t时刻接收到的信息，那么，估值器i从初始时刻到t时刻接收的信息可以表示为：

Ii(t)={I(1,i),…,I(t,i)}

(7)

系统状态估值定义如下：

(8)

估值器i在t时刻的估计误差为：

(9)

则相应的误差协方差矩阵可定义如下：

(10)

引理1：对于任意两个适当维度的矩阵X和Y，以下微分公式成立：

(11)

(12)

式中：∂表示微分；tr(·)表示矩阵的迹。

引理2:对于任意2个向量x,y∈Rn，下列不等式成立：

xyT+yxT≤xxT+yyT

(13)

定理1：系统(1)和(2)在假设1和2条件下的分布式递归卡尔曼滤波器和预报器计算为：

(14)

(15)

滤波误差和预报误差的协方差矩阵上界为：

diCi(t))Pi(t|t-1)(I-γi(t)Ki(t)Hi-

(16)

BQ(t-1)BT

(17)

(18)

Ci(t)=di(I-γi(t)Ki(t)Hi)·

(19)

(20)

(21)

证明：由定义(9)可知，滤波误差可以表示为：

(22)

则滤波误差协方差矩阵为：

diCi(t))Pi(t|t-1)(I-γi(t)Ki(t)Hi-

(I-γi(t)Ki(t)Hi-diCi(t))T+

(23)

按照引理2，可以得到:

(24)

(I-γi(t)Ki(t)Hi-diCi(t))·

diCi(t))T≤di(I-γi(t)Ki(t)Hi-

diCi(t))Pi(t|t-1)(I-γi(t)Ki(t)Hi-

(25)

由此，可将(23)转化为：

Pi(t|t)≤(1+di)(I-γi(t)Ki(t)Hi-diCi(t))·

Pi(t|t-1)(I-γi(t)Ki(t)Hi-diCi(t))T+

(26)

-(1+di)(I-Ki(t)Hi-diCi(t))Pi(t|t-1)·

(27)

-di(I-γi(t)Ki(t)Hi-diCi(t))Pi(t|t-1)+

(28)

当γi(t)=0时，一致性增益为：

(29)

其中，Mi(t)由式(20)定义。

当γi(t)=1时，滤波增益和一致性增益分别为：

Ci(t)=di(I-γi(t)Ki(t)Hi)·

(30)

(31)

由式(6)～(8)，能得到式(14)～(15)，由式(29)～(31)和定义(21)，可以得到式(18)～(19)。由式(1)和定义(8)可以得到预报误差方程：

Aei(t-1)+Bw(t-1)

(32)

基于式(10)和式(32)，可得到式(17)。证毕。

3 有界性分析

为了证明所提出的事件触发的分布式卡尔曼一致性滤波的稳定性，我们给出如下假设。

(33)

此外，以下条件成立:

(34)

(35)

以及

E[Vt+1(ηt+1)|ηt]≤(1-ρ)Vt(ηt)+μ

(36)

则随机过程在均方意义下以概率1指数有界，即:

(37)

定理2:在假设3下，当初始误差有界时，所提出的事件触发的分布式卡尔曼一致性滤波在均方意义下以概率为1有界的。

证明：定义e(t)=[(e1(t))T,…,(eL(t))T]T，其中ei(t)由式(9)定义.定义李亚普诺夫函数：

(38)

γi(t+1)Ki(t+1)vi(t+1)+Ci(t+1)·

Ki(t+1)vi(t+1)+(I-γi(t+1)·

(39)

对于任意的具有相同维数的向量x和y，存在tr{xyT}=xTy，则：

E{Vt+1(e(t+1))|e(t)}=

(40)

根据式(33)和式(34)可知，总存在一个正标量0<ρ≤1和u>0，使得式(37)成立，其中:

(41)

(42)

由引理3可知，所设计的事件触发的分布式卡尔曼一致性滤波在均方意义下是以概率1有界的。

4 数值例子

考虑一个简单的带有4个传感器的线性跟踪系统，拓扑结构如图1所示。

图1 带4个传感器的网络拓扑结构

zi(t+1)=Hix(t+1)+vi(t+1),i=1～4

在仿真中，我们取300个数据。定义[0,K]时间段内传感器到估值器之间的通讯速率为：

我们采用根均方误差来评估跟踪性能，根均方位置误差和速度误差分别定义如下：

在仿真中，当传感器与估计器之间的通信阈值设置为1.2，通信速率为0.675时，传感器1的位置和速度跟踪图像展示在图2中，由图可见具有良好的滤波跟踪性能。4个传感器对目标估计的位置和速度的均方根误差如图3所示。可以看到，在事件触发的通信机制下，所有估值器的根均方误差都是有界的。

图2 滤波器的跟踪性能

图3 不同估值器的根均方误差的比较

为了体现本文算法的优势，将本文提出的次优算法与文献[16]中的次优算法进行比较。首先选出适当的σi使得文献[16]的根均方误差尽可能小。通过仿真实验，可以发现当σi取值过大时滤波器将失去稳定性。在设置阈值为1.2时，不同传感器的位置和速度的根均方误差随σi的变化情况如表1所示。可见当σ1=σ2=0.01，σ3=σ4=0.1时根均方误差接近最小。本文算法与文献[16]算法的4个传感器平均根均方误差的比较结果如图4所示。由图可知，本文算法的滤波精度高于文献[16]。

表1 不同σi时的根均方误差

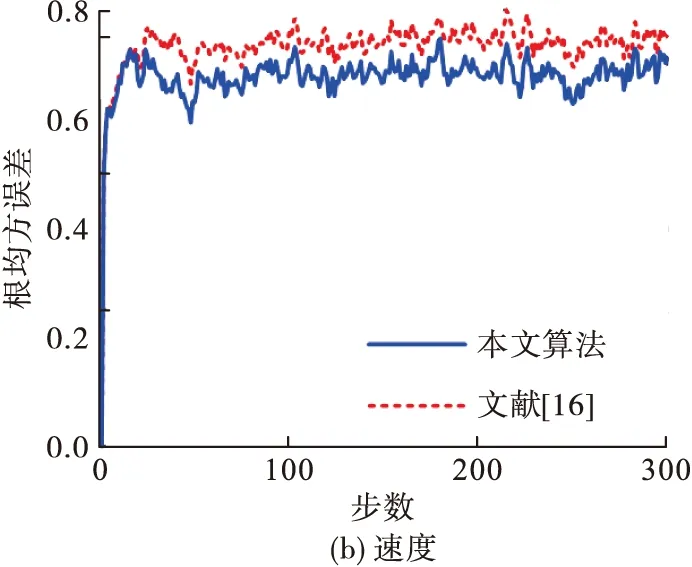
图4 本文算法与文献[16]的根均方误差的比较

4个传感器在不同阈值下的平均根均方误差如图5所示。将传感器与估值器之间通信的阈值分别设置为0、0.6、2、3.6，当阈值为0时为满率通信，平均根均方误差最小。随着阈值的增大，其相应的4个传感器的平均根均方误差也增大。也就是说，阈值越小，通信速率越高，估计精度越高；阈值越大，通信速率越低，估计精度越低。

图5 不同阈值时估值器的根均方误差的比较

当阈值取为1.2时，4个传感器的触发时刻在图6中表示。其中，横坐标表示时刻，纵坐标表示在各时刻各传感器的触发情况，画点处表示此时观测值传输给估值器。为了使得系统在估计性能和通信率之间达到一个平衡，可以适当调节事件触发的阈值，达到既能缓解通信负担又能满足实际估计精度要求的目的。以上仿真验证了算法的有效性。

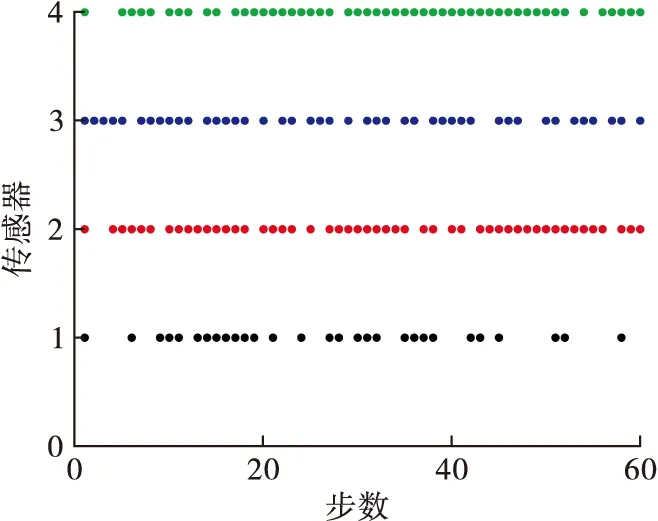
图6 传感器的触发时刻

5 结语

为了避免节点之间估计误差互协方差阵的计算，本文提出了一种基于事件触发的分布式卡尔曼一致性滤波算法。其中，通过局部极小化滤波误差方差的一个上界求解了最优的卡尔曼滤波增益和一致性增益。通过带4个传感器的仿真例子说明了由于避免任两个传感器之间的估计误差互协方差阵每时刻减少的计算量级为O(48)。当传感器的数量较多时，该算法在减小计算量上具有明显的优势。同时，基于李雅普诺夫方法分析了该算法在均方意义上的指数有界性。