氮磷比对湖泊富营养化模型参数敏感性的影响

王玉琳,汪 靓,华祖林,陈 丹,程浩淼,李 嘉,程吉林,刘 芳

氮磷比对湖泊富营养化模型参数敏感性的影响

王玉琳1,汪 靓2*,华祖林3,陈 丹1,程浩淼1,李 嘉1,程吉林2,刘 芳4

(1.扬州大学环境科学与工程学院,江苏 扬州 225127；2.扬州大学水利科学与工程学院,江苏 扬州 225009；3.河海大学环境学院,浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098；4.江苏省水文水资源勘测局扬州分局,江苏 扬州 225002)

运用Morris方法研究了蓝藻暴发期不同氮磷比条件下,巢湖富营养化模型中蓝藻、溶解有机碳、营养物和溶解氧的参数敏感性.结果表明:蓝藻的敏感参数随氮磷比不同有显著差异;氮缺乏情况下,蓝藻对氮转化过程相关参数较敏感;磷缺乏情况下则反之.在任何氮磷比条件下,溶解有机碳、营养物和溶解氧等非生物变量都是对直接参与其自身转化过程的参数最为敏感,它们在不同氮磷比情况下的敏感参数差异较小.相比较蓝藻生长过程的参数,基础代谢过程的参数对所有变量的影响都更强.此外,各个参数的敏感性与它们的相互作用强度呈显著正相关,且这种相关性在极端氮或磷缺乏情况下尤为显著.本研究的结果有助于深入理解湖泊富营养化现象、改善富营养化模型模拟效果和精度.

氮磷比；参数敏感性；巢湖；富营养化模型；Morris方法；EFDC模型

湖泊富营养化问题日益突出已成为全球性的生态环境问题[1].我国长江中下游地区的绝大多数淡水湖泊都已处于富营养化状态[2-4].富营养化模型是研究湖泊富营养化状态,预测其发展过程和趋势的重要工具,而富营养化模型参数估计的准确性对模拟效果有着重要影响[5-8].湖泊富营养化模型通常包含近百个难以直接获取的参数,众多参数的存在使模型参数的准确率定难以实现,因此有必要对模型进行参数敏感性分析[7,9-10],筛选出对模型计算结果有着重要影响的参数以便于进一步研究.此外,参数的敏感性分析对研究和理解湖泊富营养化过程也有着非常重要意义[11-13].

敏感性分析方法分为局部敏感性和全局敏感性方法[14-15].局部敏感性方法依赖于导数概念,因此必然只能考察参数在特定值附近的重要性.相比较局部敏感性方法,全局敏感性方法不仅考虑了参数在整个取值范围内对模型输出结果的整体影响,而且可以考虑参数间的相互作用.目前,常用的全局敏感性分析有回归分析法[15-16]、基于方差分解的方法[17-18]、Morris方法[19-20]等.其中,回归分析方法中当模型所有输入同时影响模型输出时,可评价每个输入因子的敏感性;但当模型为非线性或非单调时,此方法的效果通常不理想.基于方差分解的方法几乎都需要蒙特卡洛采样辅助,因此该类方法需要的计算量非常大,对于具有较多参数的湖泊富营养化模型,个人计算机难以承受参数的敏感性分析. Morris方法是一种理论简单,仅通过较少的模型计算次数便可以获得模型参数的敏感性结果,是识别筛选出对模型重要参数的方法;虽然该方法只能给出参数重要性的排序,但适用于包含较多参数的复杂模型.

参数的敏感性分析是湖泊富营养化模型的研究热点之一.Pastres等[21]对一个三维富营养化模型进行敏感性分析,研究结果表明氮负荷在控制系统初级生产力中起着重要作用. Jiang等[22]研究了大型浅水湖泊太湖水质模型参数的敏感性,结果表明与藻类动力学相关的参数、光照和温度相关的参数对模型输出结果具有较大的影响.王玉琳[23]对二维巢湖富营养化模型参数的敏感性进行分析,研究了模型参数的敏感性随着藻类生消阶段的变化规律及其空间分布特征,发现参数的敏感性随着空间和藻类生消阶段的变化而变化.Ciric等[24]比较了两种敏感性分析方法对水生生态食物网模型参数的敏感性分析的结果,并区分了有影响和无影响的参数. Salacinska等[25]研究了二维GEM模型在藻类爆发期的敏感参数,并进一步利用敏感性分析结果降低模型输出的不确定性.Wang等[11]利用改进的Morris方法分析了巢湖富营养化模型参数对模型结果总体的敏感性.伊璇等[26]对滇池水质模型参数的敏感性进行分析,并获得了参数的样本数量,取值范围与度量方式对参数敏感性的影响.这些文献都集中于模型参数本身的敏感性的研究,而极少研究模型输入和结构对参数敏感性的影响.

水体的氮磷比对富营养化湖泊中藻类生消过程有着十分重要的影响,而富营养化模型是刻画藻类生消过程的重要数学工具;因此,氮磷比必然对富营养化模型参数的敏感性产生显著影响.目前的研究主要聚焦于确定营养物条件下参数敏感性的分析,不同氮磷比对模型参数敏感性的影响研究较少.本文以东部浅水湖泊巢湖为例,运用Morris方法研究了蓝藻爆发期氮磷比对环境流体代码(EFDC)富营养化模型参数敏感性的影响;结果表明,不同氮磷比条件下该模型的参数敏感性有明显的区别.这一研究发现可为快速率定富营养化模型参数,进一步改善和提升模拟效果和精度提供参考.

1 材料与方法

1.1 巢湖富营养化模型

EFDC模型[27]是美国环境保护署资助开发的水环境模型,也是最大日负荷量(Total Maximum Daily Loads,TMDL)计划推荐的主要水环境模型之一. EFDC自带有包含藻类、氨氮、硝酸盐氮、磷酸盐、有机磷、溶解氧、生化需氧量等在内的21种水质变量输移和转化的富营养化模块,其已被广泛应用于湖泊、水库、海湾和河口等多种水体富营养化问题的研究[13,28-32],在我国太湖[22,33]、巢湖[34-35]和滇池[36-37]等水体中也有研究和应用.

本文在EFDC的富营养化模块基础上,根据夏季巢湖的环境特征和研究目标对EFDC模型进行了适当简化.首先,EFDC考虑了湖泊地形和水流运动造成的空间异质性,是基于偏微分方程组(PDEs)的模型,以此为基础研究模型参数的敏感性所需的计算量非常巨大.研究表明[38-40]空间异质性并没有从根本上改变巢湖富营养化模型的平均模拟结果,且参数敏感性的空间差异性不大[23,26,41];因此本研究在不考虑空间异质性的基础上重新实现了EFDC模型的富营养化模块,并将其简化为常微分方程组(ODEs),节省了大量的计算时间.其次,观测表明在夏季巢湖,蓝藻是最主要的藻类[34],因此本研究模型中的藻类仅模拟了蓝藻的生长和消亡过程.经简化后,巢湖富营养化模型包括5个状态变量、63个参数设置、30个过程,模型结构和参数等参见文献[11].

1.2 Morris方法

Morris方法[19-20]是将参数按其取值范围分成若干份,进而研究参数敏感性的方法;但为了处理参数非均匀分布的情况,该方法并非将参数取值范围等分,而是对参数按其概率分布函数等概率抽取,具体如下:

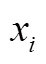
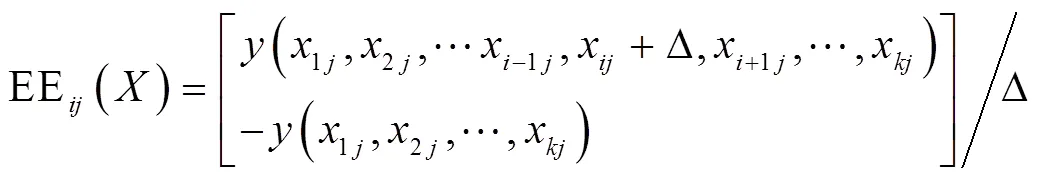
Morris方法选用2个指数µ和来分别衡量参数的敏感性及参数之间的相互作用;且由于该方法抽样的随机性,所以需要进行次重复.

第个输入因子x对模型输出的敏感性:

x与其它参数间的相互作用:

式中:为重复抽样的次数.

1.3 数据来源与处理

数据来源于2009年7～9月巢湖及主要出入河道的监测数据,数据采集点位见图1.其中水质数据的监测约每周1次,出入湖河道流量和来自合肥气象监测站的气象数据(气温、风况、云量等)的监测频率均是1次/d,具体的监测条件参考文献[11].数值计算核心由FORTRAN语言实现,前后处理部分均用R语言[42]来完成,FORTRAN语言的计算核心通过R语言调用,巢湖富营养化模型的求解步长为0.5h.

本研究假设参数服从均匀分布,这对参数的敏感性影响不大;参考文献[11]设置每个参数变化范围为其默认值的±25%,模型评价的次数为=(63+1)´2500=160000,=11.以各变量的平均浓度作为目标;当模型运行总重复次数为2800次时所对应的计算结果类似于2500次的结果,表明后者对于模型参数敏感性分析而言已足够精确;因此,本文参数敏感性分析基于2500次重复抽样的结果;并重点关注藻类、溶解有机碳、磷酸盐、氨氮、硝酸盐氮、溶解氧这6个水环境变量的参数敏感性.

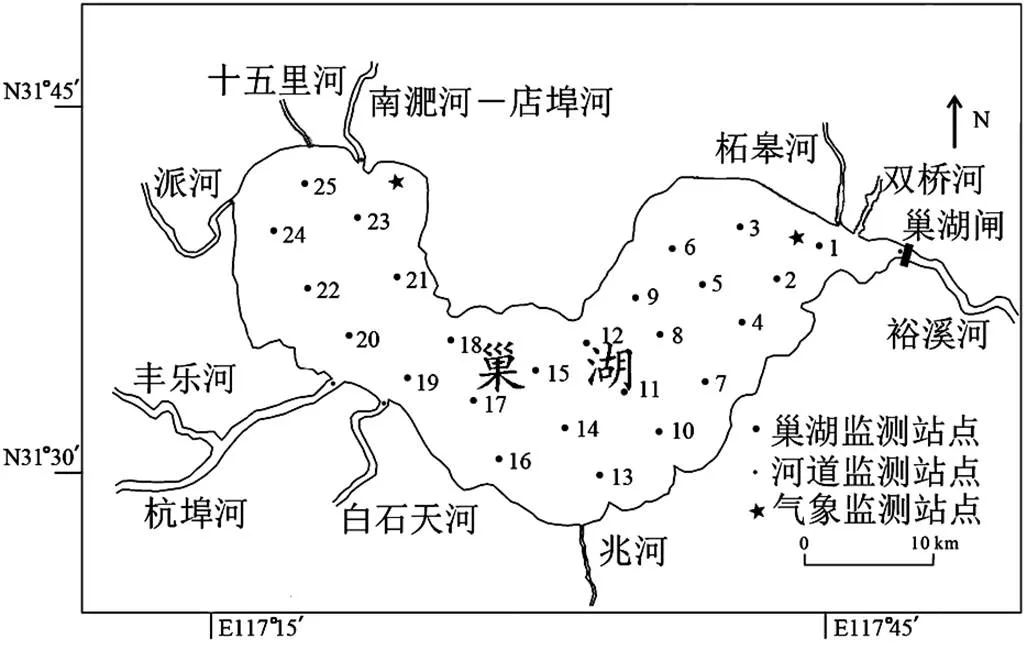
图1 巢湖主要河道及监测站点分布

分析了极端氮限制、氮限制、伪氮限制、磷限制、极端磷限制5种情况下模型参数的敏感性,氮限制和磷限制比的界限设置为16[43].伪氮限制指总氮与总磷的比小于16,但藻类能直接吸收的氨氮和硝酸盐氮总和与磷酸盐的比略大于16的情况,即表观上属于氮限制,实质上属于轻微的磷限制情况.模拟期间,巢湖的监测数据表明其实际处于伪氮限制,因此研究设置的伪氮限制工况即是巢湖氮磷的实际情况;其余4种工况则是在此基础上通过比例缩减或者增加获得.本研究根据蓝藻实际能吸收的氮磷情况将极端氮限制、氮限制归于氮缺乏情况,而伪氮限制、磷限制、极端磷限制归于磷缺乏情况.不同氮磷比限制的设置参见表1.

表1 不同氮磷比限制的设置

2 结果与分析

2.1 蓝藻生物量的参数敏感性分析

图2a中在极端氮限制和氮限制条件下,蓝藻生物量最敏感的参数排列前4的都相同,依次是KDN、BMR、KHN及KTB,而第5个敏感参数分别是KTHDR和KDNALG.其中,KDN、KHN、KTHDR及KDNALG是与溶解有机氮的矿化和颗粒有机氮的水解有关的参数,即与有机氮转化为无机氮的过程有关;这表明在氮缺乏情况下,有机氮转化为无机氮的相关参数是影响蓝藻生物量最为重要的参数.BMR、KTB是分别与蓝藻的基础代谢相关的参数;由于本研究时段巢湖正处于夏季蓝藻暴发时期,蓝藻的生物量已经接近顶峰,此时蓝藻的基础代谢相关参数对藻类生物量的影响较大,其重要性显著大于与蓝藻生长相关的参数.

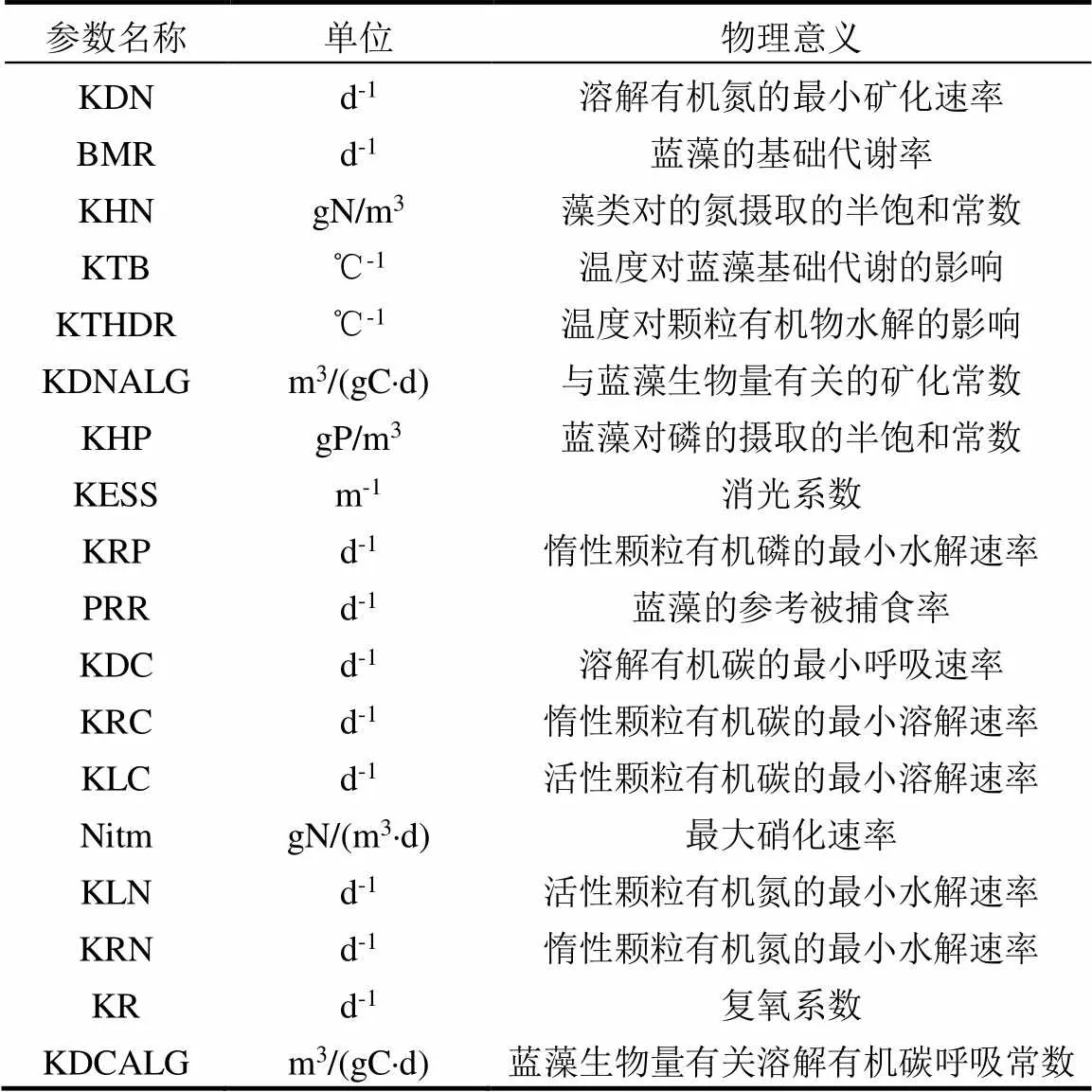
表2 巢湖富营养化模型的敏感参数

相比之下,图2b显示,在磷缺乏的3种情况下,蓝藻生物量的敏感参数的种类和排序是基本一致的,与氮转化相关的参数重要性均大幅下降;而与磷转化相关的参数重要性提高.其中,对于蓝藻生物量最为敏感的参数是KHP,其与有机磷的水解、矿化以及蓝藻生长的营养物限制均有关,这与磷限制的背景相符.在伪氮限制和磷限制2种氮磷比情况下,BMR与KTB仍分别为排名第2和第3敏感参数,这表明蓝藻的基础代谢相关的参数对于蓝藻生物量而言仍是非常重要的;但是与氮缺乏情况不同,消光系数KESS的重要性提高,表明蓝藻生长相关参数的作用重要程度有所上升.极端磷限制下的情况类似于前2种磷缺乏情况,但显然有机磷转化为无机磷过程的相关参数如KRP的重要性进一步提高;这表明在无机磷极端缺乏的环境中,有机磷向无机磷的转化过程对蓝藻生长更为重要.

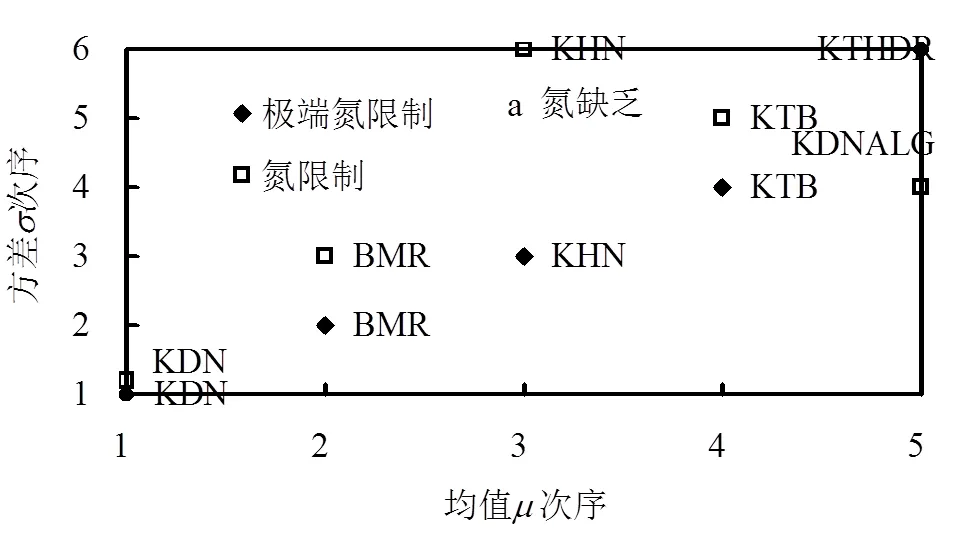
从图2中还可以发现,敏感性较强的参数与其它参数的相互作用均很强,排名前5的敏感参数其相互作用指数的排名均位于前10以内.

2.2 非生物变量的参数敏感性分析

图3a中,在极端氮限制与氮限制,即氮缺乏条件下,溶解有机碳的敏感参数排列前5都相同,依次是KDC、KRC、KDCALG、KTHDR、KLC.其中,KDC和KDCALG均是与溶解有机碳的消耗过程相关的参数;KRC、KLC和KTHDR是分别与颗粒有机碳水解生成溶解有机碳过程相关的参数;即这5个参数都是直接参与溶解有机碳生成过程或是转化过程.

图3b中可以发现,伪氮限制、磷限制和极端磷限制这3种磷缺乏情况下,溶解有机碳的最敏感参数排序完全相同.与氮缺乏情况比较也只是个别参数排序略有差异,如参数KDCALG在磷缺乏情况下的重要性要比在氮缺乏情况下对溶解有机碳更重要.但不论是氮缺乏还是磷缺乏情况下,参数敏感性排名均表明溶解有机碳最敏感的参数都是与其生成和消耗直接相关的参数;相较于如蓝藻生长、死亡和营养物的转化等过程,碳的自身转化过程相关的参数对溶解有机碳的影响更为重要.

比较图4a和4b结果可以发现,在不同的氮磷比条件下,磷酸盐的敏感性参数排列前5都相同,依次是KRP、KHP、KTHDR、BMR、KTB.其中, KRP、KHP、KTHDR分别是与颗粒有机磷的水解、溶解有机磷的矿化过程相关的参数;BMR和KTB均是与蓝藻的新陈代谢过程相关的参数.磷酸盐最敏感参数的结果表明,相比较蓝藻对无机磷的摄取等生长过程,蓝藻的基础代谢过程和有机磷的水解和矿化过程相关的参数对磷酸盐的影响更重要;这应该与研究时期巢湖蓝藻生物量已接近顶峰有关.

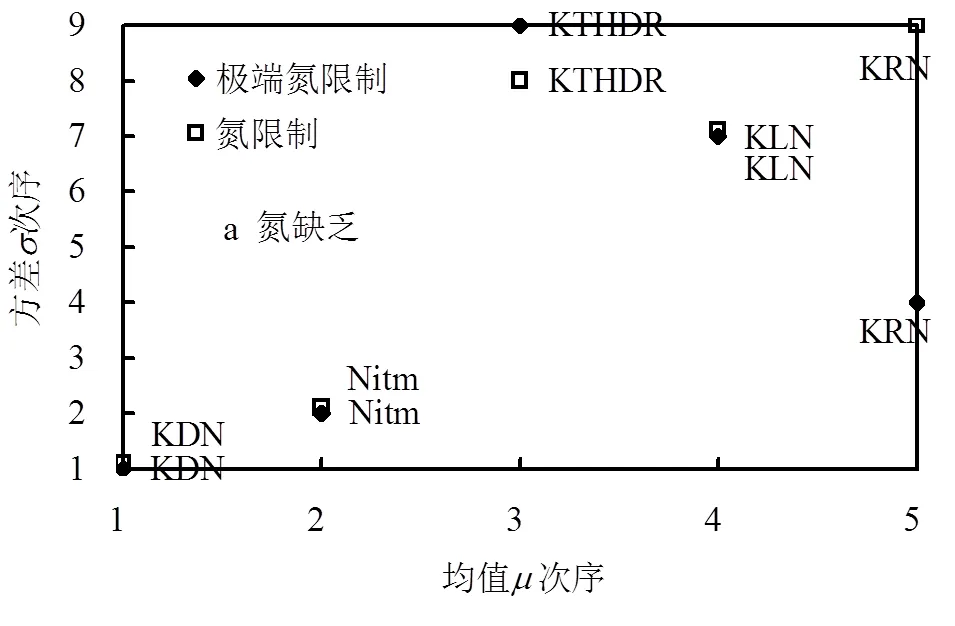
类似于磷酸盐的参数敏感性分析结果,图5a和5b中可以发现,在不同氮磷比条件下,氨氮的敏感参数排列前5也是一致的,依次是KDN、Nitm、KTHDR、KLN、KRN.其中,KDN和Nitm分别是与溶解有机氮矿化和氨氮的硝化过程相关的参数;KTHDR、KLN、KRN均是与颗粒机氮的水解过程有关的参数.以上敏感参数的排名结果表明在任何营养限制下,颗粒有机氮的水解和溶解有机氮的矿化过程等氨氮生成过程和氨氮的硝化过程对氨氮而言最为重要,即氨氮对其自身转化过程直接相关的参数最为敏感,而蓝藻生消过程相关的参数对氨氮的影响则较小.

图6a中,在极端氮限制和氮限制条件下,硝酸盐氮最敏感参数排列前5的参数也是相同,依次是Nitm、KDN、KHN、KTB、BMR.其中,Nitm表示最大的硝化速率,直接影响硝酸盐氮的生成过程的重要参数;KDN和KHN是与有机氮的水解和矿化过程相关的参数;KTB和BMR是与蓝藻的基础代谢过程相关的参数,影响硝酸盐氮的浓度的变化过程.这说明氮缺乏情况时,硝酸盐氮生成过程的相关参数更敏感;也说明当蓝藻数量到接近顶峰后,蓝藻的消亡比其生长吸收氮等营养元素的过程对硝酸盐氮有着更重要的影响.

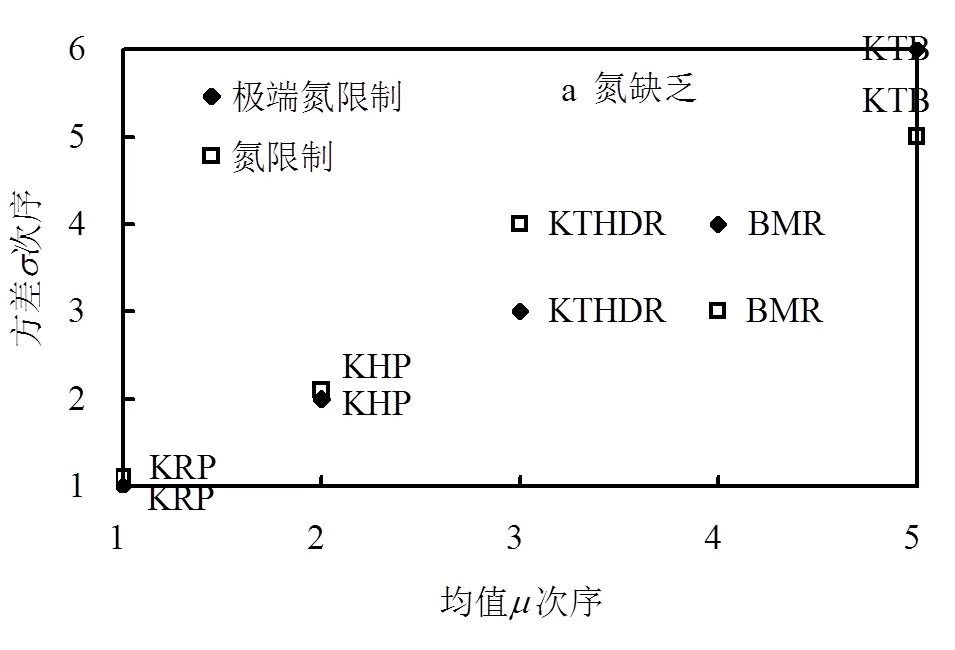
图6b中,在磷缺乏情况下,随着磷限制的增强Nitm和KDN仍为最敏感的参数,但与蓝藻的基础代谢过程相关参数(如BMR和KTB)的重要性逐渐减弱,甚至参数KTB的敏感性指数排名在极端磷限制情况下已经超出前10,而与反硝化过程相关参数KDC、KTHDR的重要性逐渐增强.这表明在磷缺乏情况下,硝酸盐氮转化涉及的硝化过程和反硝化过程是最重要的,而蓝藻的基础代谢过程则对硝酸盐氮的影响相对较小.

总之,对于营养物而言与其各自转化过程直接相关的参数是其最为敏感的参数.在蓝藻暴发期,由于蓝藻数量已经接近顶峰,蓝藻基础代谢作用的参数对营养物更为重要.

图7a中,极端氮限制和氮限制条件下,溶解氧的参数敏感性排名前5一致,依次是KDC、KR、KRC、KTHDR、KDCALG.其中,KDC、KRC、KTHDR、KDCALG均是与溶解有机碳的生成和矿化过程相关的参数,而这些过程都直接影响着水中溶解氧的浓度大小;KR表示复氧系数,它是关于溶解氧浓度增加速度的重要参数.这表明在氮缺乏情况下,溶解氧的消耗和复氧过程直接相关的参数对水中溶解氧浓度较为重要.从图中还可以再次发现,敏感性指数排名靠前的参数其与其它参数的相互作用强度排名也靠前.

图7b中,在磷缺乏情况下,KDC、KDCALG以及KR的敏感性指数仍排名前5,它们是对溶解氧非常重要的参数;但随着磷限制的增强,参数KHP的敏感性显著增加;从氮缺乏情况中KHP排名未进入前5,而在磷缺乏情况下列入第2,分析原因可能是磷元素影响蓝藻的生长等过程,因此KHP可以间接影响溶解氧.

2.3 讨论

蓝藻生物量是由生长、基础代谢和被捕食等过程共同决定,其中生长过程受到营养物浓度、光照和温度等条件限制[27].本研究期间处于巢湖夏季,其温度和光照等条件几乎都处于最适宜蓝藻生长的情况[44-45],因此营养物的情况可能成为限制蓝藻生长的主要因子.进一步,大多数富营养化模型,包括本研究的巢湖富营养化模型对藻类生长速率的描述公式都表达为最大增长率与限制因子的乘积[38],其中营养物相关的限制因子一般由磷和氮中相对缺乏的营养物浓度及相关参数构成;氮缺乏时,磷转化过程参数不参与藻类生长过程的计算,这是氮缺乏情况下蓝藻对氮转化过程相关参数较敏感的原因,反之亦然.一般地,营养物对藻类生长的限制作用,取决于水体是氮缺乏还是磷缺乏;当其中一种营养物相对丰富时,另一种营养物就对藻类生长起到决定作用,从而对该种营养物转化过程有直接作用的参数自然也就成为藻类生物量的敏感参数.这也是藻类生物量的敏感参数随氮磷比变化有所不同的原因.本研究结果也证实了蓝藻的敏感参数受不同氮磷比情况的影响这一结论.

除与氮磷转化过程相关的参数外,任何氮磷比情况下,蓝藻生物量都对直接控制藻类生消动力学的参数,如BMR、KTB等敏感,这与已有文献的结论相一致[11,22].

溶解有机碳、营养物和溶解氧等非生物变量的参数敏感性对氮磷比条件依赖较弱.无论氮磷比如何变化,对非生物变量而言,最敏感的参数都是对其自身转化有直接影响的参数.如对于氨氮和硝酸盐氮而言,不论是哪种氮磷比情况,Nitm和KDN均是其较为敏感的参数,这一结果与已有文献中的结论类似[10,23].这是因为,非生物变量的转化过程中不存在类似于藻类生长过程中随着氮磷比的改变从氮限制转变为磷限制的机制,即氮磷比难以从根本上改变非生物变量的转化过程的特征.氮磷比主要通过对藻类的生长和新陈代谢过程的影响才能对非生物变量参数敏感性产生间接影响;而不能直接影响这些参数在非生物变量转化过程中的作用[27];因此,非生物变量的参数敏感性对氮磷比依赖较弱.

Morris方法不仅可以计算得出参数敏感性指数的排名,还可以计算得到参数与其它参数间的相互作用强度.本文使用秩相关系数计算了不同氮磷比条件下,巢湖富营养化模型的63个参数的敏感性和相互作用强度的相关系数,结果见表3.

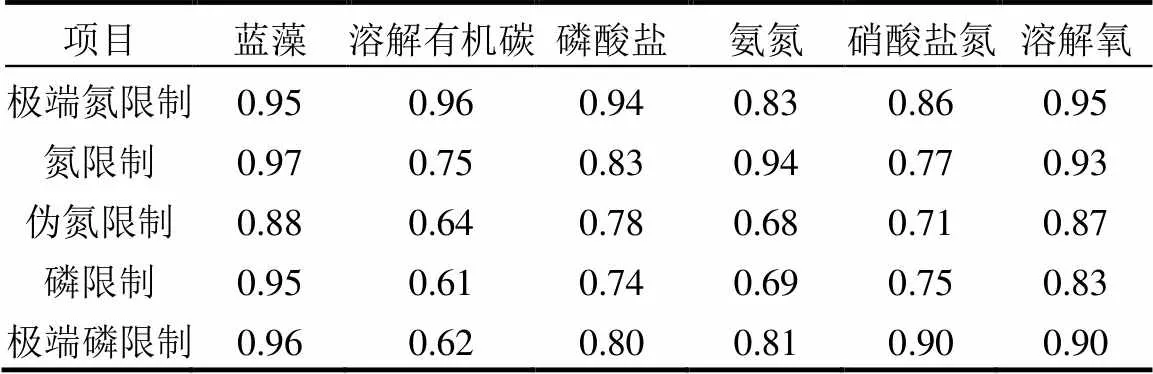
表3 参数敏感性和相互作用强度的相关系数

注:显著性<0.01.

表3中可以发现敏感性较强的参数与其它参数间的相互作用也较强,两者的相关系数均大于0.60,为显著正相关.进一步分析发现不同变量的情况有所区别:对于蓝藻、营养物和溶解氧,在氮或磷缺乏较明显时它们的参数敏感性和相互作用强度的正相关程度均较高,如极端氮限制情况下,对应的相关系数均大于0.80;而氮磷比处于中间时,对应的相关系数则相对较小;溶解有机碳参数的敏感性和相互作用强度的相关系数则随着氮磷比的增大而呈现出逐渐减小的趋势.

3 结论

3.1 不同氮磷比条件下,蓝藻生物量的敏感参数显著不同,受到营养物限制的影响;而溶解有机碳、营养物、溶解氧等非生物变量的参数敏感性对氮磷比的依赖相对较弱.

3.2 溶解有机碳、营养物和溶解氧等都对其自身转化过程直接相关的参数最为敏感.在蓝藻爆发期,蓝藻数量已接近顶峰,所以非生物变量对蓝藻基础代谢过程相关的参数比蓝藻生长过程相关参数更为敏感.

3.3 敏感性较强的参数与其它参数的相互作用也较强,二者呈显著的正相关关系.在氮或磷缺乏较明显的情况下,蓝藻、营养物和溶解氧的参数敏感性和相互作用强度的正相关程度均较高.

[1] 金相灿.湖泊富营养化控制和管理技术 [M]. 北京:化学工业出版社, 2001:2-7.

Jin X C. Lake eutrophication control and management technology [M]. Beijing: Chemical Industry Press, 2001:2-7.

[2] 秦伯强,高 光,朱广伟,等.湖泊富营养化及其生态系统响应 [J]. 科学通报, 2013,58(10):855-864.

Qin B Q, Gao G, Zhu G W, et al. Lake eutrophication and its ecosystem response [J]. Chinese Science Bulletin, 2013,58(10): 855-864.

[3] 成小英,李世杰.长江中下游典型湖泊富营养化演变过程及其特征分析 [J]. 科学通报, 2006,51(7):848-855.

Cheng X Y, Li S J. Eutrophication evolution process and its characteristics of typical lakes in the middle and lower reaches of the Yangtze River. [J]. Chinese Science Bulletin, 2006,51(7):848-855.

[4] 陈小锋,揣小明,杨柳燕.中国典型湖区湖泊富营养化现状、历史演变趋势及成因分析 [J]. 生态与农村环境学报, 2014,30(4):438-443.

Chen X F, Chuai X M, Yang L Y. Status quo, historical evolution and causes of eutrophication in lakes in typical lake regions of China [J]. Journal of Ecology and Rural Environment, 2014,30(4):438-443.

[5] Ji Z G. Hydrodynamics and water quality: modeling rivers, lakes, and estuaries [M]. New York: Wiley, 2017:161-376.

[6] Chen X J. Dynamic coupling of a three-dimensional hydrodynamic model with a laterally averaged, two-dimensional hydrodynamic model [J]. Journal of Geophysical Research Atmospheres, 2007,112(C7):623-642.

[7] Wang Y L, Cheng H M, Wang L, et al. A combination method for multicriteria uncertainty analysis and parameter estimation: a case study of Chaohu Lake in Eastern China [J]. Environmental Science and Pollution Research, 2020,27:20934-20949.

[8] Wang Y L, Hua Z L, Wang L. Parameter estimation of water quality models using an improved multi-objective particle swarm optimization [J]. Water, 2018,10(1):32.

[9] Sarrazin F, Pianosi F, Wagener T. Global sensitivity analysis of environmental models: convergence and validation [J]. Environmental Modelling & Software, 2016,79:135-152.

[10] Yi X, Zou R, Guo H C. Global sensitivity analysis of a three- dimensional nutrients-algae dynamic model for a large shallow lake [J]. Ecological Modelling, 2016,327:74-84.

[11] Wang Y L, Hua Z L, Wang L. Sensitivity analysis of the Chaohu Lake eutrophication model with new index based on Morris method [J]. Water Science and Technology: Water Supply, 2018,18(4):1375-1387.

[12] Zheng W, Shi H H, Fang G H, et al. Global sensitivity analysis of a marine ecosystem dynamic model of the Sanggou Bay [J]. Ecological Modelling, 2012,247(4):83-94.

[13] Li Y P, Tang C Y, Zhu J T, et al. Parametric uncertainty and sensitivity analysis of hydrodynamic processes for a large shallow freshwater lake [J]. Hydrological Sciences Journal, 2015,60(6):1078-1095.

[14] Cariboni J, Gatelli D, Liska R, et al. The role of sensitivity analysis in ecological modelling [J]. Ecological Modelling, 2007,203(1/2): 167-182.

[15] Pianosi F, Beven K, Freer J, et al. Sensitivity analysis of environmental models: A systematic review with practical workflow [J]. Environmental Modelling & Software, 2016,79:214-232.

[16] 宋晓猛,张建云,占车生,等.水文模型参数敏感性分析方法评述 [J]. 水利水电科技进展, 2015,35(6):105-112.

Song X M, Zhang J Y, Zhan C S, et al. Review of methods of parameter sensitivity analysis in hydrologic modeling [J]. Advances in Science and Technology of Water Resources, 2015,35(6):105-112.

[17] Saltelli A, Tarantola S, Chan P S. A quantitative model-independent method for global sensitivity analysis of model output [J]. Technometrics, 1999,41(1):39-56.

[18] Sobol I M. Sensitivity estimates for nonlinear mathematical models [J]. Mathematical Modeling & Computational Experiment, 1993,1(4): 407-414.

[19] Morris M D. Factorial sampling plans for preliminary computational experiments [J]. Technometrics, 1991,33(2):161-174.

[20] Campolongo F, Cariboni J, Saltelli A. An effective screening design for sensitivity analysis of large models [J]. Environmental Modelling & Software, 2007,22(10):1509-1518.

[21] Pastres R, chan K, Dejak C. Global sensitivity analysis of a shallow- water 3D eutrophication model [J]. Computer Physics Communication, 1999,117:62-74.

[22] Jiang L, Li Y, Zhao X, et al. Parameter uncertainty and sensitivity analysis of water quality model in Lake Taihu, China [J]. Ecological Modelling, 2018,375:1-12.

[23] 王玉琳.巢湖EFDC富营养化模型参数敏感性及优化确定研究 [D]. 南京:河海大学, 2018.

Wang Y L. Research on parameters sensitivity and optimization determination of Chaohu Lake EFDC eutrophication model [D]. Nanjing: Hohai University, 2018.

[24] Ciric C, Ciffroy P, Charles S. Use of sensitivity analysis to identify influential and non-influential parameters within an aquatic ecosystem model [J]. Ecological Modelling, 2012,246:119-130.

[25] Salacinska K, El Serafy G Y, Los F J, et al. Sensitivity analysis of the two dimensional application of the Generic Ecological Model (GEM) to algal bloom prediction in the North Sea [J]. Ecological Modelling, 2010,221(2):178-190.

[26] 伊 璇,郭怀成.三维水动力水质模型不确定性研究 [M]. 北京:科学出版社, 2017:110-125.

Yi X, Guo H C. Research of uncertainty in three-dimensional hydrodynamics and water quality moedel [M]. Beijing: Science Press, 2017:110-125.

[27] Tetra Tech Inc. The environmental fluid dynamics Code Theory and computation, Volum 3: water quality module [R]. Fairfax, VA: Dynamic Solutions International, 2007.说明:这是公司的报告,没有具体作者

[28] Wang P, Lai G Y, Li L. Predicting the hydrological impacts of the Poyang Lake project using an EFDC model [J]. Journal of Hydrologic Engineering, 2015,20(12):05015009.

[29] Qi H D, Lu J Z, Chen X L, et al. Water age prediction and its potential impacts on water quality using a hydrodynamic model for Poyang Lake, China [J]. Environmental Science and Pollution Research, 2016,23(13):13327-13341.

[30] Gong R, Xu L G, Wang D G, et al. Water quality modeling for a typical urban lake based on the EFDC model [J]. Environmental Modeling & Assessment, 2016,21(5):643-655.

[31] Arifin R R, James S C, Pitts DAD, et al. Simulating the thermal behavior in Lake Ontario using EFDC [J]. Journal of Great Lakes Research, 2016,42(3):511-523.

[32] Zhou J T, Falconer R A, Lin B L. Refinements to the EFDC model for predicting the hydro-environmental impacts of a barrage across the Severn Estuary [J]. Renewable Energy, 2014,62:490-505.

[33] 李一平,唐春燕,余钟波,等.大型浅水湖泊水动力模型不确定性和敏感性分析 [J]. 水科学进展, 2012,23(2):271-277.

Li Y P, Tang C Y, Yu Z B, et al. Uncertainty and sensitivity analysis of large shallow lake hydrodynamic models [J]. Advances In Water Science, 2012,23(2):271-277.

[34] Huang J C, Zhang Y J, Huang Q, et al. When and where to reduce nutrient for controlling harmful algal blooms in large eutrophic lake Chaohu, China? [J]. Ecological Indicators, 2018,89:808-817.

[35] 华祖林,刘晓东,褚克坚,等.基于边界拟合下的水流与污染物质输运数值模拟 [M]. 北京:科学出版社, 2013:185-200.

Hua Z L, Liu X D, Chu K J, et al. Numerical simulation of water flow and pollutant transport based on boundary fitting [M]. Beijing: Science Press, 2013:185–200.

[36] 陈异晖.基于EFDC模型的滇池水质模拟 [J]. 云南环境科学, 2005,24(4):28-30.

Chen Y H. Water quality smiulation of Dianchi Lake based on EFDC model [J]. Yunnan Environmental Science, 2005,24(4):28-30.

[37] 杨澄宇,代 超,伊 璇,等.基于正交设计及EFDC模型的湖泊流域总量控制——以滇池流域为例 [J]. 中国环境科学, 2016,36(12): 3696-3702.

Yang C Y, Dai C, Yi X, et al. Total emission control of water pollutant for the lake basin based on orthogonal experimental design and EFDC model: A case study of Dianchi Basin [J]. China Environmental Science, 2016,36(12):3696-3702.

[38] Jorgensen S E. Fundamentals of ecological modelling: applications in environmental management and research [M]. New York: Elsevier, 2011:175-225.

[39] Schwarzenbach R P, Gschwend P M, Imboden D M. Environmental origanic chemistry [M]. New York, USA: Wiley, 2002:945-1004.

[40] Xu F L, Jørgensen S E, Tao S, et al. Modeling the effects of ecological engineering on ecosystem health of a shallow eutrophic Chinese lake (Lake Chao) [J]. Ecological Modelling, 1999,117(2/3):239-260.

[41] 张质明,王晓燕,李明涛.基于全局敏感性分析方法的WASP模型不确定性分析 [J]. 中国环境科学, 2014,34(5):1336-1346.

Zhang Z M, Wang X Y, Li M T. Uncertainty analysis of WASP based on global sensitivity analysis method [J]. China Environmental Science, 2014,34(5):1336-1346.

[42] R Core Team. A language and environment for statistical computing [R]. Vienna, Auatria, 2017.

[43] 李小平.湖泊学 [M]. 北京:科学出版社, 2013:132-135.

Li X P. Limnology [M]. Beijing: Science Press, 2013:132-135.

[44] Kalff J.湖沼学 [M]. 北京:高等教育出版社, 2011:202-208.

Kalff J. Limnology [M]. Beijing: Higher Education Press, 2011:202- 208.

[45] 赵 焕,朱 利,吴传庆,等.基于天地协同的巢湖水华分布特征 [J]. 中国环境科学, 2018,38(6):2297-2303.

Zhao H, Zhu L, Wu C Q, et al. Distribution characteristics analysis of algal bloom in Chaohu Lake based on the sky～earth collaborative method [J]. China Environmental Science, 2018,38(6):2297-2303.

Effect of nitrogen to phosphorus ratio on parameter sensitivity of lake eutrophication model.

WANG Yu-lin1, WANG Liang2*, HUA Zu-lin3, CHEN Dan1, CHENG Hao-miao1, LI Jia1, CHENG Ji-lin2, LIU Fang4

(1.School of Environmental Science and Engineering, Yangzhou University, Yangzhou 225127, China；2.College of Hydraulic Science and Engineering, Yangzhou University, Yangzhou 225009, China；3.Key Laboratory of Integrated Regulation and Resource Development on Shallow Lake of Ministry of Education, College of Environment, Hohai University, Nanjing 210098, China；4.Hydrology and Water Resources Investigation Bureau of Jiangsu Province Yangzhou Bureau, Yangzhou 225002, China)., 2021,41(6)：2893～2901

The Morris method was used to study the sensitivity parameter of cyanobacteria, dissolved organic carbon, nutrients and dissolved oxygen in Chaohu Lake eutrophication model under different nitrogen to phosphorus ratios during the cyanobacteria blooms. As results shown, sensitivity parameters of cyanobacteria were significance different with the ratio of nitrogen to phosphorus. In the case of nitrogen deficiency, cyanobacteria were more sensitive to the parameters of the nitrogen conversion process, and the converse was true in the case of phosphorus deficiency. Under different ratios of nitrogen to phosphorus, non-biological variables such as dissolved organic carbon, nutrients, and dissolved oxygen were more sensitive to the parameters directly related to their own transformation process. Parameters related to the metabolism of cyanobacteria had a greater influence on all variables than that of the growth process. In addition, there was a significant positive correlation between the sensitivity of the parameters that were tested and the strength of the interaction. This was especially true in the case of extreme nitrogen or phosphorus deficiency. These results would be helpful for understanding lake eutrophication and improve the simulation effect and accuracy of eutrophication models.

ratio of nitrogen to phosphorus；sensitive of parameters；Chaohu Lake；eutrophication model；Morris method；EFDC model

X143

A

1000-6923(2021)06-2893-09

2020-10-22

国家自然科学基金资助项目(51909230,51809226,51739002);中国博士后科学基金资助项目(2019M661948);工业生态与环境工程教育部重点实验室开放基金(KLIEEE-17-02);扬州大学科技创新培育基金(2019CXJ094);江苏省资助招收博士后项目(2018Z051,2019Z319)

* 责任作者, 助理研究员, right628@126.com

王玉琳(1986-),女,山西临汾人,助理研究员,博士,主要从事水环境模拟与污染物输移规律研究.发表论文10余篇.