基于反射系数谱的XLPE电缆水树缺陷定位方法

周 湶， 王鑫源， 欧阳希， 姜 茜

(输配电装备及系统安全与新技术国家重点实验室， 重庆大学， 重庆 400044)

1 引言

交联聚乙烯(Cross-linked Polyethylene，XLPE)绝缘材料凭借其优秀的机械电气性能，已经在输配电线路中得到了广泛应用[1]。然而，当电缆受潮后，绝缘介质会在水分和电场的共同作用下形成含水通道，发生水树老化[2]。水树会随着电缆运行而缓慢增长，当水树长度达到电缆绝缘层厚度的60%以上时电缆绝缘的击穿场强将会显著降低，甚至造成停电事故[3]。因此，在电缆水树缺陷尚未发展成为绝缘故障前，对其进行绝缘诊断，及时维修或替换电缆缺陷部分，能够有效预防击穿事故的发生，从而为电网的安全稳定运行提供保障。

为实现对水树缺陷的有效诊断，国内外学者提出了一些新型诊断方法如超低频介损法[4]、空间电荷法[5]、残余电荷法[6]、极化去极化电流法[7]等。虽然上述方法能够有效地诊断出水树老化程度，但仍然缺乏能够对诊断出的水树缺陷进行精确定位的有效方法。

在电缆缺陷定位方面，局部放电法[8，9]可以定位缺陷位置，然而在正常情况下水树缺陷并不会产生局部放电[10]。时域反射法(Time Domain Reflectometry, TDR)[11]通过向待测电缆注入一个脉冲信号，利用反射信号到达监测端的时间差进行定位，然而由于反射信号的传播衰减以及对到达时间测定存在主观性等原因，时域反射法的定位结果可能产生较大误差[12]。频域反射法(Frequency Domain Reflectometry, FDR)利用电缆频率相关量进行缺陷定位[13]。日本Yoshimichi Ohki院士课题组利用傅里叶反变换(Inverse Fast Fourier Transform, IFFT)分析电缆宽频阻抗谱成功定位电缆辐射老化缺陷[14]，并通过试验证明了在定位效果上FDR优于TDR[15]，然而IFFT方法需要测试频率尽可能高(1.5 GHz)，对设备和成本提出了较高的要求。国内学者提出基于反射系数谱的电缆机械损伤缺陷定位方法[16]，通过离散傅里叶变换(Discrete Fourier Transform, DFT)和加窗操作，实现机械损伤缺陷的定位。

事实上，由于水树与热老化、机械损伤缺陷在形成机理、发展周期、外在特征及电气特性等方面均有较大差别，使得FDR对于不同类型缺陷的诊断效果以及诊断灵敏度存在差异。加上目前缺乏对于电缆水树缺陷情况与分布参数之间的影响关系的研究，共同导致国内外尚未开展基于FDR的水树诊断相关研究。此外，目前能用于评估局部水树老化状态的特征量较少，而FDR的宽频特性能够提供表征水树老化情况的新特征量，因此开展基于FDR的水树诊断研究能够有效填补相关研究空缺。

为解决上述问题，本文基于传输线理论构建出水树缺陷下电缆首端反射系数模型，运用有限元仿真方法明确了不同类型水树缺陷对模型中分布参数的关联关系，引入基于广义正交法的缺陷定位模型，提出一种基于电缆首段反射系数谱的水树定位及诊断新方法，并优选出模拟诊断的频带参数。最后通过多组仿真实验及实际电缆实验的分析，验证了本方法的有效性及准确性，为工程实际中电缆的故障预先感知、科学化运维管理提供更有价值的技术支撑。

2 电缆首端反射系数谱

2.1 电缆分布参数模型

由传输线基本原理可知，当电缆线路长度l与入射信号波长λ满足l> 0.1λ时，线路需要看作分布参数网络进行处理[17]。此时电缆等效电路如图1所示，其中单位长度电缆的电阻、电感、电导和电容分别用R0、L0、G0、C0表示。由于趋肤效应和临近效应，单位电阻和电感直接受频率影响，随着频率的增加，单位长度电阻R逐渐增大，电感逐渐减小，则考虑频变效应的单位电阻和电感可以分别由式(1)、式(2)近似[18]：

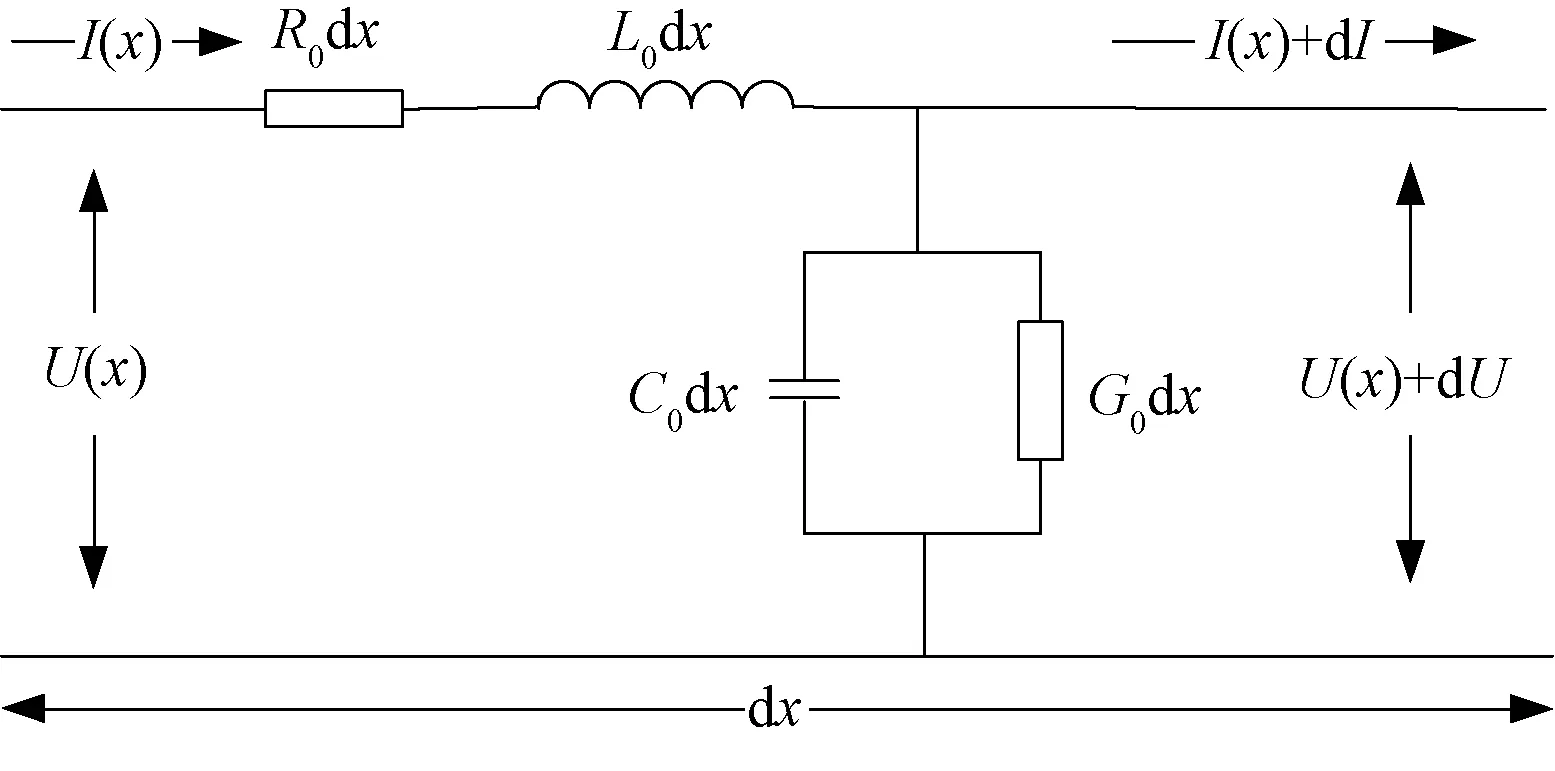
图1 单位长度传输线等效电路Fig.1 Equivalent circuit of transmission line per unit length

(1)

(2)

式中，ω为信号角频率；μ0为真空磁导率；rc为缆芯导体半径；rs为金属屏蔽层内半径；σc和σs分别为缆芯导体和金属屏蔽层的电导率。

单位电容C和电导G频率不直接受频率影响，而与电缆本身特征有关，可以由式(3)计算[18]：

(3)

式中，ε为介质的介电常数；σ为介质电导率。

2.2 含水树缺陷的电缆首端反射系数模型

应用传输线方程对图1电缆分布参数等效电路求解，若电缆总长度为l，可得电缆中距首端x处的电压和电流向量分别为[18]：

(4)

式中，Ui和Ur分别为入射电压波和反射电压波；γ和Z0分别为传播常数和特征阻抗，可以由式(5)、式(6)计算[18]：

(5)

(6)

式中，α和β分别为衰减系数和相位常数。

距离首端x处的反射系数为该处反射电压波与入射电压波之比：

(7)

式中，ZL为负载阻抗。

通常电缆末端负载阻抗可以接触并通过阻抗分析获取。如果电缆负载不可接触，则可以通过基于小波变换的时域反射法[19]测量。当负载端开路时，即ZL= ∞，则x处的反射系数可以表示为：

Γ(x)=e-2γ(l-x)=e-2α(l-x)e-2jβ(l-x)

(8)

在电缆首端(x=0)处，电缆首端反射系数谱为：

Γ(0)=e-2(α+jβ)l=e-2αl[cos(2βl)+jsin(2βl)]

(9)

基于式(5)～式(9)建立含有水树缺陷的反射系数谱模型。如图2所示，一根总长为l的电缆，la至lb为水树缺陷段。将该电缆分为三部分计算，(0,la)、(la,lb)、(lb,l)。其中每一部分以式(7)为基础，计算其首端反射系数为：

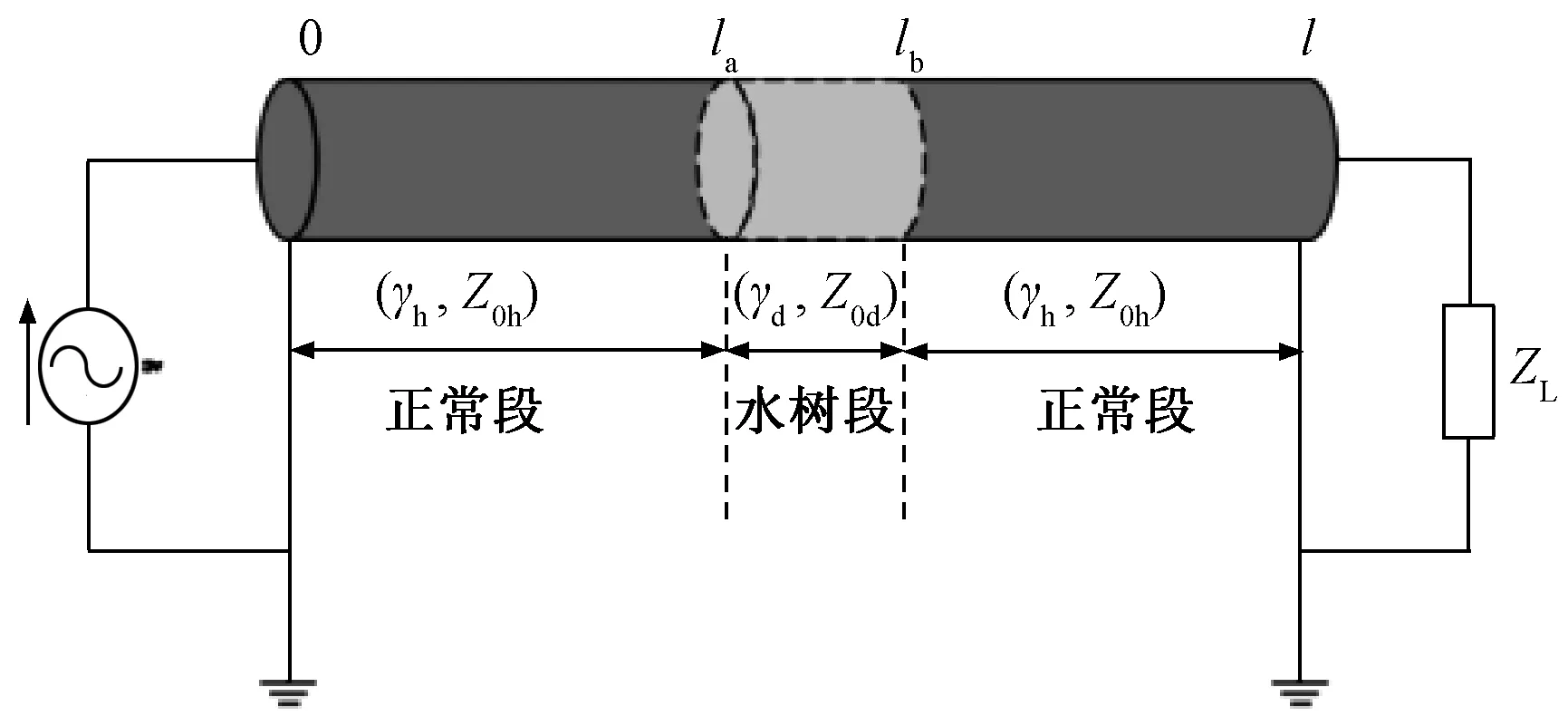
图2 含水树缺陷电缆示意图Fig.2 Water tree defect cable diagram

(10)

(11)

(12)

(13)

(14)

式中，γh和γd分别为电缆正常段的传播常数和水树段的传播常数。

由式(3)可知，当电缆中存在水树缺陷时，缺陷处绝缘介质的复介电常数将发生变化，导致水树缺陷段单位长度电容C发生相应的变化，分布参数C的变化通过影响传播常数和特征阻抗，从而影响电缆首端反射系数谱。

由式(9)可知首端反射系数谱的实部与虚部具有相似性，且均能独立反映反射系数谱的特性。图3分别为三根测试电缆的首端反射系数谱实部幅频图，三根电缆均为长度50 m的同一型号电缆。其中第一根未处理，第二根对距首端15 m部分加速水树老化240 h，第三根整段浸泡水中1 h后擦干表面模拟整段受潮。从图3中可以看出首端反射系数谱具有周期性和衰减性，而水树缺陷会影响它的周期性和衰减性，使得谐振频率下的电缆反射系数在发生缺陷前后出现剧烈变化。可见反射系数谱对水树缺陷十分灵敏，利用反射系数谱的这一特点可以实现对水树缺陷的定位和评估。

图3 不同缺陷程度电缆首端反射系数谱对比Fig.3 Reflection coefficient spectrum of several cables with different water tree defects

3 电缆水树缺陷定位

3.1 基于广义正交法的水树缺陷定位原理

在数学中，当两个函数存在广义正交关系时，其乘积的积分结果在不同情况下具有明显差别，利用这一性质可以从首端反射系数谱中获取水树位置ld。由式(10)～式(14)可知，电缆首端反射系数谱Γ(0)是含有缺陷特征和缺陷位置的函数，其性质主要由exp(-2γhlh)和exp(-2γdld)和两个特征算子决定，因此建立如式(15)的转换函数F(x)：

(15)

式中，Γ(0)为电缆首端反射系数谱；K(x)为构建的转换核函数；fup和flow分别为积分频率上、下限；a1和a2分别为正常区域(x≠ld)和水树区域(x=ld)的转换结果；αh和βh分别为正常段衰减常数和相位常数。

工程应用中，αh和βh可以利用网络分析仪测量原始电缆线路或与待测电缆同一型号的电缆在末端短路和开路情况下的首端输入阻抗谱ZSC和ZOC后，通过式(16)计算获取[20]：

(16)

本文所构建的核函数K(x)中因子cos(2βhx)与反射系数谱Γ(0)两者存在广义正交关系。当在缺陷处x=ld时，由于缺陷处的相位常数βd与正常段x≠ld相位常数βh不同，使得在缺陷处的积分变换结果a2与正常段的积分变换结果a1出现了明显差异。因子exp(2αhx)用于消除由反射系数谱带来的衰减特性，使得转换结果F(x)只与缺陷状态相关，而与电缆长度和缺陷距首端距离无关。通过将电缆中正常电缆的相位常数βh与任意位置x处的相位常数βx逐一对比，便可以获取缺陷处的位置信息，从而实现缺陷定位。图4为一根50 m电缆(25 m存在水树缺陷)的转换结果，可见完好电缆除了在电缆末端以外没有明显峰值，而缺陷电缆在25 m处多出一个峰值，反射系数谱经过式(15)转换后，其转换函数F(x)将在缺陷处出现一个峰值。

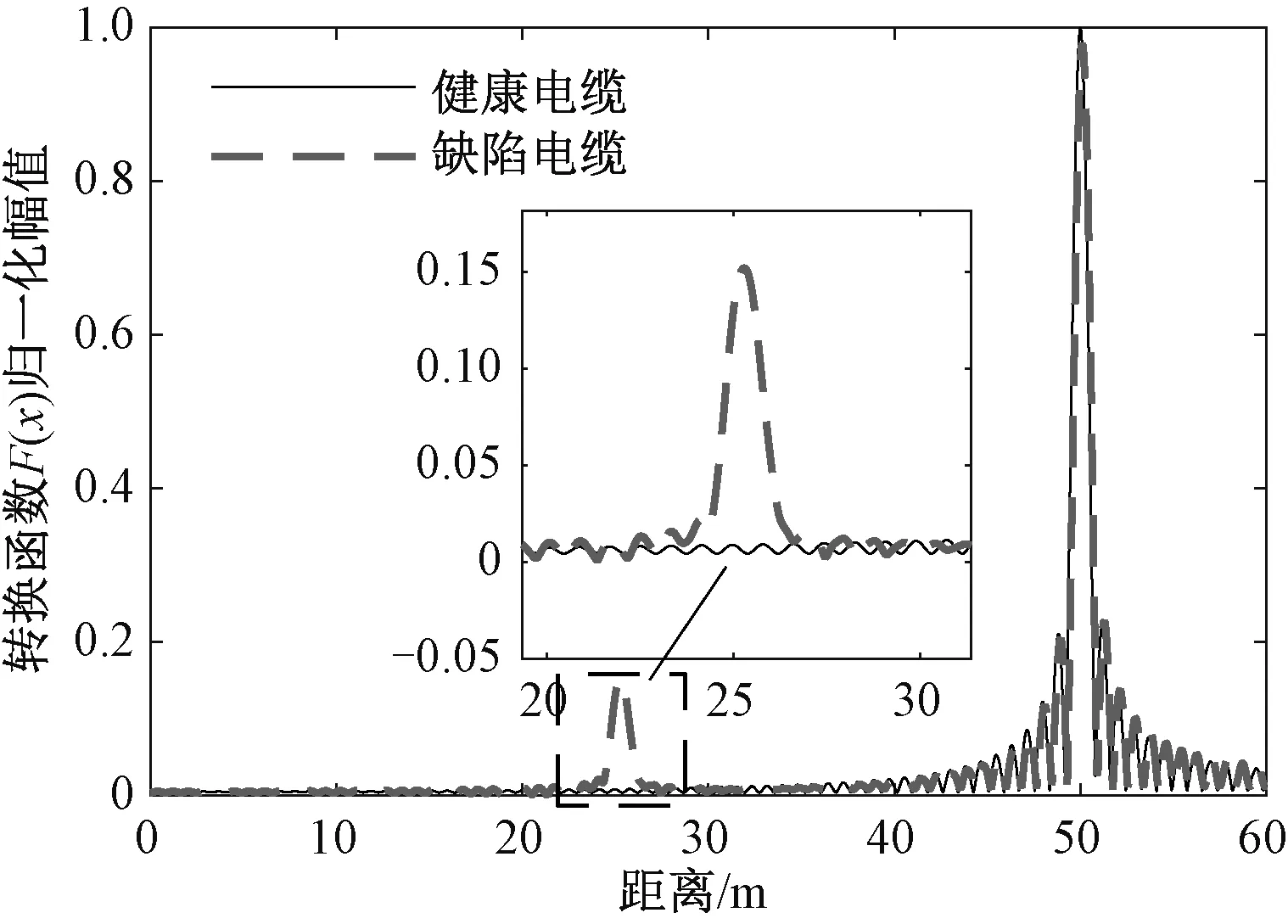
图4 一根50 m电缆F(x)转换结果(25 m处为缺陷位置)Fig.4 F(x) transformation results of 50 m long cable with defection at 25 m

为了更加清晰直观地定位电缆水树缺陷，并表征水树老化缺陷程度，定义诊断函数D(x)为：

D(x)=|Fh(x)-Fd(x)|

(17)

式中，x为与电缆首端距离；Fh(x)为正常电缆的转换谱图；Fd(x)为含有水树缺陷电缆的转换谱图。

在实际应用中，Fh(x)可以通过测量同型号正常电缆或者利用式(15)仿真获取，Fd(x)则可以通过测量待测电缆直接获取。因为诊断函数D(x)定义为电缆健康状态与水树缺陷状态下积分变换的差值，因此当诊断函数D(x)接近0时，说明电缆该位置没有水树缺陷。

3.2 水树缺陷与分布电容的关联特性

为研究水树的类型和尺寸对电缆分布电容的影响，本文在COMSOL Multiphysics 5.5中建立YJV 8.7/15-150电缆模型，利用AC/DC模块下电流场(ec)接口仿真并计算不同情况下水树的电容值。仿真中利用椭球体结构分别建立发散型和领结型水树的等效模型[21]。以图5中外导型水树(从外半导电层开始生长的发散型水树)为例说明仿真模型。如图5所示，水树椭球中心O位于绝缘层与内半导体交界处，长轴b与电场方向平行，纵横比为5，文献[22]指出该值具有良好仿真效果。在水树椭球内设置了诸多充水微孔，充水微孔为一系列长轴为5 μm、短轴为3 μm的椭球体。相邻充水微孔通过长10 μm，宽3 μm的水树通道连接成为“珍珠串”模型，该模型模拟了实际观测到水树所具有的树枝状形态。同时为模拟水树的非均匀性，本文水树部分材料设置采用线性参数，即水树参数从起始点(椭球中心O)到水树与XLPE绝缘交界处呈线性降低(交界处参数与XLPE相同)，仿真中各部分相关材料参数设置如表1所示。

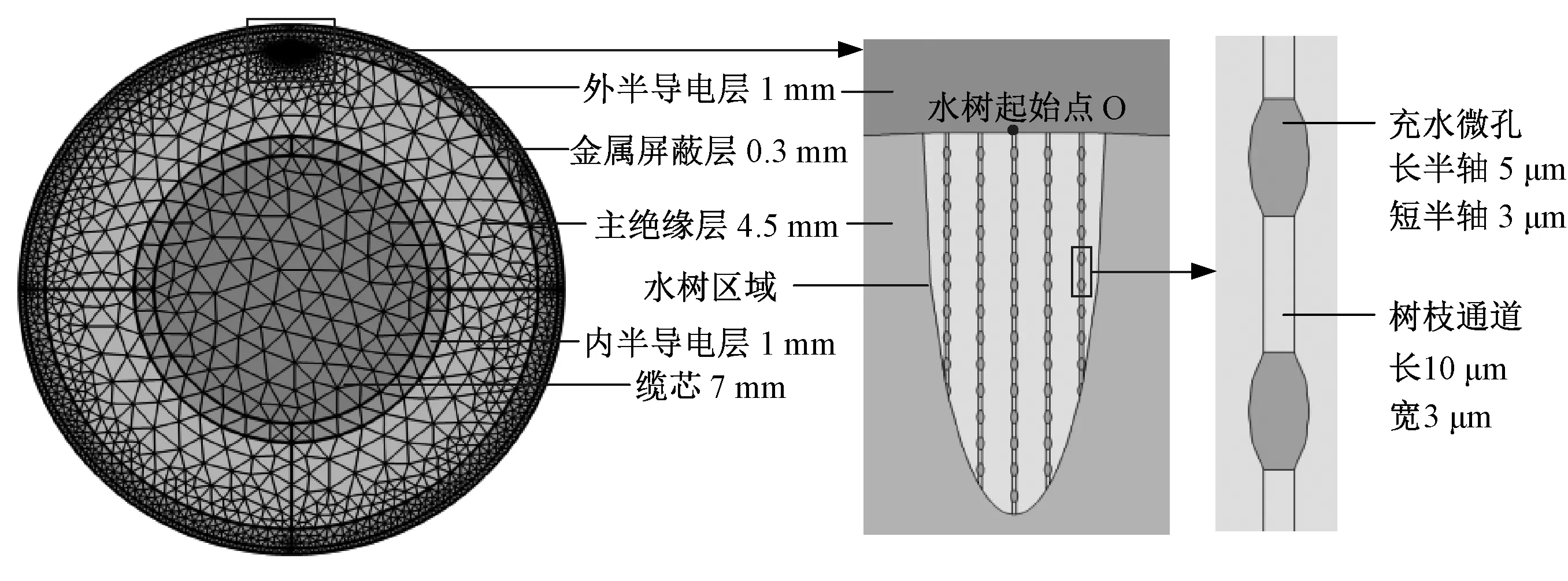
图5 水树有限元仿真模型Fig.5 Water tree finite element simulation model

表1 仿真参数设置Tab.1 Simulation parameters setting

仿真中以10%绝缘层厚度为步长逐渐增加水树尺寸，分别对三种类型的水树进行研究，共得到31组电场和电容结果。图6显示了水树尺寸分别为20%绝缘厚度(长度0.9 mm、短轴0.18 mm)和60%绝缘厚度(长度2.7 mm、短轴0.54 mm)时，三种水树类型的电势和电场分布。如图6所示，水树会使绝缘层电势分布情况发生改变，使水树区域的电场发生畸变，且局部场强较正常区域变大，因此造成水树持续生长直至绝缘击穿。正常电缆中的电势和电场均匀分布，绝缘性能良好；当水树生长至20%绝缘厚度时，水树对电场的影响不是很明显，不足以造成击穿，水树缓慢生长；当水树尺寸达到60%绝缘厚度后，水树已经对电场的分布造成了显著影响，水树快速生长，绝缘击穿场强降低，这与文献[3]的试验结论相符。

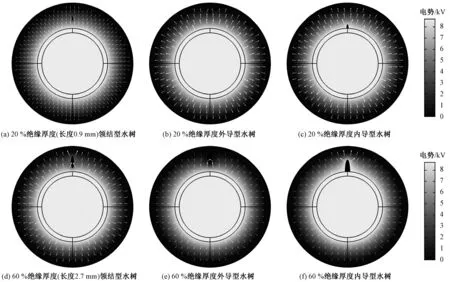
图6 不同类型和尺寸(长度0.9 mm和2.7 mm)水树缺陷下的电势和电场分布Fig.6 Distribution of voltage and electric field under different types and sizes (length 0.9 mm and 2.7 mm) of water tree defects

通过改变水树尺寸刻画水树缺陷程度，获得电容随水树尺寸变化曲线如图7所示。随着水树尺寸的增长，三种类型水树的分布电容呈非线性增长，且增速逐渐加快。同一尺寸下，从内导型水树对分布电容的影响最大，领结型水树对分布电容的影响最小，表明内导型水树的危害性最大。正常电缆的分布电容C0为286.71 pF，当水树发展到绝缘厚度20%时，领结型、外导型、内导型三种类型水树的分布电容分别增长为1.003C0(287.47 pF)、1.004C0(287.80 pF)、1.008C0(288.96 pF)；当水树发展到绝缘厚度60%时，三种类型水树的分布电容分别增长为1.029C0(295.1 pF)、1.047C0(300.3 pF)、1.074C0(308 pF)；可见水树尺寸与分布电容呈正相关，因此可以利用分布电容表征水树老化程度。

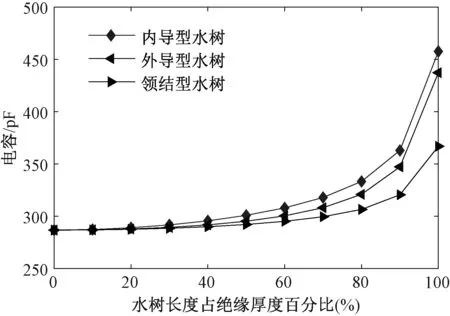
图7 水树缺陷对分布电容的影响Fig.7 Impact of water tree on distributed capacitance

4 水树定位及诊断仿真研究

4.1 仿真设置与诊断结果

本文以10 kV XLPE电力电缆为例进行水树诊断仿真实验，验证本文方法的有效性，仿真电缆结构和尺寸如图8所示。单位电阻和电感分别通过式(1)和式(2)计算。电缆介质的复介电常数通过Cole-Cole模型描述，其表达式如式(18)所示[23]。

图8 10 kV电缆同轴结构Fig.8 Coaxial structure of 10 kV voltage cable

(18)

式中，τ1和τ2为弛豫时间；σdc为直流电导率；A1和A2为幅值系数；ε∞为相对介电常数的高频分量；α1和α2为弛豫峰的广度。

文献[23]利用该模型对测量结果进行拟合，得到电缆各层介质复介电常数表达式，拟合结果如该文献中表2所示。将结果代入式(3)中即可得到电缆单位长度导纳。仿真中正常电缆的传播常数和特征阻抗分别通过式(5)、式(6)计算获得。

仿真中共设置了7个含有水树的电缆样本，仿真频带范围为200 kHz ～ 80 MHz，具体参数设置如表2所示。其中，基于3.2节的研究结果，缺陷程度分别根据20%绝缘厚度尺寸和60%绝缘厚度尺寸下内导型水树的分布电容选取。诊断函数D(x)通过式(17)计算。

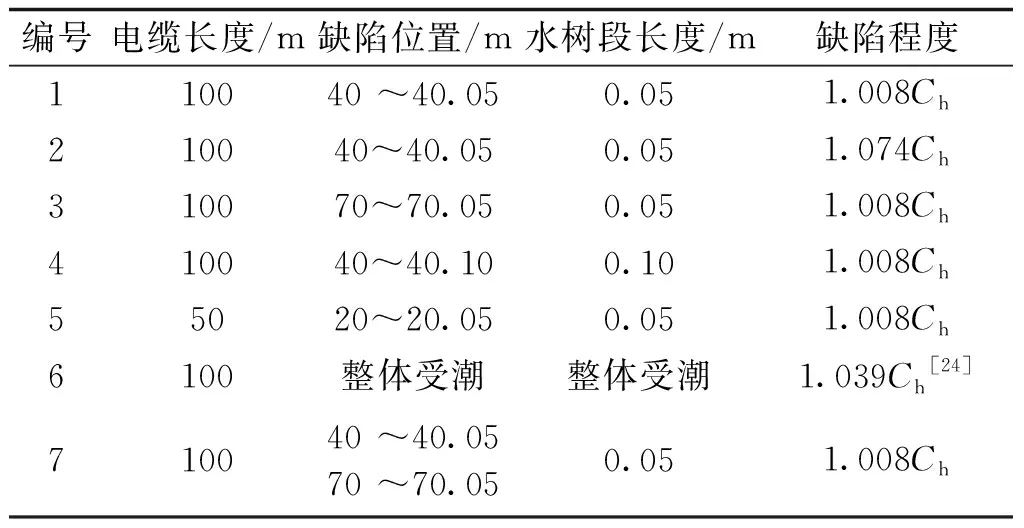
表2 电缆仿真样本设置Tab.2 Simulation specimen of deficient cable

7个样本的仿真结果整理在图9中，首先所有样本中的水树都被准确定位，最大定位误差小于0.1%，定位结果统计见表3。其次因为样本2的水树老化程度较样本1更严重，所以在40 m处样本2的诊断峰值大于样本1，说明诊断函数峰值与水树老化程度呈正相关。样本3与样本1相比仅改变了水树位置，然而两个样本在对应缺陷处的峰值几乎相等，说明诊断函数峰值几乎不受水树位置影响，也就是说除了电缆末端诊断盲区，电缆其余位置的水树都能被有效检测。样本4与样本1相比仅有水树区域长度不同，而在40 m处样本4的诊断函数峰值明显高于样本1，说明诊断函数峰值受水树区域长度影响。样本5与样本1为两根长度不同的电缆，而两个样本在对应缺陷处的诊断函数峰值几乎相等，说明诊断函数峰值独立于待测电缆长度，即只改变待测电缆长度不会影响诊断结果，因此本文方法可以应用于长电缆的水树定位。样本6设置为整段电缆因长期受潮而导致水分侵入整段电缆，此时诊断函数峰值仅在电缆末端出现，但其余位置的值却会远大于0，因此本文方法不仅可以诊断局部水树也可以诊断整体受潮。样本7为电缆中同时出现多处水树的例子，各处水树均被准确定位，此外样本7中两处水树与样本1和样本3中对应位置的诊断结果有略微差别，这是由70 m和40 m两处水树之间的相互折反射现象导致的，但比较两个样本的诊断结果可知，这种多次折反射现象对诊断结果的影响十分微弱，因此应用本文方法时可以忽略多处水树之间的折反射对诊断结果的相互影响。

表3 水树诊断结果Tab.3 Diagnose results of water trees

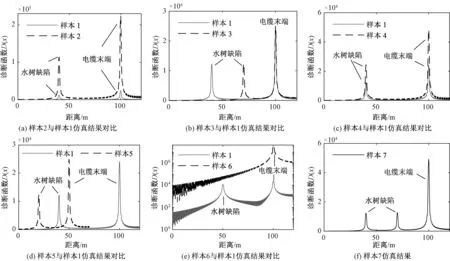
图9 水树诊断仿真结果Fig.9 Simulation results of water tree diagnosis

4.2 负载类型的影响

在电缆末端开路的情况下，所提方法可取得较好的诊断效果，而针对实际应用时负载可能无法切断的情况，需要明确电缆负载类型对所提方法诊断结果的影响。对一根长度为500 m的电缆(水树设置在200 m处)进行仿真研究，其末端分别接入感性负载(ZL=10+j5ω)和容性负载(ZL=5 000-j10/ω)时的诊断结果如图10所示。两种负载类型下水树缺陷均被准确定位，在感性负载下的诊断峰值为3 192，在容性负载下的诊断峰值为3 261，两次诊断效果几乎一致。因此，负载类型对所提方法的诊断结果影响可以忽略。

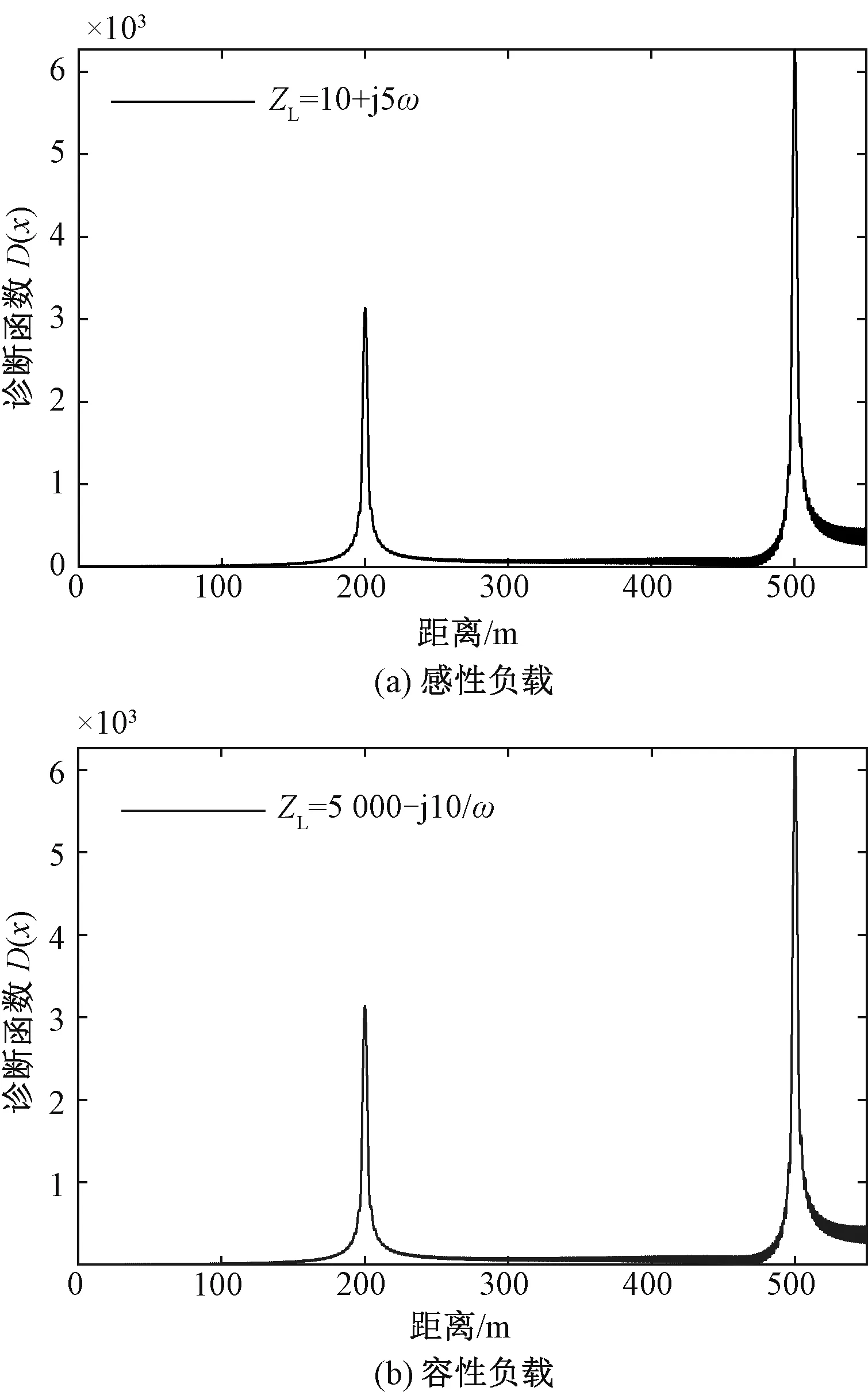
图10 不同负载类型下的诊断结果Fig.10 Diagnosis results under different load types

4.3 最佳测试频率范围

由式(15)可知，频率范围会影响诊断结果，接下来探究频率范围对诊断结果的影响机理，随后确定最佳测试频率范围选取方法。本文方法基于传输线理论，要求线路满足要求l> 0.1λ，其中l为电缆长度，λ为入射信号波长，其定义为：

(19)

故测试频率的下限取值需满足：

(20)

式中，v为电缆波速，一般在1.5 × 108～ 2.2 × 108m/s范围内，本文模型中v的计算值为1.627 × 108。

为探究频率上限对诊断结果的影响规律，对一根长度为500 m的电缆(水树设置在200 m处)，改变测试频率的上限值fup，获得诊断结果与测试频率上限fup的关系如图11所示，每个测试频率范围内水树均被准确定位。定义峰值因数K[25]：

图11 频率上限对诊断结果的影响Fig.11 Influence of upper frequency on diagosis results

(21)

式中，VPeak为诊断函数D(x)突峰值；VRMS为D(x)有效值。

峰值因数K刻画了诊断突峰的凸显程度，即K值越大，诊断突峰越容易被识别，诊断灵敏度越高，诊断结果越直观。一般情况下由于电缆末端阻抗不匹配程度最高，诊断函数会在电缆末端处出现一个较大的突峰，并伴随着产生众多纹波。当K值趋近于0时，此时水树处的突变峰将被临近末端处的纹波淹没，电缆大部分区域成为诊断盲区。工程应用中，一方面希望诊断函数峰值尽可能大，这有利于减小背景干扰和提高水树突变峰的识别成功率。另一方面希望峰值因数K尽可能大，这有利于缩小诊断盲区和提升诊断直观性。然而从图11可以看出，随着频率上限的增加，虽然水树处诊断函数的峰值增加，但K值却在超过40 MHz后逐渐降低，甚至在100 MHz时趋近于0，因此需要选取合适的测试频率才能获得最佳诊断效果。

上述现象是由反射系数谱随频率的衰减性造成的。图12显示了算例中反射系数谱随频率的变化关系，可见反射系数谱随频率的增加呈指数型衰减，当频率超过40 MHz后，其值几乎趋近于0。积分变换法的定位本质是从出现水树前后反射系数谱的变化量中获取水树信息，由于过高频率下反射系数谱本身幅值很小，导致出现水树前后谱图变化量也非常小，因此该部分频谱对水树的敏感程度很低，也就是说超过某一阈值后的频率部分会对诊断结果起到削弱作用。综上所述，为保证本文方法的高效性，需避免使用反射系数幅值过小的部分，本文确定幅值的阈值为0.01，则测试频率的上限fup取值可由式(22)确定：

图12 反射系数谱与频率的关系Fig.12 Relationship between reflection coefficient spectrum and frequency

|Γ(0)|=e-2αfupl≥0.01

(22)

由于衰减系数α正比于频率，所以上限频率fup随着电缆长度l增加而降低，6 km电缆对应的fup为2.21 MHz。总的来说，测试频率范围会影响诊断结果，利用式(21)～式(23)确定的最佳测试频率范围将获得最佳诊断效果，不需要较高测试频率以及对于长电缆所需测试频率进一步降低都是本文方法的优势。

4.4 待测电缆长度

尽管4.1节中已经说明了待测电缆长度不影响诊断结果，但由式(21)～式(23)可知，最佳测试频率范围与待测电缆长度有关，而测试频率范围会影响诊断结果。为探究待测电缆长度对诊断结果的间接影响，设置了一系列长度为l的电缆，并在电缆距首端l/2处设置长度为10 cm的水树区域，且每根电缆均根据式(21)～式(23)采用最佳测试频率范围。测试诊断结果与待测电缆长度的关系如图13所示，可知诊断峰值随着待测电缆变长而降低，这是因为电缆变长后水树区域对首端反射系数谱的影响变小，使得诊断效果变差。当电缆长度达到2.5 km后轻度水树的峰值低于103，考虑到环境干扰和测量误差，此时检测灵敏度较低，水树突峰无法有效识别。然而重度水树的峰值在6 km之前仍高于103，可以有效识别。

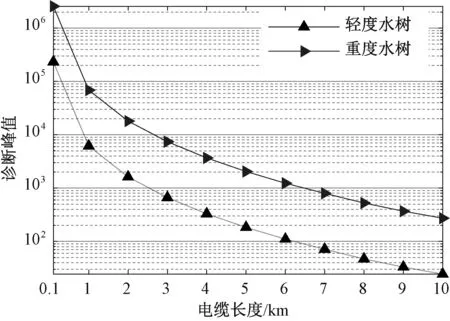
图13 电缆长度对诊断结果的影响Fig.13 Influence of cable length on diagnosis results

综上所述，本方法最大有效检测电缆长度与水树缺陷情况有关，算例表明能够可靠定位2.5 km电缆中的轻度水树以及6 km电缆中的重度水树，两个算例对应的频率上限分别为6.63 MHz和2.21 MHz。

4.5 电缆接头对诊断结果的影响

考虑到实际中电缆接头处的分布参数与本体不同，可能导致误诊的情况，需要有效区别诊断结果中的突变峰值是由接头还是水树缺陷导致的。文献[24]利用有限元方法获取了电缆接头处的分布参数，图14显示了含中间接头电缆的水树诊断仿真结果，可见在接头位置均出现突峰，水树接头与正常接头突峰值有明显差异。由于本文方法诊断结果的突峰不随距首端距离变化而改变，所以正常电缆接头与水树缺陷相比其突峰位置和突峰幅值都具有稳定性。对于新建电缆线路，可以在投运前测量获取其原始特征数据Fh(x)，后期检测结果与之对比即可。而对于在运电缆线路，则可以将测试结果与仿真结果进行对比，或者按以下步骤逐步排查：①对于初次测试的结果，观察结果中出现的多个突峰，将其中突峰值几乎相等的位置标记为电缆接头，并保留测试结果。②若存在突峰值特别高的位置可以认为存在严重水树，建议立即治理。③将当前测试结果与前一次测试结果对比，突峰新增或改变的位置则可以确诊为水树。由于水树的生长是一个缓慢的过程，且水树初期对电缆绝缘性能的影响很小，所以只要定期检测，就一定能及时发现电缆潜在危险，保证电网安全运行。

图14 含中间接头电缆的水树诊断仿真结果Fig.14 Water tree diagnosis simulation results of cables with middle joint

4.6 诊断灵敏度分析

本文方法对于不同情况的水树缺陷，其诊断效果存在差异。为进一步探究该方法的诊断灵敏度，利用仿真模型，在一根100 m电缆距首端40 m处设置了一系列不同长度和老化程度的水树区域，采用最佳测试频带仿真。诊断灵敏度通过式(22)中峰值因数K表征量化。

仿真结果如图15所示，可以发现缺陷长度和缺陷程度均影响该方法诊断灵敏度，其中缺陷长度的影响更加显著。随着缺陷长度的增长，该方法的诊断灵敏度逐渐降低；当水树区域长度小于1 m时，随着水树程度的增加，其诊断灵敏度缓慢提升，而当水树区域长度大于1 m时，随着水树程度的增加，其诊断灵敏度缓慢降低。总的来说，对于区域长度小于2 m的缺陷，该方法具有良好诊断灵敏度。此外，根据图9中样本6的仿真结果可知，所提方法也可以诊断出电缆整段劣化缺陷。

图15 不同程度水树诊断灵敏度Fig.15 Diagnosis sensitivity of different water tree condition

5 实验与讨论

5.1 诊断试验水树样本电缆制作及参数获取

为了验证本文所提出方法对水树诊断的有效性，在实验室利用水针电极法[26]在一根50 m长的型号为YJV 8.7/15-150同轴电缆距一端15 m和35 m制作两处水树缺陷。首先制作15 m处水树并加压240 h，随后制作35 m处水树再继续加压240 h，即35 m处水树加压总时长为480 h，15 m处水树加压总时长为240 h。所加电源电压7.5 kV，频率800 Hz。在进行加速水树老化试验之前利用网络分析仪(E5061B)测量了老化前电缆的首端反射系数和传播系数，获取积分变换所需的特征参量。在加速老化试验结束后用铜网覆盖其表面，测量老化后电缆首端反射系数谱，过程中以矢量网络分析仪接入端为电缆首端，同时保持测试电缆末端开路。利用式(21)～式(23)确定最佳频率范围为输入信号源的频率范围为0.4～120 MHz，测量频率点数为1 000，图16为测量平台示意图。由于网络分析仪为BNC接口，需要对电缆终端进行预处理，以满足连接需求。制作一根长约1.5 cm的含BNC接头的电极，对应连接至电缆屏蔽层和电缆芯线。

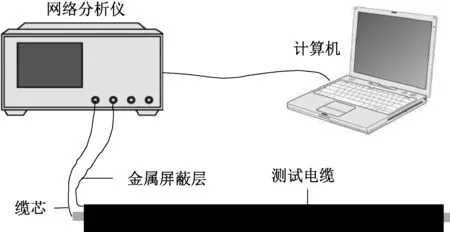
图16 首端反射系数谱测量平台示意图Fig.16 Schematic diagram of head end reflection coefficient measurement platform

5.2 诊断试验结果

将首端反射系数谱代入式(15)～式(17)获得诊断函数D(x)。诊断结果如图17和表4所示，可以看到诊断函数D(x)在15.055 m和35.034 m处出现两个明显峰值，两处缺陷均被准确定位。35.034 m处的峰值大于15.055 m处，表明35.034 m处的老化程度高于15.055 m处，诊断结果与试验设定相符。

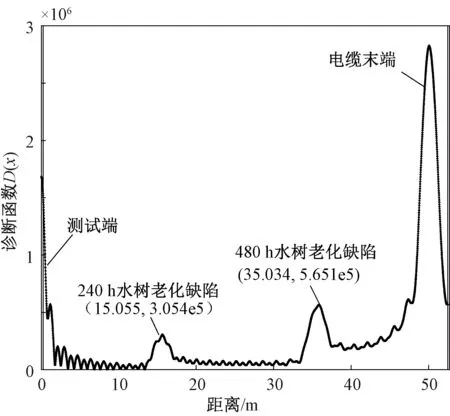
图17 水树诊断试验结果Fig.17 Diagnose experiment results of water trees

表4 水树诊断试验结果Tab.4 Diagnose experiment results of water trees

由于电缆首端延长电极和末端开路造成的阻抗不匹配，在电缆首端和末端处均出现了一个“遮蔽区域”[16]，较文献中的测试结果该“遮蔽区域”有了较大改善。可见根据式(21)～式(23)采用最佳测试频带后可以大幅度削弱电缆端部的“遮蔽效应”，而工程应用中还可以通过特制测试转换端口，进一步降低首端阻抗不匹配带来的影响。

定位测试结束后将水树部分切片(0.2 mm)，然后将薄片浸泡在亚甲基蓝溶液中24 h，使水树充分染色，通过光学显微镜观察到如图18所示的典型水树形态。水树区域形似椭球，纵横比较低，加速老化240 h后长半轴238 μm、短半轴149 μm，加速老化480 h后发展至长半轴675 μm、短半轴433 μm。

图18 加速水树老化试验水树形态Fig.18 Water tree shape by accelerated experiment

试验测试结果验证了本文方法的有效性，该方法不仅能够针对电缆中多处水树情况进行精确定位，定位误差小于0.4%，而且诊断函数峰值与水树老化程度正相关，能够有效反映水树老化程度，可以作为水树缺陷程度表征量，为电缆线路的状态诊断提供有效信息。

6 结论

(1)本文提出了一种基于反射系数谱的水树定位方法，该方法以水树缺陷引起的电缆分布电容变化为特征量，利用广义正交法分析电缆首端反射系数谱，获取缺陷位置和状态信息，能够有效应用于同时存在多处水树缺陷情况的诊断。

(2)利用有限元法研究水树类型与尺寸对电缆分布电容的影响，发现水树使分布电容变大。相同尺寸下，领结型水树、外导型水树和内导型水树的分布电容依次增加，三种类型水树的分布电容均随着水树尺寸的增长呈非线性增长。

(3)通过仿真和实验验证了该方法对水树缺陷诊断的有效性和准确性，结果表明本文方法对于同时存在多处水树缺陷的电缆，不仅能够精确定位各水树位置，定位误差小于0.4%，满足工程应用需求，而且诊断函数D(x)峰值与水树老化程度正相关，能够作为评估水树老化程度的新特征量。

(4)给出了应用该方法时最佳测试频率范围的选取方法，实验结果显示采用最佳频带可以有效削弱电缆终端阻抗不匹配造成的“遮蔽效应”。测试频率上限与电缆长度负相关，算例中2.5 km电缆所需频率上限仅为6.63 MHz。与一般FDR法[14]相比，获得良好定位效果所需的测试频率明显降低，对于长电缆的诊断具有明显优势。