基于并联GABP与NSGA-Ⅱ的微铣削子午线轮胎模具侧板工艺参数优化

张杰翔 李志永 张 伟 刘俨后 宋 山 李 越

(①山东理工大学机械工程学院，山东 淄博 255049；②山东豪迈机械科技股份有限公司，山东 高密 261500；③山东省轮胎模具关键技术重点实验室，山东 高密 261500)

子午胎相对于斜交胎有较多的优点，如节省原材料、减振性能好、耐磨性能好、抓地力好，运动升温低、使用寿命长等[1]。其中子午线轮胎模具侧板上的各种字体，各种认证号及标识都是该轮胎的身份证明，是轮胎花纹的重要组成部分。微铣削技术是加工子午线轮胎模具侧板刻字与标识的重要技术，但在加工过程中刀具的磨损会导致切削力的剧烈增加，造成几何精度与零件质量的下降，高刀具破损率使成本无法预测，加工时间效率低下[2-3]。

杨学明[4-5]等通过微细铣削黄铜H59试验，发现每齿进给量、轴向切深、主轴转速和径向切深对刀具磨损的影响依次减小。Xian Wu[6]等对PCD微立铣刀在碳化钨微铣削加工中的刀具磨损进行了试验研究。结果表明，PCD刀具磨损集中在刀尖处，刀具底部形成三角形磨损带表面。Vipindas K[7]等研究了TiAlN涂层硬质合金刀具在Ti-6Al-4V微铣削过程中的磨损行为,指出每齿进给量-刀刃半径比对微端铣削加工机理有重要影响。程宏林[8]研究了陶瓷坯体微细铣削加工中预测刀具磨损率的理论模型，确定了刀具磨损的主要形式是磨粒磨损。Manso C S[9]等研究了在H13工具钢微铣削过程中，刀具磨损对刀具直径的影响,指出低的每齿进给水平和主轴速度导致较高的刀具磨损，总直径减少22%以上。Móricz Lászlí[10]等基于人工神经网络的特征选择方案，确定了微铣刀磨损阶段与测量的在线和离线参数之间的关系。Amin Dadgari[11]等研究了碳化钨微端铣刀在钛合金Ti-6Al-4V上进行槽铣削时的磨损情况，指出高切削速度和低进给率可以降低刀具磨损率，提高刀具寿命。

上述研究只揭示了切削参数对刀具磨损的影响规律，并没有考虑加工过程的能耗。微铣削刀具直径小，加工过程中主轴转速极高，刀具磨损严重，需要更多的能源消耗。刀具磨损和加工能耗与工艺参数之间并不存在线性的映射关系，研究微铣刀切削寿命、加工能耗与切削参数的关系，建立精确的多目标优化模型是微铣削加工的必然发展方向。通过优化切削参数，降低刀具磨损，延长刀具寿命，降低加工能耗，提髙加工效率，对实际加工有重要意义。

本文以某型号45#钢子午线轮胎模具侧板为研究对象进行微铣削试验，利用微细铣刀后刀面磨损带面积作为刀具磨损量来衡量刀具的磨损程度，基于并联GABP神经网络构建多目标优化模型，以最小刀具磨损面积、最小切削比能为优化目标，利用NSGA-Ⅱ算法迭代求解获得pareto解集，最终基于灰色关联分析获得最优切削参数组合。

1 试验方案

1.1 试验设备

本试验以山东豪迈机械科技股份有限公司的XK1200四轴数控铣削加工中心为试验平台，通过日置PW3360功率传感器实时采集机床主轴变频器的输入端功率。试验工件为某型号45#钢子午线轮胎模具侧板。微细铣刀如图1所示，具体参数见表1。

表1 微细铣刀参数表

1.2 试验设计

微细铣削刀具直径较小，刚度较低，导致微细铣削时的许用切削力较小，加工磨损严重，能耗消耗较高，这对选取切削参数：切削速度、每齿进给量、切深等产生了限制[12]。结合工厂生产的实际加工经验，子午线轮胎模具侧板铣削试验中主轴转速n、每齿进给量fz、切削深度ap的取值范围及要求如表2所示(三因素四水平)。根据表2，进行43= 64组全试验。每次加工切削行程均为2 m，铣削宽度ae为固定值0.2 mm。

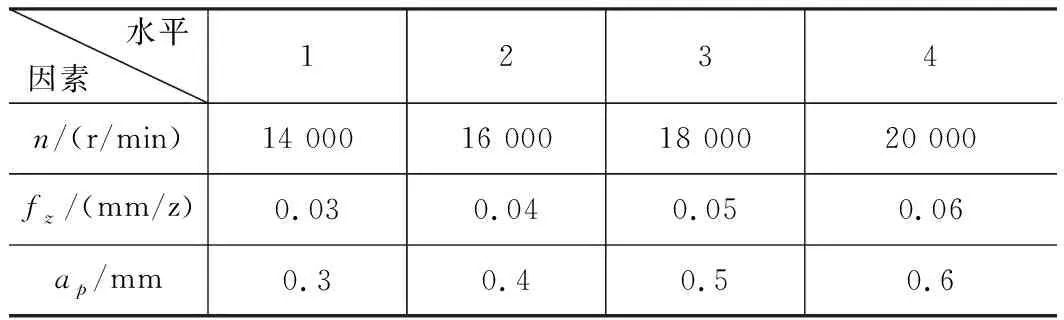
表2 铣削试验切削参数n、fz、ap因素水平表

2 优化目标

2.1 刀具磨损面积

微细铣刀后刀面磨损是影响微铣刀性能的一个重要因素，严重的后刀面磨损会导致刀具迅速破损失效[13]。本文通过微细铣刀铣削子午线轮胎模具侧板试验，提出利用刀具后刀面磨损带面积SVB来衡量刀具的磨损程度的方法，后刀面磨损带面积SVB在计算时即考虑了整个磨损带的变化情况，能同时反应磨损带长度和宽度两个方向的变化。从底刃观察磨损区域可以近似看做为一个三角形，呈白色，如图3所示。

(1)

2.2 切削比能

切削比能即去除单位体积材料所消耗的能量，它能够反映切削能耗与材料去除率之间的映射关系以及机床能效能力[14]。试验中利用PW3360功率计测得机床主轴的实时功率，进而由式(2)计算获得切削比能。

(2)

式中：SCE为切削比能，J/mm3；Pc为加工功率，W；t为加工时间，s；V为去除材料的体积，mm3。

利用64把微细铣刀按照试验方案进行铣削试验，将切削参数n、fz、ap，刀具磨损面积SVB，切削比能SCE记录在表3中。

表3 子午轮胎模具侧板铣削试验结果(部分)

3 并联GABP预测模型

为了更好地研究切削参数和刀具磨损面积、切削比能之间的关系，本文对传统GABP神经网络进行了改进，利用并联GABP神经网络建立了刀具磨损面积与切削比能的预测模型，进一步提高了预测精度。根据表3中的试验结果，选择56组数据(1～56)作为训练样本进行训练，8组数据(57～64)作为检验样本进行检验。

3.1 GABP神经网络模型

BP (back propagation) 神经网络的数学描述为：

(3)

(4)

式中：xj为输入层的输入，wij为连接输入层与隐含层的权值，θi为隐含层神经元阈值，yi为隐含层输出；Tli为连接隐含层与输出层的权值，θl为输出层神经元阈值，Ol为输出层输出。

神经网络具有优异的非线性拟合能力，但存在易陷于局部极小值、预测结果极不稳定，需多次试算才能收敛的缺点[15]。因此本文针对BP神经网络的缺点，利用遗传算法良好的全局寻优能力对BP神经网络的权值和阈值进行优化改进，进而建立高精度的GABP预测模型。GABP神经网络选用3层网络结构。选用主轴转速n、每齿进给量fz、切削深度ap为输入，来预测刀具磨损面积SVB和切削比能SCE，进行单目标预测时，经过多次训练，发现隐含层神经元数为12时，两者预测误差均为最低，所以单目标网络的输入神经元为3，输出神经元为1，隐含层包含12个神经元，即网络结构为3-12-1结构。进行多目标预测时，隐含层神经元数为24时，预测误差最低，则多目标网络结构为3-24-2，结构如图4所示。

3.2 并联GABP神经网络

单目标GABP预测模型在前向计算过程中，隐含层每个神经元权值只需考虑一个输出目标，此时计算获得的权值与阈值，对单一目标的预测精度是最高的。而传统多目标预测模型，隐含层与输出层神经元采用全连接的方式，如图4所示，隐含层的每一个神经元的权值在进行前向计算的过程中，需要同时权衡多个目标，导致多目标预测精度降低。

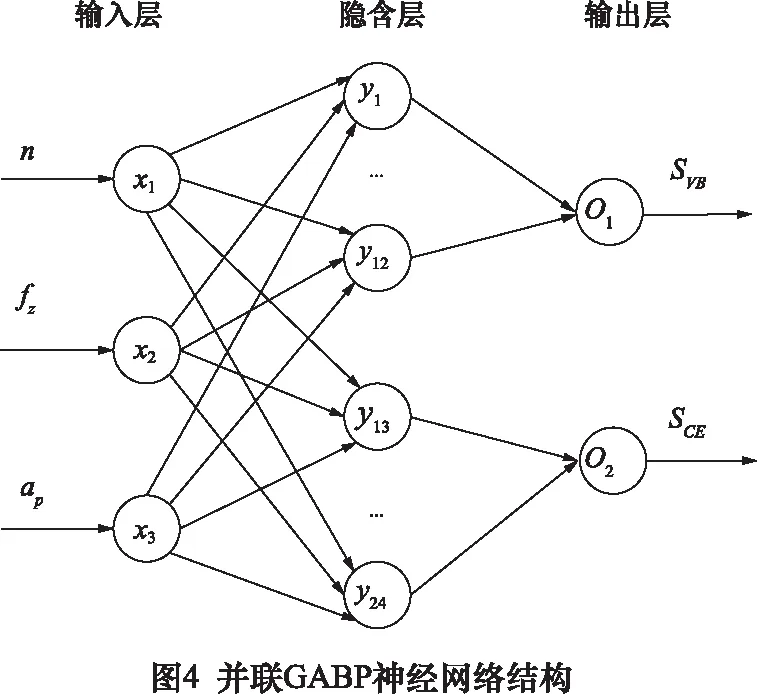
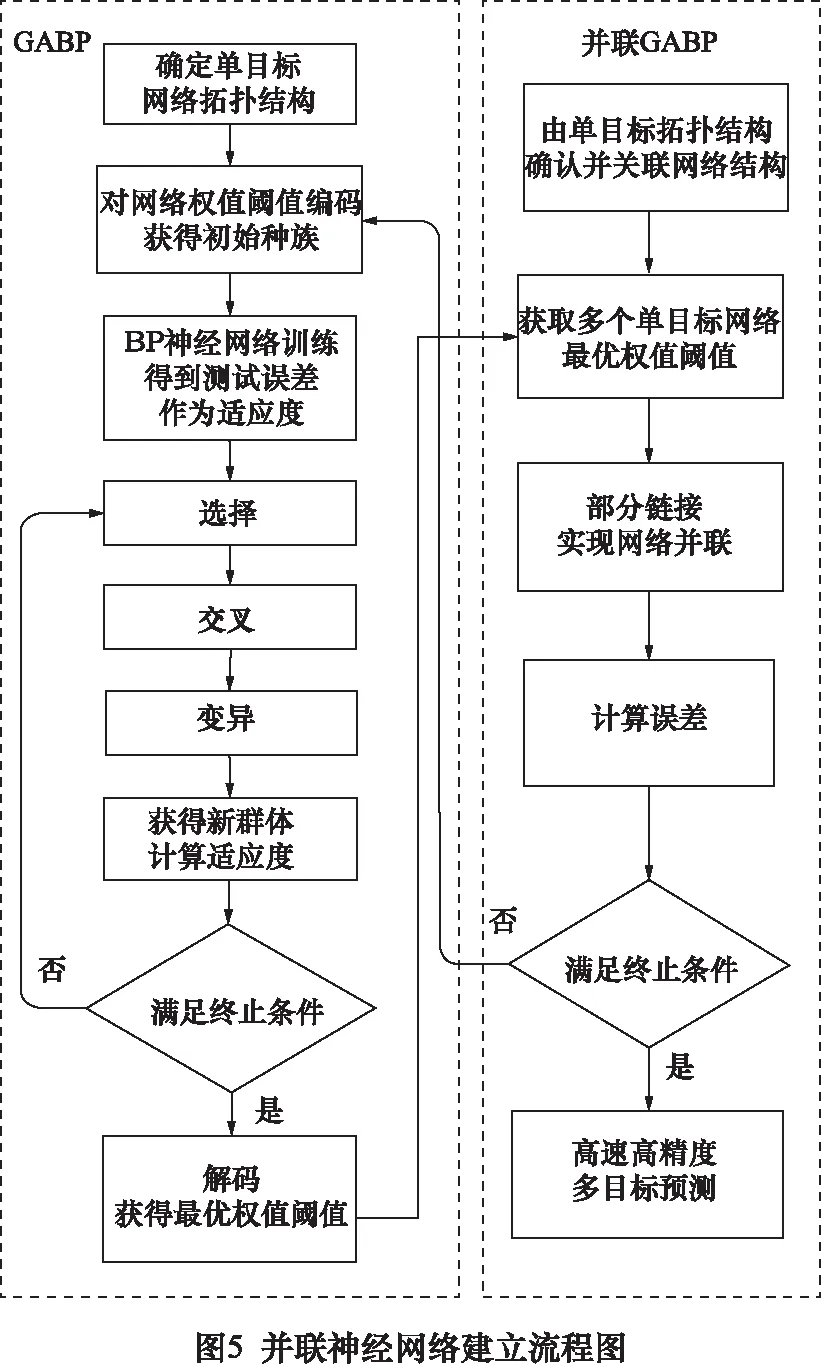
为此对多目标GABP神经网络进行了改进，该网络由两个子GABP神经网络构成，分别建立刀具磨损面积和切削比能的单目标神经网络模型。通过调取上述结构为3-12-1的单目标GABP模型的权值与阈值，赋值给3-24-2的多目标模型，实现了两个单目标GABP神经网络的“并联”，如图5所示。相对于传统的多目标GABP模型，在隐含层与输出层连接方面，采用部分连接的方式简化了神经网络结构，隐含层与输出层的权值数减少了一半。两个子GABP神经网络共用输入，且内部保持了单目标的结构，提高了预测精度。并联GABP神经网络流程如图6所示。

遗传算法优化权值阈值部分参数设置为：最大迭代次数为40次，种群大小为50个，交叉概率为 0.4，变异概率为0.2。神经网络部分参数设置：利用MATLAB的Mapminmax函数对数据进行归一化处理，最大训练次数1 000次，学习率0.1；训练样本期望误差设定为0.000 1。

按照上述参数和步骤，经过训练和多次迭代后，分别建立了并联GABP神经网络和传统GABP神经网络，用8组校验样本试验数据进行检验测试，得到两者误差分布图结果如图7和图8所示，并将误差数值记录在表4中。对比并联GABP神经网络与传统的GABP神经网络的预测误差和，并联GABP神经网络相对于传统GABP神经网络切削比能预测误差和十分接近, 而刀具磨损面积预测误差和减少了40.82%, 进一步提高了多目标神经网络的预测精度。

表4 校验样本预测误差对比

4 NSGA-Ⅱ寻优与灰色关联分析

4.1 NSGA-Ⅱ遗传算法寻优

NSGA-Ⅱ(第二代非支配排序)遗传算法进行多目标优化具有良好的收敛性和鲁棒性，它采用更快速非劣排序，引入拥挤比较算子，使Pareto解在目标空间分布均匀[16-17]。因此本文利用MATLAB基于NSGA-Ⅱ遗传算法的Gamultiobj函数求解该并联GABP神经网络，调用并联GABP神经网络预测的刀具磨损面积与切削比能输出，构造NSGA-Ⅱ遗传算法的适应度函数。

设定迭代次数为300次，种群大小为50个，交叉概率为0.8，变异概率为0.2，适应度函数误差为1×10-10。经300次迭代后得到切削参数的Pareto front最优解集，如图9所示。

Pareto front最优解个数为20个，Pareto front变化趋势表明，刀具磨损面积与切削比能相互抑制，不能同时减小。20组Pareto front最优解及对应的切削参数组合如表5所示。

考虑到预测和优化求解过程中均存在误差，主轴转速范围19 000～20 000 r/min，每齿进给量范围0.037～0.6 mm/z，切削深度0.5～0.6 mm。说明提高主轴转速和切削深度，既有利于降低切削比能又有利于降低刀具磨损面积，而增大每齿进给量会降低切削比能但会增大刀具磨损面积。因此在同时追求高效节能和较高的刀具寿命的要求下，应尽量通过提高主轴转速和切削深度来实现。

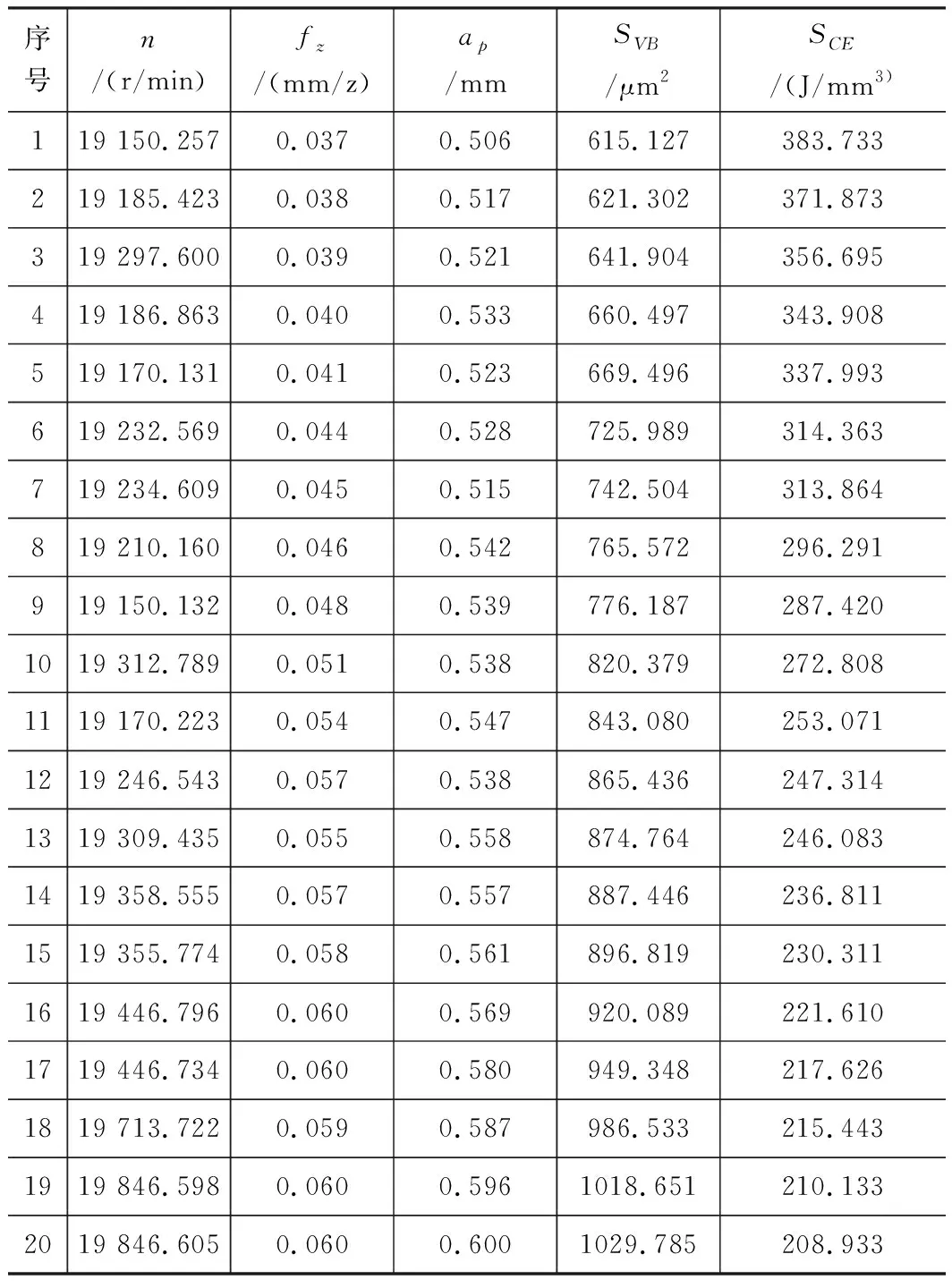
表5 Pareto front 最优解参数

由Pareto解集可以看出，在n=19 150.257 r/min，fz=0.037 mm/z，ap=0.506 mm时有最小刀具磨损面积SVB=615.127 μm2，较64组试验中n=20 000 r/min，fz=0.05 mm/z，ap=0.3 mm时刀具磨损面积SVB=734.4 μm2降低了16.24%。最小的切削比能在最高的切削参数水平组合下取得SCE=208.475 J/mm3。

4.2 灰色关联分析

以上通过并联GABP神经网络与NSGA-Ⅱ优化模型获得了关于刀具磨损与切削比能的pareto最优解集，但还是无法判断出最优的一组工艺参数，为此对试验数据与优化解集进行灰色关联分析寻找最优的一组工艺参数。

邓聚龙[13]教授建立的灰色系统理论是一种重点研究包含部分已知信息的不确定系统的有效方法，由于机械加工是一个包含各种切削参数和加工条件的复杂系统，因此灰色系统理论在机械加工金属切削领域中得到了广泛的应用。

灰色关联分析主要分为3个步骤：数据预处理、灰色关联系数和灰色关联度。

(1)数据预处理

拥有不同量纲的数据无法进行比较。因此，需要对进行灰色关联分析的数据进行无量纲化处理。由于在优化过程中，刀具磨损面积与切削比能都是越小越好，因此进行原始序列“望小”处理，如式(7)所示：

(7)

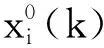
(2)关联系数

采用预处理后的序列，灰色关联系数计算如式(8)所示：

γ(x0i(k))=

(8)

式中：ζ为分辨系数，ζ∈(0，1]。一般取0.5。

(3)灰色关联度

试验中数据为多个时，需对不同序列的关联系数进行加权求和，如式(9)所示。

(9)

式中：pk表示第k列比较数列的权重系数，关联度ri越大，越接近最优解。本文认为降低刀具磨损面积与切削比能同等重要，因此p1=p2=0.5。

对原始试验数据和Pareto优化解集共84组数据进行灰色关联分析排序，按照上述步骤进行数据处理后，计算获得具体灰色关联度如表6，最优切削参数组合为n=19 185.423 r/min，fz=0.038 mm/z,ap=0.517 mm,

SVB=621.302 μm2,SCE=371.873 J/mm3。

5 结语

本文通过微细刀具铣削某型号子午线轮胎模具侧板进行试验，重点研究了微铣削加工过程中切削参数组合对刀具磨损面积和切削比能的影响规律并进行了预测，利用NSGA-Ⅱ多目标优化算法对并联GABP神经网络进行了优化求解，并进行灰色关联分析，主要结论有：

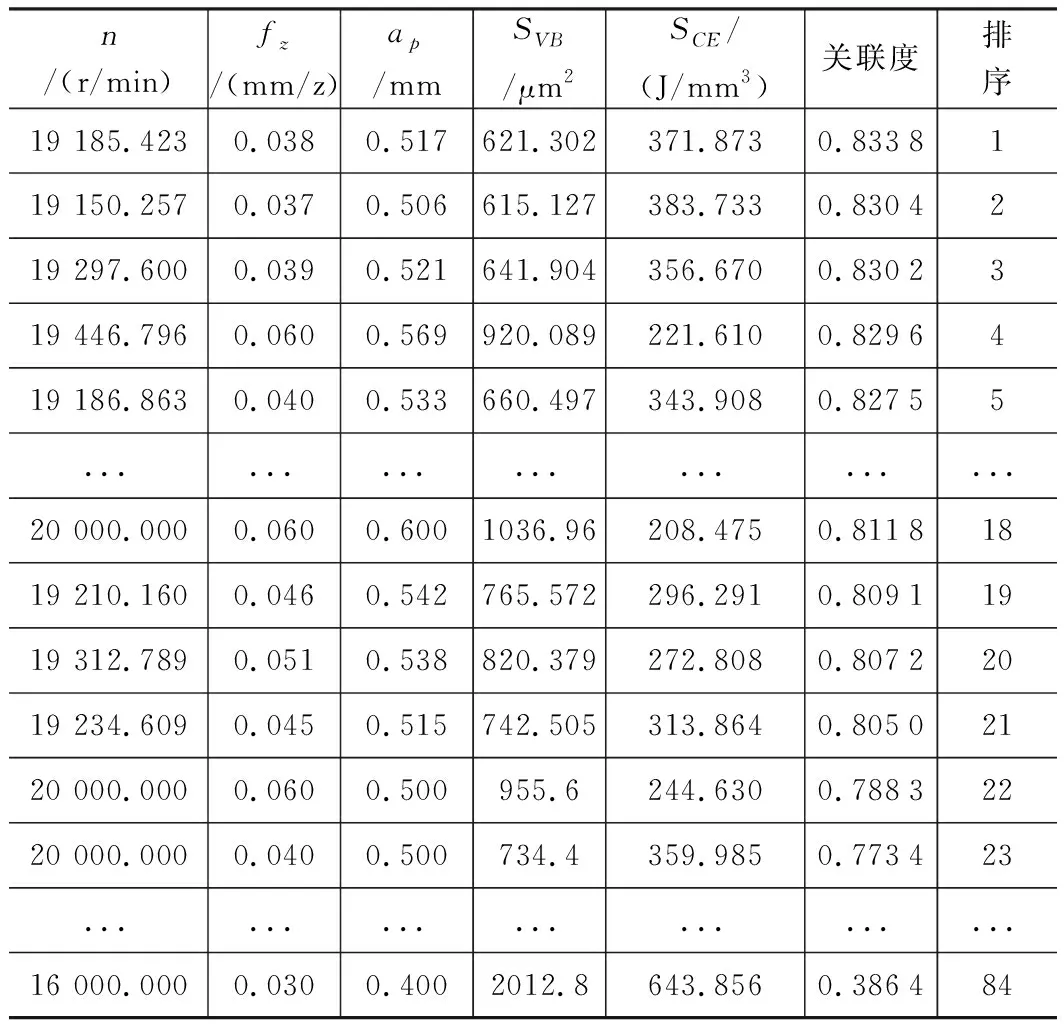
表6 灰色关联度排序表(部分)

(1)对传统多目标GABP神经网络进行了改进，根据试验结果，建立了输入量为主轴转速、每齿进给量、切削深度，输出量为刀具磨损面积和切削比能的并联GABP神经网络模型，刀具磨损面积预测误差较传统多目标GABP神经网络减少了40.82%。

(2)通过NSGA-Ⅱ对并联GABP神经网络模型进行参数优化求解，获得20组pareto解，供企业选择。主轴转速范围19 000～20 000 r/min，每齿进给量范围0.037～0.6 mm/z，切削深度范围0.5～0.6 mm。对试验结果和优化结果进行了灰色关联分析，获得了最优的一组工艺参数：n=19 185.423 r/min，fz=0.038 mm/z,ap=0.517 mm,SVB=621.302 μm2,SCE=371.873 J/mm3。

(3)提高主轴转速和切削深度既有利于降低刀具磨损面积又有利于降低切削比能。而增大每齿进给量会降低切削比能但会增大刀具磨损面积。在兼顾刀具磨损与切削比能的情况下，推荐选择较高的主轴转速、切削深度和较低的每齿进给量。