刀具螺旋槽磨削接触线的几何求解及其在三维建模中的应用

曾 滔 刘战强 左小陈 罗 胜

(①山东大学机械工程学院，山东 济南 250100；②株洲钻石切削刀具股份有限公司，湖南 株洲 412007)

刀具三维建模是刀具数字化设计技术的一项重要内容，螺旋槽是旋转类整体刀具的共有特征，精确地建立螺旋槽的三维实体模型对于提高刀具设计开发效率具有重要意义。

螺旋槽结构设计与磨削加工中，有一条重要的特征线称为磨削接触线，它是砂轮作螺旋运动时，任意时刻砂轮与螺旋槽之间的瞬时相切线。接触线绕砂轮轴线旋转，得到砂轮的外圆周面；绕刀具轴线作螺旋运动，得到刀具螺旋槽。由于接触线同时具备砂轮和螺旋槽的特征信息，如果能求解出螺旋槽磨削接触线，在三维设计软件中将其绕刀具轴线作螺旋运动，便可精确建立螺旋槽的三维实体模型。

目前建立刀具螺旋槽三维模型的方法主要有3种。一是“截面扫掠法”，即利用三维设计软件的“扫掠”功能，将螺旋槽横截面轮廓沿指定螺旋线扫掠生产螺旋槽[1-2]。这种方法原理和操作都非常简单，应用非常普遍，但最大的问题是螺旋槽的截面轮廓通常仅用3个设计参数进行描述，与实际产品的截面轮廓存在一定误差，而且螺旋槽槽尾即砂轮退刀处无法实现精准建模，故建模的精度不高。二是“实体切除法”，即利用某些三维设计软件(如SolidWorks)中的特定功能，使砂轮实体沿指定路径作螺旋运动形成包络体，然后与刀体作布尔减运算形成螺旋槽[3-4]。这种方法操作简单，但对三维设计软件的功能有限制，具有一定局限性，而且计算量较大。三是“仿真加工法”，它是基于螺旋槽的磨削加工原理，利用数控加工仿真技术和软件生成刀具实体模型[5-6]。“仿真加工法”所生成的螺旋槽模型理论上与实际产品完全一致，精度非常高，但需要具备扎实的螺旋槽磨削加工理论知识，完成建模的难度较大。

可见，上述方法均存在一定弊端，而且建模过程中未有效利用螺旋槽磨削接触线。造成该现状的原因在于螺旋槽磨削接触线通常基于曲面共轭原理进行求解，这种解析法涉及微分方程[7-8]和复杂的非线性方程[9]，接触线只能用离散的点云进行描述，在三维设计软件中，除非进行二次开发，不然接触线和螺旋槽的建模很难实现参数化。为快捷、高效、精确地建立刀具螺旋槽的三维参数化实体模型，本文提出了一种求解螺旋槽磨削接触线的几何方法，并应用该方法实现了刀具螺旋槽的三维参数化建模。

1 解析法求解磨削接触线

如图1所示，以砂轮左侧大端面圆心为原点建立砂轮坐标系oW-xWyWzW，其中zW轴与砂轮轴线重合，并指向砂轮左端面，xW轴垂直向上。以刀具刃部端面中心为圆心建立刀具坐标系oT-xTyTzT，其中zT轴与刀具轴线重合，并指向刀具刃部，xT轴同样垂直向上，砂轮与刀具坐标系的y轴由右手定则确定。

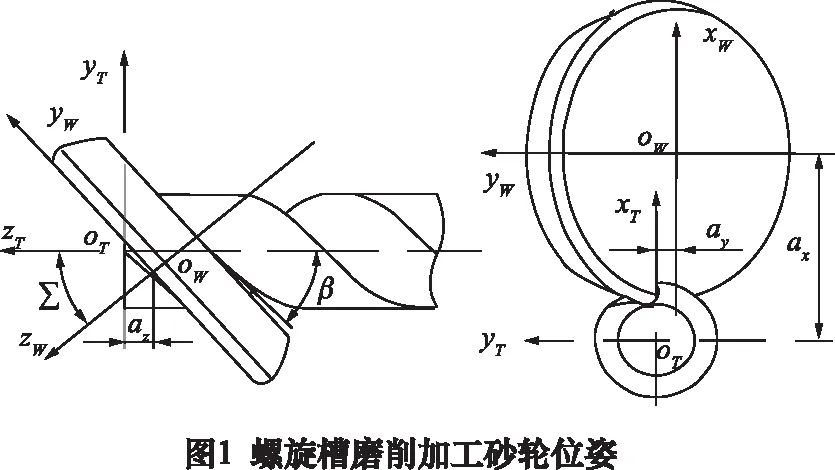
加工刀具螺旋槽时，砂轮相对刀具的初始位姿由4个参数确定：砂轮轴线与刀具轴线间的距离在xT轴上的投影长度ax，砂轮与刀具坐标系原点之间的距离在yT轴上的投影长度ay，在zT上的投影长度az，以及两轴线之间的夹角∑，这4个参数即为螺旋槽磨削参数。其中，参数ax、ay和∑决定螺旋槽的形状，az决定螺旋槽端面截形的周向位置。

确定砂轮相对刀具的位姿后，砂轮绕刀具轴线作螺旋运动，完成螺旋槽的磨削加工。砂轮作螺旋运动的方程如下：

(1)

式中：p=R/tanβ(R为刀具半径)，ε为螺旋运动参数。

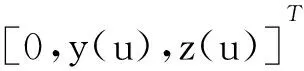
GW(u,α,ε)=

(2)

GW(u,α,ε)表示以螺旋运动参数ε为参变量的曲面族，该曲面族存在包络面S0，S0即为砂轮磨削加工形成的螺旋面。根据曲面共轭条件，

NG·VG=0

(3)

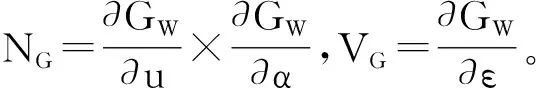
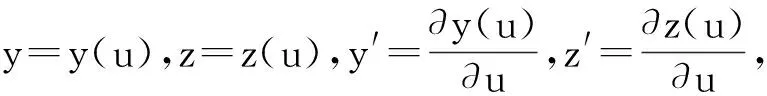
则根据式(2)和(3)，螺旋槽磨削时的曲面共轭条件可整理为

(4)

根据式(4)，可以确定参变量u和α之间的关系，将其代入式(2)中，可求得砂轮在任意加工位置与螺旋槽之间的磨削接触线方程。

2 几何法求解磨削接触线

本文提出的几何法求解螺旋槽磨削接触线是应用目前机械制造行业通用的三维设计软件，借助软件的“曲面求交线”功能获取螺旋槽磨削接触线。

如图2所示，在螺旋运动参数ε=ε0的当前位置，砂轮与螺旋槽之间的接触线为L1，在螺旋运动参数ε=ε0+Δε的临近位置，砂轮与螺旋槽之间的接触线为L2。显然，接触线L2可看作接触线L1作螺旋运动(螺旋运动参数为ε=Δε)形成的新曲线，二者形状完全相同。

当Δε→0时，接触线L2等同于接触线L1，此时，L1上的所有点既在当前砂轮(ε=ε0)上，也在临近位置的砂轮(ε=ε0+Δε)上，即此时接触线L1的近似解是砂轮(ε=ε0)与砂轮(ε=ε0+Δε)的交线。该近似解的精度取决于三维设计软件中，“曲面求交线”功能在可识别两个不同曲面交线的前提下，角度差Δε设定值的大小，Δε越小，接触线的精度越高。从目前的应用情况来看，在UG软件中，Δε值设定为0.005°，甚至0.001°都可求解出接触线，这样的精度完全能够满足工程应用的需求。

由于砂轮任意位置与螺旋槽的磨削接触线空间形状完全一样，根据前文所述极限思想，螺旋运动参数ε=0位置时的磨削接触线满足，

(5)

根据式(2)和式(5)有，

(6)

当螺旋运动参数Δε→0时，sinΔε≐Δε，1-cosΔε=2sin2(Δε/2)≐Δε2/2，高阶无穷小量和无穷小量进行加减运算时，Δε2作为Δε的高阶无穷小量，可以忽略。针对式(6)，通过去除或增加适合的高阶无穷小项P·Δε2(P为函数)，整理可得，

(7)

据式(7)，令y(u1)=g(u2,α2)，z(u1)=h(u2,α2)，当砂轮截形轮廓确定后，y(u1)和z(u1)之间的关系便唯一确定，据此可建立g(u2,α2)和h(u2,α2)之间的关系，即螺旋槽磨削加工时的曲面共轭条件为，

(8)

用于加工螺旋槽的砂轮，不管何种截面轮廓形状，在工程应用中通常都是用多段圆弧或直线光滑连续相接进行拟合。如图3所示的砂轮，若已知其截形轮廓直线段的斜率和截距分别为k、b，任意一个圆弧段的圆心为(xi,yi)，半径Ri，则截形轮廓可用参数方程表示为

对于砂轮截面轮廓直线段，据式(7)、(9)有

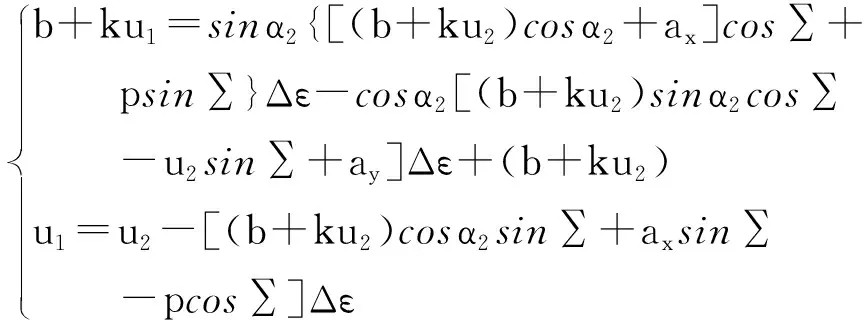
(10)

式(10)消去参数u1整理可得

(11)

对于砂轮截面轮廓圆弧段，据式(7)、(9)有

(12)

式(12)消去参数u1整理可得

(13)

式(11)和(13)分别为采用极限思想推导出的砂轮截面轮廓直线段和圆弧段对应的螺旋槽磨削曲面共轭条件。同样，利用解析法根据式(4)和(9)可推导出曲面共轭条件分别为

(14)

(15)

显然，式(11)与(14)，以及式(13)与(15)在形式上一样，从而证明了基于极限思想的几何法求解接触线具有可靠的数学原理基础。

基于UG、CATIA、Pro/E等三维机械设计软件应用几何法求解刀具螺旋槽磨削加工接触线的具体实施步骤如图4所示：

(1)首先根据目标螺旋曲面的设计参数和加工该螺旋曲面所用砂轮的截面轮廓参数求解砂轮加工螺旋槽的刃磨参数。

(2)根据刃磨参数和砂轮外形尺寸参数，利用三维设计软件在螺旋运动参数ε=ε0位置构造砂轮的三维模型。

(3)利用砂轮模型，抽取ε=ε0位置砂轮的有效加工表面S1。

(4)基于螺旋运动原则，根据有效加工表面S1，利用三维设计软件在ε=ε0+Δε位置构造砂轮有效加工表面S2，其中Δε→0。

(5)选定砂轮有效加工表面S1和S2，利用三维设计软件的“构造曲线交线”功能求出有效加工表面S1和S2的交线，该交线即为螺旋槽磨削接触线。

3 几何法求解接触线的应用

通过一个具体实例，论述几何法求解接触线在刀具三维参数化建模中的应用。本研究应用的三维设计软件为UG，目标刀具为四刃平头立铣刀，其外形尺寸参数见表1。立铣刀三维实体建模的过程依次为：(1)建立刀具棒体毛坯模型；(2)建立螺旋槽模型；(3)建立周刃模型；(4)建立端齿gash模型；(5)建立端齿模型；(6)建立刀尖倒角模型，下文重点论述螺旋槽的三维建模方法。

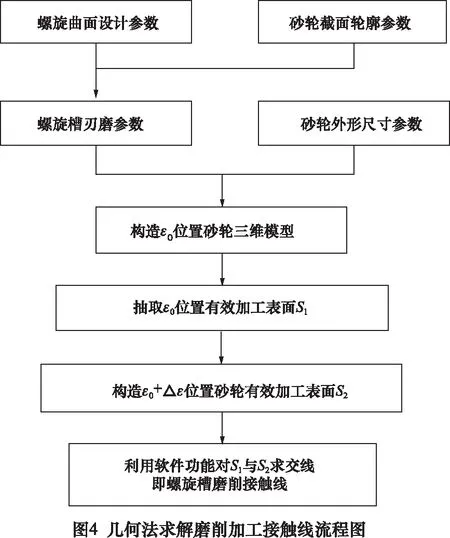
表1 刀具外形尺寸参数

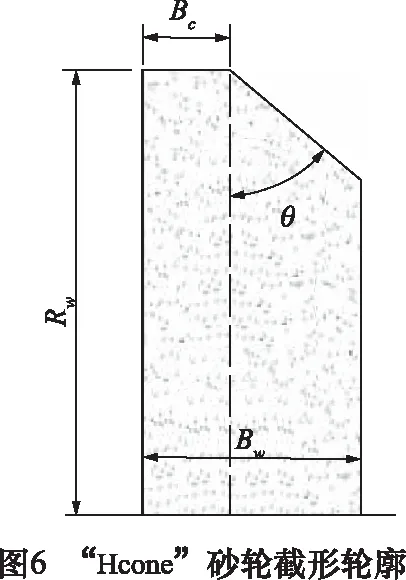
图5所示为铣刀螺旋槽截形轮廓和设计参数示意图，该螺旋槽采用图6所示截形轮廓的 “Hcone”砂轮进行加工；螺旋槽设计参数和砂轮截形轮廓参数值见表2。

(1)构建刀具毛坯和砂轮模型。根据表1数据，建立刀具棒体毛坯模型。根据表2中数据，参考文献[9]中提出的方法推导“Hcone”砂轮加工螺旋槽的刃磨参数求解方程，求解出砂轮刃磨参数为ax=77.917 mm，ay= 4.079 mm，az= 1.778 mm，∑= 41.64°。根据刃磨参数确定砂轮中心，并建立Hcone砂轮三维模型如图7所示。

表2 螺旋槽设计参数和砂轮截形轮廓参数

(2)几何法求解接触线。根据刀具实际加工过程中砂轮外圆周面磨削刀具毛坯的有效范围，在砂轮模型上截取有效加工部分，并抽取当前位置砂轮有效加工表面S。按照螺旋运动规则，利用UG中的“引用几何体”功能，将有效加工表面S沿刀具轴向进行变换，得到ε=ε0位置砂轮的有效加工表面S1。变换参数包括沿轴线转动的角度ε0和沿轴线移动的距离l0，其中l0=lc，ε0=lc/p。同样，利用“引用几何体”功能，将有效加工表面S1沿刀具轴向进行变换，得到ε=ε0+Δε位置砂轮的有效加工表面S2，变换参数为Δε和Δl，其中Δε=0.001°和Δl=pΔε。然后利用“相交曲线功能”，直接求解出S1和S2的交线，如图8所示。

(3)构建螺旋槽槽尾曲面。利用“修剪片体”功能，用接触线将有效加工表面S2的上半部分修剪掉，保留下半部分作为螺旋槽槽尾曲面。

(4)构建螺旋槽曲面。利用“扫掠”功能将接触线绕刀具螺旋刃线扫掠，得到螺旋槽槽体曲面，然后利用曲面“缝合”功能，将槽尾曲面和槽体曲面缝合，得到完整的螺旋槽曲面。

(5)构建螺旋槽实体模型。应用“修剪体”功能，用螺旋槽曲面将刀具棒体毛坯分割，得到螺旋槽实体模型，如图9所示。

(6)最后依次建立周刃、端齿gash、端齿和刀尖倒角模型，完成目标铣刀三维实体模型的建立，如图10所示。

通过检测螺旋槽3个设计参数，间接验证刀具三维模型精度。利用UG中的“测量”功能，对螺旋槽的槽前角、芯径和槽夹角3个设计参数进行检测，检测结果如图11和表3所示。表3显示，3个设计参数的实际误差分别为7.7%、0.16%、0.13%，除槽前角的实际误差稍大外，其他两个设计参数的误差都非常小，但三者的实际误差均显著小于设计误差要求，这表明应用新方法建立的模型精度完全能够满足工程应用需要。

三维模型误差的产生原因主要有两个方面：一是几何法求解磨削接触线导致的误差；二是刃磨参数求解导致的误差，可分别通过减小Δε的取值和提高刃磨参数的求解精度实现减小刀具三维建模误差的目标。

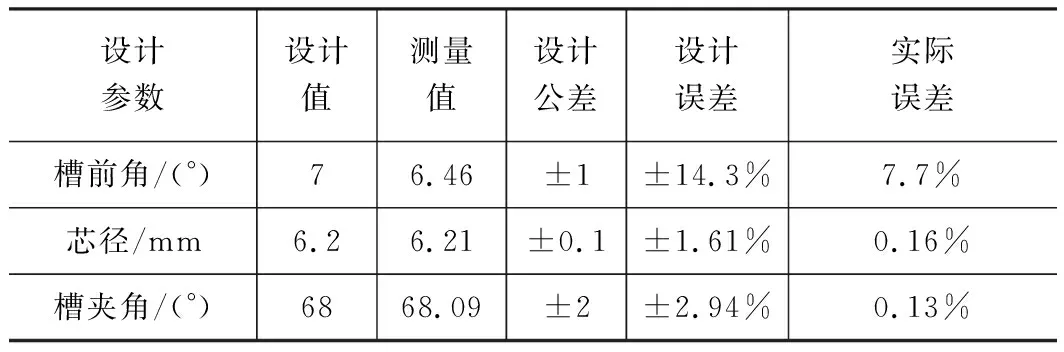
表3 螺旋槽模型实际误差与设计误差对比

4 结语

(1)针对现有螺旋槽三维建模方法未充分利用磨削接触线的现状，以及解析法求解接触线难以在三维软件中实现参数化的弊端，提出一种基于极限思想求解螺旋槽磨削接触线的几何方法。

(2)对几何法求解磨削接触线的的数学原理进行了阐述，将基于极限思想推导的螺旋槽磨削曲面啮合条件与基于包络原理推导的曲面共轭条件进行对比，结果表明二者形式完全一样，证明了极限几何法求解接触线的可靠性。对新方法的具体实施步骤进行了说明。

(3)通过四刃平头立铣刀三维实体建模的具体实例，论述了极限几何法求解螺旋槽磨削接触线在刀具三维建模中的应用。最后对比了螺旋槽设计参数的建模误差与设计误差大小，间接证明了应用新方法建立的刀具三维模型精度完全满足工程需要。