基于斜率模型的突发型黄土滑坡失稳时间预测

2021-07-23方汕澳修德皓赵宽耀李志刚

水文地质工程地质 2021年4期

方汕澳，许强，修德皓，赵宽耀，李志刚，蒲枫

（成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都 610059）

我国西北黄土地区降水稀少、气候干旱，临河地区多采用提水漫灌等灌溉方式，导致地下水位逐渐升高，滑坡等地质灾害频发[1]。由灌溉诱发的滑坡加速阶段历时短、突发性强、危害性大[2]，因此，开展针对此类突发型黄土滑坡的监测预警预报工作对减少人员伤亡和降低经济损失具有重要意义。

已有多位学者针对突发型黄土滑坡监测预警预报展开了研究。亓星等[3]通过研发具有智能变频功能的滑坡位移计成功获取了黑方台地区突发型黄土滑坡完整变形数据；赵超英等[4]、史绪国等[5]多位学者利用InSAR技术实现了黄土滑坡的早期识别和时序监测，提出黄土滑坡监测新方法；亓星等[6−7]先后通过速度倒数法和改进的Saito模型，对突发型黄土滑坡失稳时间预测进行了研究；许强等[8]通过建立以变形速率阈值和改进切线角为预警指标的四级预警判据，成功实现了对甘肃黑方台突发型黄土滑坡的预警，为解决突发型黄土滑坡“什么时间发生”的难题提供了有效途径。

失稳时间预测是监测预警预报工作的重要组成部分[9]，先后经历了现象预测[10−11]、确定性预测、统计分析预测[12−15]、非线性预测[16−18]、确定性预测[19]等几个阶段。确定性预测主要是基于滑坡运动参数，通过物理或数学方法将室内试验数据或滑坡监测数据进行推导，并不断总结改进得到的预测方法，能够反映滑坡的物理实质[19]。Saito等[20]率先通过大量室内试验总结出理想状态下土质边坡失稳时间预测经验公式，并提出了基于蠕变第三阶段的图解法；Fukuzono[21]在室内试验的基础上进一步总结出恒定荷载作用下滑坡临滑阶段位移速度倒数与时间的关系，提出速度倒数法预测模型；Mufundirwa等[22]在前人研究的基础上提出斜率模型（又称SLOPE模型、SLO模型）来表示岩石蠕变末期应变发散特征，并应用到滑坡实例和岩石蠕变试验中。在这之后有多位学者[23−24]基于以上预测模型进行了总结改进。

上述预测方法多应用于室内试验或岩质滑坡，关于自然条件下的黄土滑坡的研究很少，特别是突发型黄土滑坡。本文以2019年黑方台发生的突发型黄土滑坡为研究对象，通过改进的切线角预警模型确定滑坡变形阶段，基于斜率模型提出以切线角为指标的简化计算方法进行滑坡失稳时间预测研究，以期为突发型黄土滑坡的监测预警和应急管理提供一定的建议。

1 研究区概况

黑方台地区位于甘肃省临夏州永靖县内，地貌以黄土台塬、河谷地貌为主。整个台塬由黑台和方台组成，长7.7 km，宽2.5 km，面积为13.7 km2，地势西高东低[25−26]。受常年大水漫灌影响，台塬地下水位以0.3 m/a左右的速率上升，塬边滑坡频发[8]。

据调查统计，黑方台地区发育滑坡多达77处，按发生位置的不同可将该区域滑坡划分为新塬段、党川段、黄茨段、焦家崖段、焦家段和陈家段共六个区段（图1）。从滑坡成灾模式来看，黑方台地区发生的滑坡可划分为黄土基岩型、黄土泥流型、滑移崩塌型和静态液化型滑坡等4类，其中滑移崩塌型和静态液化型滑坡具有明显的突发性特征[27]。2019年成功预警了4起突发型滑坡，主要分布在北侧陈家段和南侧党川段，其中滑移崩塌型滑坡有陈家6#、党川6#和党川7#，静态液化型滑坡有党川4#，具体滑坡预警信息如表1所示。

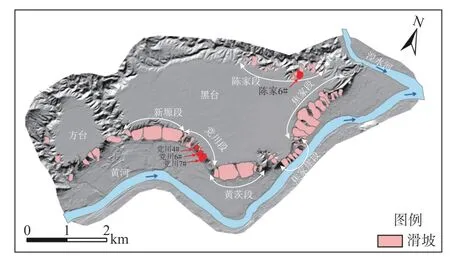
图1 黑方台滑坡分布Fig.1 Location of the Heifangtai landslides

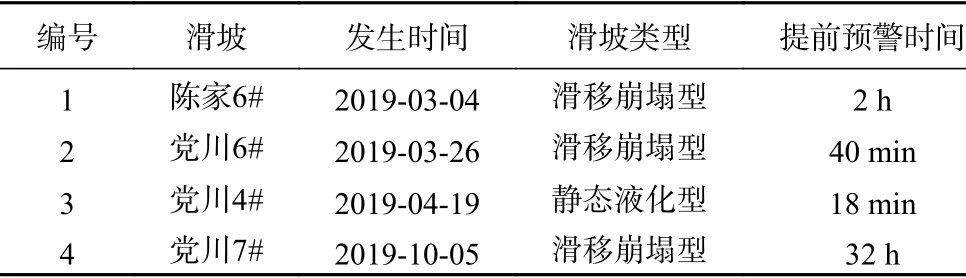
表1 2019年成功预警的滑坡Table 1 Basic characteristics of landslides predicted in 2019

2 研究方法

2.1 监测数据的获取与处理

本文采用具有智能变频功能的滑坡位移计进行位移监测，该仪器能获取突发型黄土滑坡完整变形数据。结合黑方台突发型黄土滑坡的发育规律和特征进行监测仪器的布设（图2）：对于静态液化型滑坡，监测仪器布设在地下水渗水强烈的滑坡后缘附近；对于滑移崩塌型滑坡，监测仪器主要集中在多级裂缝发育的滑坡后缘附近。多次成功预警的案例也验证了上述布设原则的可行性[8]。许强[28]认为当滑坡进入加速变形阶段，滑坡区会以滑动块体形式整体滑动，各监测点的位移矢量方向将趋于一致，选取加速变形阶段不同监测点的监测数据进行预警预报的差别不大。斜率模型是基于加速变形阶段的监测数据进行预测计算，故本文所选取的监测数据能够反映滑坡变形趋势，达到有效预警预报的目的。

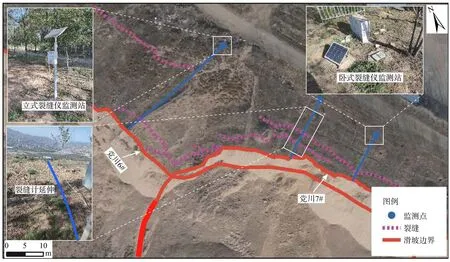
图2 滑坡监测点布设示意图Fig.2 Monitoring systems of the landslides

采用移动平均法对监测数据进行滤波处理，以降低仪器噪声和周围环境对监测数据的影响，反映滑坡变形趋势。计算公式如下：

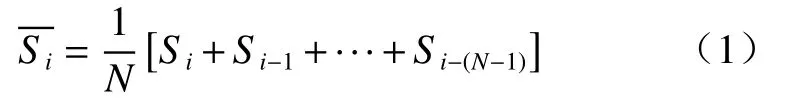
式中：Si—i时刻滑坡的累计位移/mm；

N—移动平均项数；

—移动平均处理后的位移/mm。

处理后的数据预测标准误差大小与N的取值呈正线性相关，N的取值越小误差越小，在这里N取24[8]。

2.2 滑坡变形阶段确定

通过坐标变化进行无量纲处理得到的改进切线角模型能够使滑坡变形曲线在相同切线角特征下进行比较[29]，因此，采用该模型确定滑坡变形阶段，计算公式如下：

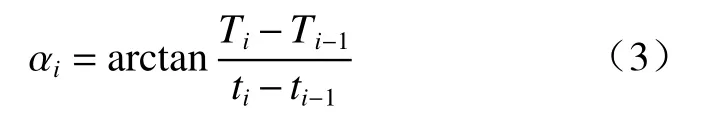
式中：Si—i时刻滑坡的累计位移/mm；

Ti、Ti−1—变换后与时间相同量纲的纵坐标值，两者相差一个监测周期，如1天、1 周等；

—滑坡等速变形阶段的速率/（mm·d−1）；

αi—改进切线角/（°）；

ti、ti−1—监测时刻，两者相差一个监测周期。

当切线角大于45°时，可认为滑坡进入初加速变形阶段；当切线角大于80°时，滑坡进入中加速阶段；当切线角大于85°时，滑坡进入加加速阶段；切线角越接近90°，滑坡越接近发生。突发型黄土滑坡前期变形缓慢且不稳定，切线角存在较大幅度的波动，通过计算发现，当切线角达到60°后，波动性减小且变化趋势较明显，亓星等[7]也指出在滑坡初加速变形阶段（45°～80°）的前期，距离滑坡实际发生时间还较长，较小的波动都会导致预测结果产生较大的差异。故本文以60°切线角为起点，每5°为间隔，将滑坡加速阶段后期划分为60°～65°、65°～70°、70°～75°、75°～80°、80°～85°、85°～90°共6 个变形阶段。

2.3 斜率模型介绍

SLO失稳时间预测模型源于Fukui等[30]根据“加速蠕变理论”总结出的岩石加速蠕变阶段应变与时间关系，见式（4）：

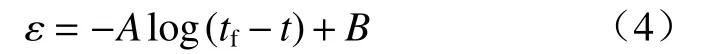
式中：ε—应变；

t—时间/d；

tf—失稳时间/d；

A、B—常数。

Mufundirwa等[22]在式（4）的基础上令滑坡累计位移s代替应变ε，同时式（4）两侧对时间t进行微分，得到式（5），重新整理后得到式（6）。

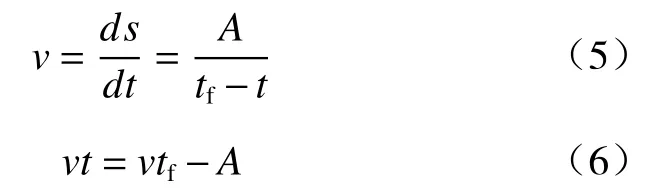
式中：v—滑坡位移速度/（mm·d−1）。

将式（6）中的v·t视作y，v视作x，tf视作斜率，则式（6）转化为以tf为斜率的线性方程，求失稳时间tf也转变为求该方程的斜率k，即求该线性方程的斜率（SLOPE），即SLO预测模型。该模型实质上是速度倒数模型在线性条件下的变形，前提假设为滑坡加速阶段的速度倒数变化符合线性趋势。与其他预测模型相比，该模型将预测失稳时间转化为斜率进行求解，不需要进行复杂的拟合和参数求解，在进行突发型黄土滑坡失稳时间预测方面具有一定的优势。

2.4 预测计算数据选取

斜率模型是基于滑坡加速蠕变阶段提出的，为保证模型适应性和预测结果可靠性，计算数据应从加速变形阶段选取。计算截点的选择对及时判断滑坡危险性意义重大，计算截点过早可能会导致时间预报偏差过大，过晚可能会导致应急处理时间不足。大量成功预警的滑坡案例表明，当切线角达到85°时，滑坡进入临滑阶段，失稳概率极大，此时发布预警预报信息能够有效地指导灾情应急处理工作，降低滑坡造成的经济损失和人员伤亡。因此，为了更好地评估预测结果，本文在进行滑坡失稳时间预测计算时，以各加速变形阶段第一组数据为计算起点，以切线角达到85°为计算截点，采用累计计算的方式进行预测计算（图3）。

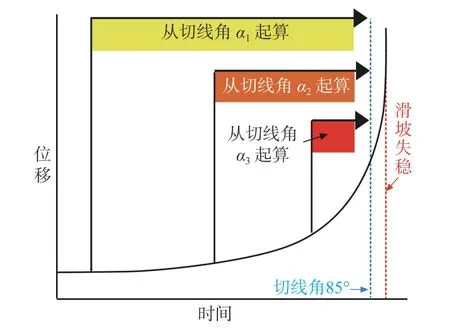
图3 累计计算示意图Fig.3 Schematic diagram of cumulative calculation

但研究发现，由于测量误差、环境变化、滑坡局部滑动和数据处理手段的局限性等多种因素影响，通过监测仪器获得的滑坡变形曲线并不稳定，新数据的增加会对预测结果产生较大的影响，所以本文在累计计算的基础上提取关键变形阶段的数据进行简化计算，只选取滑坡切线角在60 °、65°、70°、75°、80°、85°时对应的监测数据进行累计计算，这既能保证计算数据能反映滑坡变形趋势，又能降低变形波动对预测结果的影响。

2.5 预测结果评价

本文主要采用预测寿命图和预测结果均方根误差（RMSE）从定性和定量的角度进行模型预测结果评价。

预测寿命指的是预测失稳时间与当前预测时间节点的差值，即tfp−tm。预测寿命图以预测寿命为y轴，时间为x轴，能够反映预测结果提前预测、滞后预测、预测失效和预测寿命稳定性等情况（图4）。

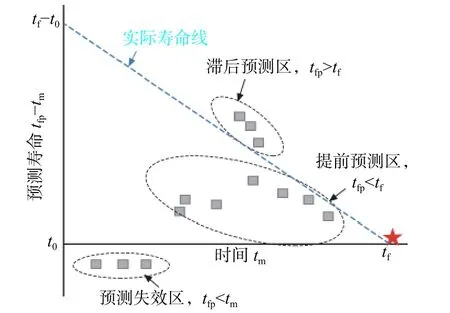
图4 预测寿命图（据文献[22]，有删改）Fig.4 Predicted life expectancy(modified from Ref.[22])

采用均方根误差（RMSE）用来评价模型预测精度，RMSE的值越小，预测精度越高，其表达式如下：

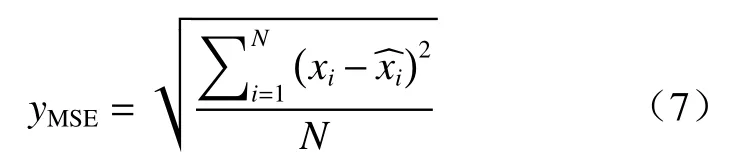
式中：yMSE—均方根误差值；

xi—滑坡实际寿命/h；

N—预测总数。

3 研究结果

3.1 滑移崩塌型滑坡

滑移崩塌型滑坡从发育到发生历时较短，具有明显的突发性特征，但其运动距离和体积较小。滑坡发育与灌溉水关系不大，发育过程主要是坡体在自重和降雨条件下向临空面发生不均匀沉降和变形，在坡体后缘发育有多级裂缝和错台。以党川6#滑坡的预测结果为例进行分析。该滑坡失稳时间为2019年3月26日凌晨5点。通过改进的切线角模型得到滑坡变形曲线（图5），切线角在凌晨4点20分达到85°，进入加速阶段，此时距滑坡失稳还有40 min。

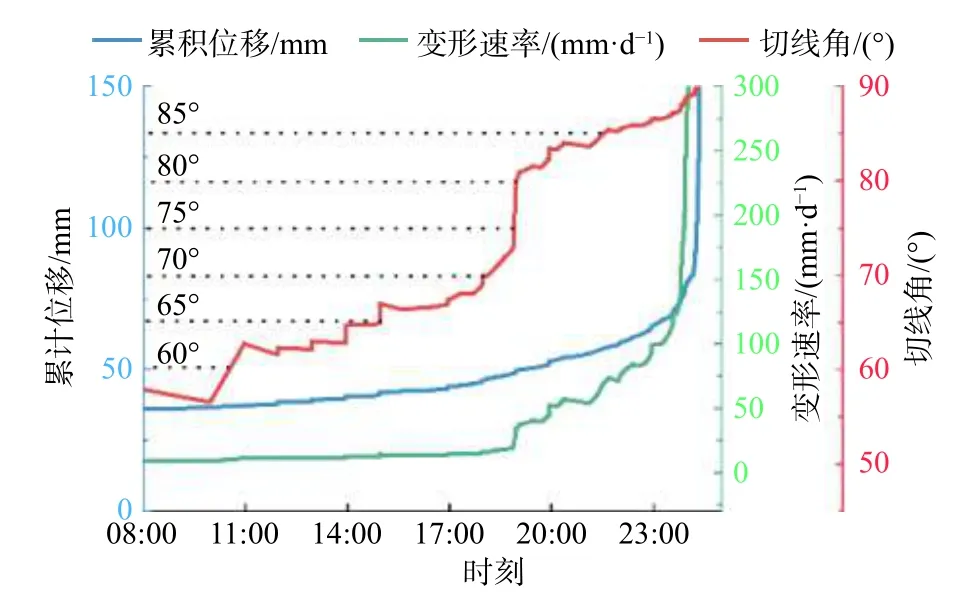
图5 党川6#滑坡变形曲线Fig.5 Deformation curve of the Dangchuan 6# landslide

党川6#滑坡各变形阶段的预测寿命如图6所示，简化累计计算得到的各变形阶段预测寿命波动性较小，变化趋势较平稳，且与实际寿命线变化趋势相近。而累计计算得到的各变形阶段预测寿命波动性较大，在切线角达到80°后，预测寿命变化趋势才趋于平稳。通过计算两种方式得到的滑坡各变形阶段预测结果均方根误差（表2）可以看出，简化累计计算得到各变形阶段预测结果均方根误差均小于0.5 h，预测精度较高。

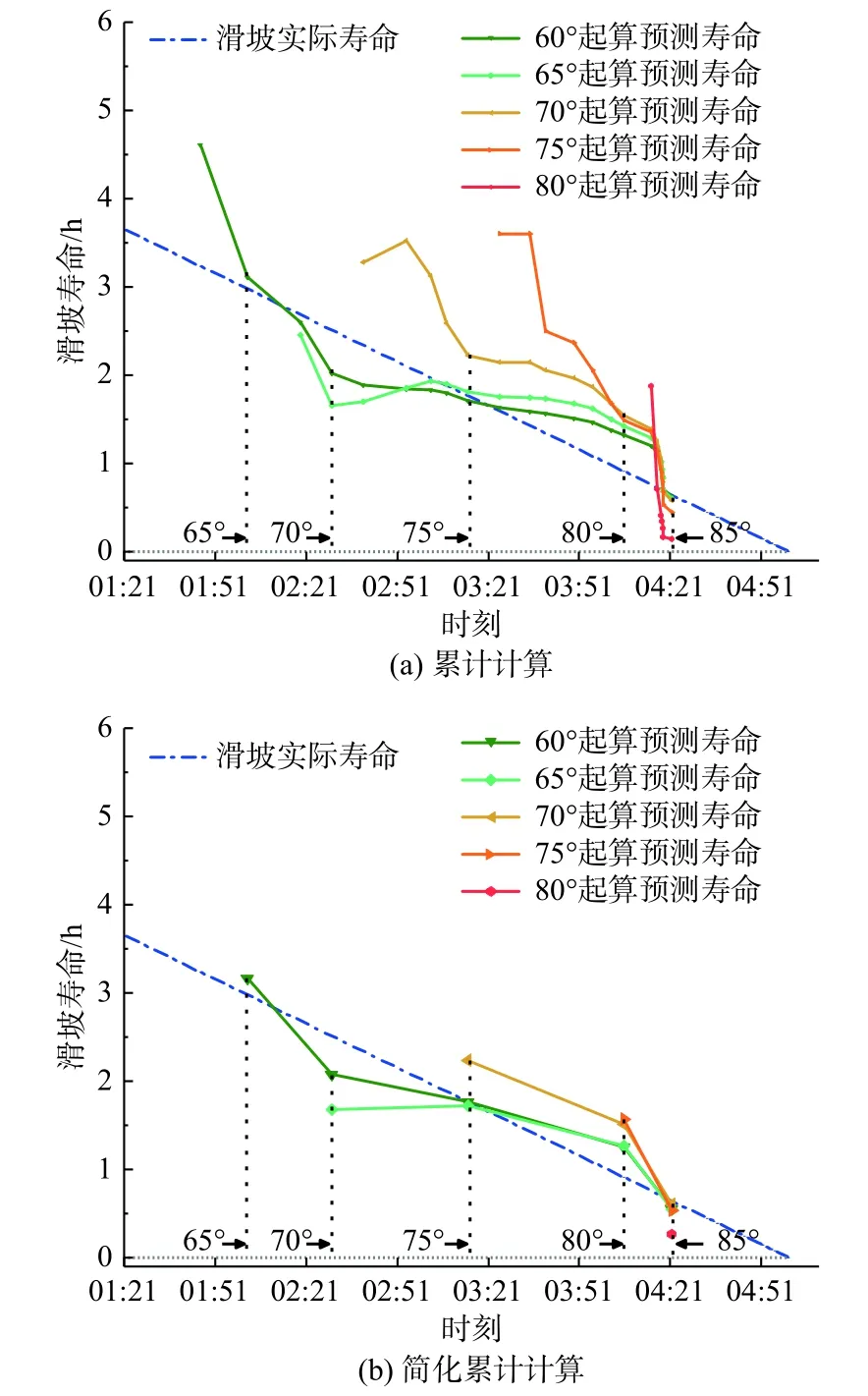
图6 党川6#滑坡预测寿命Fig.6 Predicted life of the Dangchuan 6# landslide

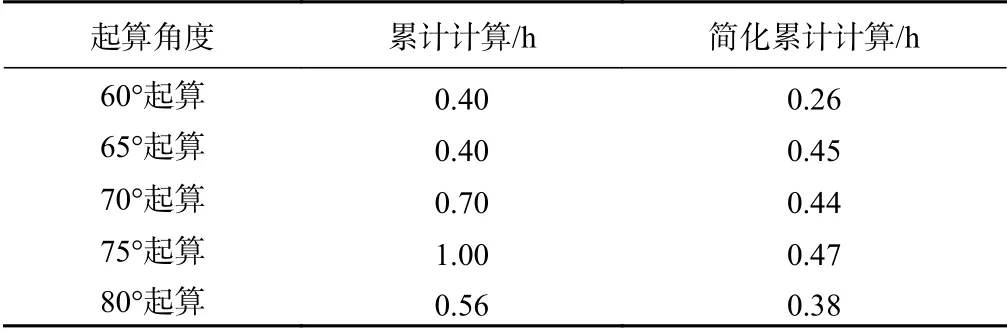
表2 党川6#滑坡预测结果均方根误差Table 2 RMSE of the predicted results of the Dangchuan 6#landslide

通过对比另外两起滑移崩塌型滑坡（陈家6#和党川7#）的预测结果也可以看出（图7）。两种计算方式得到滑坡各变形阶段的预测寿命变化趋势相近，累计计算得到的各变形阶段预测寿命波动性较大，在切线角达到80°后才趋于稳定；而简化累计计算得到的各变形阶段预测寿命波动性较小，变化趋势较平稳，相应的预测结果均方根误差也明显小于累计计算方式，预测精度较高（表3）。其中，党川7#滑坡的预测结果的均方根误差较大，但考虑到预测失稳时间多早于实际失稳时间，且随着起算角度的增加，预测误差逐渐减小，所以斜率模型在党川7#滑坡的预测结果较“安全”。总体来看，斜率模型在滑移崩塌型滑坡中的预测效果较好。

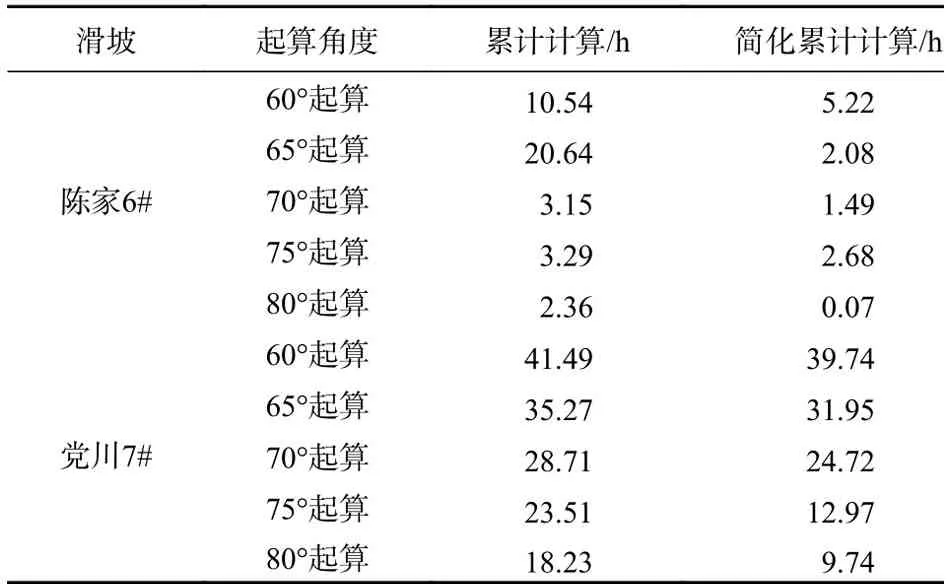
表3 陈家6#和党川7#滑坡预测结果的均方根误差Table 3 RMSE of the predicted results of the Chenjia 6# and Dangchuan 7# landslide

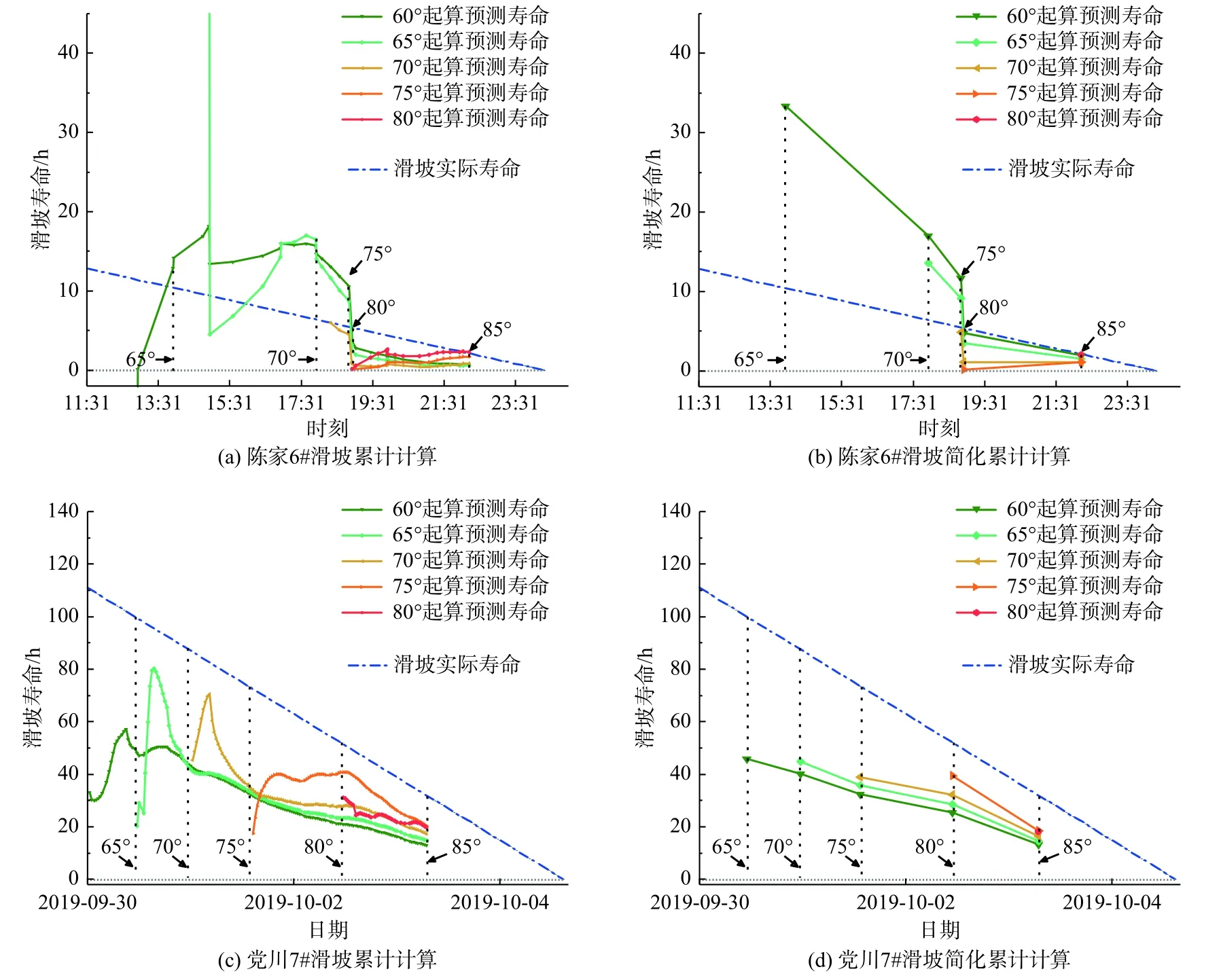
图7 陈家6#和党川7#滑坡预测寿命Fig.7 Predicted life expectancy of Chenjia 6# and Dangchuan 7#

3.2 静态液化型滑坡

静态液化型滑坡整体呈座椅状，凹向台塬内部，底部有大量地下水渗出，后壁陡峭。滑坡的发育一方面是由于该地区黄土颗粒以粉粒为主，黏粒含量较少，拥有易于产生静态液化的颗粒级配；另一方面，该地区多年大水漫灌的灌溉方式导致地下水位不断抬升，由于黄土层底部粉质黏土层的隔水性，塬边黄土层底部易形成饱水层，形成软基效应，这成为静态液化产生的先决条件[31]。滑后弧形凹槽地貌产生的汇水作用和坡脚滑坡体堆积造成的地下水雍高也容易导致该类滑坡呈渐进后退式发育。党川4#滑坡就是一起典型的静态液化型滑坡，滑坡变形曲线如图8所示。滑坡前期变形缓慢且不明显，位移和变形速率没有明显变化，切线角在失稳前18 min才达到85°，突发性极强。

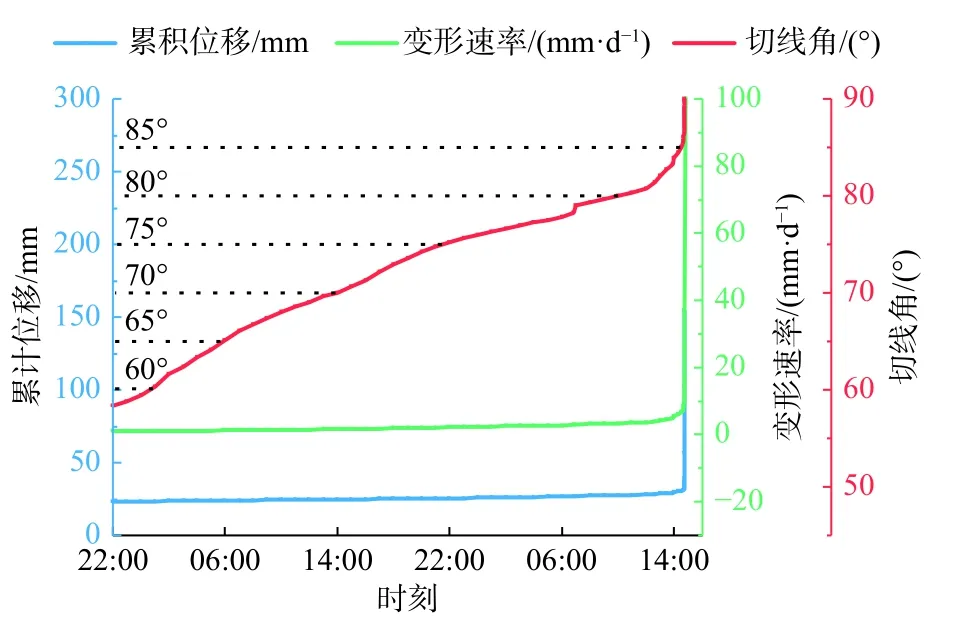
图8 党川4#滑坡变形曲线Fig.8 Deformation curve of the Dangchuan 4# landslide

从党川4#滑坡各变形阶段的预测寿命图（图9）可以看出，两种计算方式得到的各变形阶段预测寿命变化趋势相近，且预测寿命多大于实际滑坡寿命，说明预测失稳时间多晚于实际失稳时间。在切线角达到80°后，预测寿命开始向实际寿命线收敛。

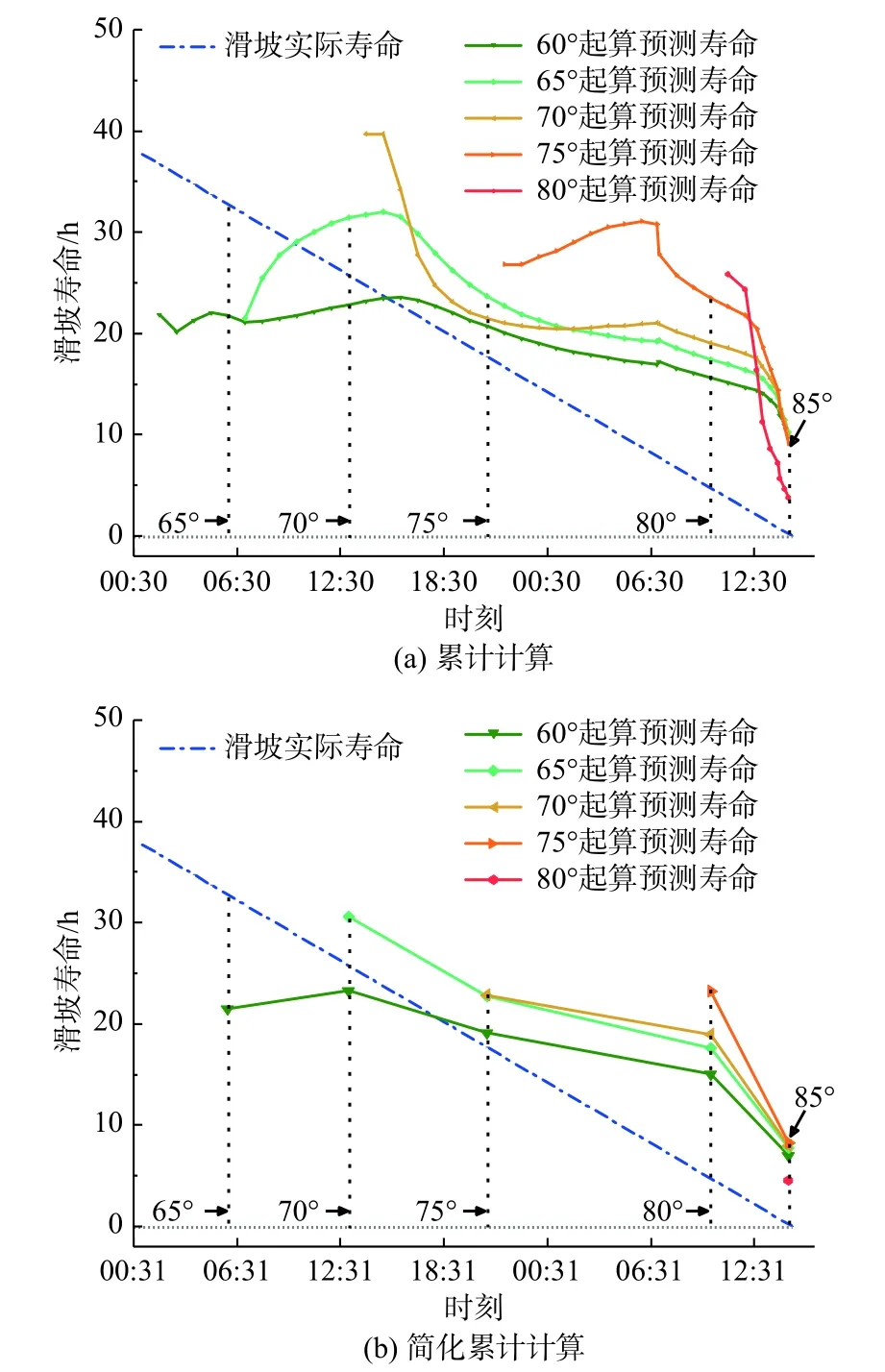
图9 党川4#滑坡预测寿命Fig.9 Predicted life expectancy of the Dangchuan 4# landslide

对比两模型得到的各变形阶段预测结果均方根误差（表4）可以看出，简化累计计算方式的预测精度略高于累计计算方式，但两种计算方式的预测误差均较大。从80°切线角起算得到的预测结果均方根误差较小，在切线角达到80°之后，各变形阶段的预测寿命开始向实际寿命线收敛。总体来看，斜率模型在静态液化型滑坡中的预测效果较差。

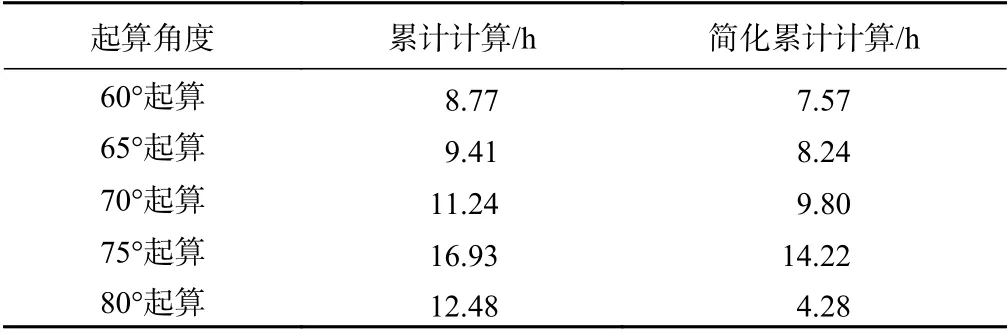
表4 党川4#滑坡预测结果均方根误差Table 4 Predicted RMSE of the Dangchuan 4# landslide

3.3 预测结果分析

3.3.1 速度倒数变化趋势的影响

各变形阶段预测结果提前或滞后预测概率的大小与速度倒数曲线的凹凸性有关。以党川4#和党川7#滑坡为例进行分析，在切线角达到70°之后，党川4#滑坡各变形阶段得到的预测失稳时间多晚于实际失稳时间，而党川7#各变形阶段得到的预测失稳时间均早于实际失稳时间。对比70°切线角之后两滑坡各变形阶段速度倒数曲线图（图10）可以看出，党川4#滑坡速度倒数曲线呈“凸”型，党川7#滑坡速度倒数曲线呈“凹”型，由于斜率模型是速度倒数法在线性条件下的变形，前提假设为滑坡加速阶段的速度倒数变化符合线性趋势，即速度倒数曲线为一条直线，该直线与时间轴的交点即为失稳时间点[9]。对于党川4#这类速度倒数图像呈“凸”型的滑坡，其前期速度倒数变化符合线性趋势，但临滑阶段速度迅速增加，速度倒数迅速向时间轴收敛，偏离了前期线性趋势，前期线性趋势线与时间轴的交点多滞后于实际失稳点，故滞后预测概率大。而对于党川7#这类速度倒数图像呈“凹”型的滑坡，其前期速度倒数的线性趋势与时间轴的交点多早于实际失稳点，故提前预测概率大。

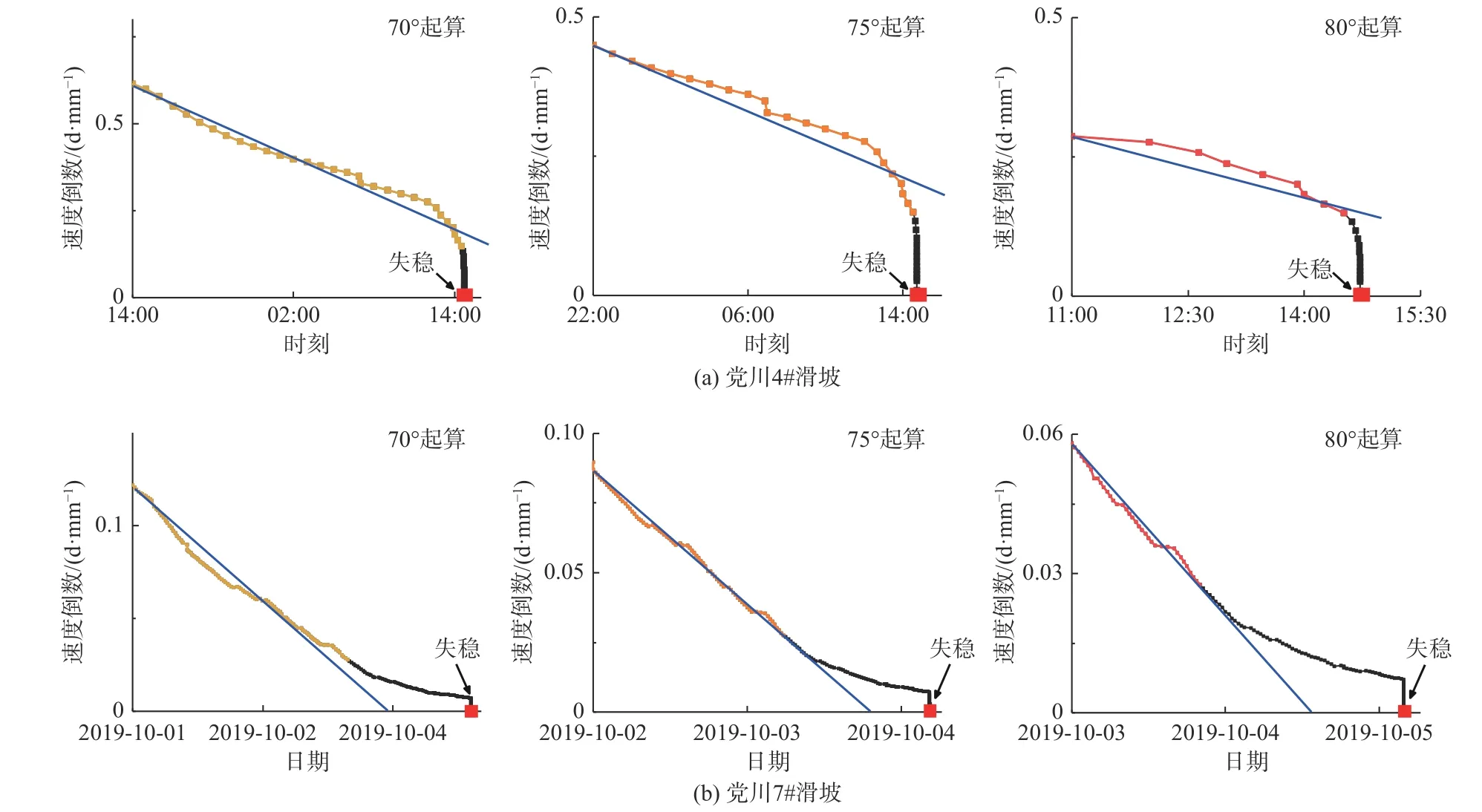
图10 滑坡速度倒数曲线图Fig.10 Inverse velocity of landslides

3.3.2 滑坡成灾模式的影响

滑坡成灾模式不同是造成不同滑坡预测结果差异的根本原因。静态液化型滑坡前期变形缓慢且不明显，主要表现为下伏软基在重力和地下水作用下向临空方向缓慢蠕动，变形量大于1 mm/d，坡体后缘发育有裂缝，宽度大于3 mm，坡脚局部渗水；随着变形不断发展，上覆黄土裂缝向坡体内部发育，形成潜在滑动面，下伏饱和土体结构发生改变，坡脚有大量地下水渗出，且有颗粒物质被带出，存在地下水局部雍高现象；当滑坡进入临滑阶段，由变形产生的孔隙水压力来不及消散，逐渐增大，并形成超孔隙水压力，底部饱和黄土层产生液化，坡体发生整体溃散，移动速度骤升[32−33]。滑坡成灾模式如图11所示。所以，受静态液化的影响，该类滑坡临滑阶段速度骤升，速度倒数图像近乎与时间轴垂直，严重偏离了前期线性变形趋势，导致其预测结果偏差大，模型预测精度偏低。

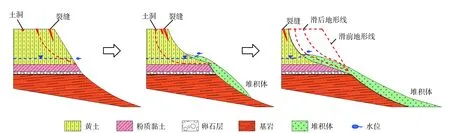
图11 静态液化型滑坡成灾模式图（据文献[27]，有删改）Fig.11 The disaster-causing mode of loess flow landslides（modified from Ref.[27]）

而滑移崩塌型滑坡的变形过程受地下水影响小，滑坡变形主要是坡体在自重作用下向临空面发生移动，上覆黄土体发生不均匀沉降和变形，随着变形的不断发展，裂缝继续向黄土内部扩展延伸，形成潜在滑动面，错台沿平行临空面方向多级发育，其成灾模式如图12所示。受上覆黄土不均匀沉降和裂缝间歇错动的影响，滑移崩塌型滑坡在变形过程中也会出现速度的波动，预测寿命也会随速度变化出现相应的波动。

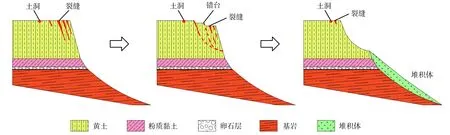
图12 滑移崩塌型滑坡成灾模式图（据文献[27]，有删改）Fig.12 Disaster-causing mode of loess fall landslides（modified from Ref.[27]）

4 讨论

本文以2019年黑方台地区发生的4起突发型黄土滑坡为例，验证了斜率模型在该类滑坡失稳时间预测方面的可行性，但模型预测准确性和适应性还需进行验证总结。对于加速阶段历时极短的黄土滑坡，例如静态液化型滑坡，该模型还是有很大的局限性，仅依靠位移一项监测指标很难实现滑坡失稳临界点的准确预测。有关这类强突发性滑坡的预警预报工作应在考虑滑坡成因机制的基础上，结合位移、倾角、地下水位等多种指标进行综合预警预测。本文提出了以切线角为指标的简化累计计算，降低了数据波动对预测精度的影响，根据滑坡不同变形阶段的变形趋势选择更优的数据处理方法也是今后预警预测工作开展的重点。