国家天文台500米口径球面射电望远镜台址球冠型边坡稳定性分析

陈德茂，沈志平，姜 鹏，付君宜，刘 慧

（1.贵州正业工程技术投资有限公司，贵州 贵阳 550012；2.中国科学院国家天文台，北京 100012）

山区工程建设不可避免地会遇到边坡问题。边坡稳定性评价方法目前主要包括极限平衡法、极限分析法、数值分析法三类。瑞典圆弧法作为极限平衡法的一种最早由Fellenius于1927年提出，Bishop对瑞典圆弧法进行了改进并提出了满足力矩平衡的简化Bishop法[1−2]；针对Bishop法不满足力平衡条件的问题，Janbu提出了满足力平衡条件的Janbu法[3]；郑颖人等[4]分析了几种极限平衡法的精度问题；麻官亮等[5]将Spencer法应用到三维边坡模型的稳定性评价中。极限分析法由Drucker和Prager于1952年提出，该方法考虑了静力场和速度场，根据满足的条件不同分为上限解法（能量法）和下限解法[6−8]，当上限解和下限解相等时即为边坡稳定性的真实解[9]。数值分析法于20世纪60年代提出，目前主要包括有限元法、离散元法、有限差分法、边界元法。基于不同的理论，各数值分析法均有各自的优势和局限性[10−13]。工程中最常用的数值分析方法是有限元法，能够较好地处理小变形问题，配合强度折减法[14−16]可以获得边坡安全系数。

目前极限平衡法依然是工程中常用的边坡稳定性分析方法，该类方法基于平面应变假定而未考虑边坡外形，在评价球冠型边坡这类有明显外形影响的边坡稳定性时有较大误差，本文研究旨在消除该误差问题。

1 FAST台址区域概况

中国科学院国家天文台500米口径球面射电望远镜（Five-hundred-meter Aperture Spherical radio Telescope,FAST）位于贵州省平塘县大窝凼洼地内。大窝凼洼地发育在云贵高原向广西丘陵过渡带的大小井地下河系统中，为“U”字型岩溶洼地，地层岩性由黏土、溶塌混合体、三叠系中统凉水井组石灰岩组成。黏土仅分布于洼地底部，厚度一般3～5 m；溶塌混合体分布于斜坡地带及洼地底部黏土层之下，厚度一般5～50 m，平均30 m；浅表为未胶结的大块石，中下部为半胶结、胶结的土石混合体，均匀性差；三叠系中统凉水井组白云质灰岩、含泥灰岩出露于洼地上部陡坡地段，中至厚层状，属较软至较硬岩，岩体较破碎至较完整。

为契合FAST主动反射面形状，台址开挖完成后在反射面圈梁以下范围内形成了大规模球冠型边坡[17]，如图1所示。由于浅表层未胶结的溶塌混合体极易发生破坏[18]，开挖时清除了大量该类土体，开挖完成后的球冠型边坡主要由胶结的溶塌混合体和下伏基岩组成，局部稳定性良好，但球冠型边坡整体稳定性评价缺少相关计算方法。

图1 FAST台址球冠型边坡Fig.1 Spherical cap shape slope of FAST

考察边坡在水平面内的形状，可将其分为凸形、凹形和直线形，边坡的空间形状对其稳定性无疑会产生影响[19−21]，球冠型边坡属于轴对称圆形凹坡，实际工程中通常不考虑边坡外形，均按照直线形边坡考虑，所得计算结果偏于保守[22−23]，需重新确定其稳定性评价方法。

目前一般认为轴对称圆形凹形边坡稳定性优于直线形边坡，原因是轴对称圆形凹坡的微单元扇形滑体侧面较直线形边坡多了一组侧面力，Zhang[24]和Zhang等[25]都将该侧面力按主动土压力取值，从概念上分析轴对称圆形凹坡的微单元扇形滑体在滑动时侧面处于挤压状态，更接近于被动土压力。黎莉等[26]对侧面力分别按照主动土压力、静止土压力、被动土压力三种情况进行分析，结果表明侧面实际压力状态处于静止土压力和被动土压力之间。

2 轴对称圆形凹坡的微单元扇形滑体侧面力

2.1 环形条块轴向力与外荷载的关系

根据极限平衡法划分条块的思路，将轴对称圆形凹坡滑体划分为若干个“环形条块”（图2），环形条块向下滑动时会受到一个水平分力均布荷载qx，荷载方向指向对称轴（图3）。

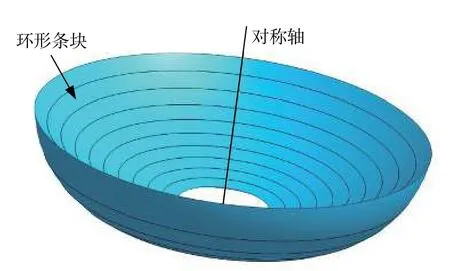
图2 轴对称圆形凹坡划分环形条块Fig.2 Dividing annulus slices of the axisymmetric circular concave slope

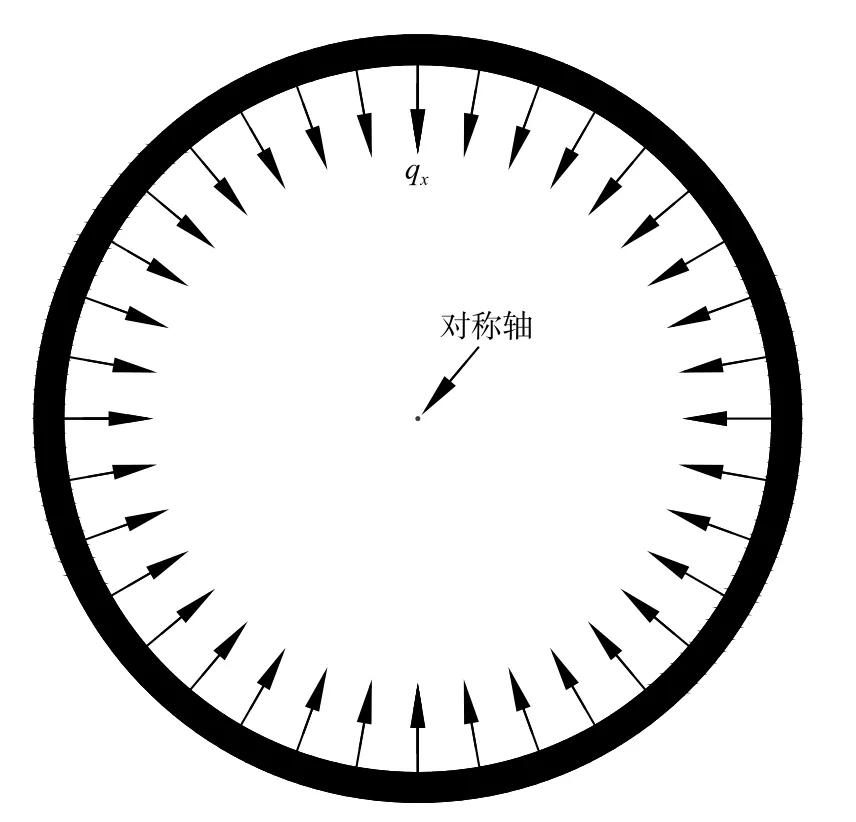
图3 环形条块水平下滑分力Fig.3 Horizontal sliding component of annulus slices

取图3中环形条块的一段微单元扇形滑体作为分析对象（图4）。微单元扇形滑体的曲率半径为环形条块的半径R，两侧面夹角为dφ，用r和s分别表示微单元扇形滑体的法线和切线方向，则微单元扇形滑体弧长ds=Rdφ。s和r方向的荷载集度分别为qs和qr。侧面弯矩为M，侧面剪力为FQ，侧面轴向力为FN。

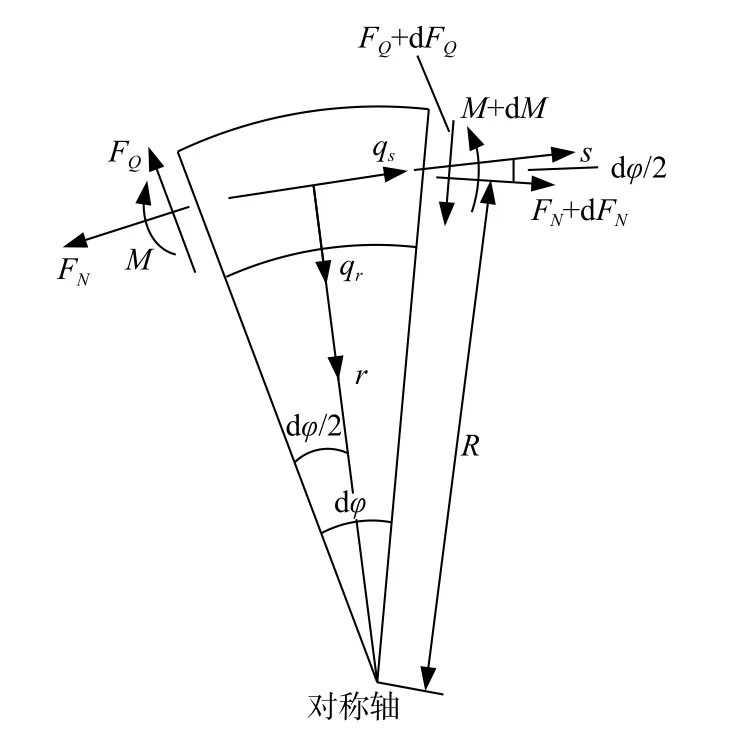
图4 微单元扇形滑体受力图Fig.4 Free-body diagram of the tiny element sector sliding body

由ΣFs=0得

由于dφ趋向于0，则cos（dφ/2）=1，sin（dφ/2）=dφ/2，忽略高阶微量后由式（1）得

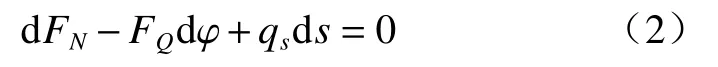
令ds=Rdφ，由式（2）整理得

由ΣFr=0同理可得

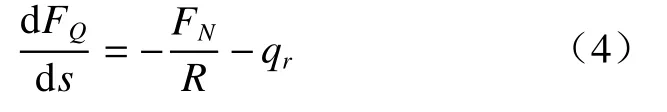
由ΣM=0得

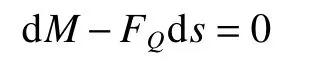
即

由式（3）（4）（5）可知，当R趋向于无穷时，环形条块内力公式转变为直线形条块。

由于环形条块滑动时受到的水平分力qx为均布荷载，故切线荷载qs=0，法向荷载qr=qx。

设环形条块处于无弯矩状态，即侧面弯矩M=0，侧面剪力FQ=0，由式（4）可得

2.2 微单元扇形滑体侧面力与水平抗滑力的关系

由式（6）可知，当环形条块向下滑动时会在环形条块内产生一个轴向压力FN，FN即为微单元扇形滑体的侧面力，且FN为常数。如果可以确定环形条块轴向抗压能力FNmax，则可以得到一个水平荷载，该水平荷载方向背离对称轴，起到抗滑作用，属于抗滑力。

如图4所示，假定极限平衡状态时，微单元扇形滑体的大主应力σ1方向为s切线方向，小主应力σ3方向为重力方向（竖直方向），则有：

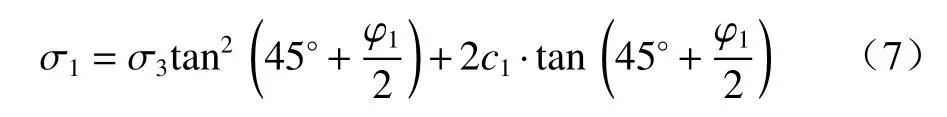
考虑到边坡坡面临空，假设小主应力σ3=0，则有：

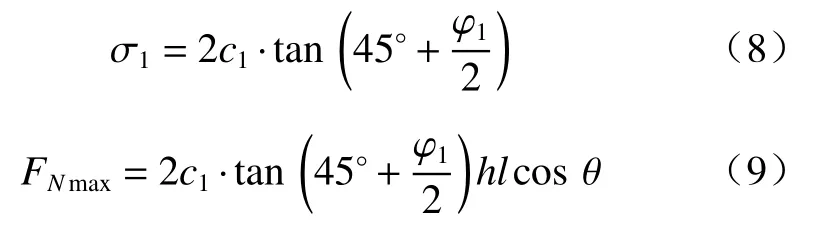
式中：h—微单元扇形滑体的高度；

l—微单元扇形滑体的底面宽度；

θ—微单元扇形滑体的底面与水平面夹角；

c1—微单元扇形滑体的滑体黏聚力；

φ1—微单元扇形滑体的滑体内摩擦角。

对于一般土体，式（8）中的σ1介于静止土压力和被动土压力之间，符合文献[26]的结论。

取微单元扇形滑体（图5），由式（6）可得FNmax产生的水平抗滑力（T）的计算公式：

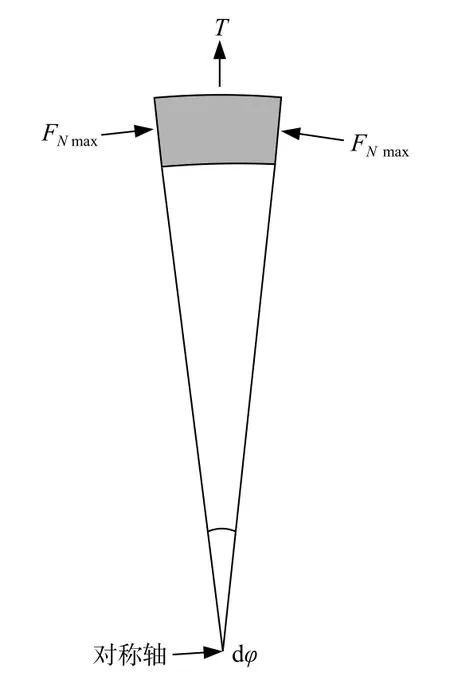
图5 微单元扇形滑体抗滑力分析Fig.5 Sliding resistance force of the tiny element sector sliding body

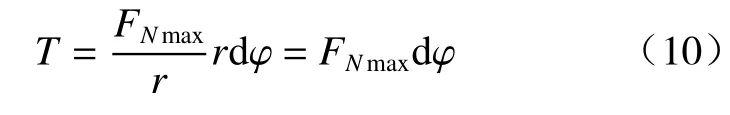
计算大主应力σ1时由于假定σ3=0，对于坡面处的滑体部分较为合理，但对于深处的滑体部分其σ3不为0，故式（10）计算出的水平抗滑力偏小，使得最终稳定性评价结果偏于保守。

3 基于极限平衡法的轴对称圆形凹坡稳定性评方法

3.1 改进简化Bishop法

将2.2节中介绍的水平抗滑力加入到任意极限平衡法中，均可以使其适用于轴对称圆形凹坡稳定性评价，这里以简化Bishop法为例进行公式推导。

取第i个环形条块的微单元扇形滑体i，将水平抗滑力Ti引入到简化Bishop法中，假定水平抗滑力Ti作用在微单元扇形滑体i的重心上，微单元扇形滑体i重心所在剖面的计算简图如图6所示。

图6 改进简化Bishop法计算简图Fig.6 Calculation diagram of the improved simplified Bishop method

由竖向合力ΣFz=0得

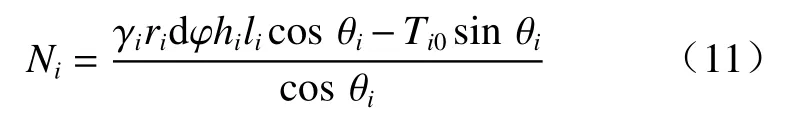
式中：γi—微单元扇形滑体i的土体容重；

Ti0、Ni—微单元扇形滑体i在滑面上的抗滑力和法向力；

ri—微单元扇形体重心到对称轴的距离；

其余变量意义同前。

由力矩求和ΣMO=0得：

式中：Ri—微单元扇形滑体i的水平抗滑力Ti到圆弧滑面圆心O的力矩；

R—圆弧滑面半径。

由摩尔库伦强度准则并引入安全系数Fs可得Ti0：

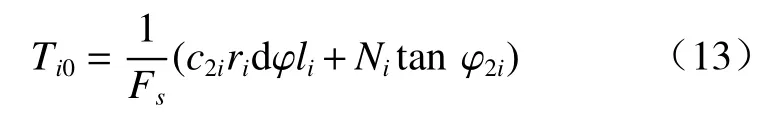
式中：c2i—微单元扇形滑体i的滑面黏聚力；

φ2i—微单元扇形滑体i的滑面内摩擦角；

其余变量意义同前。

将式（11）代入式（13）整理得：

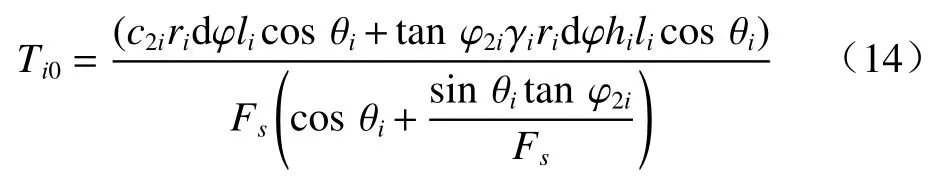
将式（14）代入式（12），约去dφ整理得：

3.2 改进简化Bishop法验证

3.2.1 简化Bishop法和强度折减法对比

首先对有限元强度折减法和简化Bishop法在计算直线形边坡时安全系数的差异进行对比：简化Bishop法采用Geostudio，自动搜索滑移面；有限元强度折减法采用Midas GTS NX。为控制有限元模型中滑移面为圆弧形，模型分为基岩和土体两部分，边坡高10 m，坡度42.5°，土体参数如表1所示，所有土体均采用摩尔库伦强度准则，安全系数及滑移面计算结果如图7所示。

表1 10 m高度边坡土体参数Table 1 Soil parameters of slope with a height of 10 m

图7 简化Bishop法与强度折减法安全系数计算结果Fig.7 Safety factor of the simplified Bishop method and strength reduction method

由图7可以看出两种方法的滑移面基本一致，但有限元强度折减法的安全系数计算结果略高于简化Bishop法[27]，这主要是因为简化Bishop法有诸多假定，如未考虑土条间切向力、未考虑单个土条的力矩平衡等，这些假定使得计算结果偏于保守。

3.2.2 改进简化Bishop法和强度折减法对比

建立图7（b）模型的三维有限元模型（图8），坡脚到对称轴的距离Rbottom分别为5，10，20 m。计算得到安全系数和滑移面后，将滑移面提取并采用式（15）—（17）进行安全系数计算，并将有限元强度折减法计算结果和式（15）—（17）的计算结果进行对比，结果见图9（a）。图中H为边坡高度，H/Rbottom=0表示直线形边坡；同时将表1土体参数的黏聚力改为10 kPa，其余参数不变，进行安全系数计算对比，计算对比结果如图9（b）所示。

图8 三维有限元模型（Rbottom=20 m）Fig.8 Three-dimensional finite element model（Rbottom=20 m）

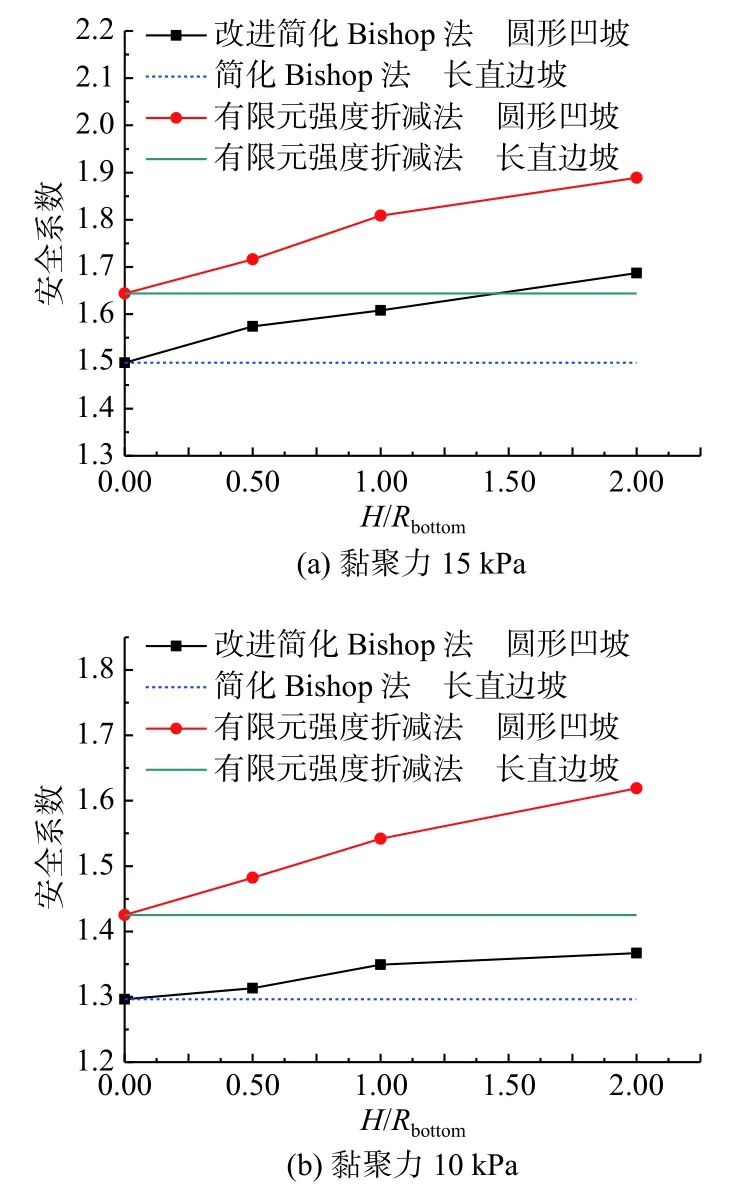
图9 10 m高轴对称圆形凹坡安全系数计算结果Fig.9 Safety factor of the axisymmetric circular concave slope with a height of 10 m

另建立两组模型进行对比验证，边坡模型高度为30 m，边坡坡度60°，土体参数如表2所示，安全系数计算结果如图10（a）所示。同时将表2土体参数的黏聚力改为35 kPa其余参数不变，进行安全系数计算，计算结果如图10（b）所示。

表2 30 m高度边坡土体参数Table 2 Soil parameters of slope with a height of 30 m

由图9和图10可得，有限元强度折减法安全系数计算结果始终高于改进简化Bishop法且两条计算结果线段接近平行，表明两种计算方法的安全系数差值基本保持一致，改进简化Bishop法的计算公式较为可靠，同时可以看出轴对称圆形凹坡的稳定性优于直线形边坡。

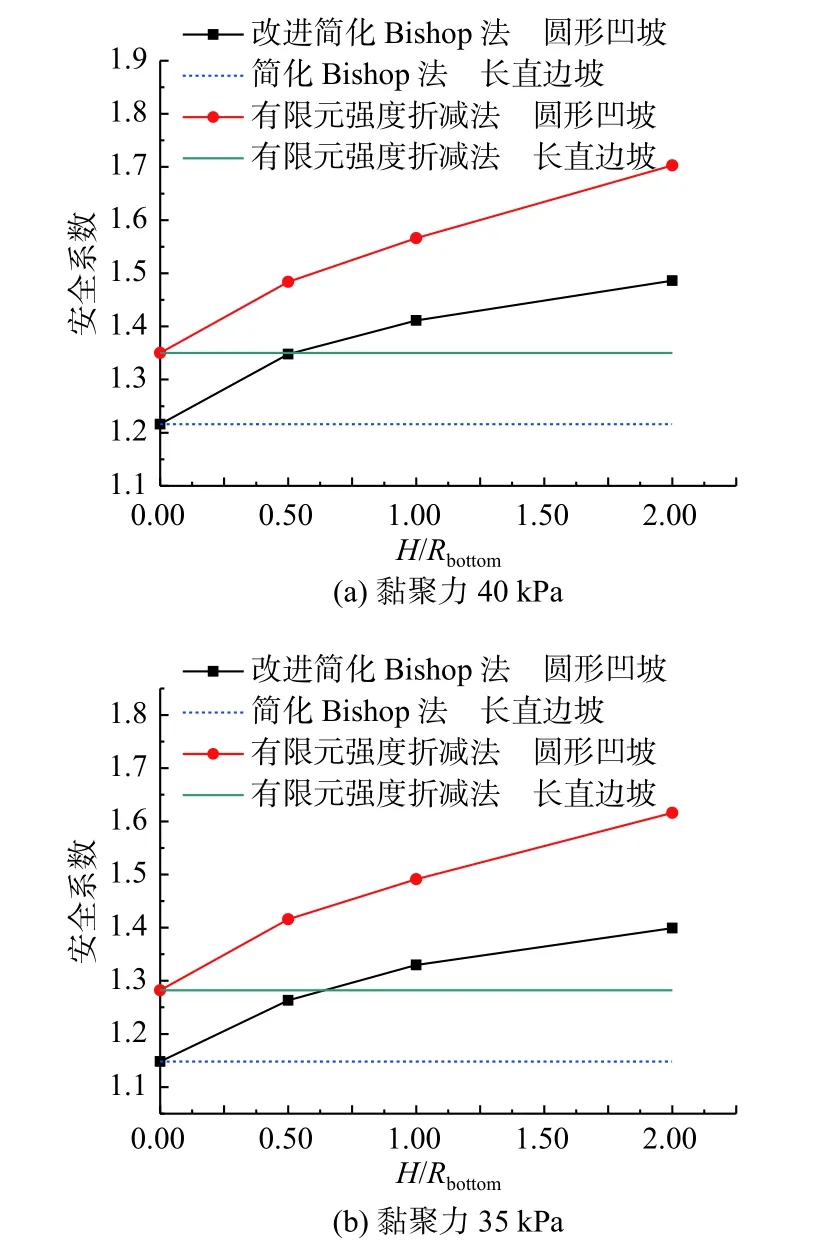
图10 30 m高轴对称圆形凹坡安全系数计算结果Fig.10 Safety factor of the axisymmetric circular concave slope with a height of 30 m

4 轴对称圆形凸坡的稳定性评价

轴对称圆形凸坡的安全系数计算公式可由式（15）—（17）变换得到，当轴对称圆形凸坡的环形条块下滑时其轴向会产生一个拉力，一般不考虑土体的抗拉强度，则忽略式（17）得到适用于轴对称圆形凸坡的安全系数计算公式：

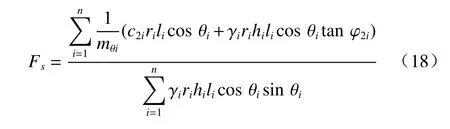
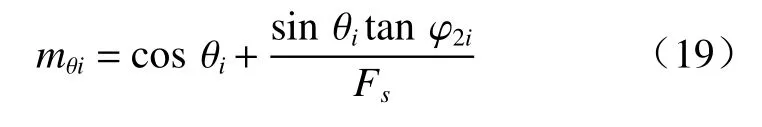
对式（18）（19）进行验证，同样采用有限元强度折减法和改进简化Bishop法计算得到的安全系数结果进行对比。建立有限元模型，土体单元采用表2中的土体参数，边坡高度20 m，坡度为70°，Rbottom=20，30，40 m三种情况（图11），两种方法计算结果如图12所示。

图11 轴对称圆形凸坡三维有限元模型Fig.11 Three-dimensional finite element model of the axis ymmetric circular convex slope

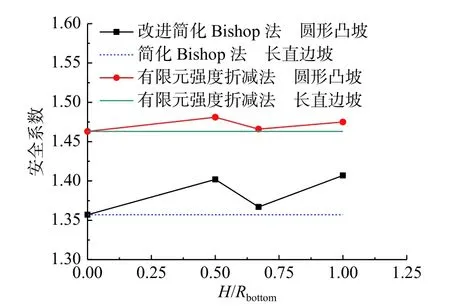
图12 轴对称圆形凸坡安全系数计算结果Fig.12 Safety factor of the axisymmetric circular convex slope

图12中两种方法安全系数计算结果比较接近，式（18）（19）适用于轴对称圆形凸坡安全系数计算，同时轴对称圆形凸坡的安全系数随半径的增大没有发生明显变化，与传统概念中凸坡的稳定性差有所出入。这主要是因为上部环形条块周长要小于下部环形条块，即上部滑体的体积较小而下部滑体的体积大，这种情况对抗滑移是有利的，凸坡安全系数未必就比直线形边坡小[22]。

5 结论

（1）轴对称圆形凹坡侧面力取值可以按照微单元扇形滑体小主应力为零时的大主应力进行取值。

（2）考虑侧面力取值后对极限平衡法进行改进，提出改进后的简化Bishop法安全系数计算公式，改进后的公式计算结果与数值分析结果基本一致。

（3）假定土体抗拉强度为零，提出了圆形凸坡安全系数计算方法与公式，计算结果表明圆形凸坡安全系数与长直边坡接近。