高岭土电渗固结特性及数值模拟研究
2021-07-23沈美兰周太全李吴刚
沈美兰,周太全,李吴刚
(江南大学环境与土木工程学院,江苏 无锡 214122)
沉积软土具有含水率高、压缩性高、渗透系数低、强度低等特点,采用传统的堆载预压法、真空预压法排水时间过长,施工期间可能引起土体剪切强度破坏。电渗法使得软土内部形成较大孔隙水渗流,从而可以加快软土排水,是固结软土的有效方法。Casagrande[1]将电渗技术首次运用到铁路工程中。Lamont-Black[2]对较大范围的路基边坡土进行电渗处理,排出水量7300 L。为探究电渗排水固结机理,众多学者进行了室内试验研究。胡黎明等[3]探究不同干密度下土体的排水效果分析,发现随着土体干密度的增大,排水量和排水速率逐渐减小。Hamira等[4]对高岭土进行电渗排水试验,发现25 V电压下高岭土的排水量为10 V电压下的1.55倍,但单位体积排水量耗能更高。李瑛[5]对杭州土的电渗排水试验表明低电压条件下的电渗渗透系数较高。金志伟等[6]研究表明,真空-电渗联合排水法可以对低含水率盾构泥浆进行脱水分离。
随着电渗技术在岩土工程中的应用,电渗固结理论也得到进一步的发展。为预测土体电渗固结特性,Esrig[7]首先提出了一维电渗固结理论和解析解。徐伟[8]基于太沙基固结理论和电渗固结理论,进行了堆载预压-电渗联合工况下的室内试验和数值分析。胡黎明[9]在Biot固结理论的基础上,进行电场、渗流场和应力场等多场耦合模型数值分析,发现试验结果与数值分析结果吻合良好。龚明星[10]考虑有效电势变化情况下求出平均固结度和孔隙水压力的解析解。Wu等[11]采用真空预压联合电渗工况下的轴对称模型,考虑水平和竖向渗流,推导出任一点的超静孔压理论解。本文基于室内电渗试验研究电势梯度对高岭土固结的影响,进行不同电势梯度条件下高岭土电渗固结试验,研究电流、排水量、沉降量和有效电压随时间的变化,测量电渗后土体的含水率分布,并对最终的单位排水能耗进行分析。基于多物理场仿真分析软件Comsol Multiphysics实现电渗固结有限元分析,通过室内试验与数值分析对比,研究不同电势梯度条件下电渗固化高岭土固结性状,为电渗试验和工程应用提供技术依据。
1 室内模型试验
1.1 试验装置
试验装置如图1所示,其中图1(a)为整体电渗试验系统,包括电渗试验槽、电路和测量系统,电渗试验槽为自制的有机玻璃电渗槽(图1b),包括阳极腔室、矩形盛土器、阴极腔室。电渗装置整体外形尺寸为370 mm×146 mm×200 mm,底板厚度为10 mm,其余板厚均为5 mm。电渗槽左右两侧底部分别设有排水孔,以排出电渗过程中的水。距离电渗装置左右侧板4 cm处分别设置1块多孔透水板,距多孔排水板0.5 cm处,每隔6 cm设置1个电势测孔,采用钛合金探究电渗过程中土样内部的电势分布。为防止电极腐蚀的影响,电极材料为镀钌钛网。在电渗装置中部和左右两侧分别安装位移传感器,监测试验过程土样的竖向变形。

图1 电渗试验装置图Fig.1 Diagram of the electro-osmotic test
1.2 试验方法
(1)土样的配制
本试验采用商品高岭土,含水率49%,比重2.72,液限15%,塑限49%,塑性指数 34。
将高岭土放入烘箱,在温度105 °C条件下烘24 h,除去水分,取出在室温下冷却。随后将高岭土配制成目标含水率49%的土料,搅拌完后对土料抽真空以去除气泡。静置24 h,使水分分布均匀。
电渗槽内侧壁涂抹凡士林,以减小边界效应对土样固结的影响。将土料分层装入模型箱中,每层土料高度为5 cm,并对土料振捣以排出装料过程中混入的气泡;装料结束后在上部覆盖保鲜膜,减小试验过程中表层土料水分蒸发对试验结果的影响。
(2)试验方案
进行3组电渗试验,电势梯度分别为0.5,1.0,1.5 V/cm(分别对应13,26,39 V的电压),电渗时长为48 h,每隔1 h监测电流、排水量和沉降量。电渗结束后分别测量土体阳极、中部和阴极位置处上、中、下三层的含水率。
2 试验结果与分析
2.1 土体电流和排水量
土体中电流和排水量随时间的变化关系如图2所示。试验结果表明:电势梯度越大,土样中电流越大且衰减速度越快,在电渗至24 h左右,土样中的电流趋于稳定。0.5,1.0,1.5 V/cm电势梯度条件下的最终平稳电流分别为20,30,40 mA左右。同时,电势梯度越大,土样的前期排水速度越快,之后逐渐减小,直到20 h左右趋于平稳,表明20 h后土体固结程度接近完成。土样的最终排水量分别为100,320,400 mL,与电势梯度呈正相关。1.5 V/cm电势梯度条件下,土体最终排水量较0.5,1.0 V/cm电势梯度条件下分别增加263.3%、21.3%左右。
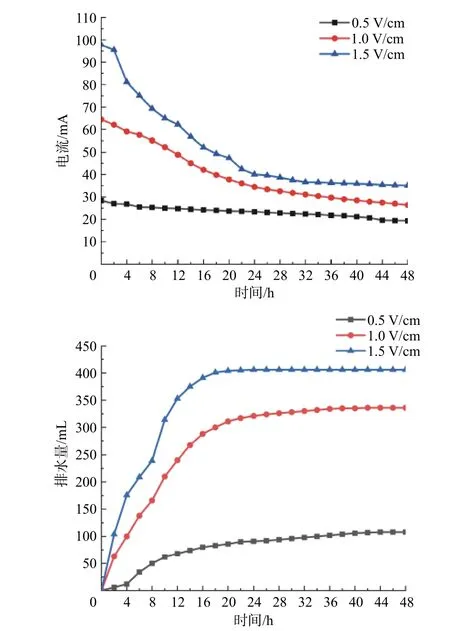
图2 土体中电流和排水量与时间关系曲线Fig.2 Changes of the current and drainage with time of the soil
3组高岭土试样初始孔隙比、含水量相同,电势梯度越大,电渗流速度越大,排水总量也越大;电渗流速度和土体电流正相关[12],所以电势梯度越大,土体中的电流也越大。
2.2 土体沉降和含水率
3种电势梯度下沉降随时间的变化关系如图3所示。在电势梯度0.5,1.0,1.5 V/cm条件下,阳极处的土体沉降量分别为4.5,9.5,9.8 mm,土样中部的沉降量分别为6.2,10.2,10.6 mm,阴极处的最终沉降量分别为3.9,5.9,6.0 mm。图4为最终各位置处含水率分布曲线,呈现阳极处含水率小于阴极处含水率、高电势梯度土体含水率低于低电势梯度土体含水率的现象。由二维电渗固结理论可知[13]:负超静孔隙水压力从阳极到阴极呈线性减小,阴极处负超静孔隙水压力基本为0,导致土体竖向沉降量从阳极到阴极逐渐减小,阳极土体靠近电渗槽边缘,受侧摩阻力的影响,限制了阳极土体的沉降,所以最终中间位置处沉降量最大。
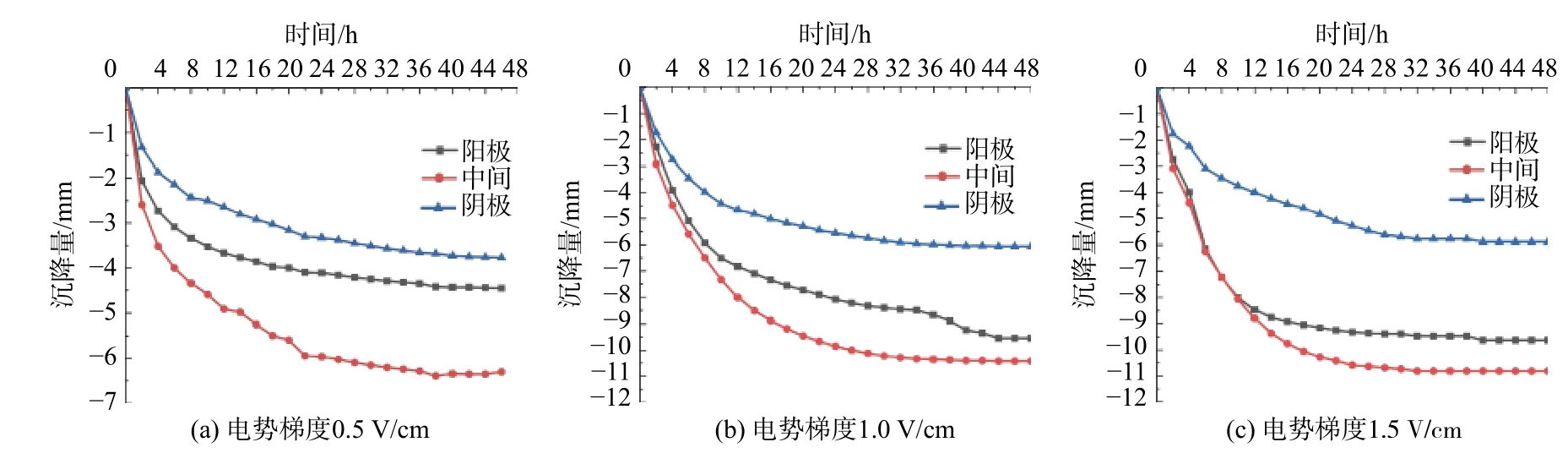
图3 土体沉降量-时间关系曲线Fig.3 Changes of soil settlement with time
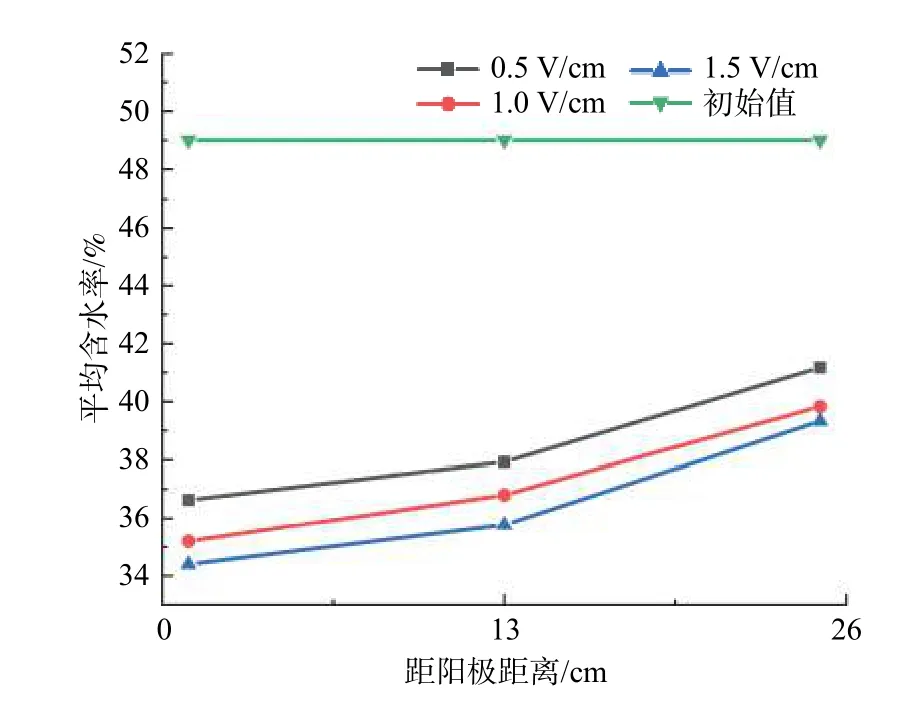
图4 土体最终含水率分布Fig.4 Final water moisture distribution of soil
2.3 土体两端有效电压
从阳极到阴极等间距分布5个电势测点,编号为1~5,电势随时间变化曲线如图5所示。假定平行于土体横截面每1 cm厚的单位土层电阻值保持不变[14],两端电势测点距阴阳极都为1 cm,占盛土器总长度的4%左右。可近似认为电势测点1和5之间的电势差为土体两端有效电压。
由图5也可以得出,两端有效电压随时间变化拟合得到的指数曲线基本趋势一致。最终电势梯度越大,有效电压随时间降低速度越大;随着电势梯度减小,有效电压降低趋势减小。有效电压前期降低较快,后期降低较慢。
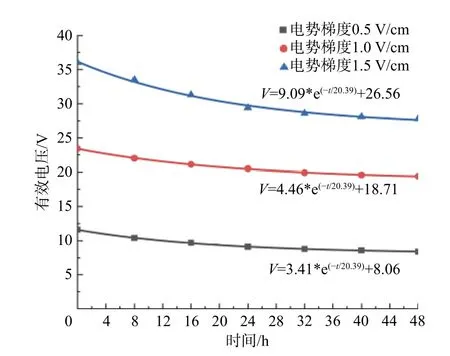
图5 两端有效电压-时间关系曲线Fig.5 Changes of the effective voltage at both ends with time
20 h之前土体排水量较大,负孔隙水压力逐渐发展,土体发生体缩,电极板与土体脱离,且电势梯度越大排水速率越快,阳极处含水率降低加快,而阴极处含水率变化幅度较小,所以土体与阳极接触电阻增大;且电势梯度越大,裂隙发育程度越高,如图6所示。土体电阻变大,电压降速率越快,20 h后排水量趋于稳定,有效电压也逐渐趋于平稳。

图6 电渗实物图Fig.6 Physical picture of the electro-osmosis
2.4 能耗分析
单位排水能耗的表达式为[14−15]:
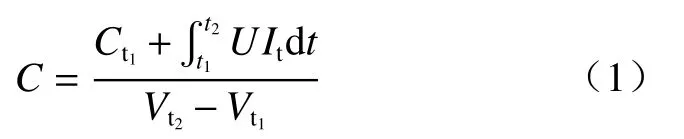
式中:U—电源的输出电压/V;
It—t1、t2时间段内某时刻的输出电流/A;
Ct1、Ct2—t1、t2时刻的能耗值;
Vt1、Vt2—t1、t2时刻的排水量。
由图2可以看出,3种电势梯度条件下,前20 h土体排水量较大,电流曲线和排水量曲线在前20 h区分较为明显,因此,选取0~20 h区段排水量和电流数据进行单位排水能耗分析。单位能耗随时间的变化曲线如图7所示,3种电势梯度下,单位时间排水能耗在前0~8 h呈现快速增长趋势,8~10 h呈现递减趋势,后期随时间增长能耗逐渐增大,但增长趋势减缓。

图7 单位排水能耗-时间变化曲线Fig.7 Changes of energy consumption of per unit drainage with time
1.5 V/cm电势梯度试验条件下单位排水能耗最大,主要是因为在该试验条件下土体含水率下降程度最大,局部电阻增大产生较大焦耳热且电渗土体出现较大的裂隙,排水通道下移,改变了渗流路径(图6),电极板与土体脱离导致接触电阻增大。电势梯度1.0 V/cm试验条件下,土体裂缝发育程度较低,对土体排水通道影响较小,最终单位排水能耗在相同时间内略大于电势梯度0.5 V/cm的能耗,所以在电渗固结过程中电势梯度并非越大越好,综合3种电势梯度下排水量和单位排水能耗分析,本文的经济电势梯度为1.0 V/cm。
3 高岭土电渗固结数值模拟
3.1 电渗固结方程及数值解
土体电渗固结控制方程组包括:基于有效应力的平衡微分方程、孔隙水流动连续方程、电荷守恒方程[16−17]。由Biot固结理论和有效应力原理可以得到平面应变条件下的平衡方程:

土中孔隙水流动会引起土体体积变化,土体处于饱和状态,并且土体颗粒不可压缩,可以得到土体孔隙水流动连续方程[9]:
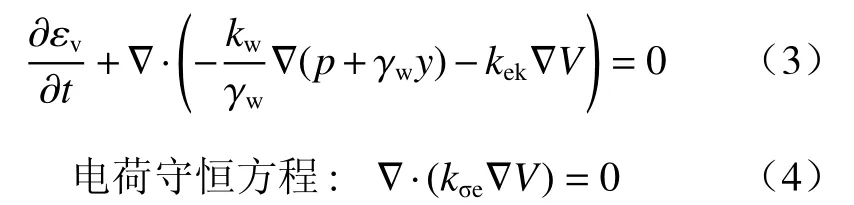
γw—水的重度;
p—孔隙水压力;
εv—土体骨架体积应变;
V—电势。
边界条件:第一类为Dirichlet条件:位移边界条件,给定边界孔隙水压力大小;第二类为Neumann边界条件:应力边界条件,孔隙水压力边界流量。
渗透系数kw、电渗透系数kek是孔隙比e的函数,可以表示为[17]:
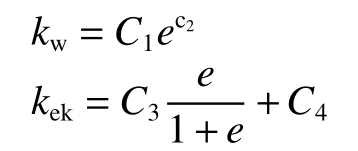
电导率kσe是孔隙比e的函数,可以表示为[18]:

参数C1、C2、C3、C4为拟合参数,可采用试验进行拟合;如缺少试验拟合数据,可参考文献[19]取用。
采用Galerkin方法对电渗固结控制方程组进行离散,利用Comsol Multiphysics多物理场仿真软件实现上述电渗固结有限元分析。
3.2 一维电渗固结分析验证
为了验证电渗固结分析程序的有效性,对具有解析解的Esrig一维电渗固结问题进行数值分析。计算模型为:阴极位于土柱上部,排水面;阳极位于土柱下部,不排水;阳极电势13 V,阴极电势为0 V。
计算参数:L=1 m,mv=1.0×106Pa−1,E=7.4×105Pa,kw、kek、kσe均为常量,其中kw=2.0×10−8m/s,kew=2.0×10−9m2/Vs。
Esrig提出一维固结理论模型:
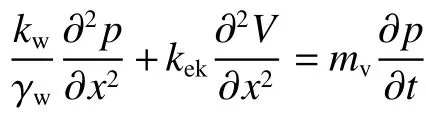
阴极排水、阳极不排水情况下,Esrig一维固结理论具有解析解[16]。
超静孔隙水压力Esrig解析解[16]和数值解对比如图8所示,表明编写的电渗固结数值分析程序是可靠的。
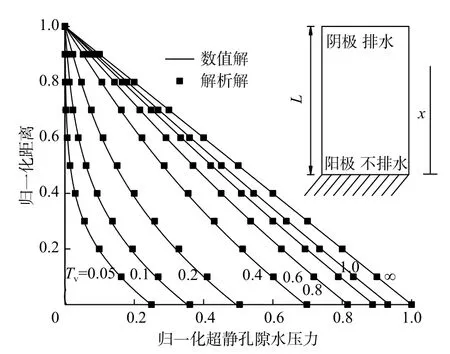
图8 一维电渗固结超静孔隙水压力时空分布Fig.8 Dimensionless excess pore water pressure as a function of dimensionless time and distance for 1D electroosmosis
3.3 高岭土电渗固结试验数值模拟
按照图1(b)实验建立有限元模型,采用四节点单元离散,对高岭土电渗固结进行数值分析。阳极电势设置为13,26,39 V,对应电势梯度0.5,1.0,1.5 V/cm,阳极和底部设置为不排水边界,阴极和表面为排水边界;两侧设置侧向弹性约束以反映箱壁对土体摩擦力影响,底部设置竖向约束。对3种电势梯度电渗固结试验进行了数值模拟分析,得到模型表面和阳极沉降量、阳极超静孔隙水压力分布、阳极表面固结度。
从图9(a)可以看出,表面沉降量最大值发生在距离阳极5 mm位置处,模型表面沉降量呈现出阳极大、阴极小的“勺子”形状,这和胡黎明[18]、吴辉[20]的试验观测结果一致;阳极沉降量计算值与试验值的对比分析结果表明,3种电势梯度电渗固结沉降量计算值发展趋势和试验结果吻合良好,说明电渗固结数值模拟结果合理,如图9(b)所示。

图9 模型表面及阳极固结沉降Fig.9 Consolidation settlement at the model surface and anode
由图9(c)可知,随着电势梯度的增加,阳极土体沉降量逐渐增大; 电势梯度由0.5 V/cm增加到1.0 V/cm时,阳极沉降量由4.45 mm增加到8.54 mm,增加幅度为92%,而当电势梯度由1.0 V/cm增加到1.5 V/cm时,阳极沉降量由8.54 mm增加到9.63 mm,增加幅度为13%;沉降量和电势梯度呈非线性关系,表明采用非线性模型进行电渗固结计算是必要的。
由图10(a)可知,阳极超静孔隙水压力都是负孔压,自上往下呈曲线分布,最大值出现在阳极底部;随着电势梯度的增加,阳极底部负孔压呈非线性增长趋势;当电势梯度由0.5 V/cm增加到1.0 V/cm时,土体最大负超静孔隙水压力增长幅度为93%;当电势梯度由1.0 V/cm增加到1.5 V/cm时,土体最大负超静孔隙水压力增长幅度仅为8.8%。可见电渗固结试验时,电势梯度并非越大越好,应选择合适的电势梯度。
由图10(b)可看出,在3种电势梯度作用下,归一化阳极超静孔隙水压力时空发展关系一致。在电渗固结过程中,阳极位置超静孔隙水压力都为负孔压,随时间推移负孔压逐渐增长,土体内部水分逐渐排出,固结度逐渐增加。由图10(c)可知,在3种电势梯度作用下,阳极位置土体平均固结度发展一致,在20 h时1.5,1.0,0.5 V/cm电势梯度条件下,土体固结度试验结果分别为90%、90%、95%,计算结果为100%,表明20 h土体固结接近完成。电渗过程中,归一化土体超静孔隙水压力时空发展情况一致,土体平均固结程度基本一致。
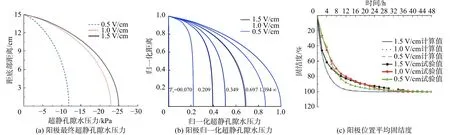
图10 阳极超静孔隙水压力及固结度Fig.10 Anode excess pore pressure distribution and consolidation degree
4 结论
(1)3种电势梯度条件下,土体电流呈现分阶段衰减趋势。前20 h电流衰减速率较大,后28 h电流衰减趋于平缓。土体电渗排水量、沉降量均表现出先随时间增大、后趋于平缓的规律。
(2)土体两端有效电压呈现先沿着指数曲线下降、后逐渐趋于平稳的趋势。单位排水能耗呈现的规律为:C1.5 V/cm>C1 V/cm>C0.5 V/cm,本次试验的经济电势梯度为1.0 V/cm。
(3)基于Comsol Multiphysics多物理场仿真软件实现了电渗固结试验有限元模拟,一维电渗固结理论解与数值解吻合良好。
(4)数值模拟表明,3种电势梯度条件下,归一化阳极超静孔隙水压力时空变化过程一致;电势梯度由0.5 V/cm增加到1.0 V/cm较电势梯度由1.0 V/cm增加到1.5 V/cm时的最大超静负孔压增长幅度大,说明电势梯度并非越大越好,在实际工程中可以选择合适的电势梯度进行电渗试验。
