LTL 性质的可监视性

2021-07-23王伟芳樊丽丽李宝凤赵光峰

唐山师范学院学报 2021年3期

王伟芳，樊丽丽，李宝凤，赵光峰

（唐山师范学院数学与计算科学学院，河北唐山 063000）

可监视性质的形式定义由Pnuel 和Zaks 首次提出[1]，是指通过对系统动作的观察，就可以判断它的任何继续是否属于一个形式化准述的语言。在过去几年里，一些作者也研究了正则语言的可监视性并给出了几种构造监视器的方法，还有一些学者用LTL3来研究LTL的可监视性[2-5]。本文从LTL的语义和可监视的定义出发，证明LTL性质的可监视性。

1 符号说明

∑ω的子集称为性质（语言）。如果L是无限单词的语言，则Lc表示它的补集，即Lc=∑ωL。

2 预备知识

由拓扑学知识，很容易给出∑ω上的一个拓扑基如下：

可以证明这个子集族生成拓扑

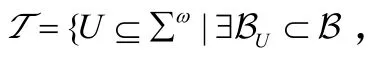
在这个拓扑空间，L是安全性质[7-9]当且仅当L是闭集，L是余安全性质当且仅当L是开集。

定义1令L是拓扑空间∑ω的子集。

——若集合L是闭集，则称L是安全集；

——若集合L是开集，则称L是余安全集。

定义2令L是拓扑空间∑ω的子集。若∀x∈∑ω，∀p＜x，都存在非空开集V⊆p∑ω，使得V⊂L或V⊂Lc，则称L可监视。

因为存在BV={p∑ω|p∈∑*}，非空开集所以，V可以由基本开集B=q∑ω,p≤q来代替。

由文献[2]不难得到以下命题：

命题1可监视性质在有限交，有限并和补下封闭。

命题2开集和闭集可监视。

命题3L可监视当且L的边界有空的内部。

定义3（LTL的语法[10]）原子命题集合AP上的LTL公式根据下述语法形成：

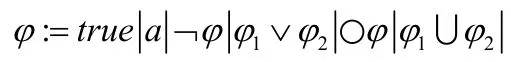
其中a∈AP。

定义LTL经常使用的公式如下：

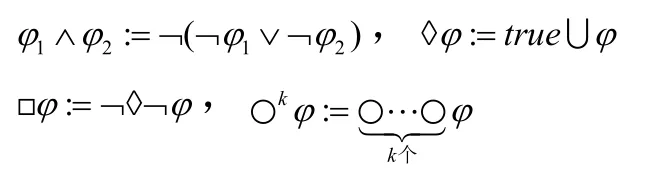
在本文中，令∑=2AP表示AP的幂集，并且把看做AP的任一包含的子集。

定义4（LTL的语义[10]）令φ是AP上的LTL公式，由φ诱导的性质为：

其中，满足关系|=⊆∑ω×LTL是具有表1 所示性质的最小关系。由LTL公式诱导的性质（语言）称为LTL性质（语言）。

表1 无限单词的LTL 语义

定义5（安全/余安全公式）[7]公式φ∈LTL称为一个安全（余安全）公式，若L（φ）是一个安全（余安全）性质。

3 LTL 性质的可监视性

定理1L（ture）可监视。

证明由于L（ture）=∑ω是拓扑空间中的既开又闭的集合，因此可监视。

定理2若a∈AP，则L（a）可监视。

证明由于，因此L（a）可监视。

由于L（﹁φ）=L（φ）c，并且可监视性在补下封闭，因此有：

定理 3对于φ∈LTL,L（φ）可监视当且仅当L（﹁φ）可监视。

由于L（φ1∨φ2）=L（φ1）∪L（φ2），并且可监视性在有限并下封闭，可得：

定理4对于φ1,φ2∈LTL，若L（φ1）和L（φ2）可监视，则L（φ1∨φ2）可监视。

由于

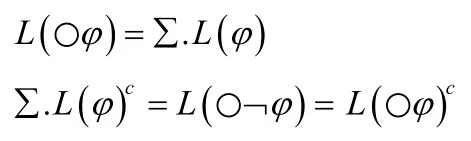
所以有：

定理5对于φ∈LTL，L（φ）可监视当且仅当L（○φ）可监视。

证明" ⇒"∀x∈∑ω，x=A0A1A2...=A0.z，其中A0∈∑,z=A1A2...∈∑ω，由于L（φ）可监视，对z∈∑ω，∀q=A1A2…Ak＜z（k≥1），（则p=A0.q可以是x的长度≥ 2的任意前缀），存在非空开集

（则A0.V⊆p∑ω）使得V⊆L（φ）或V⊆L（φ）c。因此，非空开集A0.V⊆∑.L（φ）或A0.V⊆∑.L（φ）c即A0.V⊆L（○φ）或A0.V⊆L（○φ）c。

" ⇐ "反证法。假设L（φ）不可监视，则∃y∈∑ω,∃p＜y，对任意非空开集V⊆p∑ω，都有V∩L（φ）≠∅并且V∩L（φ）c≠∅。对任意A∈∑，令x=A.y，则A.p＜A.y,∀A.V⊆A.p∑ω，有A.V∩∑.L（φ）≠∅并且A.V∩∑.L（φ）c≠∅，即A.V∩L（○φ）≠∅并且A.V∩L（○φ）c≠∅，从而，L（○φ）不可监视。矛盾。

从上述定理，易得如下推论：

推论1对给定的i∈N+和φ∈LTL，L（φ）可监视当且仅当L（○iφ）可监视。

前面已证，LTL公式的可监视性在取非、有限析取、有限合取和下一步算子下封闭。但是，在直到算子下不封闭，反例如下：

例1设AP={a},∑=2AP=｛｛a｝,∅｝。

φ1=true,φ2=﹁(ture∪a)，则L（φ1）,L（φ2）可监视，然而L（φ1∪φ2）不可监视。

由于