柱面共形阵列DOA与极化参数高效联合估计算法

2021-07-23齐子森彭大林宋佰霖

空军工程大学学报 2021年3期

齐子森，彭大林,2，许华，宋佰霖

(1.空军工程大学信息与导航学院，西安， 710077； 2.95865部队，北京， 102200)

信源方位与极化参数的耦合使得绝大多数高效DOA算法无法应用到共形阵列测向领域，成为了制约共形阵列天线测向算法发展的一个难题。传统的基于协方差矩阵估计和特征值分解实现噪声子空间估计的共形阵列测向算法普遍具有计算量大、适用性差的问题[1-4]。已有的共形阵列信源方位与极化参数的联合估计算法对噪声子空间的分析处理不够系统深入[5-7]。文献[8]通过对阵元局部坐标系进行3次欧拉旋转变换，实现了共形阵列天线的单元方向图指向的统一，给出了共形阵列天线阵列流形建模的方法。在此基础上，文献[9]通过信源方位与极化参数的去耦合降低了算法的复杂度，实现了信源方位与极化参数的联合估计，具有普适性好，计算量较小的特点。但是，由于噪声子空间依然是由传统特征值分解的方法获得，所以计算量依然很大。

文中借鉴经典线阵、面阵的高效子空间估计思想[10-14]，给出了一种基于快速子空间估计的柱面共形阵列天线信源方位与极化参数高效联合估计算法。

1 柱面共形阵列天线的数据模型

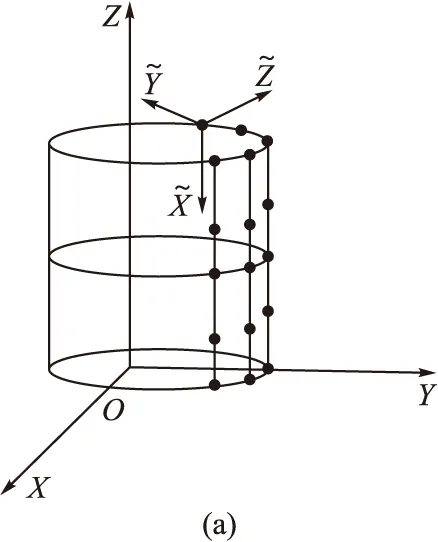
对于安装有N个阵元的柱面共形阵列天线(见图1)，在远场中有M个窄带独立的点源以平面波入射，加上噪声扰动后，阵列接收到的快拍数据可表示为：

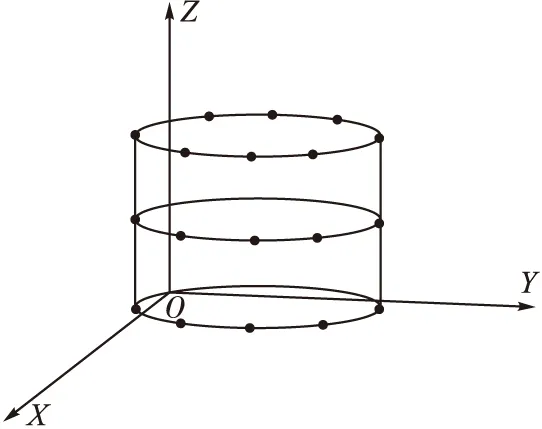
图1 柱面共形阵列天线

X=A(θ,φ)S+N

(1)

式中:X为N×1快拍数据矢量;S为M×1入射信号复幅度矢量;N为阵列噪声矢量;A(θ,φ)为N×M阵列的流形矩阵：

A(θ,φ)=[a(θ1,φ1),a(θ2,φ2),…,a(θM,φM)]

(2)

式中：a(θi,φi)为第i个信源的导向矢量，表示为：

a(θi,φi)=[r1(θ1,φ1)exp(-jk0p1•vi),

r2(θ2,φ2)exp(-jk0p2•vi),…,

rN(θN,φN)exp (-jk0pN•vi)]T

(3)

ri=gi·pl=giθ·kθ+giφ·kφ

(4)

gi=giθ(θ,φ)uθ+giφ(θ,φ)uφ

(5)

pl=kθuθ+kφuφ

(6)

uθ=cosθcosφux+cosθsinφuy+sinθuz

(7)

uφ=sinφux+cosφu

(8)

式中：ri为第i个阵元对单位强度入射信号的响应；gi为阵元的单元方向图；pl为来波信号的极化方式；pi表示第i个阵元在全局坐标系下的位置矢量，vi表示第i个信源在全局坐标系下的方位矢量，k0表示2π/λ0。

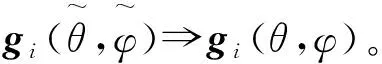
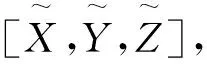
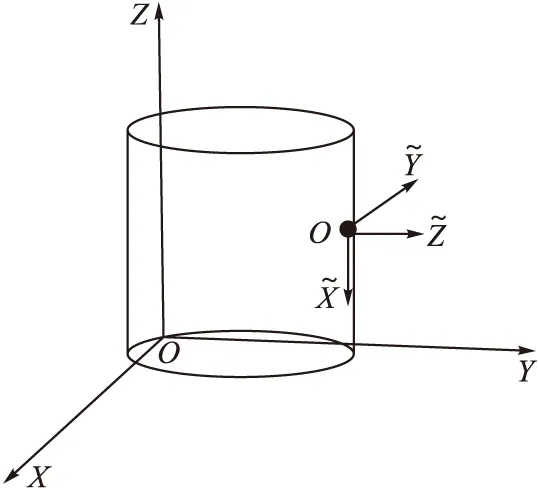
图2 全局直角坐标系与局部直角坐标系

为了实现阵元单元方向图的坐标系旋转变换，我们需要完成以下2个部分：

2)方向图正交极化分量变换阵列:

全局直角坐标系与阵元局部直角坐标系的旋转关系可以通过3次欧拉旋转变换得到，相应的欧拉旋转矩阵可以表示为[8]：

R(D,E,F)=E(X″,F)E(Y′,E)E(Z,D)=

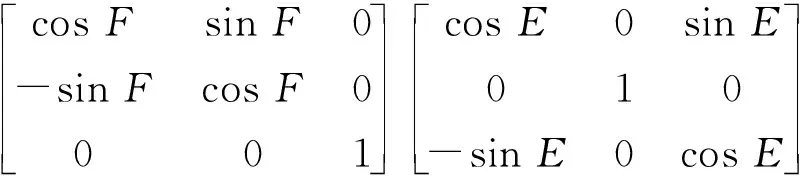
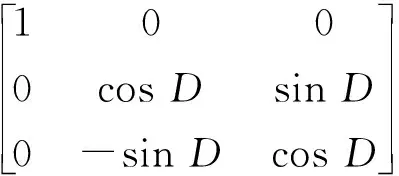
(9)

式中：E(Z,D)表示第1次旋转以Z轴为旋转轴，逆时针旋转角度D的欧拉旋转矩阵；E(Y′,E)表示第2次旋转以Y′轴为旋转轴，逆时针旋转角度E的欧拉旋转矩阵；E(X″,F)表示第3次旋转以X″轴为旋转轴，逆时针旋转角度F的欧拉旋转矩阵。通过合理选择3次欧拉旋转的旋转角度(D,E,F)，E(Z,D)，E(Y′,E)和E(X″,F)可以将阵元的全局直角坐标系旋转变换为阵元的局部直角坐标系。这种旋转变换适用于任何几何结构的共形阵列的阵元的坐标系变换，不同的几何结构的共形阵列在进行欧拉旋转变换时对应的欧拉旋转角度不同。

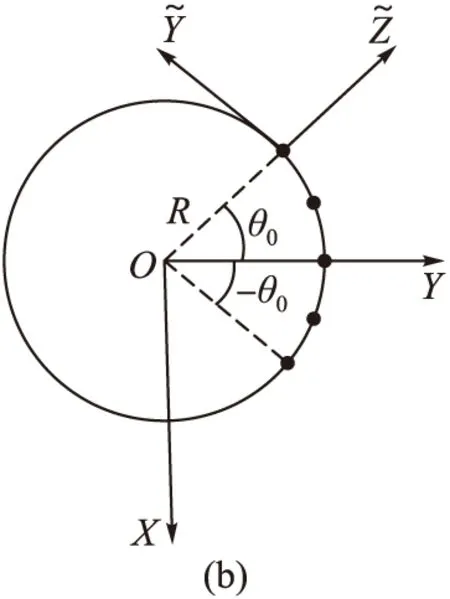
对于图3的柱面共形阵列天线，阵元对应的欧拉旋转角度为：

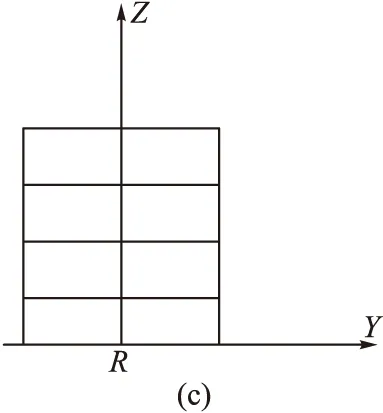
图3 柱面共形阵列阵元分布

(10)

式中：n为由下至上的圆阵的序号；m为每层圆环阵中逆时针方向阵元序号；N为圆阵的总层数；M为每层圆阵中阵元的总数。

利用式(10)得到的各阵元的欧拉旋转角度，可以实现柱面共形阵列阵元全局直角坐标系与局部直角坐标系的变换：

R(Dnm,Enm,Fnm)[xnm,ynm,znm]T

(11)

在全局极坐标系内(θ,φ)处的阵元的直角坐标可以表示为：

(12)

将式(10)、(12)代入式(11)可以实现阵元全局极坐标系到局部直角坐标系的变换：

[sinθnmcosφnm,sinθnmsinφnm,cosθnm]T

(13)

利用直角坐标系与极坐标系的变换关系，由旋转所得到的阵元的局部直角坐标得到文中所需要的局部极坐标系中的方位：

(14)

(15)

gnmθ(θ,φ)uθ(θ,φ)+gnmφ(θ,φ)uφ(θ,φ)

(16)

通过式(15)和式(16)的变换，实现了阵元极化方向图由局部极坐标系到全局极坐系的变换，通过这种变换，便可以建立起具有统一单元方向图指向柱面共形阵列的数学模型，为实现柱面共形阵列对信源方位与极化参数的联合估计奠定基础。

其中:

gnmθ(θ,φ)=(gnmXcosφ+gnmYsinφ)/

cosθgnmφ(θ,φ)=-gnmXsinφ+gnmYcosφ

(17)

将式(4)代入式(3)得：

(18)

aθ(θ,φ)=

[g1θexp (-jk0p1•v),…,gnθexp (-jk0pn•v)]T

(19)

aφ(θ,φ)=

[g1φexp (-jk0p1•v),…,gmφexp (-jk0pn•v)]T

(20)

忽略绝对相位信息，极化参数可表示为：

(21)

式中:k为任意实数;e-jδ(0<δ≤2π)为相位差。因此噪声扰动后的快拍数据也可以表示为：

X=AS+N=(AθKθ+AφKφ)S+N

(22)

S=[s1,s2,…,sm]T

(23)

N=[n1,n2,…,nm]T

(24)

Aθ=[aθ(θ1,φ1),aθ(θ2,φ2),…,aθ(θm,φm)]

(25)

Aφ=[aφ(θ1,φ1),aφ(θ2,φ2),…,aφ(θm,φm)]

(26)

Kθ=Im×m

(27)

Kφ=diag(k1e-jδ1,k2e-jδ2,…,kme-jδm)

(28)

式(22)～(28)中：A表示流形矩阵；S是信号矢量；N为加性高斯白噪声；θi,φi分别表示第i个入射信号的俯仰角与方位角。

2 柱面共形阵列天线信源方位与极化状态的高效联合估计算法

2.1 基于特征值分解的联合估计算法

柱面共形阵列输出数据的协方差矩阵：

R=E[XXH]=ARSAH+σ2I

(29)

对协方差矩阵R进行特征值分解：

(30)

式中：US和UN分别由M个大特征值和N-M个小特征值对应的特征矢量构成；ΣS和ΣN分别为M个大特征值和N-M个小特征值构成的对角阵。当快拍数L有限时，R的统计一致估计为：

(31)

根据子空间原理有：

(32)

将式(18)和(21)代入式(32)得[9]：

(33)

(34)

由秩损理论，当且仅当θ,φ取信源的真实方位时矩阵Q秩损，因此

(35)

umin=umin[Q]

(36)

进一步解得：

(37)

(38)

式中：umin[·]为求矩阵最小特征值对应特征向量的算子。

2.2 柱面共形阵列天线的快速子空间估计

对柱面共形阵列接收数据的协方差矩阵进行特征值分解：

(39)

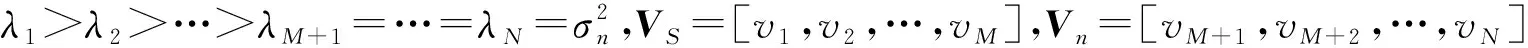
VS的列数等于信源协方差RS的秩M，从而张成A(θ,φ)的M维子空间，这里M表示信源数，由式(29)和式(39)得：

VS=AQ

(40)

式中：Q=RSAHVS(ΛS-σ23I)-1∈CM×M是满秩矩阵。

多级维纳滤波器的每一级匹配滤波器均是前一级期望信号与观测信号的互相关函数的归一化矢量，即:

(41)

且相互正交，所以级数为N的MSWF相当于维纳-霍夫方程在Krylov子空间即：

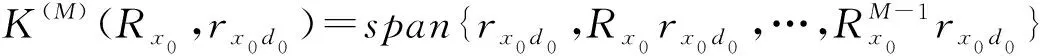
span{h1,h2,…,hM}=

(42)

所以存在一个满秩矩阵K∈CM×M，使得：

[h1,h2,…,hM]=

(43)

i=0,1,…,M-1

(44)

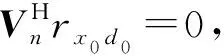
AQΓK=AH

(45)

其中:

∈CM×M

(46)

H=QΓK∈CM×M

(47)

因为Q和K均是非奇异矩阵，所以H也是非奇异矩阵。由式(45)可得：

(48)

(49)

即TS与信号子空间等价，Tn与噪声子空间等价。

2.3 基于多级维纳滤波器的联合估计算法

为了降低常规子空间估计的计算复杂度，最有效的方法就是避开协方差估计和特征值分解。事实上，当给定某一信号的波形，由多级维纳滤波器的前向分解就可以实现信号子空间和噪声子空间的快速估计[15]。

基于多级维纳滤波器构建噪声子空间的算法如下：

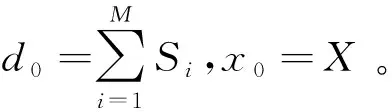
步骤2前向递推：

Fori=1,2,…,N

xi=xi-1-hidi

(50)

式中：di是各级期望信号；xi是各级观测信号。

信号子空间和噪声子空间由各级滤波器组成：

US=span{h1,h2,…,hM},

UN=span{hM+1,hM+2,…,hN}

(51)

后续步骤与2.1节算法相同。

综上所述，本文提出的基于多级维纳滤波器的柱面共形阵列天线信源方位和极化参数高效联合估计算法步骤总结如下：

步骤1获得目标点源的信号波形和柱面共形阵列天线接收到的快拍数据。

步骤2根据式(50)进行维纳滤波器的前向递推获得各级滤波器函数。

步骤3根据式(51)获得噪声子空间。

步骤4根据式(34)和(35)进行空间谱搜索获得目标方位。

步骤5根据式(36)、(37)和(38)进行目标信号的极化参数配对。

3 算法性能分析

3.1 算法复杂度分析与比较

文献[9]通过将信源方位与极化参数去耦合降低了谱峰搜索的维数，减小了运算量，但因为依然利用协方差估计和特征值分解的方法获得噪声子空间，所以利用柱面共形阵列实现参数联合估计所需的运算量为O(N3+N2L)，其中L为快拍数。本文在柱面共形阵列快拍数据构建噪声子空间的过程中因为只利用到了目标信号的波形和多级维纳滤波器的前向分解，并不涉及多级维纳滤波器的后向合成，更不涉及协方差的估计和特征值的分解，因此运算量为O(N2L)[15]。因此本文柱面共形阵列信源方位与极化参数联合估计算法更为高效。2种算法运算量对比见表1。

表1 算法运算量对比分析

进行仿真实验以验证本文提出的高效联合估计算法的性能。仿真实验中，假设在远场有2个独立、窄带、方位分别为θ1=30°、φ1=90°、θ2=60°、φ2=120°，极化参数完全相同，垂直水平极化模值和相位差分别为k1=1、k2=2、δ1=π/4、δ2=π/3的信源以平面波入射到如图3的柱面共形阵列，图中每层阵元间隔半波长，柱面横截面半径为2倍波长。在小样本支撑的信号环境中，本文算法具有对文献[9]联合估计算法计算量上的明显优势，因此实验中2种算法采用不同的快拍数进行仿真对比。

1)实验1角度估计的速度仿真

联合估计算法的高效性通过角度估计速度可以比较直观地反映出来。在本实验中，角度估计速度利用在不同信源数条件下的角度估计时间来衡量，实验中取蒙特卡罗实验运行时间的平均值作为单次估计时间。

仿真条件：信噪比设为15 dB，蒙特卡罗实验次数为2 000，文献[9]快拍数为3 000，本文算法快拍数设为3 000，阵元数由20变化到100，估计时间和阵元数关系的仿真如表2所示。

由表2可以看出，在整个阵元数的变化范围内，本文高效联合估计算法的单次估计时间始终低于文献[9]算法的单次估计时间，并逐渐拉开时间上的差距，验证了本文算法在计算量上的优势，证明了本文算法相对于以往联合估计算法的高效性和巨大的实用价值。

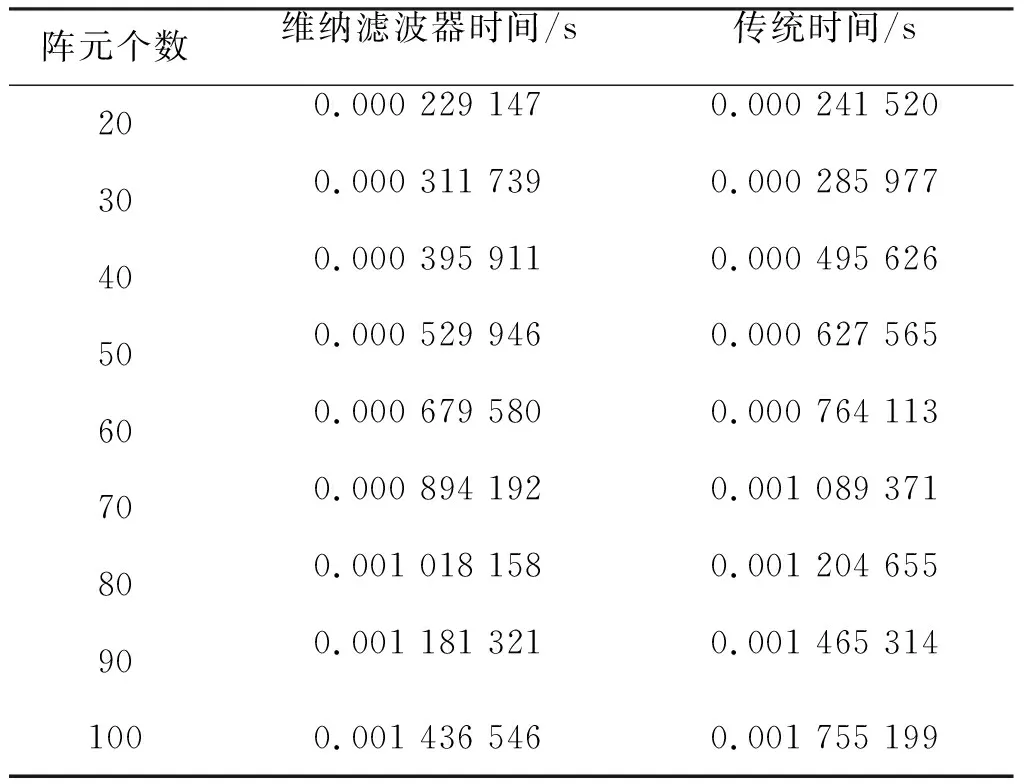
表2 算法运算量对比分析

2)实验2均方根误差的仿真

算法的均方根误差随信噪比的变化情况可以反映算法的估计精度。

仿真条件：文献[9]快拍数设为500，本文高效算法快拍数设为500，蒙特卡罗实验次数设为500，信噪比由-5 dB变化到15 dB，仿真结果如图4所示。

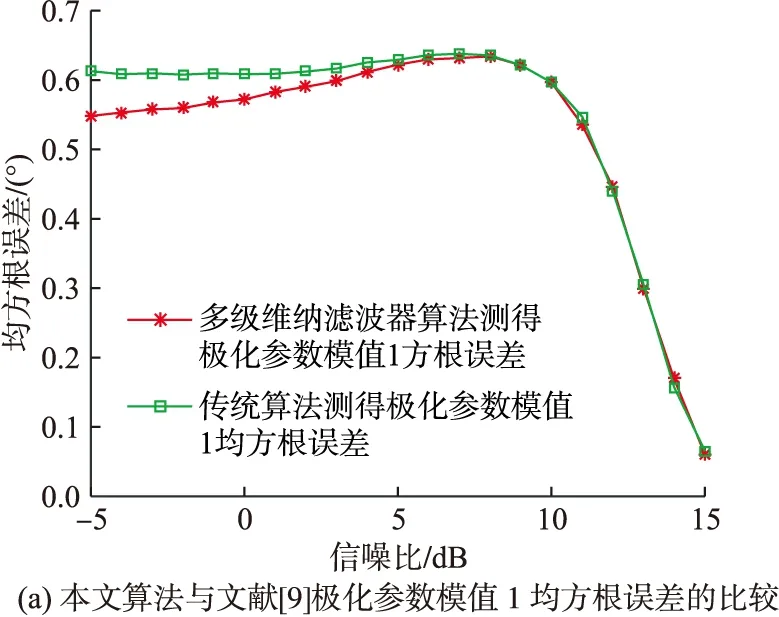
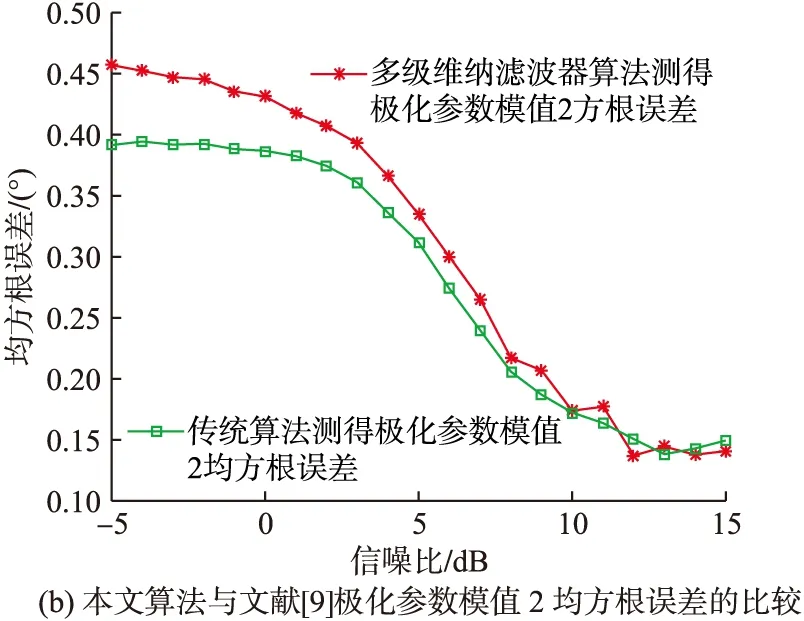
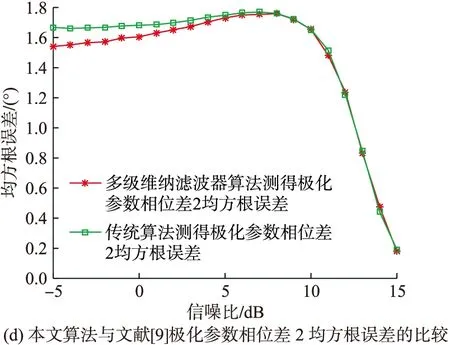
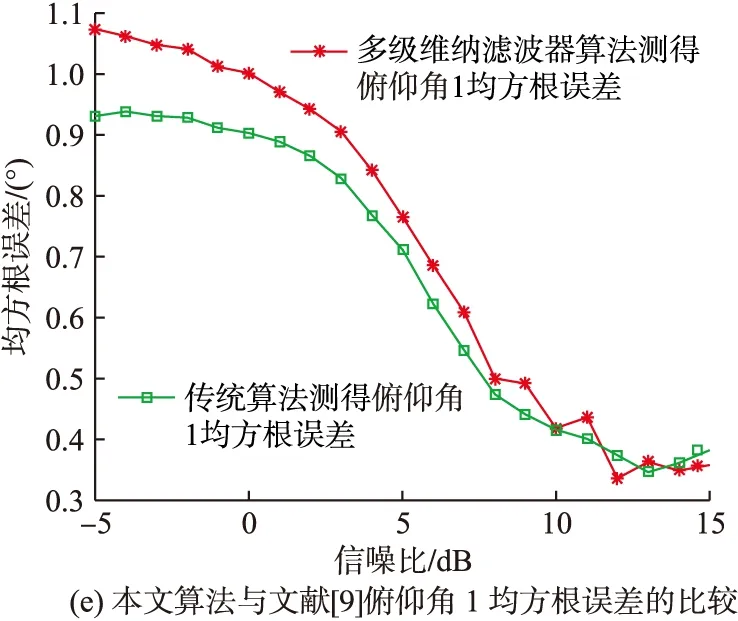
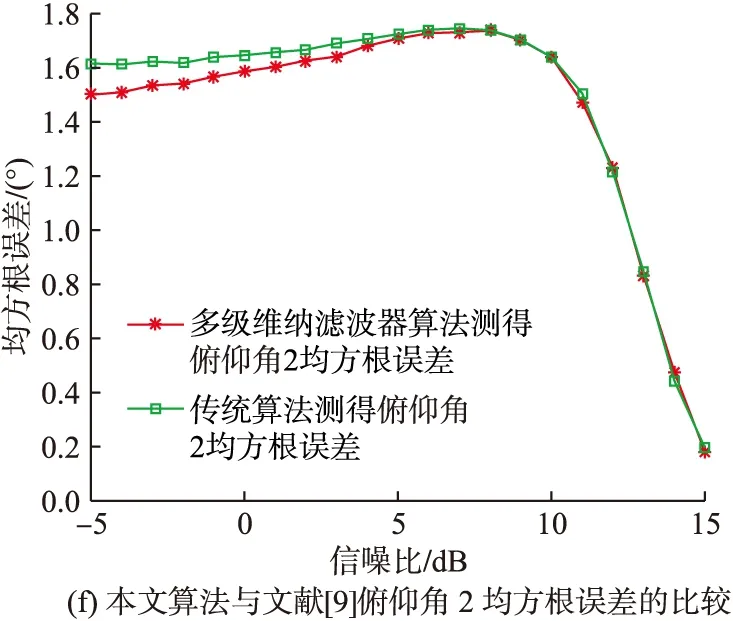
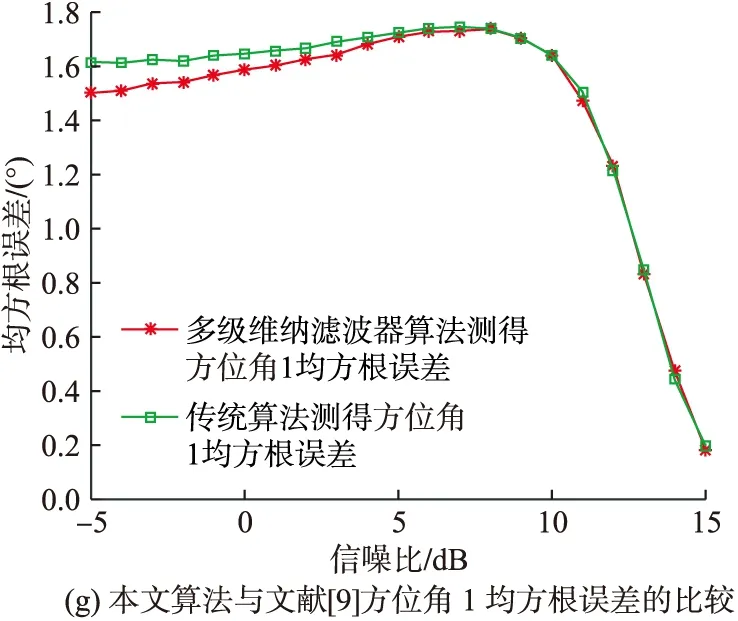
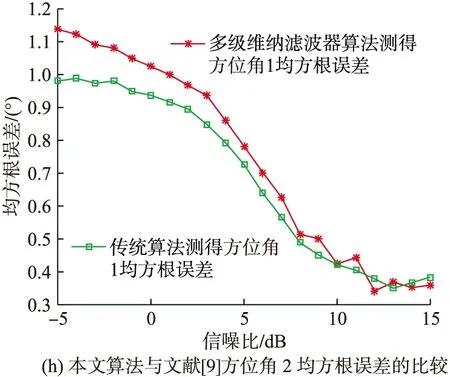
图4 均方根误差与信噪比的关系

由图4可以看出，在整个信噪比的变化范围内，本文的高效联合估计算法对极化参数和来波方位的估计值均方根误差与文献[9]算法估计值均方根误差大致相当，说明在一定的信噪比变化范围内，本文的高效联合估计算法的估计精度与文献[9]算法的估计精度大致相当。此外，在信噪比大于10 dB的条件下，本文算法对各项参数(极化参数相位差除外)的估计均方根误差均小于1，这样的估计精度在大多数工程应用中是可以被接受的。

综上分析，在一定的估计精度要求下，本文的联合估计算法在小样本支撑的信号环境中对严重依赖信号样本数保证估计精度的文献[9]具有计算量上的一定优势，但也依然存在一些不足：计算优势严重依赖快拍数、计算精度受制于快拍数和阵元数过多也会减小本文高效算法的计算优势。