面向多机协同的Att-MADDPG围捕控制方法设计
2021-07-23魏瑞轩姜龙亭
刘 峰, 魏瑞轩, 丁 超, 姜龙亭, 李 天
(空军工程大学航空工程学院, 西安, 710051)
无人机集群是一种新型作战样式,具有作战成本低、冲突胜算大、生存能力强、作战效能高的特点。这些重要特征使得无人机集群在局部冲突中扮演着越来越重要的角色[1-2]。协同围捕问题属于无人机集群作战的典型应用场景之一,有重要的理论研究价值和广泛的应用前景。
在协同围捕方法设计上,已有不少学者做了相关研究[3-7]。张红强等[3]设计了一种基于简化虚拟受力模型,借助势域函数使机器人在未知动态环境下完成围捕。李瑞珍等[4]采用协商法为机器人分配动态围捕点,建立包含围捕路径损耗和包围效果的目标函数并优化航向角,从而实现协同围捕。Michael Rubenstein等[5]以1 000个机器人为载体,分边缘检测、梯度上升、协同定位3部分算法设计,并通过局部交互进行合作,完成给定图片的不规则图形围捕演示,以人工集群的手段汇聚出自然蜂群的能力。
以上研究均是基于分布式控制,将协同围捕问题转换为集群任务分配、路径规划、群体一致性问题,从而达到围捕的效果,但在群体智能涌现方面仍有待提升。
近年来,也有部分学者探索通过强化学习方法来解决协同围捕问题[8-10]。吴子沉等[8]将围捕行为离散化后,设计能够应对复杂环境的围捕策略,但其存储机制仍有待优化。陈亮等[9]提出混合DDPG算法,有效协同异构agent之间的工作,同时,Q函数重要信息丢失及过估计等问题有待解决。Ryan Lowe[10]于2017年提出MADDPG算法,采用“集中训练,分散执行”的框架解决了环境不稳定的问题,但是该算法随着agent数目的增加,Actor-Critic网络难以训练和收敛。
针对以上分析,本文提出一种多无人机协同围捕算法Att-MADDPG(即Attention-MADDPG)。
1 问题描述
1.1 围捕环境描述
在一个无限大且无障碍的二维环境中,随机分布n(n≥3)架围捕无人机Ui和一架目标无人机T,其速度分别为vi、vT,且满足vi>vT,航向角分别为φi、φT,其中i∈In={1,2,…,n},如图1所示。
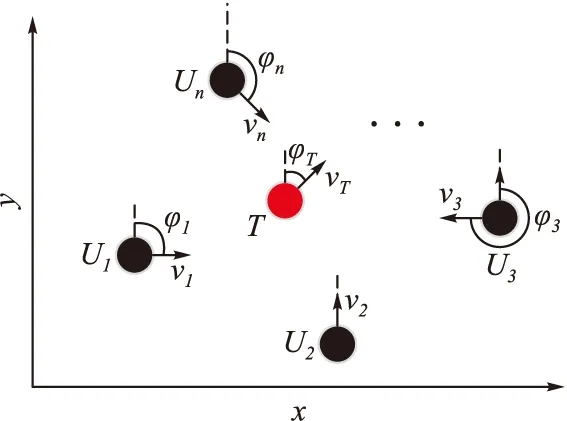
图1 围捕环境示意图
假设对于任意无人机,都能将自身的参数通过通信网络G实现与其他无人机实时信息交换。本文的目的就是基于这种信息共享,设计控制方法,使n架围捕无人机通过协作,在有限时间t内,在目标无人机周围形成围捕包围圈,迫使目标无人机T停止运动,从而完成围捕任务。理想的围捕包围圈通常是围捕无人机群均匀分布在以目标无人机T为圆心,围捕半径r的圆上[5],以n=4为例,理想的围捕包围圈如图2所示。
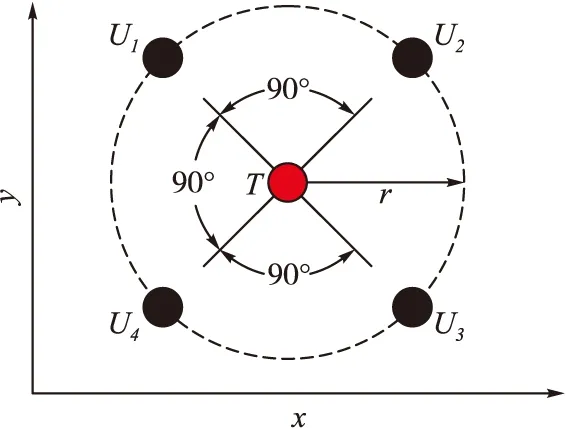
图2 围捕包围圈示意图
1.2 围捕无人机模型
设无人机i当前时刻的位置为[x,y]T,构建非线性运动学方程如下:
(1)
式中:ui为无人机的控制输入,ui∈[-ω0,ω0];ω0为无人机角速度上限。围捕控制策略就是根据围捕态势确定每架无人机的ui,使围捕无人机集群实现对目标无人机的有效围捕。
2 基于强化学习的MADDPG算法
2.1 强化学习理论
强化学习(reinforce learning,RL)是机器学习的一种,不同于监督学习或无监督学习,强化学习是通过与环境的交互进行不断试错-学习,以达成回报最大化或实现特定目标,如图3所示。

图3 智能体与环境交互图
强化学习的常见模型是标准的马尔可夫决策过程(markov decision process,MDP)。由四元组〈S,A,R,Ps,a〉表示,其中,S表示状态集,A表示动作集,R表示奖励函数,Ps,a表示状态转移概率。基于当前状态st,执行动作at,以一定的状态转移概率达到下一时刻状态st+1,获得即时奖励Rt,但强化学习是寻找最大化累积回报的学习过程[11]。定义累积奖励期望值Qπ(s,a):
(2)
式中:γ为折扣因子,0<γ≤1,表示注重长期奖励的程度。π为策略,即状态到动作的映射。给出Q-Learning算法中Q值迭代计算表达式:
Q(st,at)←Q(st,at)+α[Rt+γmaxQ(st+1,at+1)-Q(st,at)]
且st状态下最优策略为:
Dietterich.T.G[12]从值函数分解的角度,完成了Q-Learning算法中Q值累加的收敛性证明。
2.2 MADDPG算法
多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient,MADDPG)是对深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法进行拓展,使其能够适用于传统强化方法无法处理的多智能体合作问题的一种智能算法[10]。MADDPG算法采用“集中训练,分散执行”的框架进行学习,见图4。

图4 MADDPG算法流程图
每个agent拥有一套独立的Actor-Critic网络,其中Actor为行动网络,Critic为评价网络。在训练过程中(图4中红色部分),每个agent的Critic获取全信息状态,同时包含所有agent的动作。当模型训练完毕,每个agent的Actor利用局部信息完成与环境的交互(图4中蓝色部分)。令Ot表示agent对环境的观测,IA和at分别表示Actor的输入和输出,IC和Qi分别表示Critic的输入和输出,那么对于第i个agent,网络输入输出为:
IA=Ot,at=πi(st)
IC=[Ot,a1,a2,…,an],Qi=Qi(IC)
(3)
当agent数量增多时,由式(3)中IC可知,Critic的输入维度也呈线性增长,这将导致网络难以训练和收敛。文献[10]和[13]同样指出,尽管集中训练,分散执行的结构具有诸多优势,但是随着agent数量的增加,集中训练中Critic网络规模会快速增长,因而无法处理大规模多智能体的学习问题。同样的,由Facebook AI实验室和Google AI联合赞助的二维网格环境炸弹人平台,在测试时最多也只能容纳4个agent。
3 基于Att-MADDPG的围捕控制策略设计
3.1 面向无人机围捕的Attention机制
近年来,注意力机制(attention mechanism)被广泛用于基于深度学习的自然语言处理、图像分类、机器翻译可视化对齐、语音识别等各种任务中,并取得了不错的效果[14]。2017年6月,Google机器翻译团队借助自注意力机制在WMT2014语料中的英德和英法翻译任务上取得了优异成绩,翻译错误率降低了60%,并且训练速度远优于其他主流模型[15]。
围捕过程中也存在类似的注意力问题。每架无人机更多的关注与自己近邻的无人机,对距离较远的无人机的态势关注的较少,甚至不关注。这就是围捕过程中的注意力现象。我们将这种现象引入到围捕策略的设计,形成面向围捕的注意力机制。以无人机协同围捕的场景程阐释注意力机制如下:
定义围捕无人机集群的联合动作为Source,待处理信息为Target:
Source=〈p1,p2,…,pm〉
Target=〈q1,q2,…,qn〉
其中,pi(i=1,2,…,m)表示第i架无人机动作,qi(i=1,2,…,n)表示待处理信息。Attention机制[16-17]最常用的是编码器-解码器(Encoder-Decoder)框架,如图5所示。Encoder对输入的Source进行编码,通过神经网络的非线性变换转化为注意力分布C,C={c1,c2,…,cLp},其中Lp为Source的长度,Decoder根据注意力分布C和n-1时刻无人机的位置生成n时刻的信息qn,即围捕无人机集群待处理信息。给出注意力分布ci(i=1,2,…,Lp)的表达式:

图5 基于Attention机制的Encoder-Decoder框架
qn=Attention(ci,qn-1)
(4)
式中:wij为Source中第j架无人机的注意力权重系数;pj为Source中第j架无人机的动作信息;Attention为非线性变换函数。
给出基于Attention机制下注意力分布ci的具体计算过程:
1)计算2架围捕无人机之间的相关性系数:Similarityi=ln(Distanceij/D),其中Distanceij为两架围捕无人机之间距离,D为有效利用区域半径。
2)引入Softmax函数对第1阶段的相关性系数进行归一化处理,得到注意力权重系数ωi。一方面将原始分值映射成所有元素权重之和为1的概率分布,另一方面通过Softmax的内在机制突出重要元素的注意力权重系数。
(5)
3)根据注意力权重系数对围捕无人机信息进行加权求和,计算注意力分布ci值。
3.2 基于Att-MADDPG的围捕控制策略
本文2.2节中分析MADDPG算法由于IC的计算中使用了所有agent的信息,使得其训练收敛受到影响。因此,我们引入Attention机制对信息进行注意力筛选,从而提高信息的有效利用率,算法框图如图6所示。
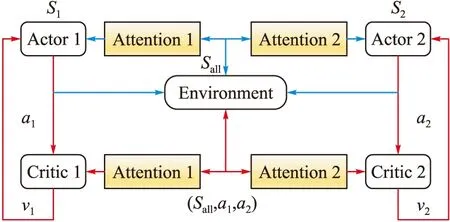
图6 基于Attention机制改进的MADDPG算法框图
与MADDPG算法不同之处在于中心化的大脑(即Critic)协调所有围捕无人机的动作之前,经各自Attention模块进行非线性处理,对有效利用区域内的围捕无人机信息进行策略评估(图6中红色部分所示)。当模型训练完毕,依据Actor利用局部信息完成与环境的交互(图6中蓝色部分所示)。则围捕无人机i的有效利用区域值函数为:
因此,每架围捕无人机的Critic网络拟合的是有效利用区域的全局值函数,而非围捕无人机自身的值函数。这样,只需要围捕无人机的策略朝着有效利用区域的全局值函数的方向更新即可。使用MADDPG算法中双网络进行更新:
(6)
式中:yi为目标网络的值函数,由即时奖励和下一步确定策略值函数构成;L(θi)为目标Critic网络损失函数,θi为网络中参数集合。目标Actor网络和目标Critic网络采用周期性平稳滑动方法从Actor-Critic网络中复制参数进行更新。目标Critic网络损失梯度通过链式法则进行求导,其梯度为:

(7)
式中:状态s为有效利用区域全局观测;si为围捕无人机自身观测。Att-MADDPG算法流程见图7。

图7 Att-MADDPG算法流程图
Att-MADDPG算法伪代码如下所示:

初始化环境参数、参数变量;判断是否围捕成功;for episode=1 to Mdo 初始化随机噪声N; 初始化围捕无人机状态S; fort=1 to max-episode-length do 每架围捕无人机采用随机策略执行一次动作A,与环境交互后得到即时奖励R,并达到新的状态S'; 存储
4 仿真实验
为验证所设计Att-MADDPG算法的有效性及智能性,取围捕无人机数量n=4进行动态协同围捕仿真实验,并对比MADDPG算法进行训练,测试相关性能指标。
4.1 仿真环境配置
设置围捕无人机奖励函数如下:

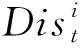
仿真环境参数设置如表1所示。

表1 仿真场景设置
配置相同的四机协同围捕环境,设置相同的奖励函数,MADDPG算法及Att-MADDPG算法的训练过程如图8~9所示。如图8所示,采用MADDPG算法训练的围捕无人机集群大致完成协同围捕任务,但训练过程中仍存在一些片段无法有效围捕。

图8 MADDPG算法训练过程图
由图9可知,经过训练,Att-MADDPG算法的平均奖励在150片段后收敛,并大致均匀分布570左右,围捕无人机集群能够有效完成协同围捕任务,并获得较高奖励。
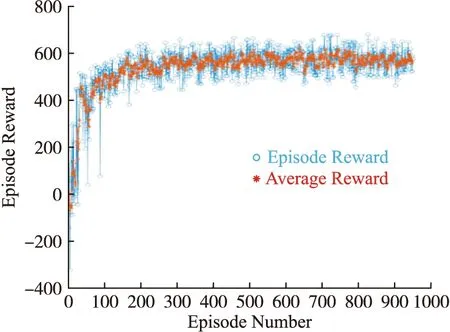
图9 Att-MADDPG算法训练过程图
引入Att-MADDPG算法及MADDPG算法在稳定收敛后1 000个片段的均方差,对比验证算法的稳定性,见表2。Att-MADDPG算法较MADDPG算法在协同围捕上更加稳定,根据3σ原则,记录稳定收敛后1 000个片段不在此范围内的平均奖励数目,见表3,Att-MADDPG算法稳定性较MADDPG算法提高8.9%。

表2 稳定收敛后1 000个片段的均方差

表3 1 000个片段内不在3σ原则范围内的数目
4.2 动态协同围捕仿真验证
设定目标无人机的运动策略为固定直线轨迹,对经过Att-MADDPG算法训练后的4架智能围捕无人机进行验证,验证集参数见表4。

表4 动态协同围捕验证集参数
由图10可知,围捕无人机通过相互协作完成围捕。在围捕过程中,无人机实时判断围捕态势,引入注意力机制观察有效利用区域半径内的其他无人机状态信息,达到形成围捕包围圈的目的,各无人机经过协作使系统涌现出更加智能化的协同围捕行为。

图10 动态协同围捕轨迹图
环境配置相同,采用MADDPG算法进行验证,Att-MADDPG算法完成协同围捕总用时264 s,MADDPG算法本文算法总用时326.4 s,减少19.12%。
5 结论
无人机集群作战在局部冲突中发挥着越来越重要的作用,协同围捕是无人机集群作战的典型应用场景之一,也是集群作战中的重要问题。本文针对MADDPG算法随着agent数量的增加,训练难以收敛的不足,基于注意力机制提出Att-MADDPG围捕控制方法,较MADDPG算法的训练稳定性提高8.9%,任务完成耗时减少19.12%,且经学习后的围捕无人机通过协作配合使集群涌现出更具智能化围捕行为。
为使本文所提算法能够适用于更加复杂的环境,仍需研究基于群智汇聚的协同围捕机理,并优化在三维环境下的协同围捕策略,使围捕行为更具智能化。
