基于显式有限元的转子不平衡与轴承故障耦合分析

杨子臻，左彦飞，邵化金，冯坤

(北京化工大学 a.发动机健康监控及网络化教育部重点实验室；b.高端机械装备健康监控与自愈化 北京市重点实验室，北京 100029)

据统计,旋转机械80%以上的转子振动故障由转子不平衡引起[1]，30%的旋转机械故障是由轴承故障引起[2]。在转子-轴承系统中，转子不平衡与轴承故障同时存在的情况时有发生，且会引发严重的机械振动，影响机组的正常运行,故有必要对转子不平衡与轴承缺陷耦合故障的特征及机理进行研究。

在对转子-轴承系统进行受力分析的基础上，基于仿真技术模拟系统工作状态，并对其进行计算分析，是研究系统特性的重要手段。国内外对轴承仿真技术做了大量研究：文献[3]基于LS-DYNA研究了深沟球轴承动态应力变化及各零件间的接触力，结果表明球与外圈接触力的波动大于内圈,球与保持架间的作用力较小；文献[4]研究了外圈故障状态下轴承各零件的等效应力，并得到外圈故障特征频率；文献[5]研究表明，随着轴承外滚道缺陷尺寸的增大，系统振动幅值随之增大；文献[6]指出滚子与滚道之间因离散化而产生的冲击及高频噪声是影响仿真结果准确性的重要原因；文献[7]提出了一种径向轴承准静态载荷分布和刚度的计算方法，并得到只有缺陷位于轴承受载区时才会存在故障冲击现象的结论;文献[8]基于有限元法分析了转子-轴承系统不平衡-不对中-碰磨耦合故障的振动响应，并微分耦合经验模态分解法，有效地完成了系统振动响应的分解，为各耦合故障征兆的获取提供基础；文献[9]分析了不平衡与碰磨故障耦合下转子-轴承-机匣系统的动态响应规律。

上述关于轴承有限元仿真的研究往往忽略转子的影响，只针对轴承进行仿真分析。关于转子-轴承系统耦合故障的研究多是转子多故障耦合研究，对于轴承故障与转子不平衡耦合研究较少。鉴于此，在对转子不平衡与轴承故障耦合各状态受力分析的基础上，基于虚位移原理的增广拉格朗日法建立轴承运动控制方程，运用LS-DYNA建立转子-轴承系统二维显式动力学有限元模型，开展转子不平衡与轴承外圈故障耦合状态下的故障特性机理分析。

1 转子-轴承耦合系统模型

轴承运动过程中各零件间存在复杂的力学关系，在故障耦合状态下轴承受力更复杂，受力情况如图1所示，图中:FCNi,FCNe分别为内、外圈滚道与滚子的法向力，FCji，FCje分别为内、外圈滚道与滚子的摩擦力，FCNc，FCjc分别为保持架对滚子的法向力与摩擦力，Gb为滚子重力，ωb为滚子转速。在无缺陷状态，滚子受内、外圈的作用力，通过内圈与滚子的摩擦使滚子沿外圈滚道滚动，滚子与保持架接触，驱动保持架自转。在进缺陷状态，滚子与内圈失去接触(驱动力)，滚子自转频率降低，其在自身公转方向一侧与保持架失去接触。在出缺陷状态，滚子在公转反方向一侧与保持架接触，使滚子撞击缺陷边缘产生冲击力。

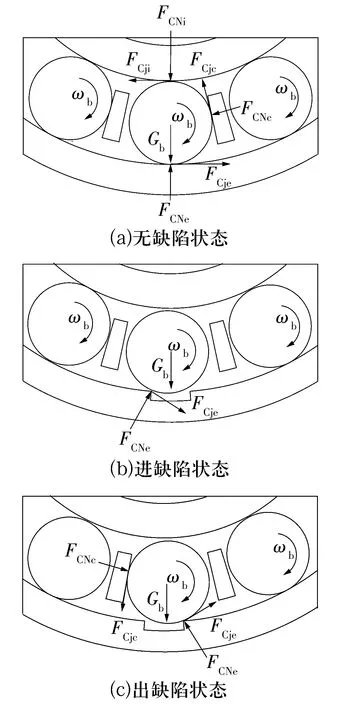
图1 不同状态下轴承受力分析简图

在对轴承-转子系统受力分析的基础上，基于虚位移原理的增广拉格朗日法建立轴承-转子耦合系统数学模型，即

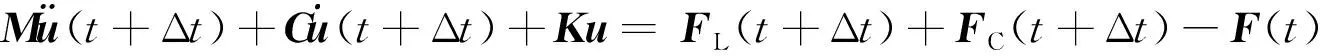
(1)

基于中心差分法求解轴承控制方程，即

(2)

(3)

将(2)，(3)式代入(1)式可得

(4)

FC(t+Δt)=FCj(t)-Ku+FCN(t+Δt)。

(5)

2 有限元模型

以N205圆柱滚子轴承为例分析，其主要结构参数为：外径52 mm，内径25 mm，滚子组节圆直径38.5 mm，滚子数量13，滚子直径7.5 mm，滚子长度7.5 mm。

假设外圈存在缺陷，外圈滚道预置长度为2 mm、深度为0.2 mm的贯穿缺陷。忽略轴承径向游隙、油膜以及材料塑性变形的影响，建立缺陷轴承模型。对模型进行网格划分，轴承各零件接触面网格细化，模型包含36 620个单元， 39 296个节点，网格划分如图2所示。

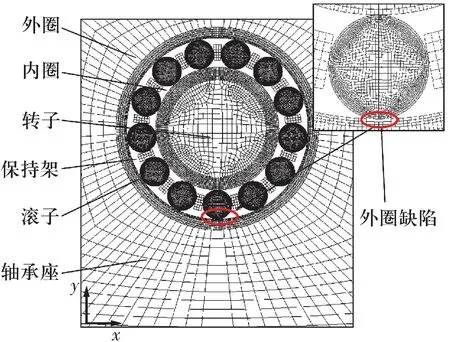
图2 转子-轴承系统网格划分

对轴承座底部施加全约束。滚子与内圈、滚子与外圈、内圈与转子、外圈与轴承座之间施加相应摩擦接触。在转子中心施加沿y轴负方向30 N的径向力，模拟转子所受重力。在转子中心施加60 N与转频同频的旋转径向力，模拟转子不平衡。模型施加重力加速度，在转子中心逆时针方向施加900 r/min的转速。

3 转子-轴承系统故障耦合特征

3.1 加速度

依据文献[10]求得滚子公转频率fc为6.06 Hz，外圈通过频率fbpfo为78.75 Hz。当仅存在外圈故障时，提取模型轴承座顶部中心节点的加速度信号(图3)，其时域波形中存在明显的冲击现象，相邻冲击间隔约0.013 s(77 Hz)，与外圈通过频率fbpfo(78.75 Hz)基本一致，且包络谱中也存在与外圈通过频率相近的79 Hz及其倍频成分。

转子不平衡-轴承故障耦合状态下轴承座节点加速度的时域波形及包络谱如图4所示。

图3 外圈故障时轴承座节点加速度信号的时域波形及包络谱

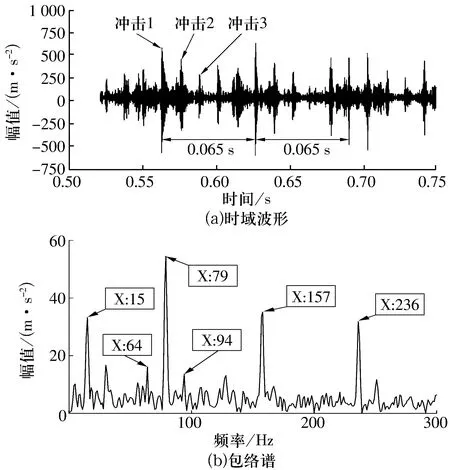
图4 耦合状态下轴承座节点加速度信号的时域波形及包络谱

由图4可知：在故障耦合状态下，时域波形中不仅存在时间间隔为0.013 s(78.75 Hz)的冲击现象，且幅值变化周期为0.065 s(15.3 Hz)，包络谱中不仅存在转频(15 Hz)与外圈故障特征频率(78.75 Hz)的单一故障特征，且外圈通过频率两侧存在差值为转频的边频带(64 Hz与94 Hz)。

3.2 转子轴心轨迹

耦合状态下转子轴心运动轨迹如图5所示，由图可知：1)轴心轨迹呈椭圆形且轨迹中心处于轴承几何中心的下方，轴心轨迹上半部分较为平稳，下半部分存在突变(区域1～4)。2)相邻偏移位移峰值的时间间隔为0.065 s(15.3 Hz)，与不平衡故障使转子产生正进动的频率(15 Hz)一致。3)区域1～2，3～4的时间间隔均为0.013 s(77 Hz)，与外圈通过频率fbpfo(78.75 Hz)相对应。

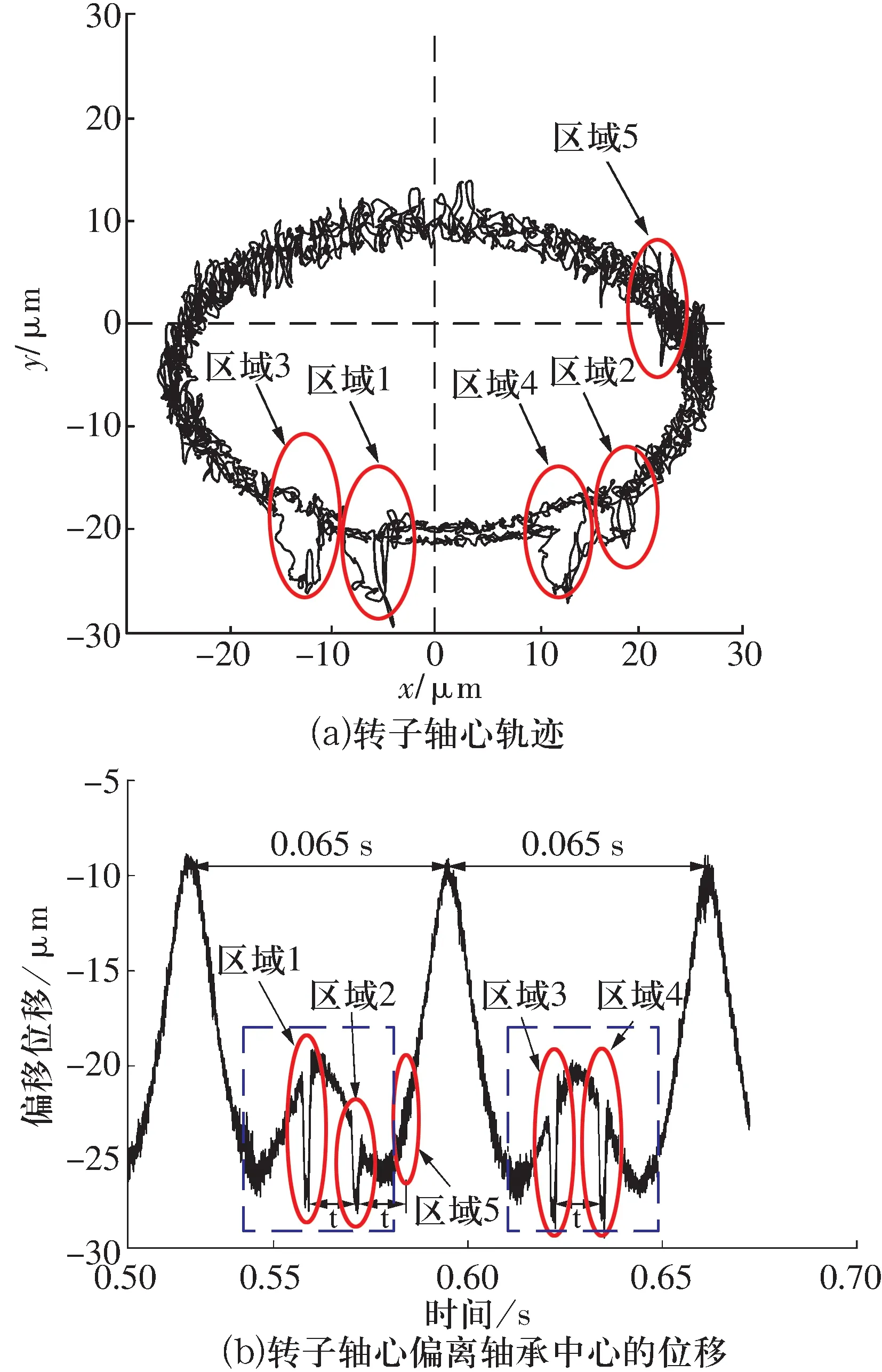
图5 耦合状态下转子轴心运动轨迹

4 转子-轴承系统故障耦合作用机理

在0.560，0.573，0.586 s时轴承的等效应力云图如图6所示，由图可知：1)随轴承运转，受载区逆时针旋转，逐渐远离外圈缺陷位置。2)结合图4a，冲击1，2，3分别对应1#，2#，3#滚子通过缺陷时产生的冲击。

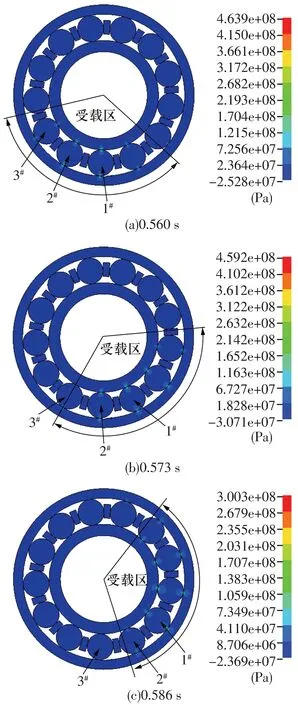
图6 轴承等效应力分布图

1#滚子通过故障时其质心偏离轴承节圆距离及与外圈的接触力如图7所示,由图可知：1)进缺陷阶段，滚子运动平稳，滚子与外圈的接触力逐渐减小为0，该阶段不存在碰撞。2)缺陷中阶段，滚子进入故障后做类平抛运动，滚子与外圈接触力为0，此时保持架驱动滚子沿周向运动，自身离心力使滚子产生径向运动。3)出缺陷阶段，滚子运动轨迹突变，与外圈接触力较为复杂，这是由于在此阶段发生了故障冲击，出缺陷时滚子撞击外圈缺陷边缘后反弹，与外圈失去接触的同时撞击内圈，然后回弹再次撞击外圈，如此循环，滚子在内外圈间撞击时产生的接触力大于滚子初次撞击外圈缺陷边缘时的接触力。

图7 1#滚子质心运动轨迹及其与外圈的接触力

图7中位置1,2,3处的接触应力如图8所示,由图可知：1)滚子撞击外圈缺陷边缘，最大接触应力出现在滚子与外圈故障边缘撞击处。2)滚子撞击外圈后反弹，与外圈失去接触的同时撞击内圈，其最大接触应力出现在滚子与内圈接触区域。3)滚子撞击内圈后，再次撞击外圈，最大接触应力出现在滚子与外圈撞击处。

图8 不同时刻1#滚子接触应力分布图

外圈出缺陷位置边缘处的冲击应力如图9所示，由图可知：1#,2#,3#滚子通过缺陷时均会产生冲击力，每个滚子出缺陷阶段第1次冲击时的应力基本相同，在内外圈之间跳动时产生的冲击力会随滚子处于受载区位置而变化。冲击应力幅值与图4a加速度时域波形中冲击幅值呈正相关，说明耦合状态下加速度时域波形中冲击幅值主要在滚子出缺陷阶段产生。每次冲击力后均出现波动，并出现负值，这是由于单元受撞击之后会产生应力波，致使单元受力方向发生变化，这也解释了图6及图8所示应力云图在碰撞接触位置附近出现负值的原因。

图9 外圈出缺陷边缘处的冲击应力

1#，2#，3#滚子质心运动轨迹及其与内圈接触力随时间的变化如图10所示。

由图10可知：1)0.559～0.562 s对应图5中的区域1。在0.559 s时1#滚子进入缺陷，与内圈的接触力变为0，滚子质心迅速下移，2#，3#滚子与内圈的接触力均在此刻增大，滚子质心出现下移，这是由于1#滚子与内圈失去接触导致受载滚子数发生突变，引起载荷再分配。0.562 s时，1#滚子处于出缺陷阶段，1#滚子受内外圈同时作用，再次成为受载滚子，引起载荷再分配，使转子恢复0.559 s前的运动轨迹，即图5中区域1呈现的转子轴心轨迹。2)0.572～0.575 s对应图5中的区域2，由于2#滚子处于承载区，其质心偏移位置及其与内圈接触力的变化情况与0.559～0.562 s时1#滚子类似，区域2表现出与区域1类似的变化。3)0.585～0.588 s对应图5中的区域5，此时3#滚子处于受载区外，其与内圈接触力在通过缺陷前后始终近似为0，对转子轴心轨迹不会产生显著影响，故3#滚子通过故障时质心虽然出现了下移，但1#，2#滚子质心轨迹及接触力基本没有变化，这解释了图5中区域5转子轴心轨迹未发生突变的原因。

5 试验验证

为验证文中仿真结果，搭建轴承故障模拟试验台，如图11所示。采用灵敏度为100 mV/g(g取9.8 m/s2)的加速度传感器，传感器量程为±50g,数据采集器采样率设置为51.2 kHz，在轴承座位置采集系统振动加速度信号，并基于MATLAB对其进行分析处理。

图11 轴承故障模拟试验台

转子不平衡与轴承外圈故障耦合状态下的加速度时域波形及包络谱如图12所示，由图可知：时域波形中故障冲击时间间隔为0.012 5 s，且冲击幅值以0.062 5 s为周期变化，包络谱中存在15.3 Hz和79.7 Hz的频率成分，其分别对应转频(15 Hz)及外圈通过频率(78.75 Hz)，且外圈通过频率两侧存在差值为转频的边频带(64.4 Hz与95 Hz)。试验结果与仿真结果具有良好的一致性，证明了仿真结果的有效性。

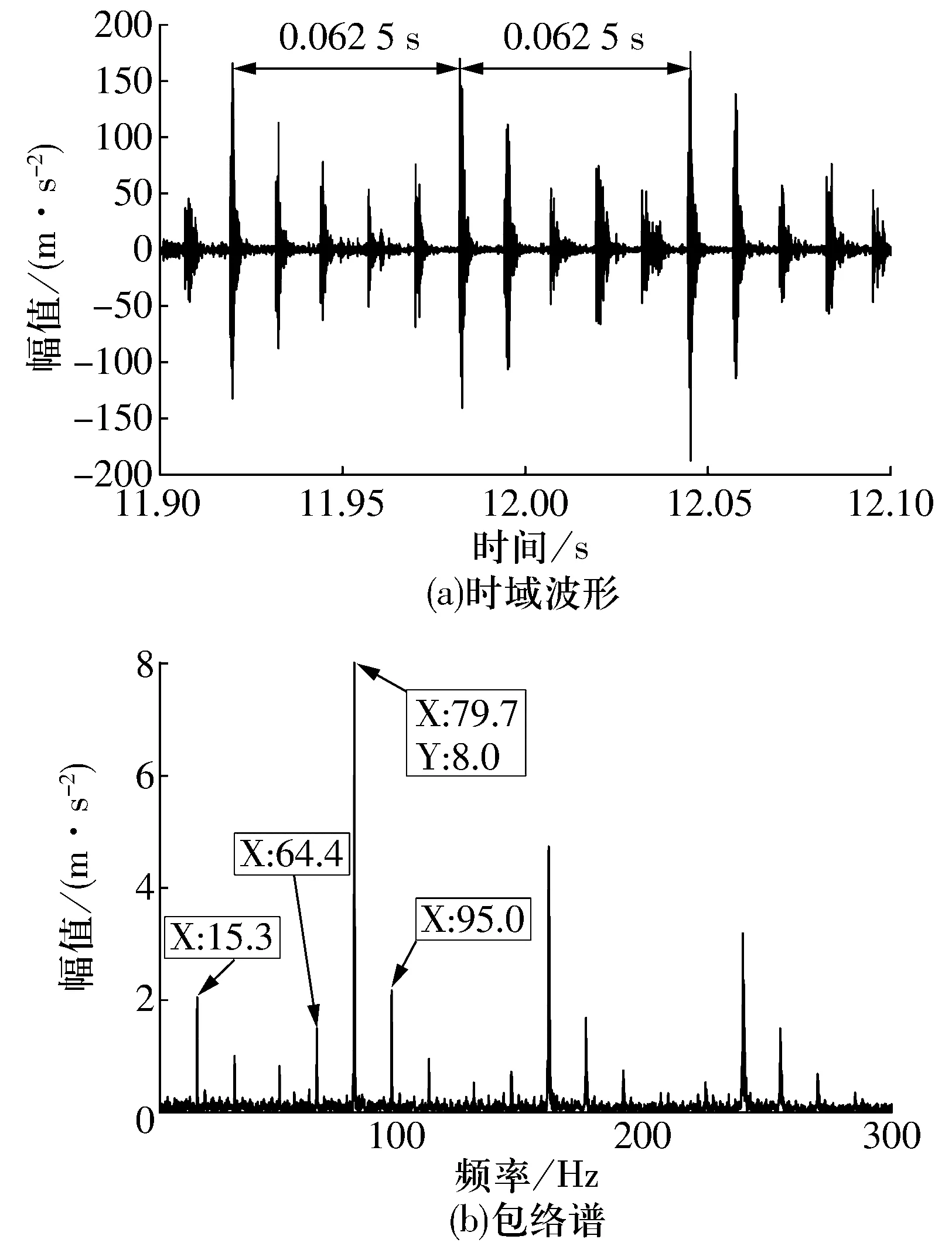
图12 耦合状态下轴承加速度时域波形及包络谱

6 结论

在转子不平衡与外圈缺陷耦合故障状态下轴承力学分析的基础上，提出一种转子-轴承系统动态接触有限元模拟方法，通过分析转子不平衡与轴承外圈缺陷故障耦合状态下的轴承振动加速度和转子轴心轨迹，阐释了故障耦合状态下故障的作用机理，得到以下结论：

1)与轴承外圈故障相比，耦合状态下时域波形中的冲击幅值随转频变化，包络谱中不仅存在转子不平衡与外圈故障的单一故障特征，且外圈通过频率两侧存在差值为转频的边频带。

2)耦合状态下加速度时域波形中冲击幅值主要在滚子出缺陷阶段产生。

3)耦合状态下受载滚子数突变是引起转子轴心轨迹在受载区内出现突变的主要原因。