圆锥滚子轴承滚道参数与振动的灰关联及优化分析

庞晓旭，何青竹，杨丹峰，李梦凯，陈立海

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.洛阳轴承研究所有限公司，河南 洛阳 471039；3.河南省高性能轴承技术重点实验室，河南 洛阳 471039)

轴承素有工业的“关节”之称，广泛应用于国民经济和国防事业等各个领域，是关键的机械基础件之一，其性能直接影响设备的可靠性。轴承振动是综合评价轴承性能的关键指标之一，振动产生的机理非常复杂，涉及轴承制造误差、润滑特性、结构参数以及工况参数等诸多因素，一般通过改善轴承制造工艺，控制套圈的圆度、表面粗糙度及波纹度等误差来减小轴承的振动。

文献[1]分析了轴承滚道直径和滚子直径对轴承振动的影响，结果表明滚子直径对轴承径向振动影响最大，外圈滚道直径次之，内圈滚道直径最小。文献[2]研究了沟曲率半径系数、初始接触角对轴承振动的影响，结果表明存在最优的内外沟曲率半径系数和初始接触角使轴承振动最小。文献[3-6]分析了波纹度对轴承振动的影响，波纹度越大，轴承振动值越大。文献[7]对比分析了角接触轴承的仿真频率成分和试验测试频率成分，结果表明各阶次微振动的幅值主要取决于轴承滚动面的几何误差和预紧力的大小等因素。文献[8]采用极差方法分析了角接触球轴承内外圈沟道参数对轴承振动的影响，结果表明影响轴承振动的程度从大到小依次为外圈沟道表面粗糙度、外圈沟道波纹度、内圈沟道表面粗糙度、外圈沟道圆度、内圈沟道波纹度和外圈沟道圆度。文献[9]分析了轴承内外圈圆度、波纹度和表面粗糙度对轴承振动的影响，结果表明内圈滚道圆度对轴承振动的影响最大。文献[10]分析了内圈大挡边对轴承振动的影响，结果表明内圈大挡边表面粗糙度对轴承振动的影响不大。文献[11]采用灰关联方法分析了影响圆锥滚子轴承振动的因素，得到影响因素重要程度的排序。

本文基于灰色关联度，研究32210圆锥滚子轴承内、外圈滚道的圆度、波纹度和表面粗糙度对轴承振动的影响程度，依据定性融合方法对结果进行了分析和融合，并以此为基础利用响应曲面法建立了轴承振动回归分析模型，得出使轴承振动值达到最小时，各参数间的相对最佳组合。

1 灰关联分析

灰关联分析[12]是根据数据序列之间的距离与几何形状的相似性来评判数据序列之间的关联性。轴承结构参数对轴承振动的影响规律比较复杂，要进行大量的试验才能获得轴承振动的概率分布，进行统计学上的定量分析。灰色系统理论对样本的概率分布无严格要求，且对样本容量也无特别要求。本文采用灰色绝对关联度、灰色相对关联度和灰色综合关联度来分析圆锥滚子轴承滚道参数与振动之间的关联程度，然后采用定性融合方法对各因素进行对比分析。

以轴承滚道参数Xi和轴承振动值Y0(表1)为研究对象，表中“均”字代表1套轴承上3个测点位置的振动平均值。

表1 32210圆锥滚子轴承滚道参数及符号含义Tab.1 Raceway parameters and symbol meanings of 32210 tapered roller bearing

1.1 灰色绝对关联度

灰色绝对关联度依据因素之间的时间序列接近程度判定。对于离散数据列，接近程度指两时间序列在对应时段上曲线斜率的接近程度。若两曲线在各时段上斜率相等或相差较小，则二者的关联系数就大，反之就小。

1)构造序列

设轴承滚道参数构成的原始比较序列为

Xi=(xi(1),xi(2),…,xi(k))，

(1)

轴承振动值构成的原始参考序列为

Y0=(y0(1),y0(2),…,y0(k))，

(2)

式中：i为数据序列号；k为数据序号，k=1,2,…,n。

2)初始化

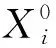
(3)

(4)

(5)

(6)

3)计算灰色绝对关联度

(7)

(8)

(9)

|si-s0|=

(10)

1.2 灰色相对关联度

1)初始化

对(1)，(2)式原始数据进行初始化处理可得

(11)

(12)

(13)

(14)

2)计算灰色相对关联度

(15)

(16)

(17)

(18)

1.3 灰色综合关联度

灰色综合关联度为

(19)

式中：θ为权数。

由(1)—(19)式可知，灰色综合关联度既反映了序列Y0与Xi的相似程度，又可体现出Y0与Xi相当于起始点的变化速率的一致性程度，因此，灰色综合关联度可较为全面综合地反映两数据序列之间联系的紧密程度。一般情况下θ=0.5，但如果较重视绝对量之间的关系，θ值可取稍微大一些；如果较重视序列之间变化的速度关系，θ值也可取小一些。

1.4 灰关联序

为便于叙述比较序列Xi与参考序列Y0之间的灰关联性，定义Xi和Y0的灰关联序列Γ为

Γ=(γ10,γ20,…,γi0,…,γm0)。

(20)

然后将Γ中数据从大到小排序，即为灰关联序。在灰关联序中灰关联度γi0值越大，γi0的排序越靠左，表明Xi与Y0之间的相似程度越大，关联性越强；否则，相似程度越小，关联性越弱。

显然，因为灰关联分析的是相对关系，故单独看γi0值的大小并没有任何意义，因此，研究重点是由各个灰关联度构成的灰关联序列。

2 试验数据分析

2.1 试验数据

以32210圆锥滚子轴承为对象，分别对50套轴承内外圈滚道进行表面粗糙度、波纹度、圆度以及整体振动值进行测试，结果如图1所示，其中k代表第k个套圈。

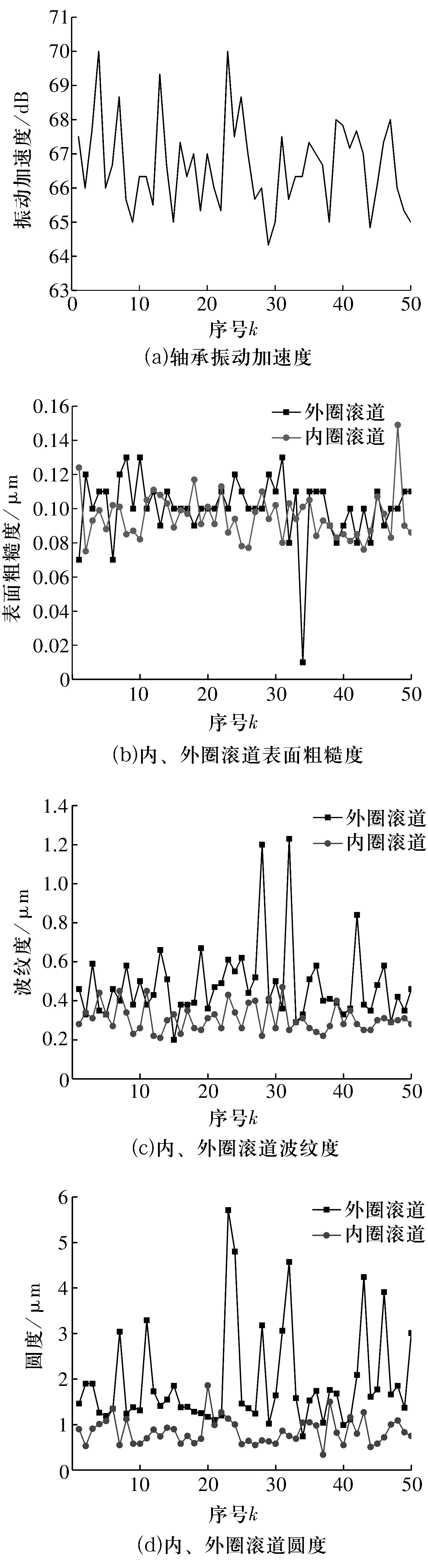
图1 32210圆锥滚子轴承振动和滚道参数试验数据Fig.1 Test data of vibration and raceway parameters of 32210 tapered roller bearing

对轴承振动和滚道参数试验数据进行处理，得到的结果见表2和图2。由表2和图2可知其灰关联序分别为：

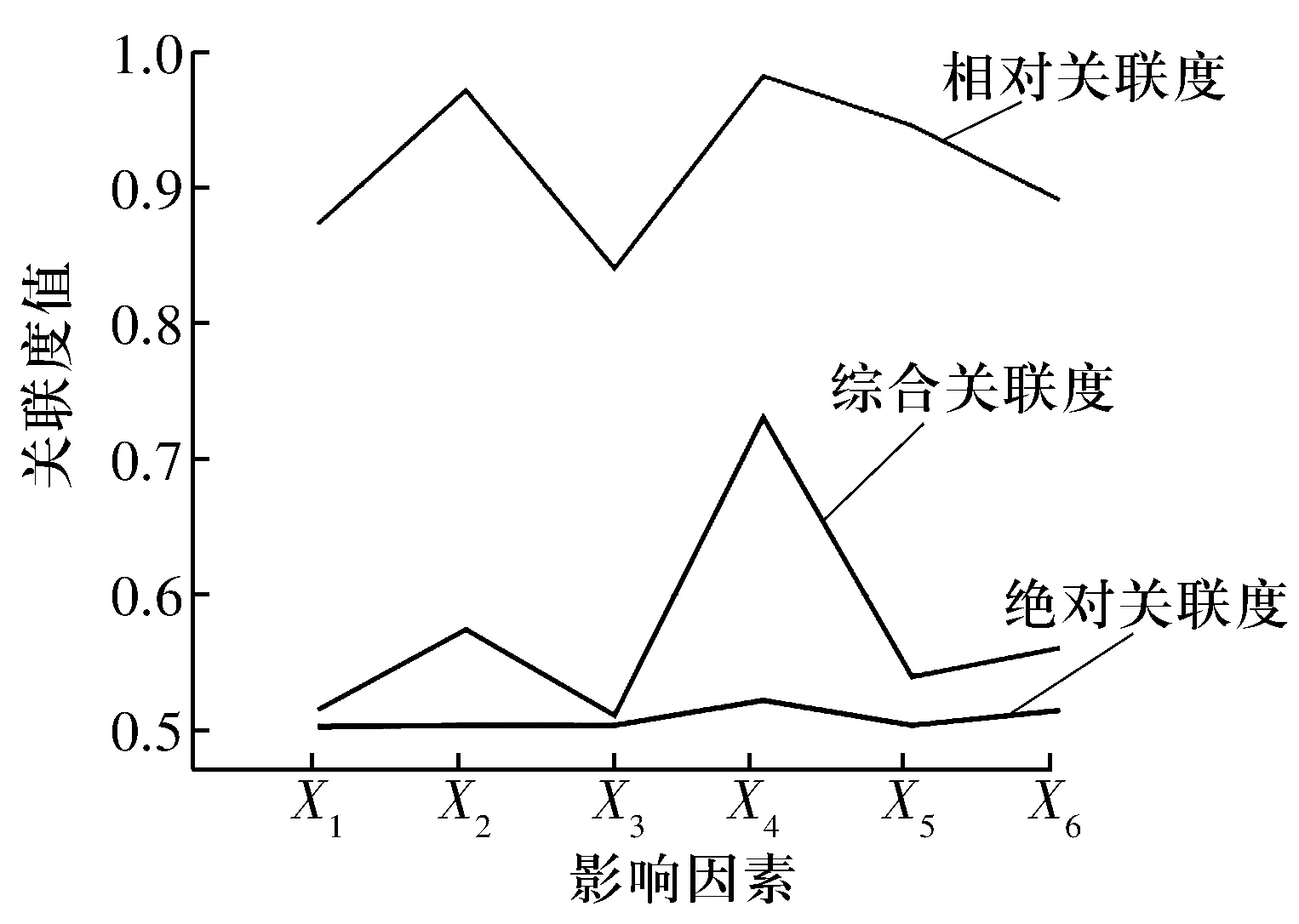
图2 32210圆锥滚子轴承各影响因素的3种灰色关联度Fig.2 Three kinds of grey correlation degree of influencing factors of 32210 tapered roller bearing

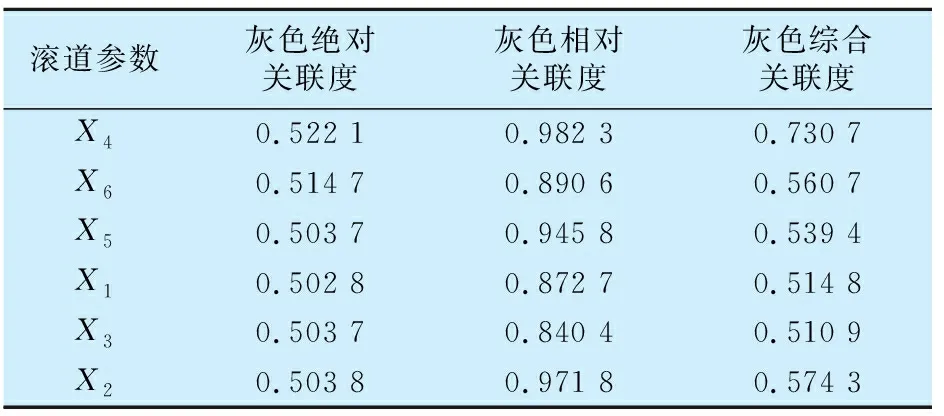
表2 32210圆锥滚子轴承滚道参数与轴承振动的灰色关联度Tab.2 Grey correlation degree between raceway parameters and vibration of 32210 tapered roller bearing

1)灰色绝对关联序

(21)

圆锥滚子轴承滚道各参数对轴承振动值影响程度从大到小依次为：内圈滚道圆度、内圈滚道表面粗糙度、外圈滚道波纹度、外圈滚道表面粗糙度、内圈滚道波纹度和外圈滚道圆度。

2)灰色相对关联序

(22)

圆锥滚子轴承滚道各参数对轴承振动值影响程度从大到小依次为：内圈滚道圆度、外圈滚道波纹度、内圈滚道波纹度、内圈滚道表面粗糙度、外圈滚道圆度和外圈滚道表面粗糙度。

3)灰色综合关联序

Γ=(γ40,γ20,γ60,γ50,γ10,γ30)，

(23)

圆锥滚子轴承滚道各参数对轴承振动值影响程度从大到小依次为：内圈滚道圆度、外圈滚道波纹度、内圈滚道表面粗糙度、内圈滚道波纹度、外圈滚道圆度和外圈滚道表面粗糙度。

2.2 定性融合

由上述3种灰色关联序分析可知，采用不同的灰关联方法得到的结果存在一定偏差，这主要是由于系统信息不完备，数据少，故用不同的分析方法很有可能得出的结果并不相同，甚至可能会彼此矛盾。本文利用定性融合方法对这些结果进行对比分析，将用不同的数学分析方法得到的结果看成解的集合，在某种特定的准则下，从解集中提取具有某种一致性元素的子集，作为最终解。

将由灰色绝对关联度法、灰色相对关联度法和灰色综合关联度法得到的灰关联序中的前4个参数挑出，用参数符号Xi列于表3中。

由表3计算得到各影响参数出现的频数见表4。由表4 可知，内圈滚道各项参数对轴承振动加速度测量值影响要大于外圈滚道各项参数。在轴承实际生产制造过程中，可以通过控制这些对圆锥滚子轴承振动加速度影响较大的参数来降低轴承振动值，进而提高经济效益。

表3 3种计算方法结果的前4个参数Tab.3 The first four parameters of results obtained by three calculation methods

表4 影响参数在3种计算结果中出现的频数Tab.4 Frequency of influencing parameters in three calculation results

3 基于响应曲面法的参数优化

上述分析得到了轴承滚道参数对轴承振动的影响程度，本文将采用响应曲面法研究轴承振动最小的参数组合方式。

3.1 模型的建立与检验

利用Design Expert 10.0.7得出的拟合响应值Y0与因素Xi关系的二项式回归方程为

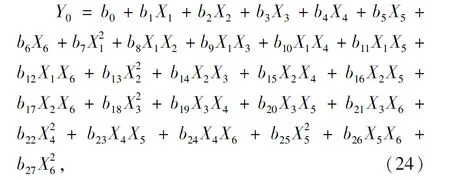
式中：bi为回归系数。

由表3和表4 可知，影响轴承振动值最主要的因素集合为f=(X4,X6)。

由上述分析可知，对轴承振动影响程度最大的是内圈滚道圆度和内圈滚道表面粗糙度，回归系数i=0,1,…,27。则拟合后的参数为b0=61.837,b1=-1.192,b2=36.304,b3=169.786,b4=-0.168,b5=-33.008,b6=-98.064,b7=-1.562,b8=23.429,b9=-0.701,b10=1.906,b11=-28.367,b12=-74.941,b13=-0.266,b14=-55.337,b15=-3.452,b16=3.350,b17=-176.426,b18=-455.181,b19=20.701,b20=-38.107,b21=269.380，b22=0.122，b23=-12.343，b24=-533.549，b25=-0.627，b26=52.741，b27=651.891。

对轴承振动值以及表2中的6个影响因素进行ANOVA方差分析，模型的F值为3.973(F为整个拟合过程的显著性)，P<0.0001(P为不拒绝原假设的性质)，表明该模型在99%置信水平上显著。

轴承振动的实际值与模型预测值的对比如图3所示，这些点较紧凑，且大致分布在y=x这条直线上。对试验值和响应预测值进行拟合，其相关系数r=0.673，而采用此方法进行六元一次，五元二次和四元二次回归分析，其拟合相关系数分别为0.356，0.650，0.612，由此可见，六元二次回归分析模型回归拟合效果相对较好，模型相对具有较高的可信度。

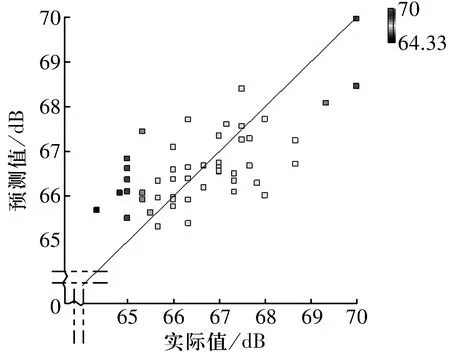
图3 32210圆锥滚子轴承振动实际值与预测值对比Fig.3 Comparison between actual value and predicted value of 32210 tapered roller bearing vibration

为确保模型预测值足够接近试验真实值，故需对模型进行充分性验证。轴承振动值的残差如图4所示。图4a中回归方程所得到的残差在中心线附近随机波动，表明残差之间没有任何相关性；图4b的数据点分布在一条带形区域内，随机分布且无规律；图4c中的数据分布接近在一条直线上，这表明所得到的残差服从正态分布。因此，该模型的残差正态检验良好，残差服从正态分布，说明该模型的误差主要来自于系统的随机误差，并且在可控制的范围之内。

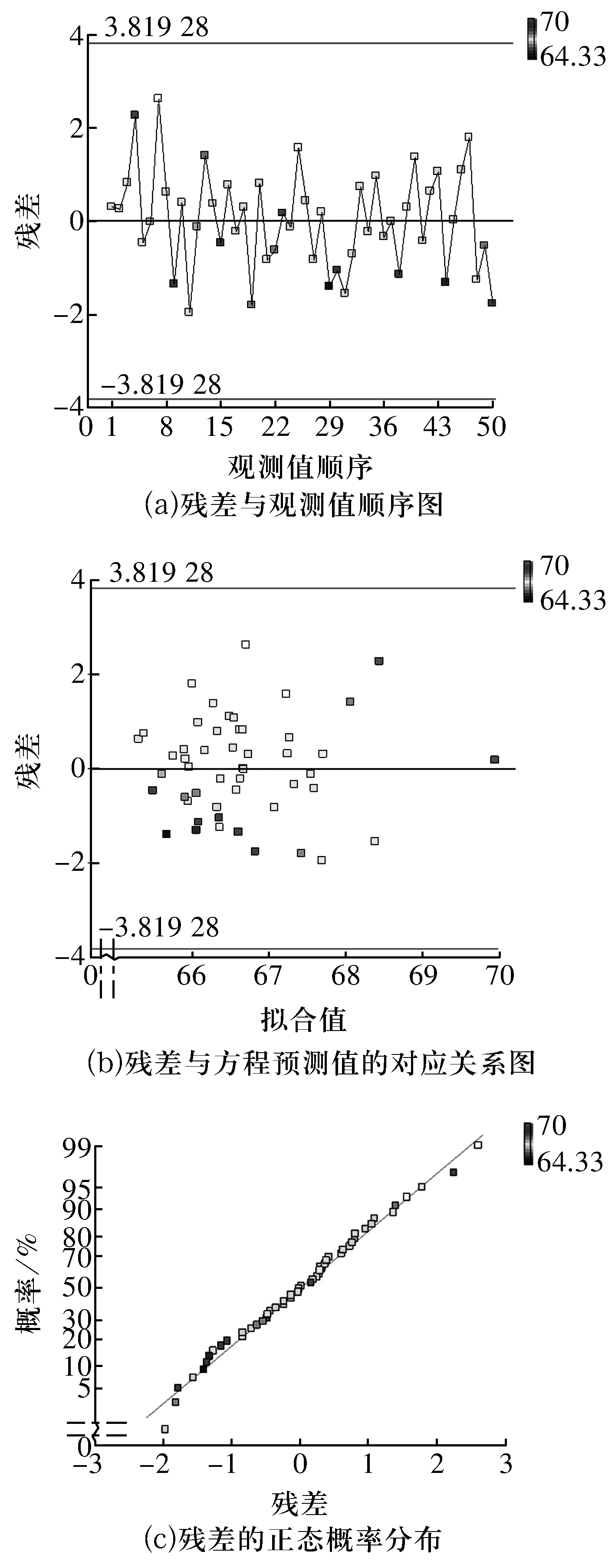
图4 32210圆锥滚子轴承振动响应模型残差Fig.4 Residual error of 32210 tapered roller bearing vibration response model

通过方差分析认为该模型合理，模型的预测值逼近试验真实值，故可有效地表达轴承振动加速度与影响因素之间的关系，作为轴承振动加速度值的试验预测模型。

3.2 参数最佳组合方式

利用Design Expert 10.0.7软件的Numerical模块对所得到的回归方程模型进行响应曲面分析，使内外圈滚道的圆度、波纹度、表面粗糙度值都设定在试验范围之内，求出轴承振动值的最小值(条件设为minimize)。

通过计算得到轴承振动值的最佳参数组合方式，内外圈滚道的圆度、波纹度、表面粗糙度6个因子的优化结果如图5所示,图中斜线代表振动值随自变量变化的规律。由图可知，当外圈滚道圆度、波纹度、表面粗糙度分别为5.710，0.200，

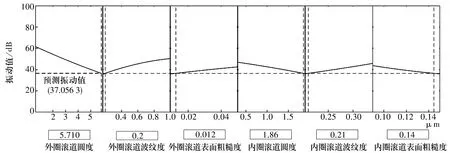
图5 32210圆锥滚子轴承滚道的响应变量优化Fig.5 Optimization of response variables of raceway of 32210 tapered roller bearing

0.012 μm，内圈滚道圆度、波纹度、表面粗糙度分别为1.86，0.21，0.14 μm时，滚动轴承振动值达到最小期望值37 dB，轴承振动最小。

4 结论

1)采用多种灰关联度方法对比分析了32210圆锥滚子轴承内外圈滚道参数对振动的影响程度，得到内圈滚道圆度和内圈滚道表面粗糙度与轴承振动的关联程度大于外圈滚道波纹度、外圈滚道表面粗糙度和内圈滚道波纹度与轴承振动的关联程度，且内圈滚道各项参数对轴承振动值影响要大于外圈滚道各项参数。因此在轴承生产制造过程中，应尽量控制内圈滚道的参数来降低轴承的振动。

2)采用响应曲面法建立了滚道参数与轴承振动间的回归模型，在验证模型正确性的基础上，优化了轴承滚道参数的组合方式，使轴承振动值降低为37 dB。