磁气混合轴承的结构设计与支承特性分析
2021-07-22吴华春黄一鸣张丽胡业发
吴华春,黄一鸣,张丽,胡业发
(1.武汉理工大学 机电工程学院,武汉 430070;2.湖北省磁悬浮工程技术研究中心,武汉 430070)
磁悬浮轴承是一种利用电磁力吸引转子,从而使转子悬浮的一种无接触、无污染、无润滑以及长寿命的高性能轴承[1];箔片气体轴承是一种气体动压轴承,利用弹性箔片作为支承表面,通过转子高速旋转将气体带入由转子偏心形成的楔形缝隙中,从而形成气膜并产生压力使转子悬浮[2],为一种无接触、无润滑、无污染的高性能轴承:两者均为高速旋转机械的支承轴承[3]。箔片轴承虽然结构简单,但在起飞前箔片与轴颈接触会导致转子和箔片磨损,且无法主动调节动态特性。由于材料磁饱和强度限制,磁悬浮轴承结构尺寸较大,需要保护轴承。为此,利用磁悬浮轴承主动可控的特性,结合箔片轴承提供高速保护,形成一种新式磁气混合轴承,其优势在于[4]:降低箔片轴承起飞前的摩擦损耗,改善转子的动态性能,提高承载能力,且可省去磁悬浮轴承的保护轴承。
有许多学者针对磁气混合轴承进行了相关研究。文献[5]针对磁气混合轴承中电磁轴承工作在偏心位置下的电磁力非线性化进行了相关研究,并提出一种理论计算方法计算给定载荷分配系数和预定运行状态下磁气混合轴承的承载力、动态刚度和动态阻尼。文献[6]为简化磁气混合轴承控制器设计,提高系统的性能,提出一种磁气混合轴承自适应控制方法:首先,利用特征建模方法建立了磁气混合轴承的集中二阶模型, 通过实时参数辨识得到模型参数;然后,采用黄金分割控制器适应箔片轴承的参数变化,保证闭环系统的稳定性;最后,通过数值模拟验证了该方法的有效性。文献[7]搭建了一个由磁气混合轴承支承的刚性转子,使其在1.8×104r/min的速度下运行,并使用PD控制算法降低振动幅度;为阐明转子初始偏心位置的影响,控制算法从转子的初始位置开始使用恒定增益值,结果表明当磁气混合轴承工作时,电磁力对抑制磁气混合轴承支承的转子的次同步振动有显著效果,且当偏心率为0.2~0.5时箔片轴承的载荷分布最优。
目前,磁气混合轴承的相关研究集中在试验和控制,其中针对结构和支承特性的研究也多从箔片轴承入手。因此,本文主要研究磁气混合轴承的结构和支承特性,利用Simulink建立磁气混合轴承的仿真模型,从磁悬浮轴承的角度分析控制电流、支承力等参数与偏心率的关系。
1 磁气混合轴承结构
1.1 磁悬浮轴承的结构
8极径向主动磁悬浮轴承结构简单,加工方便,与箔片轴承互补性更好且易于控制[8],所以选其作为磁气混合轴承中的磁悬浮轴承,其结构如图1所示。磁极分布采用NNSSNNSS的形式,磁极间耦合较少,易于控制,并且磁极对采用45°偏置放置,可提高磁悬浮轴承的承载能力。

1—轴;2—定子;3—线圈;4—转子
1.2 箔片轴承结构
选用整周式带底箔的箔片轴承,其结构如图2所示,底箔提供弹性支承,顶箔提供完整的圆周表面并直接与转子内表面接触。工作原理是通过转子高速旋转将气体带入由转子偏心形成的楔形缝隙中,从而形成气膜,产生压力使转子悬浮[2]。
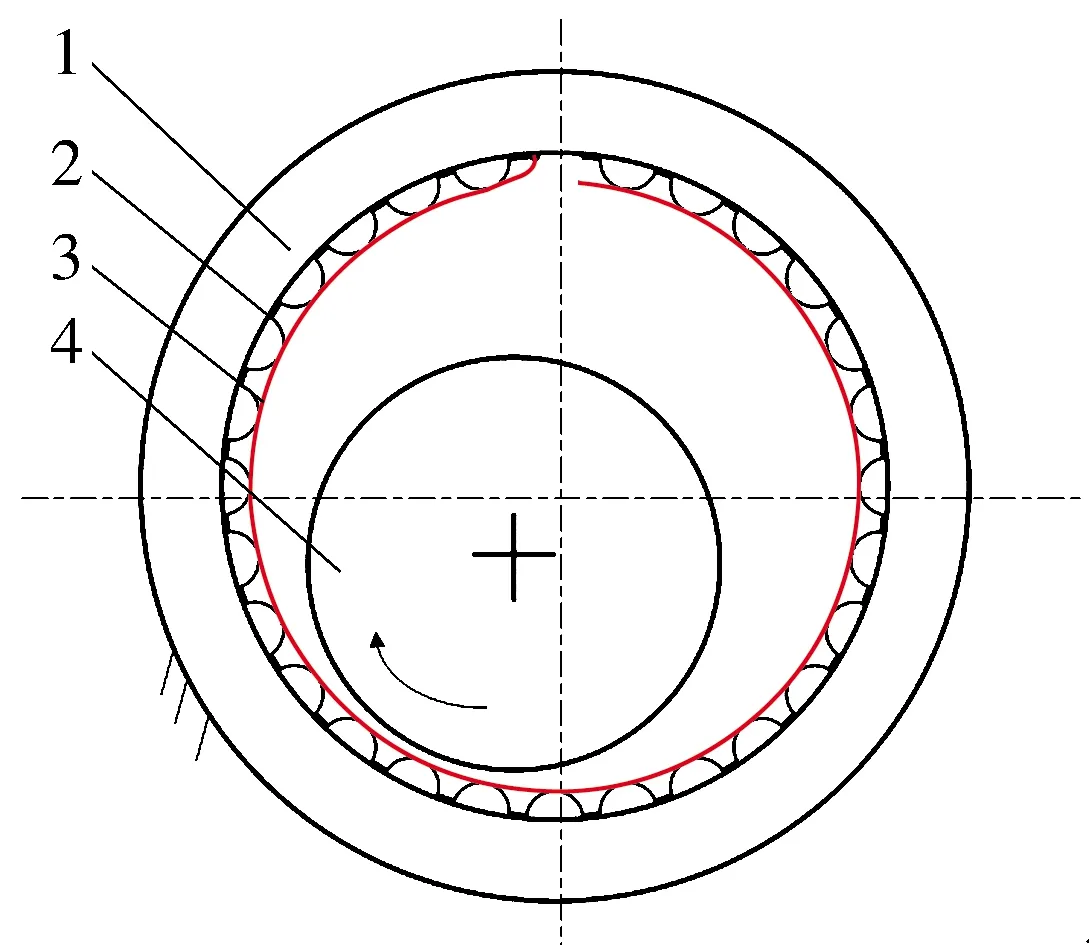
1—轴承座;2—底箔;3—顶箔;4—转子
箔片轴承主要是针对图3中的底箔拱距、拱高、支承拱弦长、顶箔和底箔厚度等箔片的结构参数进行设计。

图3 箔片轴承结构参数Fig.3 Structure parameters of foil bearing
因箔片轴承起飞前箔片直接接触转子,所以箔片轴承需要选取耐高温、高弹性的镍基合金材料。为增加箔片轴承的耐磨性,需在顶箔与转子接触面上涂耐磨层,例如PS304粉末等[9]。
1.3 磁气混合轴承结构
目前磁气混合轴承主要有2种结构排布方式:1)将磁悬浮轴承和箔片轴承并列布置在轴颈上,如图4所示,FM为磁悬浮轴承承载力,Ff为箔片轴承承载力,G为转子重力;2)将箔片轴承嵌入磁悬浮定子与转子的气隙之间,箔片固定于磁悬浮极间插入的支座上,如图5所示。

图4 并联式磁气混合轴承结构示意图Fig.4 Structure diagram of parallel hybrid magnetic-foil bearing

1—磁悬浮轴承;2—箔片轴承;3—支座;4—转轴
第1种结构简单,磁悬浮轴承和箔片轴承的耦合性较弱,易于控制,但增加了轴向长度;第2种结构紧凑,磁气耦合性较强,控制效果好,但结构复杂,控制难度较大。本文选用第1种磁气混合轴承结构进行研究。
2 磁气混合轴承建模
2.1 磁悬浮轴承承载力
磁悬浮轴承通常采用差动控制,其结构原理如图6所示。差动控制优点是可以产生正向和反向的作用力,且动态响应更好[1]。

图6 磁悬浮轴承差动控制原理Fig.6 Differential control principle of magnetic bearing
当采用差动控制时,上端电磁铁产生的电磁力为F1,下端电磁铁产生的电磁力为F2,气隙为x0,偏置电流为i0,控制电流为ix,x为转子竖直方向位移,n为线圈匝数,α为极间夹角的一半。根据麦克斯韦吸引力公式得到两者的合力,即磁悬浮轴承承载力FM为[10]
FM=F1-F2=
(1)
k=μ0A0n2,
(2)
式中:μ0为真空磁导率;A0为磁悬浮轴承定子的磁极面积。
对(1)式在(ix=i0,x=0)的领域进行泰勒展开,且忽略高阶项,有
(3)
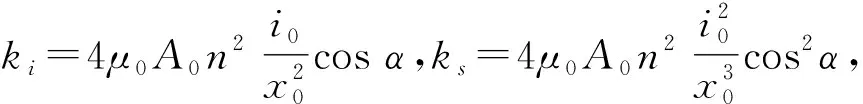
FM=kiix+ksx,
(4)
式中:ki为磁悬浮轴承的力-电流刚度系数;ks为力-位移刚度系数。虽然(4)式在转子偏移量较大时精度会下降,但箔片轴承的半径间隙一般为0.02~0.05 mm[2],相较于磁悬浮轴承的气隙来说较小,所以,小偏心率下的磁气混合轴承可使用(4)式进行研究。
2.2 箔片轴承承载力
通常采用气弹耦合求解法研究箔片轴承的稳态特性[11-12]。在小扰动情况下将箔片变形方程与气体动压润滑雷诺方程联立迭代求解出间隙的动态压力分布,再积分求解出箔片轴承的动态刚度和动态阻尼系数等相关参数。
现采用相关经验公式来求解箔片轴承承载力Ff[2], 即
(5)
式中:μ为气体动力黏度;R为箔片轴承的轴颈半径;Ω为轴颈工作角速度;L为箔片轴承长度;C0为名义间隙;ε为转子偏心率,即偏心距与名义间隙之比。(5)式一般适合长径比小于0.5,且偏心率小于0.75的情况。
2.3 磁气混合轴承数学模型
当磁悬浮轴承与箔片轴承的间距很小时,两者的作用力近似看成作用于一点。先对磁气混合轴承的单自由度进行分析。其结构和受力如图4所示。
根据运动学方程可得
(6)

(7)
3 支承特性仿真分析
3.1 Simulink建模
磁悬浮轴承采用PID控制。利用Simulink软件并根据(7)式进行磁气混合轴承建模,模型如图7所示。其他仿真参数见表1。
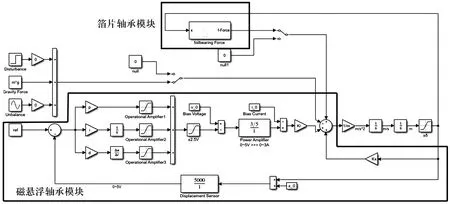
图7 磁气混合轴承Simulink模型Fig.7 Simulink model of hybrid magnetic-foil bearing
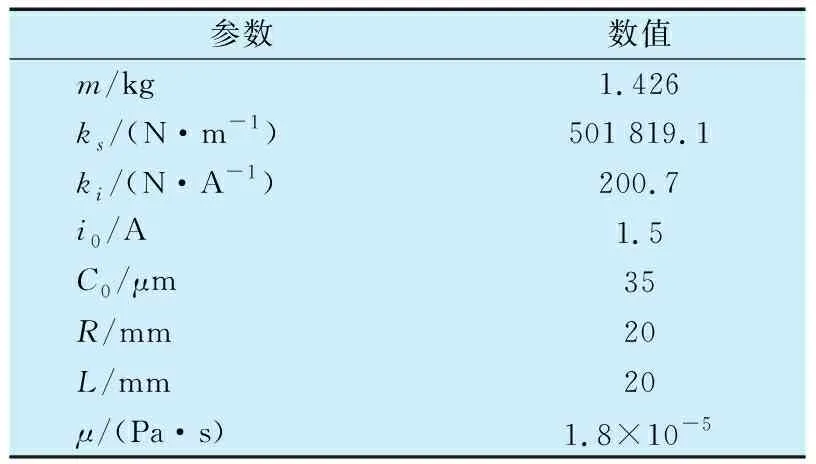
表1 磁气混合轴承模型仿真参数Tab.1 Simulation parameters of magnetic gas hybrid bearing model
3.2 磁悬浮轴承起浮曲线
设置仿真参数后令转速为0,调节PID参数,经PID参数整定得KP=4,KI=50,KD=0.002 3,得到磁悬浮轴承单自由度静态起浮曲线如图8所示,磁悬浮轴承振荡2~3次后,在时间t为0.015 s左右达到稳态,所以此组PID参数具有较好的控制效果。
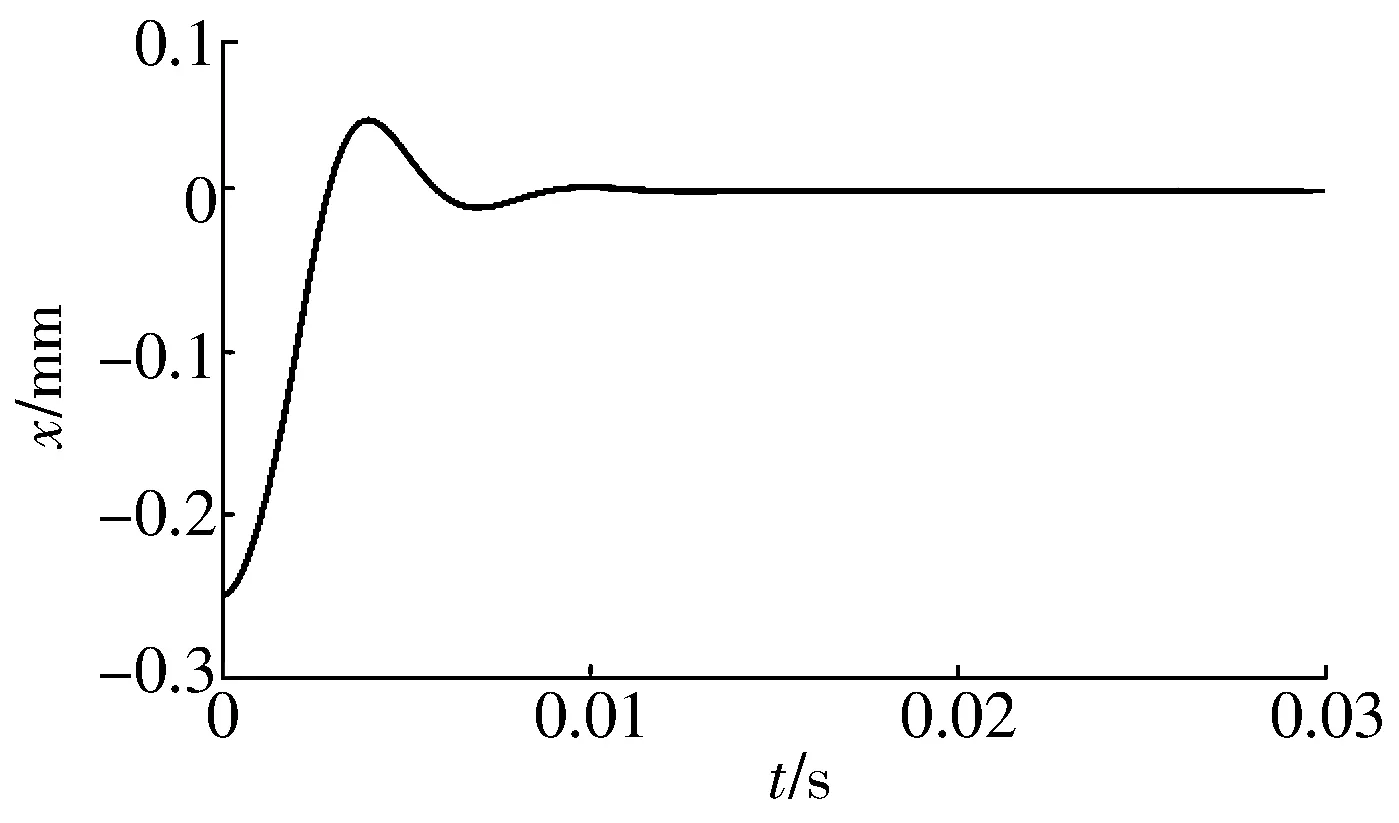
图8 磁悬浮轴承静态起浮曲线Fig.8 Levitation curve of magnetic bearing
3.3 不同偏心率下电流的变化
更改磁悬浮轴承稳态参考位置,使磁悬浮轴承悬浮于偏心状态,此时偏心距为21 μm,换算成箔片轴承的偏心率为0.6。设置10 s后转子由静止开始加速,50 s达到60 000 r/min后保持转速不变,可得到磁悬浮轴承磁极的控制电流i的变化,如图9所示。

图9 转子转速变化和控制电流变化Fig.9 Changes of rotor speed and control current
由图9可知:磁悬浮轴承在静态起浮时,前0.015 s控制电流有波动,随后达到稳态;10 s后转速开始升高,此时箔片轴承的动压力开始加入,承担一部分重力,减小了磁悬浮轴承分担的力,控制电流逐渐减小;达到给定转速后控制电流再次达到稳态;整个过程控制电流从0.113 A降到0.057 A,控制电流降低了49.5%。
同理,研究不同偏心率下控制电流的变化,结果如图10所示,令磁悬浮轴承静态起浮稳定后的控制电流为i0,转速稳定后的控制电流为ir,两者的差为Δi。由图10可知:随着偏心率的增大,i0逐渐增大,而ir逐渐减小,Δi随偏心率的增大而增大。说明随着偏心率的增大,磁悬浮轴承气隙增大,需要更大的电流产生更大的电磁力,以平衡重力。随着转速逐渐升至给定转速,箔片轴承承载力逐渐增大,以分担磁悬浮轴承所承载的重力,从而使控制电流明显减小。所以,箔片轴承能有效降低磁悬浮轴承的控制电流和功耗。

图10 控制电流随偏心率的变化曲线Fig.10 Variation curve of control current with eccentricity
3.4 不同偏心率下的承载力
转速为60 000 r/min时,不同偏心率下磁悬浮轴承和箔片轴承承载力的变化如图11所示(令二者的合力为F):随着偏心率的增大,磁悬浮轴承的承载力逐渐减小,而箔片轴承的承载力逐渐增大。由(6)式可知,稳态时加速度几乎为0,则磁悬浮轴承和箔片轴承的合力F等于重力。
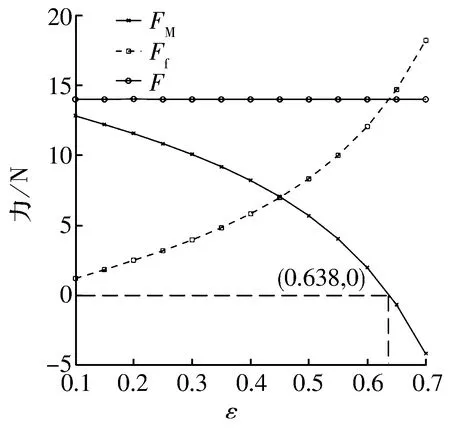
图11 承载力随偏心率的变化曲线Fig.11 Variation curve of bearing force with eccentricity
箔片轴承的加入能有效帮助磁悬浮轴承分担载荷,但不是偏心率越大越好。由图11可知:当偏心率为0.638左右时,磁悬浮轴承承载力为0,继续增大偏心率至0.7时变为负值,说明此时磁悬浮轴承的承载力与重力同向,意味着箔片轴承的承载力过大,磁悬浮轴承需要反向来平衡箔片轴承的承载力,需降低转速或减小偏心率,达到电磁力近似为0的理想工作状态。
4 试验
为验证仿真模型结果,搭建磁气混合轴承测试平台,如图12所示,磁悬浮轴承和箔片轴承并联排布,高速电主轴通过联轴器驱动轴旋转。

图12 磁气混合轴承测试平台Fig.12 Hybrid magnetic-foil bearing test platform
试验平台的工作原理是磁悬浮轴承端盖上的传感器将位移信号传送到dSPACE控制器,控制器将控制信号输送到功率放大器,由功率放大器输出控制电流至磁悬浮轴承。转子起浮曲线如图13所示,静态悬浮时轴心实时位移信号如图14所示,分析可知:磁悬浮轴承于1.5 ms起浮于平衡位置,且静态悬浮时位移在±10 μm以内,悬浮精度较好。
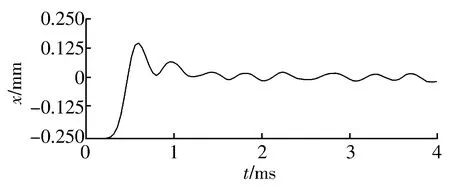
图13 转子起浮曲线Fig.13 Levitation curve of rotor

图14 轴心实时位移信号Fig.14 Real time displacement signal of axis centre
5 结论
针对磁气混合轴承的布置形式、载荷分配及支承特性等问题进行研究,给出磁悬浮轴承和箔片轴承的承载力,以此为基础推导了磁气混合轴承支承单自由度数学模型。利用Simulink软件建立控制仿真模型,对磁气混合轴承的相关特性进行分析,得出以下结论:
1)随着偏心率增大,初始控制电流变大,转速稳定后控制电流明显减小。
2)转速恒定时,随着偏心率增大,磁悬浮轴承的承载力减小,箔片轴承的承载力增大,载荷比减小。
