直驱风力发电机主轴承载荷分布数值分析
2021-07-22李海江王腾飞郭四洲马帅军闫柯
李海江,王腾飞,郭四洲,马帅军,闫柯
(1.中车株洲电机有限公司,湖南 株洲 412000;2.西安交通大学 现代设计及转子轴承系统教育部重点实验室,西安 710049)
1 概述
风能是重要的清洁能源,大规模风能开发与利用是我国重要的能源战略。传统非直驱风力发电机传动链由叶片、轮毂、主轴、齿轮箱和发电机组成,齿轮箱故障会导致风电装备发生安全事故,增加维护成本[1]。近年来,大功率(目前已高达12 MW)直驱风力发电机组已成为我国风电新增容量的主力机型之一[2]。一种典型的直驱风力发电机组传动链示意图如图1所示,发电机组由风轮(叶片+轮毂)直接驱动发电机,发电机转轴(主轴)一般采用空心轴,发电机轴承(直驱风力发电机组主轴承)为2套单列圆锥滚子轴承。直驱风力发电机组传动链中没有齿轮箱,从根本上解决了齿轮箱的安全、维护等重大问题,但强阵风直接冲击在主轴承上,对主轴承性能提出了极高要求。主轴承一般在低速重载工况下工作,准确分析其载荷分布,合理设计和配置主轴承,对于直驱风力发电机组安全运行至关重要。
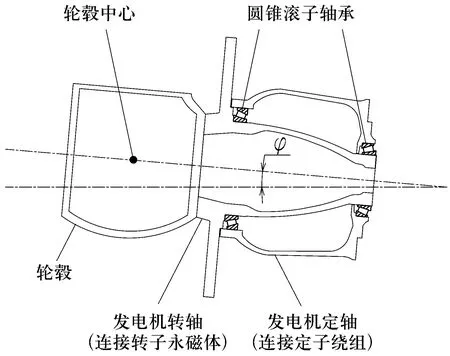
图1 直驱风力发电机组传动链示意图Fig.1 Transmission chain diagram of direct-driven wind turbine
直驱风力发电机主轴承(以下简称主轴承)受力分析是一个复杂的非线性问题,其难点在于既要考虑轴承各个方向刚度之间的耦合性与非线性,又要与主轴的受力相结合进行轴系分析,目前一般采用有限元法[3-4]。采用有限元法分析复杂轴系问题时,轴承主要有4种处理方法:
1)忽略轴承刚度将其简化成支点,或忽略轴承刚度的耦合性和非线性将其简化成线性弹簧,然后进行轴系分析[5]。该方法过于简化,难以反映轴承的真实受力状态。
2)采用全实体有限元模型,通过有限元非线性接触算法求解轴承的受力与变形[6-7]。该方法可以考虑轴承内部结构的影响,计算结果接近真实值,但全实体有限元模型网格数量大,对计算硬件资源要求极高,耗时耗力,且不易收敛。
3)将滚子与滚道的接触简化为非线性弹簧,通过有限元非线性接触算法求解轴承的受力与变形[8]。该方法减少了计算量,但非线性弹簧建模繁琐。
4)在有限元法基础上,考虑轴承刚度耦合性和非线性,建立轴系刚度非线性有限元模型并进行数值求解[8-10]。该方法理论基本完备,模型简化合理,在处理复杂轴系问题时具有更高的计算效率和计算精度。
现有文献鲜有报道考虑轴系刚度非线性的直驱风力发电机主轴承载荷分布有限元分析方法。针对直驱风力发电机主轴承的结构特点,在第4种方法的基础上,提出一种考虑轴承刚度耦合性和非线性的有限元法,推导轴承单元刚度矩阵的解析表达式,采用考虑剪切变形的欧拉-伯努利梁单元建立空心主轴模型,构建直驱风力发电机轴系整体计算模型,采用牛顿-拉夫逊法求解极限风载作用下主轴承的载荷分布,运用自主开发的程序对某非标2TS轴承计算验证。载荷分布计算结果与成熟商业软件结果进行对比,并将所提计算模型的摩擦力矩计算结果与试验结果进行对比。
2 轴承单元与空心轴单元模型
当轴系承受载荷不同时,轴承中受载滚动体数量和所受载荷大小不同,轴承变形与载荷之间存在非线性关系,刚度表现为非线性。轴承各方向刚度之间相互影响,存在耦合关系。以直驱风力发电机中常用的2TS轴承为例推导考虑刚度非线性和耦合性的刚度矩阵表达式。
对于钢制轴承,滚子与套圈滚道的接触载荷为[11]
Q=kδ1.11,
(1)
式中:k为滚子与套圈滚道的接触刚度系数;δ为滚子法向接触变形。
刚度系数的修正公式为[9]
(2)
式中:Lwe为滚子有效长度;αe,αi,αf分别为圆锥滚子与外圈、内圈及挡边的接触角。
在径向载荷Fr、轴向载荷Fa及力矩M联合作用下,圆锥滚子轴承内圈相对于外圈将产生径向位移δr、轴向位移δa和转角θ,如图2所示。
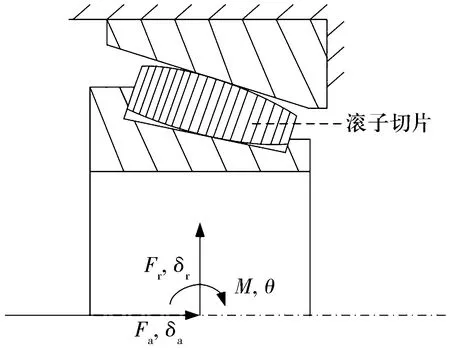
图2 圆锥滚子轴承受力示意图Fig.2 Stress diagram of tapered roller bearing
在位置角ψj处的滚子位移为
δrj=δrcosψj,
(3)
δaj=δa,
(4)
式中:δrj,δaj分别为第j个滚子的径向位移和轴向位移。
转角θ会引起位置角ψj处滚子的轴向位移和径向位移变化,但不会改变总的法向接触变形。由转角θ引起位置角ψj处滚子的轴向位移为
(5)
式中:Dpw为滚子组节圆直径。
滚子总的轴向位移为
(6)
转角θ引起的径向位移较小,可忽略。考虑滚子偏转对接触载荷及变形的影响,将滚子沿长度方向切成m片(图2),可得滚子与滚道接触法线法向变形为
δnj=δajcosα+δbajsinα=
(7)
第j个滚子第i个切片所受的径向力、轴向力分别为
(8)
(9)
第j个滚子第i个切片在轴承中心形成的力矩为
(10)
由于滚子发生偏转,切片产生的附加力矩为
(11)
则第j个滚子第i个切片形成的总力矩为
Mji=Meji+Mθji=
(12)
式中:xi为第i个切片中心的坐标。
根据载荷及力矩平衡关系可得
(13)
(14)
(15)
由(12)—(14)式可得Fr,Fa,M与δr,δa,θ的关系,建立轴承单元刚度方程
F=Kδ,
(16)
其中,位移矢量δ=(δr,δa,θ)T,载荷矢量F=(Fr,Fa,M)T。计算得到轴承刚度矩阵为
(17)
直驱风力发电机主轴一般为变截面空心轴,异形轮毂与主轴相连,为方便编程将其等效为主轴的延伸段,轴单元采用欧拉-伯努利梁单元建模。编制程序时,在主轴上载荷(风载、重力、单边磁拉力)作用位置及轴承位置处设置节点,将轴分为5个轴段,每一段都是一个6×6的梁单元,其单元刚度矩阵表达式见文献[12]。主轴总体刚度矩阵由所有梁单元刚度矩阵组合得到,其单元刚度Ks组合形式为
Ks=
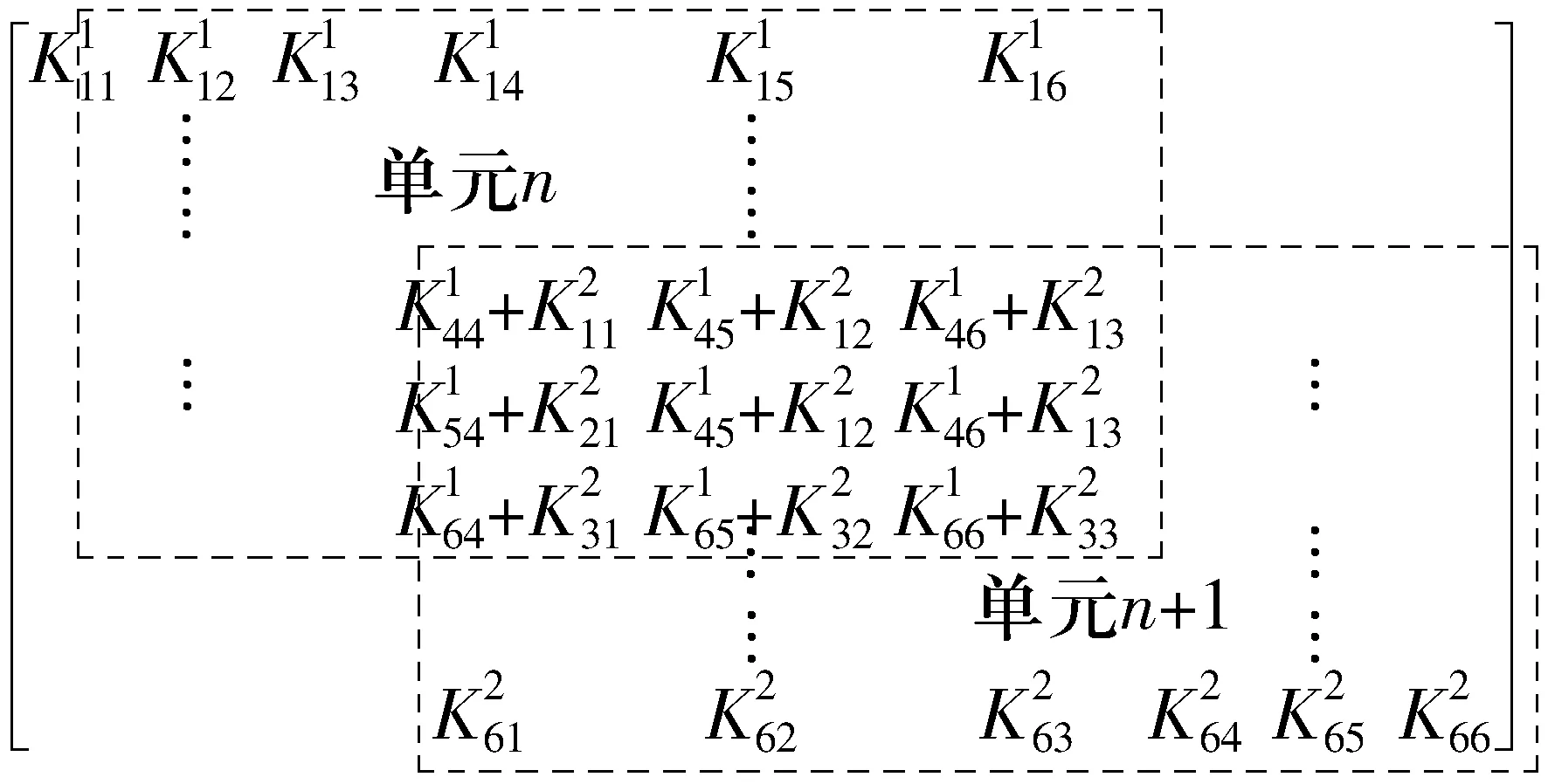
(18)
3 轴承载荷分布数值求解
为计算轴承载荷分布,需要将轴和轴承的刚度矩阵进行组合形成总体刚度矩阵。最终轴承节点的位移和相应轴节点处的位移必须满足变形协调关系,轴承节点产生的力和相应轴节点处产生的力要满足平衡条件。假定安装轴承的2个节点分别为n1和n2,轴承节点刚度矩阵为Kb,轴刚度矩阵为Ks,只需把共节点处的轴刚度矩阵和轴承刚度矩阵叠加即生成系统总体刚度矩阵K,可表示为
K=
(19)
以此建立系统力学平衡方程
P=Kδ,
(20)
式中:P为载荷矢量,即施加于轴系的实际载荷;δ为轴变形量。
可以采用牛顿-拉夫逊法求解该非线性方程组,收敛判据为相邻两次迭代的节点位移或节点力小于给定小量。计算得到的节点位移矢量即为轴上各节点的位移,将轴承所在节点的位移代入轴承载荷计算公式,即可得到各轴承的载荷。将上述过程编制成VB程序,可快速求解轴承载荷分布。
4 模型验证
以某型号直驱风力发电机2TS主轴承为例,轴系模型如图3所示。轴系载荷中心位于图1中的轮毂中心处。为便于计算,将轮毂简化为空心主轴的延长,载荷中心位于图3中空心主轴最左端轴心O处,轴承外圈固定。轴承相关参数见表1。等效载荷Fx=100 kN,Fy=960 kN,Fz=110 kN,My=-10 000 kN·m,Mz=-900 kN·m。内外圈及滚子材料为渗碳钢,其弹性模量为206 GPa,泊松比为0.3。

图3 轴系模型示意图Fig.3 Diagram of shafting model

表1 圆锥滚子轴承基本参数Tab.1 Basic parameters of tapered roller bearing
4.1 载荷分布验证
为验证计算模型的正确性,采用上述方法计算轴承载荷分布,并与成熟商业软件计算结果进行对比。
理论计算及商业软件基于各自的算法与程序,得到的载荷分布如图4所示(滚子0°位置角位于轴承正下方),轴承承载区基本一致,前轴承最大载荷偏差为5.6%,后轴承最大载荷偏差为1%,误差在允许范围内,说明了计算模型的正确性。将最大载荷代入自主开发的圆锥滚子接触分析数值计算程序,即可求得滚子接触应力分布。综合滚子载荷分布与接触应力分布,对照风电行业相关设计标准,可判断主轴承是否能安全运行。

图4 轴承载荷分布Fig.4 Load distribution of bearings
4.2 摩擦力矩验证
轴承摩擦力矩测量示意图如图5所示,发电机竖直安置于平台上,尼龙吊带一端固定在发电机定轴上,另一端固定在叉车上,叉车拖动定轴旋转,测量拉力值,换算得到主轴承摩擦力矩。装配过程对2TS轴承端盖预紧,预紧力取650 kN。测量装配完成后的6台风力发电机轴承摩擦力矩(每台测量10次,取平均值),结果见表2。

图5 主轴承摩擦力矩测量示意图Fig.5 Measuring diagram of friction torque of main bearing

表2 摩擦力矩测量值Tab.2 Measured values of friction torque
由表2可知:摩擦力矩测量值在4 176~4 680 N·m范围内,最大值与最小值之间的相对误差为10.8%。摩擦力矩测量值波动是轴承润滑状态、密封状态、旋转精度等因素共同影响的结果,此外,使用叉车测量大尺寸电机轴承的摩擦力矩,在实际操作上也会带来一定误差。
采用经验公式计算2TS主轴承的理论摩擦力矩[13]
(21)
式中:μ为摩擦因数;d为摩擦力作用内径;P为轴承当量动载荷。
用提出的模型计算得到试验条件下主轴承的等效静载荷见表3,参考ISO 281:2007 Rolling bearings—dynamic load ratings and rating life,可由等效静载荷计算得到当量动载荷P,由(21)式计算出M。

表3 轴承载荷计算结果Tab.3 Load calculation results of bearings
(21)式中摩擦因数μ与轴承运行、承载、润滑、密封状态等因素有关,目前难以精确测定,文献[14]给出了摩擦因数取值范围为0.001 8~0.002 8,将其代入(21)式可得前后轴承摩擦力,进而得到总摩擦力矩M总=M前+M后=3 817~5 938 N·m。摩擦力矩实测值在4 176~4 680 N·m范围内波动,包含在计算值3 817~5 938 N·m范围内,说明了计算模型的正确性。
由于(21)式中摩擦因数μ取值波动较大,最大值与最小值之间的相对误差达27.4%,也造成摩擦力矩计算值相对误差较大,而在表2中,摩擦力矩测量值相对误差仅10.8%。今后需进一步研究摩擦因数μ的取值范围,从而更好地验证计算模型的准确性。
5 结束语
针对直驱风力发电机主轴承建立了一种考虑轴承刚度非线性和耦合性的轴承单元,推导了轴承刚度矩阵的解析表达式。针对直驱风力发电机变截面空心主轴建立了梁单元主轴模型,将轴承与主轴模型组合得到直驱风力发电机轴系有限元计算模型,并采用牛顿-拉夫逊法进行求解。通过与商用软件计算结果及现场测试结果对比,证实了提出的模型能够有效计算给定外载荷下直驱风力发电机主轴承的载荷分布,已成功应用于直驱风力发电机的开发设计。
