滚动关节轴承摩擦力矩检测装置设计及运动分析

季晔，宗晓明，高飞，权思佳，卢阳

(1.洛阳理工学院，河南 洛阳 471023；2.中航光电科技股份有限公司，河南 洛阳 471003；3.洛阳轴承研究所有限公司，河南 洛阳 471039；4.河南科技大学，河南 洛阳 471003；5.高端轴承摩擦学技术与应用国家地方联合工程实验室，河南 洛阳 471003)

摩擦力矩是评价和影响轴承质量的重要参数，摩擦对轴承性能研究的重要性日益得到重视，摩擦学也成为轴承研发的基础理论，各国学者在Palmgren[1]轴承摩擦力矩计算公式的基础上开展了大量研究[2-3]。文献[4]研究了角接触球轴承沟曲率半径系数对摩擦力矩的影响；文献[5]建立了推力球轴承动力学模型和摩擦力矩数学模型，得到了不同工况对轴承摩擦力矩的影响。近些年，国外学者研究了轴承摩擦力矩与润滑油性质、温度、载荷等因素之间的关系，研制了针对性的轴承摩擦力矩测量系统[6]。文献[7]基于传递测量法研制了带密闭容腔的轴承摩擦力矩测试仪；文献[8]研制了双杠杆式轴承摩擦力矩测量系统；文献[9]研制了M992微型轴承转动摩擦力矩测量仪；文献[10]设计了圆锥滚子轴承摩擦力矩测量仪。

滚动关节轴承主要用于精密机械，要求具备零间隙、高运动精度、高刚度和低阻尼等特点，与之配套的摩擦力矩等性能参数测量装置在国内未见报道，有必要进行相关研究。根据滚动关节轴承的运动特点，其摩擦力矩测量仪器需具备3个独立的空间转动自由度，可以采用并联机构实现[11-13]。文献[14]研究了3-PSU&S三转动自由度并联机构的运动学设计问题，分析了闭环矢量法建立机构位置逆解模型，推导出关节空间与操作空间的速度映射模型；文献[15]以一种三转动自由度数控台为对象,研究了该机构的奇异位形、工作空间及尺度综合；文献[16-17]对三转动并联机构进行了结构类型综合，设计了一种能辅助实现人体踝关节运动的三转动并联机构，并对其进行了运动学分析；文献[18]基于G_F集理论提出了一种具有三转动运动特征的四支链并联机构构型方法。

综上分析，本文设计了一种用于滚动关节轴承摩擦力矩测量的混联机构。针对测量装置的核心单元——三转动并联机构，利用螺旋理论分析了机构运动原理，建立机构输入、输出关系方程并推导出输入、输出运动学关系表达式。给定尺度参数，分析了运动平台工作空间、位置正解方法，并根据某一摩擦力矩检测路径得到了机构运动学参数变化规律。

1 滚动关节轴承结构

如图1所示，滚动关节轴承由推力杆、轴承座、滚动体和保持架组成。轴承座上有4个用于连接固定的螺栓孔，推力杆末端通过外螺纹与其他杆件相连，另一端为球头，安放于保持架内。目前，该类轴承主要由日本企业生产，国内仍缺乏此类轴承性能检测的相关设备。

1—保持架；2—滚动体；3—轴承座；4—螺栓孔；5—推力杆

2 滚动关节轴承摩擦力矩检测装置

滚动关节轴承摩擦力矩检测装置如图2所示，由三转动并联机构、移动平台、光杠、丝杠、固定平台等部分构成。

1—底座；2—移动平台；3—右立柱；4—上压板；5—滚动关节轴承；6—凸缘；7—三转动并联机构；8—左立柱图2 摩擦力矩检测装置机械结构图Fig.2 Mechanical structure diagram of friction torque measuring device

滚动关节轴承通过轴承座上的螺栓孔与并联机构运动平台相连，推力杆通过末端螺纹与凸缘相连，凸缘与上压板连接，并联机构通过球面副与移动平台铰接。立柱支承移动平台，通过调整立柱高度向轴承施加不同的预紧力，等同于拉压试验机。

滚动关节轴承摩擦力矩检测装置的机构原理如图3所示，待检测轴承的推力杆通过凸缘与上固定平台相连，移动副调整移动平台高度至合适位置，轴承座与并联机构运动平台固定连接。三转动并联机构驱动支链运动，带动滚动关节轴承任意方向转动。摩擦力矩检测完成后，将轴承从检测设备中取下。

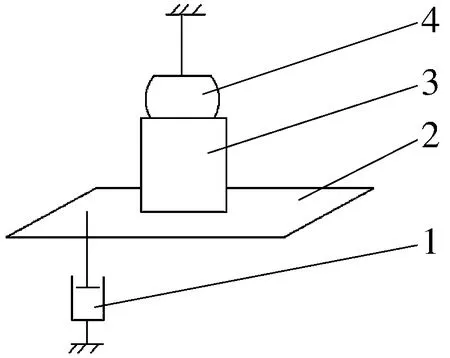
1—移动副；2—移动平台；3—三转动并联机构；4—滚动关节轴承

3 三转动并联机构设计与分析

三转动并联机构是检测装置的核心单元，其构型取决于各支链结构，支链的运动螺旋和约束螺旋则决定着运动平台的自由度。运动平台具有三转动自由度，需要支链限制其3个移动自由度，且具有3个驱动支链。因此，选用SRRR结构为驱动支链，其中S为球面副，R为转动副。如图4所示，支链S1处为S副，与地面相连；A1，B1，R1处为3个R副，其转动轴线平行。

图4 SRRR支链结构Fig.4 Structure of SRRR-limb

在S副处建立笛卡尔坐标系，支链的运动螺旋为

(1)

支链的约束螺旋为

(2)

式中：L1,L2,M1,M2为非零实数。

支链提供一个约束运动平台沿z方向的移动自由度。选取同样的3条SRRR支链，运动平台丧失1个移动自由度；增加1条从动支链，该支链只有1个位于运动平台几何中心的S副，设计的并联机构为3-SRRR/S，如图5所示。

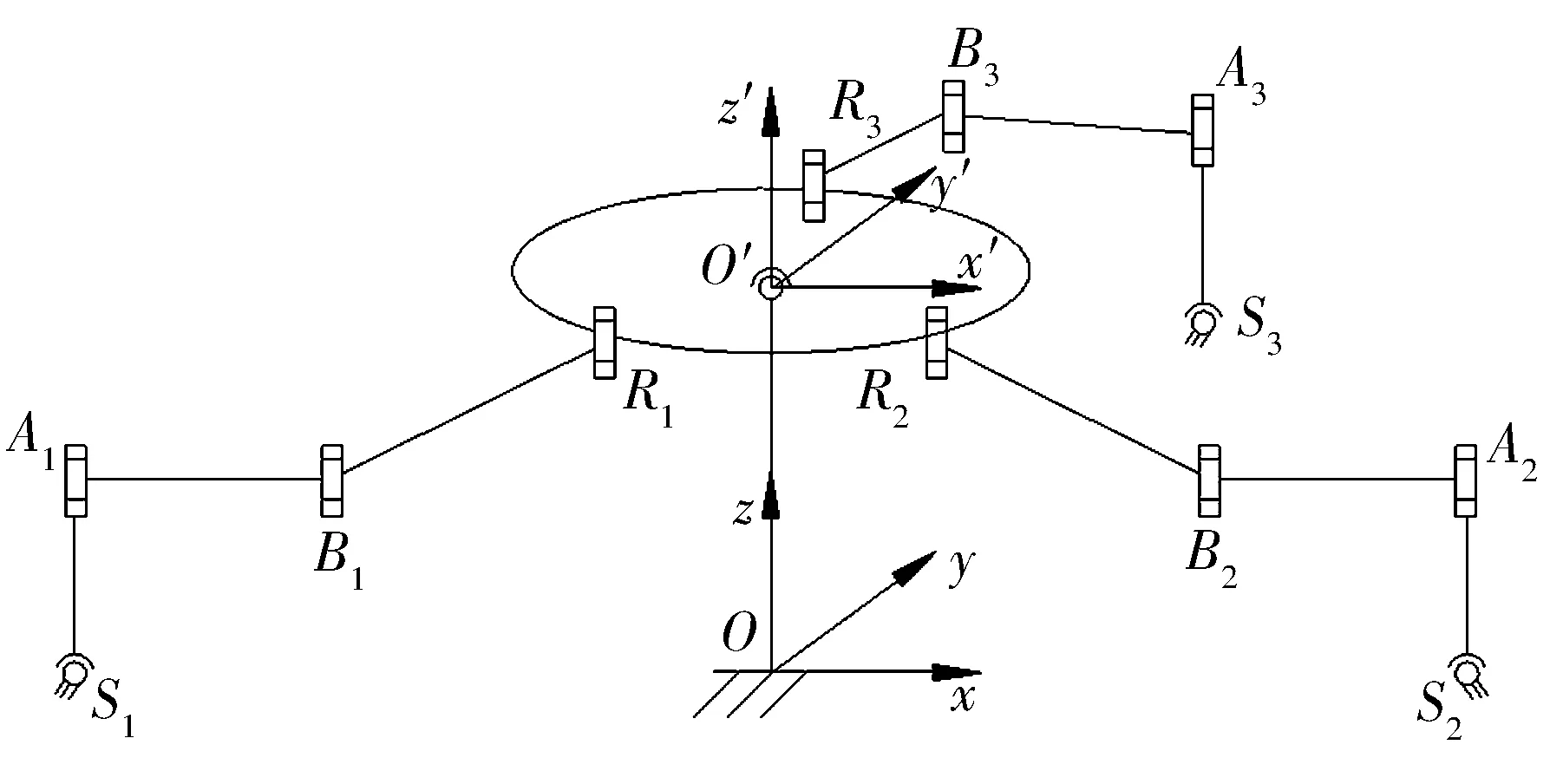
图5 3-SRRR/S并联机构Fig.5 Parallel mechanism of 3-SRRR/S

3-SRRR/S并联机构中，S1，S2，S3与检测装置移动平台相连，待检测轴承的轴承座与运动平台上的螺纹孔相连。显然，由于仅存在1个S副，从动支链具有空间3个转动自由度运动螺旋，3个约束移动的反螺旋。

机构各支链均约束平台沿z轴的移动自由度，存在一个公共约束，因此机构阶数降为5；SiAi(i=1,2,3)构件可以绕自身旋转，为局部自由度。根据修正的Kutzbach-Grübler公式，机构的自由度为

5×(11-13-1)+21-3=3，

(3)

式中：F为机构的自由度数；λ为机构的阶数；n为构件数；g为运动副数；fi为第i个运动副的自由度数；ν为去除公共约束后的冗余约束数(机构中不存在)；ζ为机构中存在的局部自由度数。

综上所述，机构运动平台可以实现空间三转动自由度。

4 机构运动学建模

4.1 位置关系分析

根据图5所示并联机构，以S1A1B1R1驱动支链为分析对象，在△A1B1R1中定义

θ1=∠A1B1R1，

(4)

根据余弦定理可得

(5)

绞点S1与R1之间的距离记为l1，根据支链几何关系和机构学原理可得

(6)

同理，其余2条驱动支链也存在上述几何关系，则

。(7)

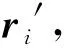
(8)

T=TzTyTx，

(9)

式中：P为动平台中心点矢量，即O′x′y′z′坐标系在Oxyz坐标系下的位置矢量；Tx，Ty，Tz为旋转变换矩阵；α，β，γ分别为滚动(Roll)、俯仰(Pitch)、偏转(Yaw)角的RPY角表示。

li(i=1,2,3)在Oxyz坐标系下的矢量可以表示为

li=ri-Si，

(10)

式中：Si为与地面连接的球面副在Oxyz坐标系下的位置矢量。

(11)

机构的输入参数为θi，输出参数为运动平台姿态角α，β,γ。通过(7)式和(11)式即可得到机构的输入、输出位姿关系。

4.2 速度关系方程

将(7)式对时间求导可得

(12)

机构速度逆雅可比矩阵Jinv为

将(11)式对时间求导可得

(13)

机构速度正雅可比矩阵Jdir为

根据(12)式和(13)式可以得到机构输入角与姿态角变化率之间的关系。运动平台角速度与姿态角和姿态角变化率满足

(14)

式中：ωx，ωy，ωz为Oxyz坐标系下运动平台绕x轴、y轴和z轴转动的角速度。

4.3 加速度关系方程

将(12)式对时间求导可得

(15)

将(13)式对时间求导可得

(16)

将(14)式对时间求导，可得机构运动平台角加速度为

(17)

5 三转动并联机构尺度参数设计与数值算例

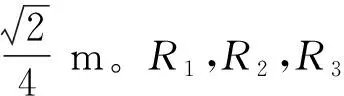
5.1 工作空间分析

运动平台姿态角受O′处S副运动范围的限制，约束条件为[19]

(18)

驱动支链Si处S副的约束条件为[20]

(19)

式中：φ1，φ2，φ3分别为S1，S2，S3处运动副的倾斜角。

除Bi外，机构中的R副可以不约束转动角度。Bi为驱动副，控制θi的角度变化。受杆长和干涉条件限制，θi的约束条件为

(20)

α-β和α-γ姿态角的工作空间如图6所示，计算结果显示，姿态角工作空间呈球面状，运动平台工作空间连续，内部无空洞。

图6 工作空间截面图Fig.6 Cross section of workspace

5.2 位置正解分析

机构输入、输出参数关系表达式为强耦合非线性方程组，可采用粒子群优化算法(PSO)处理此类高维非线性问题[21]。前期采用较大的权重因子w有利于提高算法的探索能力以得到合适的种子，后期采用较小的w则倾向于局部搜索[22-23]。因此，提出一种动态变权重的PSO算法，w的动态变化值定义为

(21)

式中：wmin为最小权重因子，一般为[0.2,0.5]；wmax为最大权重因子，一般为[0.8,1]；kmax为最大迭代次数；k为当前迭代次数。

在工作空间内，将输入θi代入(7)式得到li，建立适应度评价函数为

ffitness(α,β,γ)=

(22)

改进PSO算法求得min{ffitness(α,β,γ)}时的X=(αβγ)T即为位置正解初值，再用拟牛顿(Broyden)法进行迭代计算[24]，结果作为位置正解终值。算法的计算区间为整个工作空间，在工作空间内选取10组姿态角进行对比，结果见表1。

表1 姿态角计算结果Tab.1 Calculation results of attitude angle rad

经过多次计算可知，改进PSO算法受随机初始粒子的影响会使优化结果有所波动，经过一次Broyden迭代计算后精度大大提高，迭代不超过5次即可收敛。

5.3 摩擦力矩测量路径运动学参数计算

模拟轴承任一运动路径，并联机构运动平台中心点从姿态X0(0.034 907，-0.122 17，-0.157 08)T转动到姿态Xf(0.087 266，-0.087 27，-0.104 72)T，单位为rad。要求运动时间为5 s，运动平台初始时刻和终止时刻的角速度和角加速度均为零，采用五次多项式轨迹，运动方程为

X=s0+s1t+s2t2+s3t3+s4t4+s5t5，

(23)

用X表示(αβγ)T，则

(24)

根据X0到Xf姿态的轨迹条件，运动平台姿态角变化方程为

(25

将(25)式代入(11)式得到li的变化曲线，根据(7)式推导可得

(26)

将li计算结果代入(26)式可以得到输入角的变化规律，根据已推导出的运动学关系可得输入角角速度和角加速度的变化规律，如图7所示。运动平台姿态角变化过程中，机构输入角满足工作空间约束条件，角速度和角加速度曲线初始时刻和终止时刻为0，曲线变化平稳。

图7 转动运动发生器运动学参数变化曲线Fig.7 Variation curve of kinematic parameters of rotational motion generator

6 结束语

1)设计了用于滚动关节轴承摩擦力矩测量的混联机构，机构包括实现一个独立运动的移动平台和实现三转动自由度的新型并联机构。

2)建立了三转动并联机构的输入、输出运动学模型，计算了机构运动平台工作空间和位置正解，随机选取一条摩擦力矩检测路径得到了机构运动学参数的变化规律。

3)机构分析计算结果为摩擦力矩检测系统控制策略研究和软件开发奠定了理论基础。

除用于轴承摩擦力矩测量外，该装置也可以用于旋转精度等轴承性能指标的测量。工业生产对设备精度要求越来越高，能耗要求越来越低，滚动关节轴承可以在大幅度空间灵活转动，且能量损失明显小于滑动关节轴承，开发相应的测量设备保证产品质量和使用性能有显著意义。