基于二维图像和自适配归一化SGAN网络的滚动轴承故障诊断
2021-07-22杨青张继云吴东升刘伊鹏
杨青,张继云,吴东升,刘伊鹏
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
滚动轴承作为转子系统的核心部件,被广泛应用于装备制造、精密仪器工程、医疗器械等领域,轴承故障将会引发一系列连锁故障,造成巨大损失[1-2],轴承故障诊断具有重大研究价值。
目前,轴承故障诊断方法可分为4类:基于数学模型、基于数据驱动、基于人工智能、集合型故障诊断方法[3-6]。集合型故障诊断方法融合了单一方法的优点,又可分为基于浅层学习和基于深度学习的集合方法。近年来,基于深度学习的集合型故障诊断方法成为研究重点,如VMD-DBN[7],VMD-LMD-CNN[8],CRN-DBN-DAE[9]等,但对于深度学习而言,数据集质量和标签数量对网络训练起着决定性的作用,需要采集大量特征明显且带标签的数据集。然而在实际工作中,采集的轴承数据都是一维时域信号,特征不明显且不带标签,需要耗费时间和人力对数据进行标注,通常采用半监督学习算法进行处理。
生成对抗网络(Generation Adversarial Networks,GAN)[10]具有学习原始样本的数据分布特征,生成与原始样本逼真新样本的能力。文献[11]提出一种基于辅助分类器生成对抗网络的方法生成逼真的一维信号,文献[12]提出WGAN-CNN方法对故障数据的频谱信号进行过采样以扩充数据集,文献[13]将一维信号转换为频谱信号以解决数据不平衡问题,并提出了FFT-GAN-SDAE的故障诊断方法。
在生成对抗网络的基础上演变出了深度卷积生成对抗网络[14],进一步用softmax代替分类器并修改损失函数后得到了半监督生成对抗网络(Semi-Supervised Generation Adversarial Networks,SGAN)[15]。文献[16]将SGAN与剩余网络结合用于钢表面故障检测,文献[17]提出一种基于自适配归一化半监督生成对抗网络的新型轴承故障诊断方法,文献[18]提出一种联合训练的半监督学习的目标识别方法。
为进一步提高半监督生成对抗网络的故障诊断性能,提出一种VMD-2D-SN-SGAN集合型故障诊断方法:首先将一维的振动信号经过变分模态分解(Variational Mode Decomposition,VMD)降噪后转换为2D图像作为SGAN网络的输入;其次,使用自适配归一化 (Switchable Normalization,SN)替换SGAN网络中的批归一化(BN),防止过拟合并提升网络的泛化能力;然后,利用生成器网络生成轴承图像并与真实图像一起输入到判别器网络中,由softmax输出故障类别并在不同标签比例下优化更新网络参数;最后,将训练好的判别器网络用于二维图像分类。
1 理论分析
1.1 GAN与SGAN
1.1.1 GAN
生成对抗网络由一个生成器网络(G)和一个判别器网络(D)组成,对于给定的训练数据集,生成器网络的目的是生成与训练数据集相似的数据集,判别器网络是一个常见的二进制分类器,主要目的是确定输入的数据是来自真实的数据还是来自生成器生成的数据,并引导生成器网络通过反向传播梯度产生更真实的样本。生成器和判别器的训练过程是一个二元极小极大博弈问题,其目标函数为
Ez~pz(z)[log(1-D2(G(z)))],
(1)
训练过程中,E表示数学期望,应最大化鉴别器的区分度log(D1(x))+log(1-D2(G(z))),最小化生成器和真实数据集的数据分布log(D2(z)),使训练最终达到“纳什均衡”。
生成对抗网络如图1所示,在生成对抗网络中,由判别器学习到的特征可以提升分类器(C)的效果,好的分类器也可以优化判别器的最终效果,生成器的效果也会随判别器效果的提升变得更好,三者会在一个交替过程中趋向一个理想的平衡点。

图1 生成对抗网络流程图Fig.1 Flow chart of GAN
1.1.2 SGAN
传统生成对抗网络的分类器和判别器无法同时训练,因此,为同时训练生成器与分类器,实现一个更优的半监督式分类器(S)并提高生成样本的质量,提出了半监督生成对抗网络。
对于一个N类的分类问题,半监督生成对抗网络采用softmax分类器将输出类别扩展为N+1维,对生成的样本定义额外类别标签引导训练,采用半监督训练损失的方式来训练网络。半监督生成对抗网络的结构如图2所示。

图2 半监督生成对抗网络结构图Fig.2 Structure diagram of SGAN
softmax函数用于N分类神经网络的输出,将每一类的概率压缩在0与1之间,再除以输出总和最终输出一个维逻辑向量{L1,L2,…,LN},从而精确地表示每一类的输入概率,其表达式为
(2)
1.1.3 改进的半监督生成对抗网络

(3)

与其他归一化方法不同,自适配归一化在计算μ和σ2时,从3种归一化方法(批归一化BN、实例归一化IN、层归一化LN)的集合Ω={BN,IN,LN}中选择合适的归一化方法进行加权平均,即
(4)
(5)
式中:Ik为像素值;|Ik|为像素的数量,k∈Ω。
权重系数ωk则利用softmax函数对3个维度的控制参数λk进行计算,即
(6)

自适配归一化在训练期间为每一层网络自动寻找合适的归一化操作,相较于其他归一化方法更易使网络达到最优性能。
1.2 VMD-2D去噪图像化
由于实际采集到的轴承信号为一维时域振动信号,特征不明显并伴随大量噪声干扰,特征提取较为困难,而且卷积神经网络直接处理一维振动信号的效果也不佳。因此,将一维振动信号进行变分模态分解[19]降噪处理,将其转换为2D灰度图像。变分模态分解的原理是将带有噪声的信号分解为频率不同的一系列固有模态分量(IMF),分解模型为
(7)
式中:ωk为中心频率;x为输入信号;uk为k个IMF分量。为约束上述变分问题,采用增广拉格朗日函数计算求约束变分问题的最优解,交替更新ωk和uk,即
(8)
(9)
分解完成后,通过计算相关系数来反映不同变量之间的相关程度。以不同变量与其平均值的差为基准,将差值相乘以表达变量之间的相关程度,计算公式为
(10)
式中:μx,μy分别为原始信号和IMF分量的均值;σx,σy分别为原始信号和IMF分量的标准差。由于噪声信号的频谱能量较低,可将IMF分量与原信号频谱能量的比值ρ0作为阈值来确定相关性。除去相关系数ρxy小于ρ0的IMF分量,将剩余的IMF分量进行重构以达到降噪的目的。经试验对比,设定k=4作为模态分解的数量,设定阈值ρ0=0.3。降噪后将一维信号转换为二维图像,转换过程如图3所示。

图3 VMD-2D变换示意图Fig.3 Transformation diagram of VMD-2D
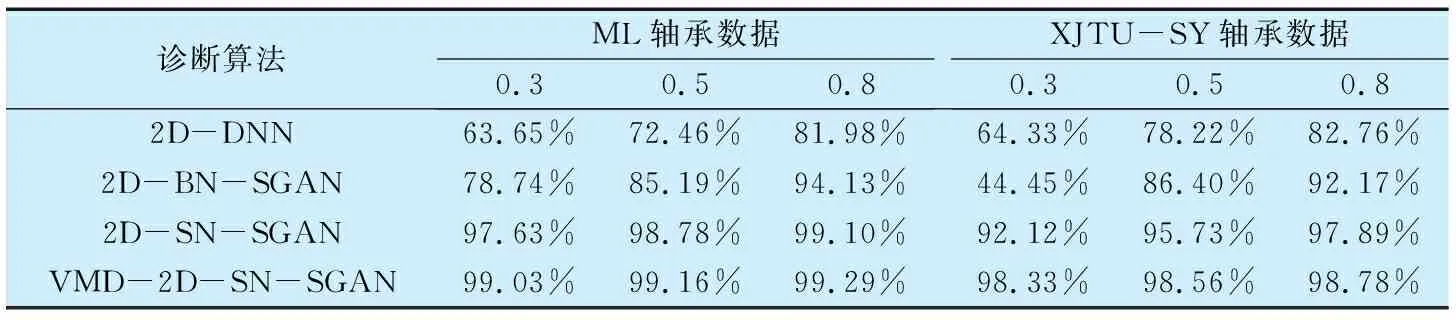
设需要转换图像的像素为N×N,图像对应像素点h,w的值为P[h,w],且1 通过(11)式将振动信号的值V归一化至[0,255]之间,将每个样本归一化的值由取整函数f取整后与图像中像素的强度一一对应,最终二维图像的像素数等于时域信号的个数。 (11) 半监督生成对抗网络的训练实质上是对损失函数的优化过程,softmax分类器先将生成器网络生成的图像样本添加到数据库中,用新的标签y=N+1标注;判别器网络将生成的样本作为输入,由(12)式输出一个N+1维的逻辑向量{L1,L2,…,LN+1}。 (12) 整个网络的损失包括生成器和判别器的损失,其中判别器损失为 LD=Lunsupervised+Lsupervised, (13) Lunsupervised=Lg+Lunlabel, (14) Lg=-Ex~g[logPmodel(y=N+1|x)], (15) Lunlabel=-Ex~pdata[log(1-Pmodel(y=N+1|x)], (16) 式中:Lsupervised为监督损失;Lunsupervised为无监督损失;Lg为生成样本损失;Lunlabel为无标签损失;Pmodel(y=N+1|x)为将样本判断为生成样本的概率。 对于无监督学习部分,判别器只需要输出真假,不需确定类别。生成样本损失就是将生成器生成的图像样本误判为真实样本,用X~g表示取自生成样本,训练中应最小化该损失。无标签损失就是将真实不带标签的样本误判为生成器生成的样本,用1-Pmodel(y=N+1|x)表示将无标签样本判断为真实样本的概率,用x~pdata表示取自真实样本,训练时也应该最小化该损失。 在监督学习部分,半监督生成对抗网络通过最小化真实数据标签与预测分布Pmodel(y|x)之间的交叉熵进行训练,有标签损失为 Llable=-Ex,y~pdata[logPmodel(y|x,y (17) 为实现生成器最大化拟合真实数据的分布,生成更高质量的样本,采用生成器生成与真实数据统计分布相匹配的特征匹配方法,则生成器的损失为 Ex~glog[1-pmodel(y=N+1|x)]。 (18) 基于VMD-2D-SN-SGAN的故障诊断方法总体架构如图4 所示,整个过程包括监督学习和无监督学习:在监督学习部分,真实带标签的数据输入判别器网络,经过卷积、归一化等操作学习标签数据的潜在特征,最后由softmax输出N维概率向量值;在无监督学习部分,生成器网络生成的图像和真实不带标签的图像一起输入到判别器网络,同样由softmax输出二维概率向量值;判别器网络和生成器网络交替训练,优化更新网络参数。 图4 VMD-2D-SN-SGAN的总体架构Fig.4 Overall frame of VMD-2D-SN-SGAN 2.1.1 生成器网络 生成器网络的结构参数见表1,其由4个分数步长卷积层和1个全连接层组成。首先,将符合高斯分布的随机100维噪声向量输入到全连接层,通过维度变换后由分数步长卷积分解输入矩阵;在反卷积后进行自适配归一化处理,前3个反卷积层采用ReLu作为激活函数,最后一个采用Tanh作为激活函数,在激活函数之后加入dropout算法;最终输出一张分辨率为28×28的灰度图像。 表1 生成器网络结构参数Tab.1 Structure parameters of generator network 2.1.2 判别器网络 判别器网络的结构参数见表2,其由4个卷积层和1个全连接层组成。输入尺寸为[B,28,28,1]的图像样本,在卷积操作后进行自适配归一化处理,卷积层均采用LReLu作为激活函数,激活函数之后加入dropout算法,由softmax输出分类结果。 表2 判别器网络结构参数Tab.2 Structure parameters of discriminator network VMD-2D-SN-SGAN方法采用半监督训练方式,共同调整生成器和判别器的损失(均采用Adam优化)使总损失最小,进一步提高故障诊断能力。该方法(图5)的具体步骤为: 图5 VMD-2D-SN-SGAN算法流程图Fig.5 Flow chart of VMD-2D-SN-SGAN algorithm 1)对轴承振动信号进行变分模态分解降噪。 2)将降噪后的信号转为二维灰度图像,按3∶1∶1划分训练集、验证集和测试集。 3)选取符合高斯分布的随机噪声向量输入生成器网络,生成灰度图像。 4)将有标签图像、无标签图像和生成图像按batch-size输入判别器网络中得到分类结果。 5)计算生成器网络和判别器网络的损失。 6)固定生成器网络的参数,采用Adam算法提升随机梯度,优化判别器的权重参数。 7)固定判别器网络的参数,选取全连接层输出作为中间层特征,采用Adam算法降低随机梯度,更新生成器的权重参数。 8)重复第3—7步,直至达到迭代次数。 9)保存模型,将测试图像输入判别器网络,输出故障类别。 数据分析在32G内存,NVIDIA GeForce GTX 1080Ti CPU,Intel i7-8700 3.2GHz 6核12线程的工作站上进行。训练半监督生成对抗网络时,Adam优化算法的学习率(learning rate)设为0.000 1,动量(momentum)设为0.5,dropout rate设为0.5,batch-size设置为16,迭代次数(epoch)设为1 000。试验数据按3∶1∶1划分训练集、验证集和测试集,其中测试集是从整个数据集中随机抽取20%,生成数据与真实数据的比例为1∶1。 采用美国西储大学(CWRU)公开发布的轴承数据[20],选取1 772 r/min工况下的驱动端轴承数据,采样频率为12 kHz,将正常轴承(Health)和钢球故障(B007,B014,B021)、内圈故障(IR007,IR014,IR021)、外圈故障(OR007,OR014,OR021)共10种数据作为研究对象,其中007,014,021分别对应于0.178,0.356,0.534 mm的故障尺寸。每种数据取120 736个采样点进行变分模态分解降噪,降噪完成后每隔784个点生成一张像素为28×28的二维灰度图像,每类故障生成154张图像,所有类别共计1 540张,每类数据生成的灰度图像如图6所示。 图6 CWRU灰度图像Fig.6 Gray images of CWRU 将预处理完成的10类灰度图像输入不同故障诊断模型,在不同标签比例下开始训练,迭代1 000次后的分类结果如图7所示,由图可知:1)2D-SN-SGAN标签比例为0.3时的分类精度达到了92.45%,远远超过2D-BN-SGAN标签比例为0.8时的分类精度,说明2D-SN-SGAN算法虽然收敛速度较慢,但有效解决了过拟合的问题,并提高了分类精度,有更强的归一化能力;2)当标签比例为0.5时,2D-SN-SGAN算法的分类精度上升到93.09%,与标签比例为0.8时相差不大,说明2D-SN-SGAN方法降低了对标签的依赖;3)VMD-2D-SN-SGAN算法在标签比例为0.3时分类精度达到93.05%,当标签比例上升到0.5和0.8时,分类精度分别达到93.13%和94.51%,分类精度和速度均得到了提升,具有更好的性能。 图7 CWRU不同标签比例下的分类精度Fig.7 Classification accuracy of CWRU under different label proportions 与传统机器学习算法FFT-SVM[17]、监督学习算法2D-DNN、半监督方法2D-BN-SGAN及2D-SN-SGAN的分类精度进行对比分析,结果见表3:标签比例对监督学习算法2D-DNN和归一化能力较差的2D-BN-SGAN算法影响较大,对2D-SN-SGAN算法的影响较小,对VMD-2D-SN-SGAN算法的影响不明显。实际中对数据进行大规模标签处理比较困难,而VMD-2D-SN-SGAN算法能够消除标签比例减小带来的影响,实用性得到了显著提高。 表3 CWRU不同标签比例的分类精度Tab.3 Classification accuracy of CWRU with different label proportions 为探索不同batch-size和噪声干扰对网络性能的影响,本章在标签比例为0.5,batch-size分别为4,16,25,64的情况下,对2D-BN-SGAN,2D-SN-SGAN和VMD-2D-SN-SGAN的分类精度进行对比,结果见表4:在同等情况下,小批次对2D-BN-SGAN算法的影响很大,对2D-SN-SGAN和VMD-2D-SN-SGAN算法的影响较小,说明SN在各种批次设置下分类精度都保持稳定,其为不同归一化层选择不同的操作,拓展了归一化技术的边界,弥补其他归一化方法的缺陷;加入VMD则可以增强模型的抗干扰能力,提高分类精度。 表4 CWRU不同batch-size的分类精度Tab.4 Classification accuracy of CWRU with different batch-size 选取东南大学感应电动机ML轴承数据集[21-22]和西安交通大学的XJTU-SY轴承数据集[23-25]作为研究对象。其中,ML轴承数据选取自转频20 Hz,负载配置为2的工况,每类数据取1 019 200个采样点进行VMD处理,降噪完成后每隔784个点生成一张像素为28×28的二维灰度图像,每类故障生成1 300张图像。XJTU-SY 轴承数据选取自转速2 250 r/min,径向力11 kN的工况,每类数据取588 000个采样点进行VMD降噪后每隔784个点生成一张像素为28×28的二维灰度图像,每类故障生成750张图像。 不同标签比例(batch-size为16),不同batch-size(标签比例为0.5)下的分类精度分别见表5、表6,由表可知:VMD-2D-SN-SGAN算法在噪声环境和不同批次设置下均能得到较高的分类精度。说明该模型有较强的泛化能力和鲁棒性,适用于不同的对象以及复杂的环境。 表5 不同标签比例下各算法的分类精度Tab.5 Classification accuracy of each algorithm under different label proportions 表6 不同batch-size下各算法的分类精度Tab.6 Classification accuracy of each algorithm under different batch-size 通过对3组轴承数据集的分析可以发现,由于CWRU轴承数据集的数据量远没有其他2组丰富,VMD-2D-SN-SGAN算法的分类精度不如其他2组高,但在数据量不充足和标记数据稀缺的情况下,依然实现了较高的分类精度和更强的鲁棒性,相比于其他方法更具应用价值。 为提高半监督生成对抗网络的故障诊断精度和泛化能力,提出了一种基于二维图像和自适配归一化半监督生成对抗网络(VMD-2D-SN-SGAN)的集合型故障诊断方法,通过对不同轴承数据集的分析得到以下结论: 1)与监督学习方法、单一型半监督生成对抗网络、其他集合型半监督生成对抗网络相比,在标签样本不足时,VMD-2D-SN-SGAN算法能得到较高的分类精度。 2)面向不同的试验对象,VMD-2D-SN-SGAN算法均能得到更高的分类精度,且具备较强的鲁棒性和泛化能力。 在研究过程中发现,VMD-2D-SN-SGAN算法用于变负载故障诊断时效果有所下降,其在变负载轴承故障诊断方面的应用有待进一步研究。1.3 VMD-2D-SN-SGAN网络训练

2 故障诊断流程
2.1 系统架构



2.2 算法流程

3 试验研究
3.1 分类能力验证




3.2 泛化能力验证

3.3 小结
4 结束语
