基于变分模态分解与灰狼算法优化极限学习机的滚动轴承故障诊断

郑小霞，蒋海生，刘静，魏彦彬

(上海电力大学 自动化工程学院，上海 200090)

滚动轴承作为机械传动系统中的关键部件，运行工况复杂且需持续运行，对机械设备的生产效率和安全有很大影响。因此，准确提取滚动轴承的故障特征信息并识别故障类型，对减少机械设备故障，提高运行效率具有重要意义[1]。

在振动信号分析中，小波分解和经验模态分解(EMD)等已得到广泛应用，但小波阈值及小波基的选取问题，EMD的端点效应和模态混叠问题大大影响了有效特征向量的提取，使得故障特征的提取及处理具有一定的局限性。变分模态分解(Variational Mode Decomposition,VMD)是一种新型非平稳信号自适应分解估计方法[2]，通过交替方向乘子实现对变分模型最优解的迭代搜索，克服了模态混叠和端点效应等缺点，实现了本征模态分量(IMF)的有效分离，适用于处理机械设备振动信号[3]。单隐含层的浅层神经网络——极限学习机(Extreme Learning Machine，ELM)与传统分类方法相比，具有学习速度快,泛化性能好等优点[4]。文献[5]运用局部均值分解与ELM对行星齿轮箱进行故障识别并取得不错效果。文献[6]提出多隐层核极限学习机对滚动轴承进行故障诊断，尽管故障识别准确率有所提升，但训练模型复杂，训练和学习时间大大增加。

针对上述问题，本文提出一种变分模态分解与灰狼算法(Gray Wolf Algorithm，GWO)[7]优化极限学习机相结合的故障诊断方法，通过VMD处理得到一组本征模态分量，计算各模态分量的模糊熵值并输入到改进ELM模型中进行轴承的故障诊断。

1 基于VMD和模糊熵的特征提取

1.1 算法原理

变分模态分解的核心思想是构建和求解变分问题[6]。对于变分问题的构造，假设多分量信号f(t)可分解为k个有限带宽的本征模态分量uk，其中心频率为ωk。对每个分量进行希尔伯特变换，计算解析信号得到其单边频谱，将各分量的频谱通过混频调制到相应的基频带上，即

[(δ(t)+j/(πt))*uk(t)]e-jωkt。

(1)

计算解析信号梯度的L2范数并估计各模态函数的带宽，受约束变分模型可表示为

(2)

式中：{uk}={u1,u2,…,uk}；{ωk}={ω1,ω2,…,ωk}。

对于变分问题的求解，引入二次惩罚因子α和拉格朗日乘子λ，将(1)式转化为非约束变分问题，得到增广拉格朗日表达式

L({uk},{ωk},λ)=

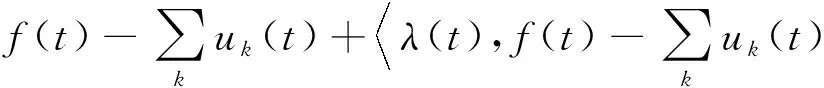
(3)

采用方向交替乘子算法进行求解，从而使uk，ωk和λ不断迭代更新，最后得到(3)式的鞍点，即为模型的最优解。

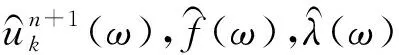
。(4)

振动信号的变分模态分解能够凸显原始信号中多尺度信息的特征，为量化分解后多尺度信息的特征并准确提取振动信号的特征向量，引入模糊熵的概念构建高维特征向量。模糊熵是一种时间序列复杂度的预测方法[8]，其采用均值算法和隶属度函数方法模糊了向量的相似性度量。模糊熵与样本熵等有着相似的理论特性，其优势在于参数变化下的熵值更加稳定。

设x(1),x(2),…,x(N)为各本征模态分量序列，通过(5)式将一维序列转换为m维向量，即

(5)

1.2 关键参数选取

为提取出能够有效反映滚动轴承工作状态的特征向量，需要在变分模态分解与模糊熵计算的过程中选取有效参数。采用美国凯斯西储大学的滚动轴承试验数据进行分析，其中电动机负荷工况为1hp，电动机转速为1 772 r/min，采样频率为12 kHz，试验轴承型号为SKF 6205，故障直径为0.534 mm，选取轴承在正常状态、内圈故障、钢球故障及外圈故障4种工作状态的振动信号。

采用的计算机系统为Window7旗舰版，处理器为AMD A10，内存为8 GB。仿真分析均在MATLAB 2018a中运行。

对振动信号进行变分模态分解时，模态个数K对分解结果的影响很大：当K值较小时，由于变分模态分解算法相当于自适应维纳滤波器组，会造成原始信号中一些重要信息的丢失；当K值较大时，相邻模态分量的频率中心会相距较近，易造成频率混叠。将滚动轴承各工作状态下振动信号在不同K值时的本征模态分量对应的中心频率进行比较，发现模态个数为7时各中心频率较为接近，易在分解时出现模态混叠的现象，因此本文模态个数K取值为6。

1.2.2 模糊熵参数的选取

在计算本征模态分量的模糊熵值时，需考虑3个参数，即时间序列长度N、嵌入维数m和相似容限度r。理论上，较大的m会包含更多的数据信息，但同时要求N或r也足够大；然而，过大的r会导致信息丢失，过小的r则会增加噪声对结果的敏感度，所以一般取r=(0.1～0.5)σstd(σstd为原数据的标准差)。

为确定合适的模糊熵参数，计算不同参数取值时轴承振动信号的模糊熵，结果如图1所示，由图可知：

图1 模糊熵随r,m,N值的变化Fig.1 Variation of fuzzy entropy with values of r，m and N

1)在m=2，N=2 048时，内圈故障与钢球故障的模糊熵值很接近，不易区分。而在r>0.2σstd之后，4种状态下的模糊熵值有明显的区别，可用于故障类型的识别，因此选取r=0.25σstd。

2)在r=0.25σstd时，根据轴承4种工作状态m从2到8的情况所对应模糊熵的变化发现，正常、内圈故障以及钢球故障时模糊熵值曲线随N值变化缓慢下降，没有出现波动现象，但在外圈故障时模糊熵值的变化不稳定；N<1 024时4种工作状态下的模糊熵值存在波动交叉的状态，高维特征向量易出现交叉混叠，导致故障识别误差，因此选取N=2 048。

3)在r=0.25σstd，N=2 048时，嵌入维数m过小会出现4种工作状态模糊熵交叉的情况，影响后续故障诊断的精确度；在m≥3后，4种工作状态下的模糊熵值无交叉现象，因此选取m=3。

2.1 极限学习机

极限学习机的网络训练模型采用单隐层神经网络，设有N个任意样本(xi,yi)，其中xi∈Rm，yi∈Rn，则具有L个隐含层节点的极限学习机模型可表示为

(6)

式中：βj为连接第j个隐层节点与网络输出节点的输出权值向量；g(x)为隐含层神经元的激活函数；

ωj为连接网络输出层节点与第j个隐含层节点的输入权值向量；bj为第j个隐含层节点的偏置；yi为样本的网络输出，yi=[yi1,yi2,…,yin]T。

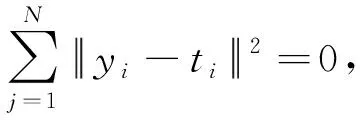
(7)

转化为矩阵形式可得

Hβ=T，

(8)

其中

(9)

此时，输出权值矩阵β=[β1,β2,…,βL]T可表示为

β=H+T，

(10)

式中：H+为隐含层输出矩阵H的Moore-Penrose广义逆矩阵。

2.2 灰狼-极限学习机(GWO-ELM)

极限学习机的训练速度快，泛化性能好，被广泛用于各种设备的故障识别。由于输入层与隐含层之间的输入权值ωj和隐含层偏置bj随机产生且保持不变，因此模型中一些隐含层节点的权值和偏置对数据训练的作用小，进而影响到训练速度和分类准确度。为提高模型性能，本文引入灰狼优化算法对极限学习机中的ωj，bj进行优化，所建立的模型如图2所示。

图2 GWO-ELM模型图Fig.2 Diagram of GWO-ELM model

3 仿真分析

仿真分析采用凯斯西储大学的滚动轴承试验数据，包括电动机在0hp(1 797 r/min)，1hp(1 772 r/min)，2hp(1 750 r/min)和3hp(1 730 r/min)工况下SKF 6205轴承正常、内圈故障、钢球故障及外圈故障4种状态的振动信号(每个工况下每种状态振动信号各50组，数据长度为2 048)。

经变分模态分解得到一组本征模态分量实现对信号的多尺度化，计算各分量的模糊熵并构建高维特征向量。在每组信号中随机选取25组作为训练集样本，剩余25组作为测试集样本。将训练集数据作为GWO-ELM模型的输入，灰狼种群数为100，ELM的输入层节点数为6，隐含层节点数为10，激活函数为sigmod。

试验结果表明GWO-ELM模型对此类数据的故障识别率可达100%，但考虑到上述轴承数据为实验室环境下采集的标准数据，而在实际工况下采集的滚动轴承振动信号中含有很强的噪声，故在上述轴承数据中分别添加2，4，6，8，10 dB的高斯白噪声作进一步分析，以测试GWO-ELM模型对噪声的鲁棒性。同样，对添加噪声后的信号进行变分模态分解，计算各分量的模糊熵值并构建高维特征向量进行信号特征提取。

添加6 dB高斯白噪声后轴承振动信号各分量的模糊熵如图3所示，由图可知：轴承各工作状态下本征模态分量的模糊熵值层次分明且呈现出一定规律，表明变分模态分解与模糊熵相结合能够有效提取含噪信号的多尺度特征向量。

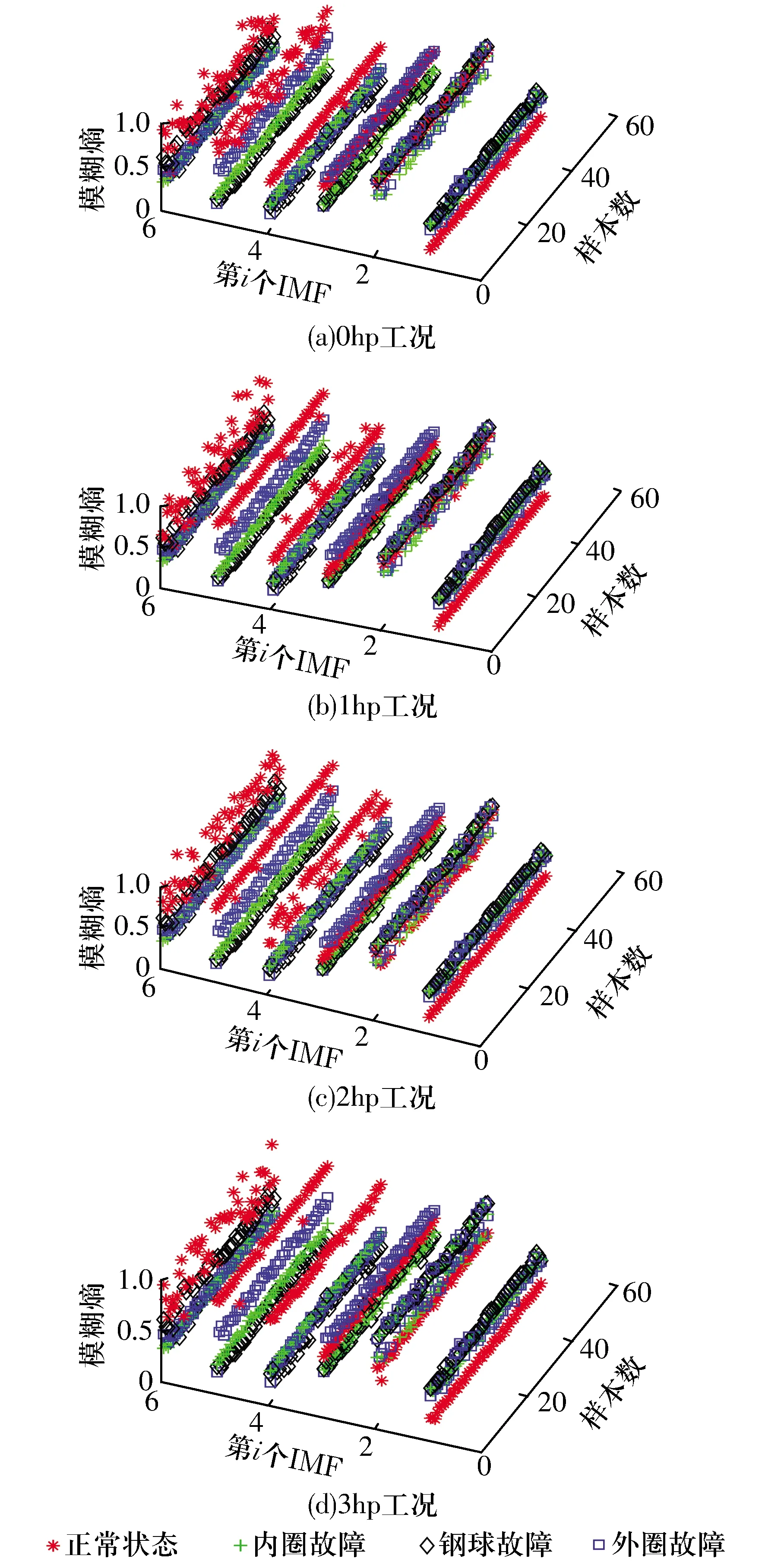
图3 不同工况下轴承振动信号(含6 dB高斯白噪声)本征模态分量的模糊熵Fig.3 Fuzzy entropy of IMF of bearing vibration signals with Gaussian white noise for 6 dB under different operating conditions

在含噪轴承振动信号构建的高维特征向量中，各工作状态下随机选取25组作为训练集样本，剩余25组作为测试集样本，模型参数设置同上。通过适应度函数选择最优的ωj和bj引入到ELM中进行30次仿真试验，添加6 dB噪声轴承振动信号的收敛曲线如图4所示。试验结果表明，GWO-ELM模型收敛速度快，在适应度值达到稳定时，训练集准确率可达98%。

图4 不同工况下的适应度曲线Fig.4 Fitness curves under different operating conditions

将测试集样本数据输入到训练好的GWO-ELM模型中，采集30次故障诊断结果计算平均准确率，结果见表1，由表可知：添加不同信噪比的高斯白噪声后，不同工况下轴承的分类识别结果仍能保持很高的准确率，并且随着所添加高斯白噪声信噪比的增大，故障识别率呈现出逐渐提高的趋势，说明GWO-ELM模型在轴承含噪情况下的故障诊断上具有一定的鲁棒性与实用性。信噪比为6 dB时故障数据的具体分类识别结果如图5所示，其中标签1,2,3,4分别对应正常、内圈故障、钢球故障、外圈故障，不同工况下的故障识别率分别达到了96%，96%，92%，91%。

图5 不同工况下轴承振动信号(含6 dB高斯白噪声)的故障分类结果Fig.5 Fault classification results of bearing vibration signals with Gaussian white noise for 6 dB under different operating conditions

表1 不同含噪轴承振动信号的故障识别率Tab.1 Fault recognition rate of bearing vibration signals with different noises

4 实际数据分析

为验证GWO-ELM模型在实际滚动轴承故障诊断中的实用性，采用某3 MW海上风电机组滚动轴承数据并与常规极限学习机(ELM)、多隐层极限学习机(M-ELM)进行对比分析。其中，GWO-ELM模型参数设置同上，M-ELM模型隐含层层数设置为3。

由于数据来源所限，选取正常、外圈故障、内圈故障3种状态下的轴承振动信号，每种状态取72组数据，数据长度为2 048。现场轴承故障数据经变分模态分解后所得分量的模糊熵如图6所示，各分量的模糊熵值呈现出一定的规律，表明基于VMD与模糊熵的方法能够有效提取现场轴承故障信号的高维特征向量。

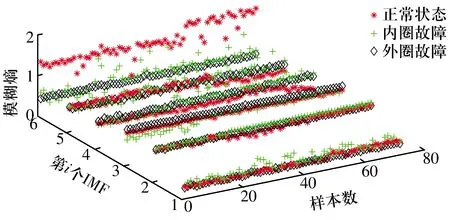
图6 现场轴承振动信号各分量的模糊熵Fig.6 Fuzzy entropy of each IMF of bearing vibration signals on site

在每种状态轴承数据中随机选取36组作为训练集，剩余的36组作为测试集，将训练集样本与测试集样本分别输入GWO-ELM，ELM及M-ELM故障诊断模型进行分析。为避免偶然性，取30次结果的平均值对3种故障诊断模型的故障时间及识别率进行对比，结果见表2。由表2可知：GWO-ELM模型具有最高的识别率，且诊断速度快于M-ELM。这是由于ELM和M-ELM中的ωj和bj均为随机产生，故ELM的识别率较低，而M-ELM经过多次的训练和学习，识别率有所提升，但增加了模型的学习和训练时间，使得故障诊断总时间大大增加。综上分析，相对于ELM和M-ELM，GWO-ELM模型在滚动轴承故障诊断中具有很大优势，更具实用性。

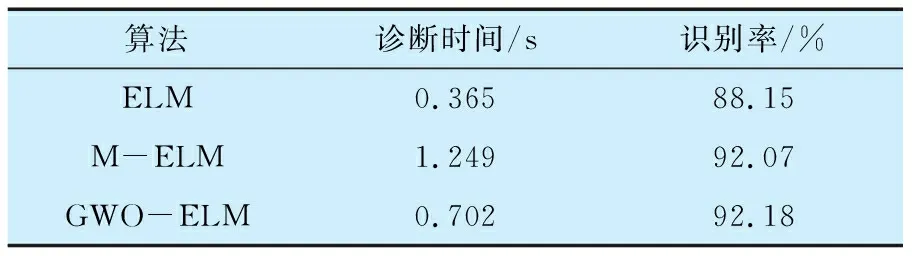
表2 不同故障诊断模型的结果对比Tab.2 Comparison of results among different fault diagnosis models

5 结束语

针对滚动轴承在不同工作状态下的故障诊断问题，提出一种基于变分模态分解和GWO-ELM的故障诊断方法。对西储大学的标准数据添加不同分贝噪声后的故障分类取得了不错的诊断效果，而采用某风电场实际数据进行ELM，M-ELM和本文方法的对比分析，更充分表明GWO-ELM在轴承故障分类中识别率高，速度快，实用性强。